GDP时间序列的ARIMA模型研究

冯 瑞

(重庆工商大学 数学与统计学院，重庆 400067)

ARIMA模型全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average Model)，简记ARIMA，是由博克思(Box)和詹金斯(Jenkins)提出的著名时间序列预测方法，又称为Box-Jenkins模型、博克思-詹金斯法.其中ARIMA(p，d，q)称为差分自回归移动平均模型，AR是自回归，p为自回归项，MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数.所谓ARIMA模型，是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型.ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)以及ARIMA过程[1].

GDP是国民经济核算的核心指标，也是衡量一个国家或地区经济状况和发展水平的重要指标.从价值形态看，它是所有常住单位在一定时期内所生产的全部货物和服务价值超过同期投入的全部非固定资产货物和服务价值的差额，即所有常住单位的增加值之和；从收入形态看，它是所有常住单位在一定时期内所创造并分配给常住单位和非常住单位的初次分配收入之和；从产品形态看，它是最终使用的货物和服务减去进口货物和服务.国内生产总值GDP是核算体系中一个重要的综合性统计指标，也是中国新国民经济核算体系中的核心指标.它反映一国(或地区)的经济实力和市场规模.一个国家或地区的经济究竟处于增长抑或衰退阶段，从这个数字的变化便可以观察到.当GDP的增长数字处于正数时，即显示该地区经济处于扩张阶段；反之，如果处于负数，即表示该地区的经济进入衰退时期了.国内生产总值是指一定时间内所生产的商品与劳务的总量乘以“货币价格”或“市价”而得到的数字，即名义国内生产总值，而名义国内生产总值增长率等于实际国内生产总值增长率与通货膨胀率之和.一般情况，GDP会呈现强烈的趋势特征[2].这些具有趋势特征的经济变量，当发生经济震荡或者冲击后，一般会出现两种情形，一是受到震荡后，经济变量逐渐又回到它们的长期趋势，二是这些经济变量没有回到原有轨迹，而呈现游走状态[3].若研究的经济变量遵从一个非平稳过程，运用最小二乘法理论是不成立的.然而GDP常作为模型的重要变量,许多预测模型依赖于GDP数据,GDP的预测有非常重要的意义.基于以上的原因,许多研究者致力于对GDP的估计.此处用ARIMA模型对全国的GDP进行估计和预测[4],希望对关注中国经济发展的人们有所借鉴.

1 ARIMA(p,d,q)模型建立过程

1.1 数据来源与平稳性检验

通过查阅《中国统计年鉴》,得到1979-2012年，以当年价格表示的国内生产总值(GDP)序列，如表1所示.

1978年我国实行的改革开放政策对国民经济发展产生了至关重要的影响，1979年是改革之后的一年，改革的影响效果更能直接反应到GDP上，所以选择1979-2012年的数据，并对上述数据取对数得到1979-2012年GDP的对数值log(GDP)，画出log(GDP)的趋势如图1.

从图1可以看出，对数GDP曲线呈直线上升的趋势；对数GDP序列具有一定的非线性趋势性.因此从图形可以初步判断该序列是非平稳的.对对数GDP的平稳性进行进一步ADF检验(表2).

从表2中可以看出，在1%，5%，10%3个显著性水平下，单位根检验的临界值分别为-3.679 32，-2.967 77，-2.622 99,T统计量的值为-1.270 35，大于相近临界值，从而无法拒绝原假设,表明对数GDP的差分序列存在单位根.因此,该时间序列是非平稳的时间序列,即使采用传统法拟合直线或指数曲线等趋势模型都存在自相关,预测结果与实际情况存在很大的差距.

表1 1979-2012国民总收入亿元

年份国民总收入年份国民总收入19794 062.579199670 142.4919804 545.624199778 060.8519814 889.461199883 024.2819825 330.451199988 479.1519835 985.552200098 000.4519847 243.7522001108 068.219859 040.7372002119 095.7198610 274.382003134 977198712 050.622004159 453.6198815 036.822005183 617.4198917 000.922006215 904.4199018 718.322007266 422199121 826.22008316 030.3199226 937.282009340 320199335 260.022010399 759.5199448 108.462011468 562.4199559 810.532012516 282.1

为消除时间序列的非平稳性影响，将对数GDP的一阶差分值记为Dlog(GDP)，表3为对数GDP的一阶差分的ADF检验[5].

从表3中可以看出,在1%，5%，10%3个显著性水平下，单位根检验的临界值分别为-3.679 32,-2.967 77,-2.622 99,T统计量的值为-3.656 84，基本小于相近临界值，并且P值小于0.05，从而拒绝原假设,表明对数GDP的差分序列不存在单位根.因此,该时间序列是平稳的时间序列.通过上述的检验表明对数GDP是一阶单整的，即对数GDP的一阶差分DlogGDP～I(1).

表2 对数GDP的ADF检验

表3 对数GDP一阶差分ADF检验

1.2 ARIMA模型p，q值的确立

既然对数GDP的一阶差分是平稳的时间序列,则阶数d=1，现在确定ARIMA(p，d，q)中的p，q值，利用Eviews画出对数GDP的自相关图(图2)：

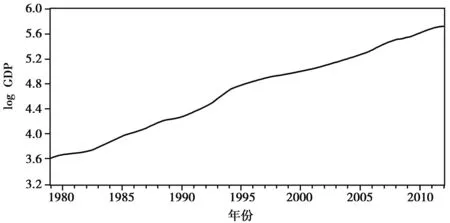
图1 log(GDP)的趋势图

图2 对数GDP的自相关函数图

从图2中可以看到，对数GDP的自相关图形与偏相关图形均呈现拖尾的势态(从图形上看,自相关与偏自相关的波动逐渐减小并没有突然收敛到临界值水平范围内;从数值上看,自相关与偏自相关的数值慢慢减少)，观察自相关与偏自相关的波动图形可知对数GDP的自相关函数一阶都是显著的(超过图中虚线部分)，并且从第二阶开始下降，数值也不太显著，因此先设定q值为1.对数GDP的偏自相关函数也是一至四阶都较显著，从第五阶开始下降很大，此后一直收敛在临界值水平范围内.因此先设定p的值为1～4.因为是一阶差分所以d取1.

模型参数估计一般分两步进行,首先找出参数的初步估计,又称矩估计,然后在初步估计的基础上,根据一定准则,求得参数在某种意义下的精确估计.通常用尤利-沃克方程作参数的矩估计,用最小二乘法和极大似然估计法作参数的精确估计.

表4 不同p、q取值下的ARIMA模型

由重新拟合的时间序列方程，可以看出AIC统计量数值为-4.985 13，较低，ARIMA(p，d，q)在p取0，q取1的时候较优，而且方程的T统计量也通过检验，可决系数R也基本满足要求，现进行白噪声检验，对残差进行白噪声检验(图3).

由图3可知，Q统计量的P值均是大于0.05的，所以时间序列残差项通过白噪声检验，因此最终建立的模型是ARIMA(0,1,1).对数GDP的ARIMA模型如下：

Dlog GDP=0.063 573 429 782 3+εt-0.769 158 166 187*εt-1

1.3 ARIMA模型预测

通过模型进行预测,用Eviews测算出评价预测的一些标准，如表5所示.可以看到，希尔不相等系数为0.19，表明模型的预测能力比较好，而它的方差比例较大，说明实际序列的波动较大，而模拟序列的波动较小，这可能是由于预测时间过长.

通过模型预测，预计2013年GDP为550 404.4亿元，2013年实际GDP为568 845.21亿元，相差3.24%，误差较小，模型拟合较好.

图3 残差白噪声检验

表5 ARIMA模型预测效果

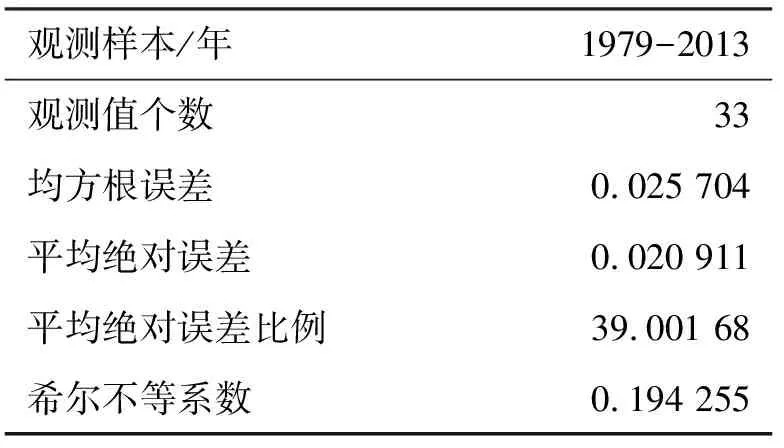
观测样本/年1979-2013观测值个数33均方根误差0.025 704平均绝对误差0.020 911平均绝对误差比例39.001 68希尔不等系数0.194 255

2 结 语

经典计量经济学建模过程中，通常假定经济时间序列是平稳的，而且主要以某种经济理论或对某种经济行为的认识来来确定计量经济学的模型理论的关系式，借用此形式进行数据收集.然而在经济领域中许多时间序列数据不是由平稳过程产生的，此处研究的国内生产总值GDP随时间的位移而持续增长，由于在实际中遇到的时间序列数据很可能是非平稳序列，而平稳性在计量经济学建模中又具有重要的地位，因此此处对对数GDP时间序列进行了单位根检验，确定了模型的平稳性，得到了对数GDP的差分阶数，由此建立了ARIMA模型，并根据对数GDP时间序列的自相关确定了ARIMA中p，q的值，最终得到对数GDP的ARIMA(0,1,1)模型，并对ARIMA(0,1,1)进行了白噪声检验，确定模型残差项的信息已提取完全，证实了模型调整后的平稳性与模型自回归影响的持久性.

参考文献：

[1]龚国勇.ARIMA模型在深圳GDP预测中的应用[J].数学的实践与认识,2008(4):53-57

[2]孙合超.ARMA算法在GDP预测中的应用[J].金田，2013(6):389-390

[3]杨茜.基于ARMA模型对我国GDP季度数据的建模[J].行政事业资产与财务,2011(6):105-106

[4]高铁梅.计量经济分析方法与建模[M].北京：清华大学出版社,2006

[5]靳庭良.DF单位根检验的势及检验式的选择[J].统计与决策,2005(10):13-17