不耐烦顾客强度为高次幂函数的M/M/C/N排队模型

李厚朋， 冀 云， 付馨雨

(重庆师范大学 数学学院，重庆 401331)

1 模型假设

为了方便对多服务窗混合制M/M/C/N模型的研究，在此做以下假设：服务系统中有C个服务窗且系统容量为N(N>C)；各个服务台间是相互独立，且各服务台的服务时间都服从参数为μ的负指数分布；记αk为具有不耐烦顾客离开的概率，αk=knδ,δ≥0，k表示的是等待队长；顾客到达系统的时间间隔服从参数为λ的负指数分布。

2 数学模型

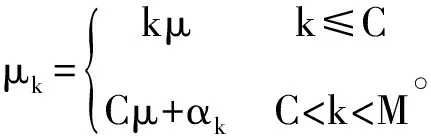
这里αk=knδ(δ>0)，k为排队等待队长。其状态转移如图1所示。

图1 具有不耐烦顾客M/M/C/N 模型状态流图

3 平稳分布

定理设X(t)为t时刻M/M/C/N系统中的顾客数，令

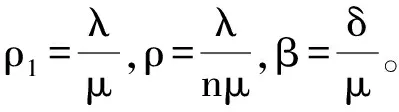
证明：则由上述状态转移图可以列出K氏方程，即：

由0状态

由1状态

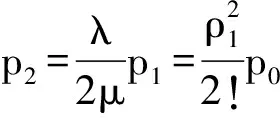
C-1

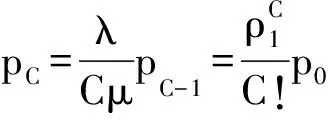
由C状态

λpC=(Cμ+δ)pC+1

⋮

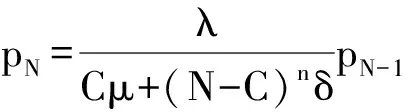
所以

所以有：

4 主要指标

由定理得到出了输入率可变的M/M/C/N排队模型中的转移概率，再由平稳分布便可得到系统主要指标。

系统的损失概率p损：

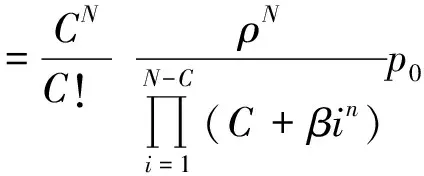
系统的相对通过能力Q：

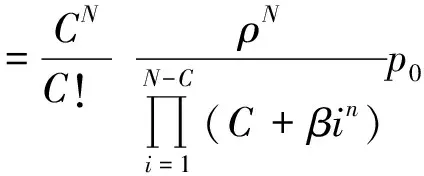
单位时间平均损失顾客人数λ1，平均进入系统的顾客数λe：

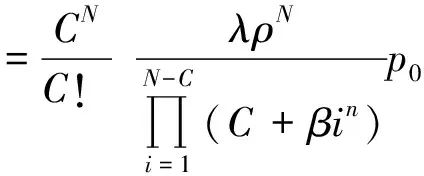
平均排队等待队长：

平均队长：

Ls=Lq+L服=

根据Little公式，可得平均等待时间和可得逗留时间Ws:

5 总 结

本文将讨论不耐烦顾客强度αk=knδ,δ≥0的多服务窗混合制M/M/C/N排队模型。特别地，当本文的参数取特殊值时就能得到文献[1-3]中一系列结论，因此本文是其推广和拓展。

参考文献：

[1] 李焕.具有可变输入率和不耐烦顾客M/M/n的排队模型[J]. 重庆师范大学学报：自然科学版，2011，28(5)：49-52

[2] 台文志，高世泽.一类具有可变输入率的M/M/1排队模型[J].重庆师范大学学报：自然科学版，2009，26(1)：69-73

[3] 邓春华.具有可变输入率的M/M/n排队模型[J].绵阳师范学报，2010(3)：8-10

[4] 谭畅.具有可变输入率的M/M/1排队系统的研究[J].贵州大学学报，2008(9)：51-54

[5] 高世泽. 概率统计引论[M]. 重庆：重庆大学出版社，2000

[6] 唐应辉，唐小我.排队论基础与分析技术[M].北京：科学出版社，2006

[7] 孙荣恒.随机过程及其应用[M].北京：清华大学出版社，2004