自习教室开放的优化管理模型*

王 安 平

(长江大学 工程技术学院，湖北 荆州 434020)

1 问题的提出

近年来，大学用电浪费比较严重，集中体现在学生上晚自习上，一种情况是去某个教室上自习的人比较少，但是教室内的灯却全部打开，第二种情况是晚上自习的总人数比较少，但是开放的教室比较多，这就要求提供一种最节约、最合理的管理方法。

为了培养大学生的节能意识，学校为开放自习室安排了一些相应的制度，使能源浪费最少，但也必须保证同学们正常的上自习，经过与教务处协商学校准备开设四类教室供给同学们上自习，其中前3类教室均匀分布在3个楼层，第四类在3楼。每类教室的具体情况如表1：

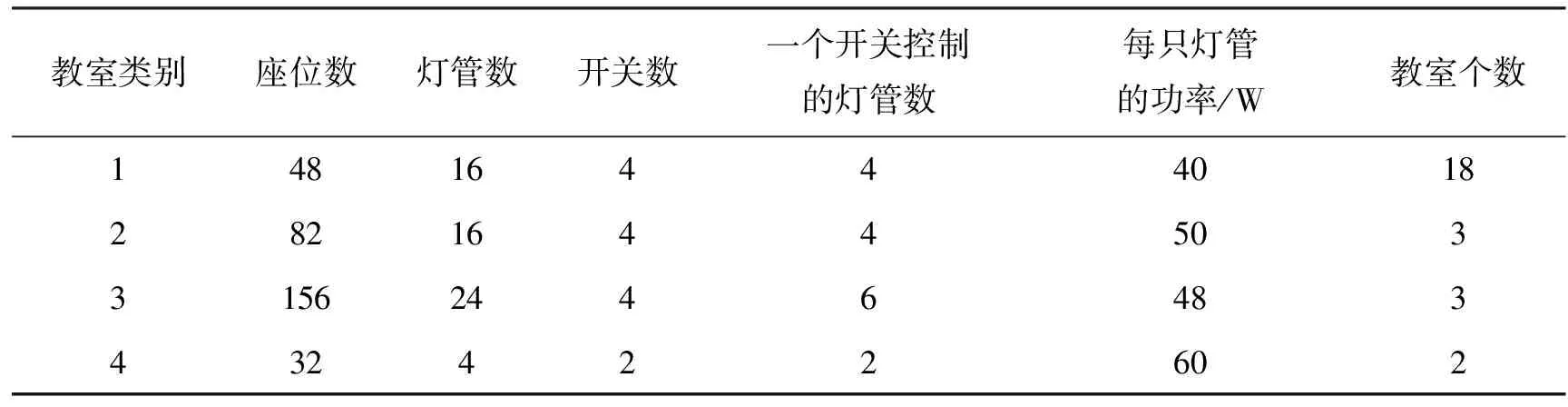
表1 教室的相关数据

根据其条件讨论求解：

管理人员只需要每天晚上开一部分教室供学生上自习，每天晚上从7：00～10：00开放(如果哪个教室被开放，则假设此教室的所有灯管全部打开)，完成以下问题：

(1) 假如我院有1 000名同学，每个同学是否上自习相互独立，上自习的可能性为0.6。要使需要上自习的同学满足程度不低于90%，开放的教室满座率不低于4/5，同时尽量不超过90%。安排哪些教室开放，能达到节约用电的目的。

(2) 假设现有的26个教室分为3个自习区，第一类为第一区，第二类及第四类为第二区，第三类为第三区。教室的开放次序先开放第一区，在开放第二区，最后考虑第三区教室。在满足问题1条件下，教室开放情况又怎样安排。

(3) 假设临近期末，上自习的人数突然增多，每个同学上自习的可能性增大为0.85，要使需要上自习的同学满足程度不低于99%，开放的教室满座率不低于4/5，同时尽量不超过95%。教室如何开放用电最省。

若假设每个教室中每个灯管照亮座位的情况是一致的，开放的教室可以只打开部分灯管，这时的各种情况的教室开放情况怎样调整。

2 问题的假设

假设同学们上自习的概率不受天气的影响，即概率不变；假设灯泡、桌子、椅子都是你好的没有损坏可以给同学们正常使用；假设学校中供电正常，不能造成停电现象；假设灯管与座位分布均匀；假设问题中同学的上自习的概率与自习室的距离无关。

3 符号说明

xi为需要开放第i类教室的个数(i=1，2，3，4)；Z为所有开放教室总的用电量；Wi为第i类教室的耗电量；p为可能上自习的人数；S为开放教室总的座位数。

4 模型的建立与求解

4.1 问题一的建立与求解

建立此模型针对题目的大体思路，运用0-1规划建立最优化模型。教室是否开放：

每间教室的耗电量=灯管数×每只灯管的功率×时间。

第一类：W1=16×40×3=1.92kW·h；第二类：W2=16×50×3=2.4kW·h;第三类：W3=24×48×3=3.456kW·h；第四类：W4=4×60×3=0.72kW·h。

针对问题一建立简单的线性规划模型：

学院有1 000名同学，每个同学是否上自习是独立的，上自习的可能性是0.6，所以可能上自习的人数p=1 000×0.6=600。

要使需要上自习的同学满足程度不低于90%，必须要安排的座位数满足：

48x1+82x2+156x3+32x4≥600×90%

开放的满座率不低于4/5，同时尽量不超过90%，则要满足：

根据题中条件，来分析所需要的目标函数，既要使用电量达到最少，必须满足所给约束条件，再来建立线性规划的模型：

minZ=W1x1W2x2W3x3W4x4

运用LINGO进行编程求解得目标函数Z的最小值为21.84kW·h，相应的开放的教室分别为：第一类教室开放11个；第二类教室开放2个；第三类教室开放0个；第四类教室开放1个。

综上所述，当教室开放个数按类别依次为11、2、0、1时，既满足了同学们的需要，又可以达到节省用电量的目的，即最省用电量为21.84kW·h。

4.2 问题二的建立与求解

问题二将26个教室分为3个区，而没有具体数据进行详细的分析计算来安排教室的开放情况。采用列举法将尽可能开放的教室一一列举出来再分析教室开放的情况，在满足问题一条件下找出能使电量最省的安排情况，要求在先开放第一区，首先考虑有要上自习的同学全部去第一区，然后再去考虑二区的开放情况和三区的开放情况，具体安排如表二所示。

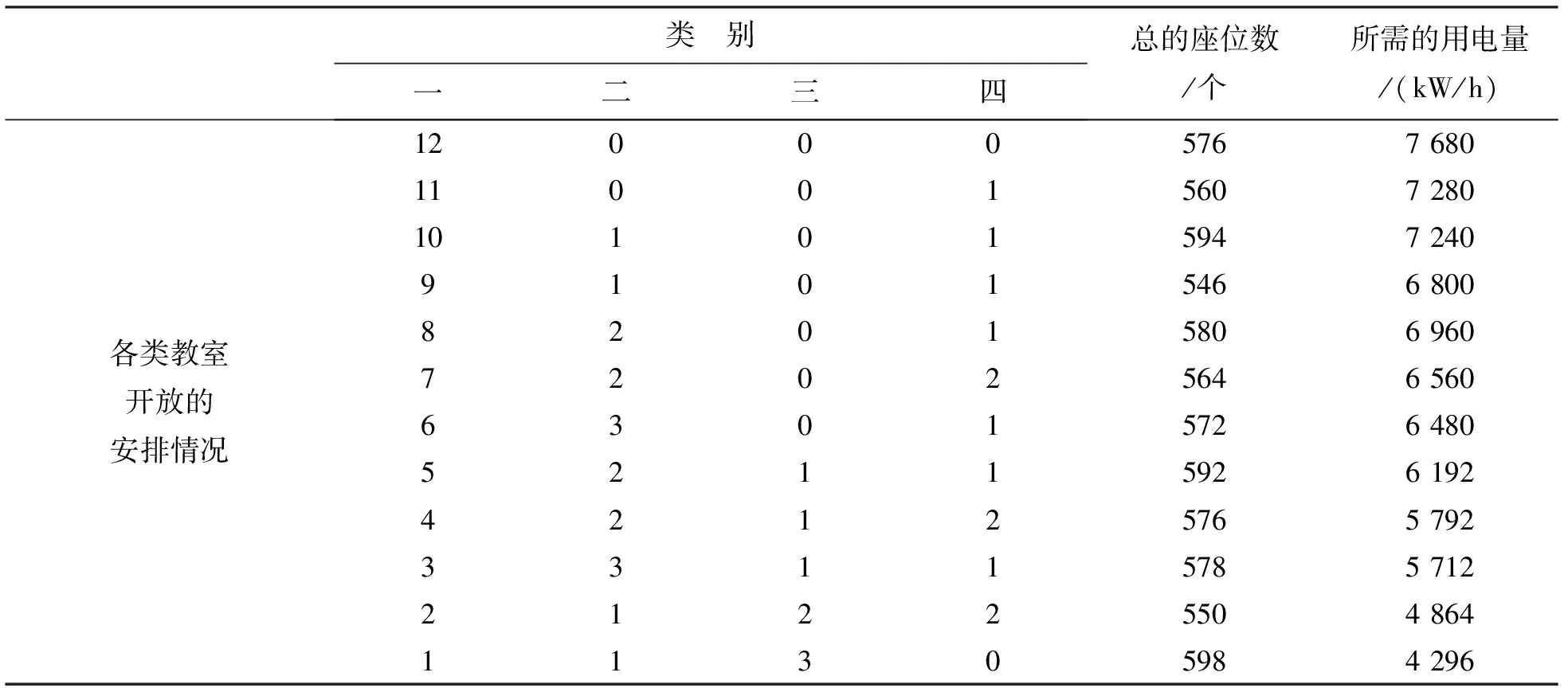
表2 调整后各类教室开放情况和用电量

这样在满足问题一中的约束条件，要使需要上自习的同学满足程度不低于90%，必须要安排的座位数满足同学们的需要，开放的满座率不低于4/5，同时尽量不超过90%，达到节约用电的目的。

综上所述，由表中数据分析可以，观察出怎样的开放教室可以是用电量最省，即第一类教室开放一个，第二类教室开放一个，第三类教室开放三个，第四类教室不开放，这样便得出所消耗用电量最小值为4 296 kw·h。

4.3 问题三的建立与求解

相对于问题一约束条件有所改变，上自习的人数增多，每个同学上自习的可能性增大为0.85，要求上自习的同学的满足程度不低于99%，开放的教室满座率不低于4/5，同时尽量不超过95%。

既要满足同学们的需要又要是用电量达到最省，可以参照问题一得求解模型对问题三进行求解；首先必须满足题中所给约束条件：即每个同学是否上自习是独立的，上自习的可能性是0.85，则可能上自习的人数：p=1 000×0.85=850。

要使需要上自习的同学满足程度不低于99%，必须要安排的座位数满足：

48x1+82x2+156x3+32x4≥850×99%

开放的满座率不低于4/5，同时尽量不超过95%，则要满足：

根据题中条件，来分析所需要的目标函数，既要使用电量达到最少，必须满足所给约束条件，再来建立线性规划的模型：

minZ=W1x1W2x2W3x3W4x4

运用LINGO进行编程求解得目标函数Z的最小值为3 692.4kW·h，相应的开放的教室数分别为：第一类教室开放9个；第二类教室开放2个；第三类教室开放2个；第四类教室开放1个。

综上所述，当教室开放个数按类别依次为9、2、2、1时，既满足了同学们的需要，又可以达到节省用电量的目的，即最省用电量为3 692.4kW·h。

当假设每个教室中每个灯管照亮座位的情况是一致的，开放的教室可以只打开部分灯管，要讨论在这种条件下各种情况的教室开放情况，为了达到更加节约用电的目的。可以做分析，即设各类教室开放分别为x1，x2，x3，x4，每个教室开关数分别为y1，y2，y3，y4，则开放教室的总座位数：

总的用电量：

Z=3×(40x1·4y1+50x2·4y2+48x3·6y3+60x4·2y4)

其约束条件：

在满足问题一的条件下，即S≥p×90%(p=1 000×0.6)

求解得：

根据上面的求解得模型的最优化方案：

(1) 各类教室开放情况。第一类教室不开放，第二类教室开放3间，第三类教室开放3间，第四类教室开放2间。(2) 各个教室灯管开关情况。第一类教室不开灯，第二类教室每间教室开8个灯管，第三类教室每间教室开24个灯管，第四类教室每间教室开4个灯管。

当满足假设条件三时，即

S≥p×99%(p=1 000×0.85)

根据模型用LINGO运行求解得：

根据上面的求解得模型的最优化方案为：

(1) 各类教室开放情况。第一类教室不开放，第二类教室开放3间，第三类教室开放3间，第四类教室开放2间。

(2) 各个教室灯管开关情况。第一类教室不开灯，第二类教室每间教室开16个灯管，第三类教室每间教室开24个灯管，第四类教室每间教室开4个灯管。

参考文献：

[1] 姜启源.数学模型(第3版)[M].北京：高等教育出版社，2003

[2] 胡富昌.线性规划[M].北京：中国人民大学出版社，1995

[3] 阳明盛，罗长童.最优化原理、方法及求解软件[M].北京：科学出版社，2006

[4] 罗国旺，郑航.基于FAHP和GRA的社会治安模糊综合评价模型研究[J].重庆工商大学学报：自然科学版，2013(8)：28-32

[5] 么慧慧，郑航，刘希梅.改进模糊评价法在企业经济效益中的应用[J].重庆工商大学学报：自然科学版，2013(5)：22-25