计算流体力学应用于子通道分析的初步方法研究

臧金光，闫 晓，黄善仿，曾小康，黄彦平

(1.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室，四川 成都 610041；

2.清华大学 工程物理系，北京 100084)

实际反应堆系统存在3种主要结构尺度：1) 系统分析尺度，着眼于整个反应堆系统的运行特性和响应特性；2) 子通道分析尺度，对反应堆堆芯采用准二维方法进行建模分析；3) 计算流体力学(CFD)尺度，针对系统中具有明显三维流场特征的区域进行计算分析。在开展反应堆系统分析时，为寻求精度与效率之间的平衡，同时兼顾不同尺度的物理现象，一个较为普遍的方法是采用多尺度耦合，针对不同尺度的结构选用相应尺度的分析程序。一些国家正在积极推进多物理、多尺度、多学科的数字化耦合平台研发，如美国的虚拟反应堆计划，欧盟的NURESIM耦合平台[1]等，还有一些研究者开发了一些具体的耦合程序，如CAST3M/ARCTURUS程序[2]，COBRA/CFX耦合程序[3]，RELAP5/CFD耦合程序[4]等。多物理、多尺度的耦合研究是当前研究的热点之一。

在开展热工水力多尺度分析时，人为地将各个尺度分解，针对不同尺度发展了各自的分析程序，然后再建立一耦合平台将分解后的程序重新组合在一起。实际上，各尺度的分析方法并不存在本质差别，它们均源于基本的流体力学控制方程，均基于相同或相近的本构关系式。例如，计算流体力学尺度的控制方程经过一定方法的统计平均和适当简化后可变成子通道控制方程和系统控制方程，因此，计算流体力学方法在理论上已具备求解子通道尺度和系统尺度的条件，从而为计算流体力学程序开展子通道尺度分析和系统尺度分析提供可能。

本工作即是基于计算流体力学方法开展子通道分析的一种尝试。本工作研究计算流体力学控制方程与子通道控制方程间的联系，然后通过一具体组件计算对本工作提出的子通道CFD方法进行比较和分析，为多尺度耦合分析提供一种新思路。

1 控制方程比较

计算流体力学方法所基于的控制方程是局部瞬时Navier-Stokes方程。局部瞬时Navier-Stokes方程是研究各尺度流体流动和传热的理论基础，子通道控制方程的理论形式是基于局部瞬时方程通过一定的数学变换和简化假设推导得到的[5-6]，借助的主要数学定理包括Leibnitz定理和Gauss定理。Leibnitz定理建立了空间积分与时间微分的交换关系，可将一体积分的时间变化率变换成一时间变化率的体积分与表面通量之和。Gauss定理揭示了高维积分与低维积分之间的关系，将散度的体积分转化成它的表面通量。推导子通道控制方程的重要假设是认为子通道的轴向流动起主要作用，子通道间的横向流动起次要作用，同时由于轴向尺度远大于横向尺度，一些量的轴向梯度可忽略。

进行积分平均不可避免地会带来信息缺失，引入信息缺失的因素包括：1) 基于类似边界层理论的假设，认为轴向尺度远大于横向尺度，一些物理量如黏性应力、雷诺应力等的轴向梯度项可忽略；2) 忽略了各物理场的细致截面分布，认为积分运算与其他代数运算具有普遍的可交换性，如认为〈ρv〉=C1〈ρ〉〈v〉，〈v2〉=C2〈v〉2，其中，ρ为密度，v为速度，分布系数C1和C2一般假设为1；3) 由于认为横向动量方程在子通道控制方程中不起重要作用，因此在处理横向动量方程时作了很多简化，子通道交界面处的湍流交混通过简单的交混因子进行封闭。大部分情况下，这些假设均是合理的。

将CFD工具运用于子通道分析的前提是二者的控制方程具有统一性，为说明这一问题，以连续性方程为例来介绍二者之间的联系[5-6]。

CFD方法的连续性方程的形式为：

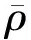
对上式进行体积平均，认为控制体固定，且积分与微分之间可交换：

其中：〈〈〈 〉〉〉为体积平均算符；t为时间坐标；x、y、z为空间坐标。

再应用Gauss定理，转化成子通道的控制方程形式为：

即经过积分后的子通道质量守恒方程本质上相当于以子通道平均量为变量的局部微分方程。对于动量守恒方程和能量守恒方程，可采用类似的方法分析。另外基于CFD工具的子通道分析方法也可考虑子通道间的横向流动，这种横向流动主要依靠横向的压力梯度驱动。CFD控制方程与子通道控制方程间的联系为将CFD方法应用于子通道分析打下了基础。

2 方法验证及结果分析

为进一步验证将CFD方法应用于子通道分析的可行性，选取了中国核动力研究设计院提出的超临界水冷堆概念设计方案中的CSR1000组件作为分析对象，分别用基于CFX软件的精细CFD方法(CFX-CFD)、基于CFX软件的子通道方法(CFX-SUB)及基于子通道程序ATHAS的子通道分析方法开展了计算分析，并比较了三者计算结果的差异。

CSR1000组件采用小组件的设计方案[7]，1个大组件含有4个小组件，每个小组件由φ9.5 mm燃料元件呈9×9方形布置，中间水棒占有5×5栅元位置，燃料元件分别位于周围两排，具体几何参数及计算工况列于表1。CSR1000原型组件采用绕肋进行自定位，这里先对光滑组件进行分析，为绕肋的性能评价提供参考。由于组件在几何上具有1/8对称性，为节省计算资源，选取1/8结构进行分析，组件形状及各子通道编号示于图1。

表1 几何参数及计算工况

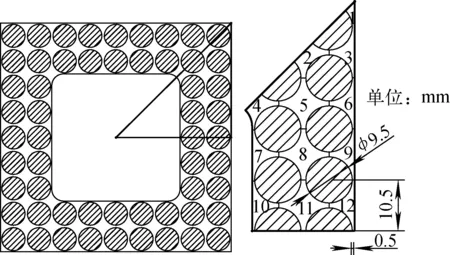
图1 CSR1000组件及子通道编号

CFX-CFD方法即为常规的CFD方法，对组件通道划分精细网格，然后开展CFD计算。本次计算选用SST湍流模型。为保证计算结果的有效性，开展了网格的无关性分析。图2示出不同网格参数下通道摩擦系数与中心通道平均换热系数的对比。由图2可见，当网格数为230万时，就已满足了网格无关性要求。

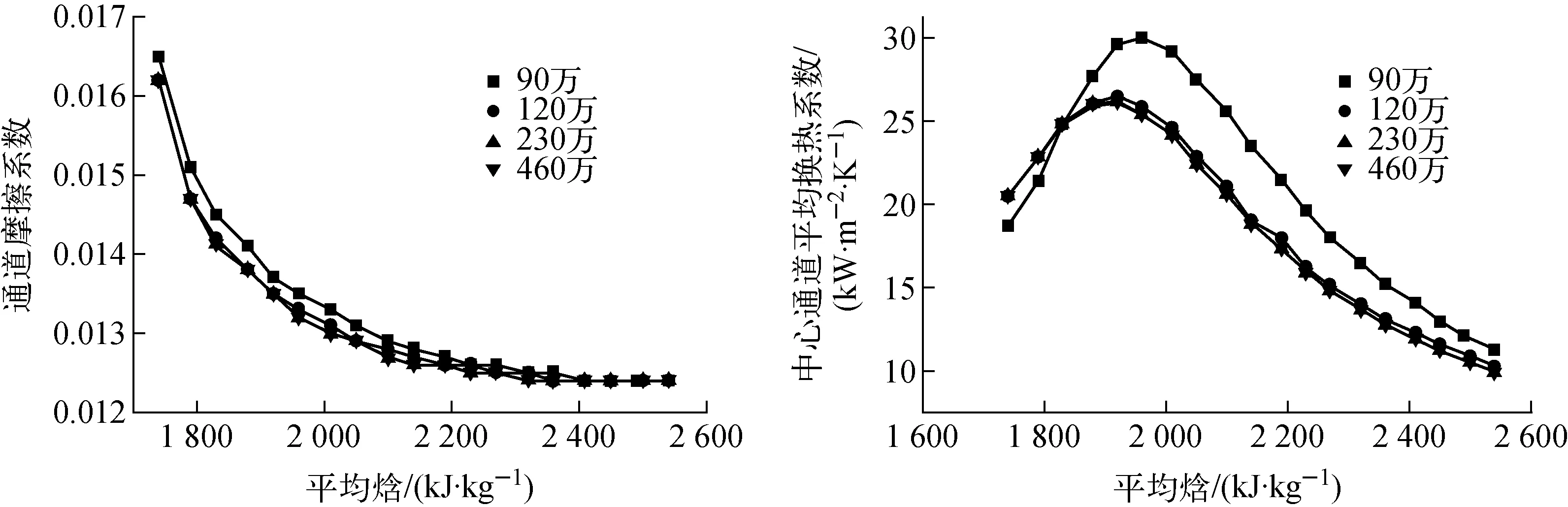
图2 网格无关性分析结果

CFX-SUB方法是利用CFX工具完成子通道分析的功能，以每个冷却剂通道作为网格的划分尺度，每个子通道截面只划分1个网格。这样进行网格划分的结果是CFX软件无法计算壁面的剪切应力分布，需通过附加体积力的方式把摩擦力加入到轴向动量方程中。选用Blausius公式计算摩擦系数。燃料元件表面的热流密度也需采用转化成体积热源的方式添加到轴向能量方程中，记表面热流密度为qs，子通道流通面积为A，热周为Pt，热力直径为Dt，转化后的等效体积热流密度qv的表达式为：

在CFX软件中，将每个子通道作为一流体计算域，子通道与子通道之间通过交界面连接，在每个计算域中设置对应的体积热源和阻力源。由于只有1层网格，CFX软件无法识别壁面，也无法对壁面进行求解，因此每个计算域除入口、出口、交界面等边界条件外，其他边界均设置成对称边界条件。当子通道数目较多时，手动为每个子通道设置条件会很繁琐，CFX软件支持CCL命令语言和Perl脚本语言，用于对边界条件进行批量设置，可有效简化设置的工作量。

由于CFX-SUB方法只能得到子通道的平均质量流速和平均温度，因此首先借助CFX-CFD方法初步分析组件内的流场分布特征。图3示出基于CFX-CFD方法得到的出口质量流速和温度的分布。CFX-CFD方法可得到通道截面各位置的流场信息，截面质量流速与温度的分布在子通道中心与最窄间隙处存在明显的分布不均。由于子通道中心的流通截面较大，流动阻力较小，流体在各子通道进行流量分配时更倾向于流向宽通道处，而窄通道的质量流速相对较低，局部位置的最大质量流速和最小质量流速相差接近两倍。这种不均衡的质量流量分配进一步造成同一截面上的温度分布存在明显差异。由于超临界水在拟临界点前后物性变化较大，窄间隙内的流体会提前跨过拟临界点，导致密度迅速下降，这又反过来继续增加了流动阻力，迫使流体继续向宽通道处流动。这样，在元件与元件之间以及元件与组件盒之间的狭窄间隙内，很容易出现局部的过热流体。这说明稠密布置的燃料组件中需要考虑采用一些附加设计(如绕丝等)以避免局部高温流体的出现。

子通道分析程序ATHAS[5]可用来开展超临界条件下的子通道分析。图4比较了CFX-CFD、CFX-SUB、ATHAS 3种方法计算的出口焓与质量流速G的分布。由图4可见，各子通道中，3种方法预测的出口焓与质量流速分布趋势整体相同。相同类型子通道的出口焓和质量流速相差较小，如中心通道(编号为2，5，8，11)的质量流速稳定在1 000 kg/(m2·s)左右，边通道(编号为3，6，7，9，10，12)的质量流速在700 kg/(m2·s)左右。尽管相同类型子通道由于与相邻通道交混性能的不同而有所差异，但整体上保持了相似的热工水力特性。另外，不同类型子通道由于在几何结构方面的显著差异，在吸热量和质量流速方面有明显不同。CFX-SUB方法预测的各子通道平均值的整体趋势与CFX-CFD方法的较为接近。以CFX-CFD方法计算的结果作为参考，CFX-SUB计算的平均焓的最大相对误差出现在1号子通道，平均质量流速的最大相对误差出现在8号子通道，二者的最大相对误差均不超过20%。CFX-SUB方法可反映出角通道过热、中心通道较为均匀的变化趋势，可见CFX-SUB方法的预测结果是合理的。另一方面，CFX-SUB方法预测的各子通道之间的差别比CFX-CFD方法和ATHAS程序的计算结果要大些，CFX-SUB方法预测的1号子通道的流体温度过高与其预测的质量流速较低相对应。

图3 CFX-CFD方法的计算结果

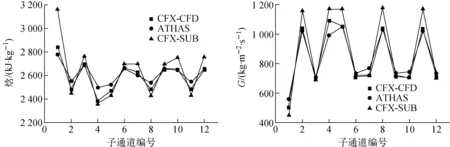
图4 3种方法计算结果对比

为进一步分析CFX-SUB与CFX-CFD方法计算结果的异同，图5进一步比较了二者在角通道(编号为1)、中心通道(编号为2)和边通道(编号为3)3种典型子通道的沿程温度T和质量流速的变化。由图5可见：CFX-SUB方法预测的整体趋势与CFX-CFD方法的一致，中心通道沿程质量流速上升，边通道和角通道沿程质量流速下降；角通道的温度分布上升较快，其次是边通道，中心通道的温度上升最为平缓。尽管如此，CFX-SUB方法预测的角通道的流体温度明显高于CFX-CFD方法，而预测的角通道的质量流速的差别却没有这么大。

CFX-SUB方法未正确考虑子通道交界面上的湍流交混，导致子通道间流体热交换能力减弱。子通道交界上的湍流交混是子通道间能量交换的重要方式，由于交界面上的涡团脉动，使得两个子通道内的流体微团产生净能量交换。在推导子通道控制方程中，引入了湍流热通量的二阶相关统计项，使得方程组不封闭。为解决这种不封闭问题，子通道程序中通常定义湍流交混系数——无量纲数β来表征相邻子通道之间的能量交换量。

图5 CFX-CFD与CFX-SUB方法计算结果的比较

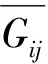
为了分析湍流交混系数对子通道分析计算结果的影响，使用ATHAS程序计算了不同湍流交混系数下各子通道的温度t的分布(图6)。随着湍流交混系数的降低，角通道的流体出口温度逐步上升，当湍流交混系数降至0.001时，ATHAS计算的角通道流体出口温度与CFX-SUB方法计算的结果相近。可见，CFX-SUB方法计算结果偏高的原因很有可能是未考虑子通道间的湍流交混，需要在后续的工作中改进。

图6 湍流交混因子影响分析

3 结论

多尺度热工水力耦合是目前开展反应堆安全分析的一种发展趋势，普通的做法是通过建立不同程序的数据交换平台来实现。本工作提出另外一种开展多尺度耦合的思路，以计算流体力学方法为手段，开展宏观的多尺度分析，并以子通道分析为例验证这种方法，得到的主要结论如下。

1) 计算流体力学方法既可用于满足连续介质假设的流体微团分析，又可用于子通道尺度或更大尺度的流体问题分析，区别不同尺度的模拟在于网格尺度的大小及对于几何结构的描述能力。通过对子通道控制方程和局部瞬时控制方程的对比，认为子通道守恒方程本质上相当于以子通道平均量为变量的局部微分方程，从理论上说明了计算流体力学应用于子通道分析的可能性。

2) 以一典型组件为例，分别采用计算流体力学方法、子通道方法及计算流体力学应用于子通道这3种方法进行计算，并对计算结果进行比较分析，说明了计算流体力学应用于子通道方法的合理性以及具体操作的可实现性。另外，由于新方法中尚未考虑子通道间的湍流交混，使得这种方法仍存在进一步的改进空间。

参考文献：

[1] CHAULIAC C, ARAGONÉS J M, BESTION D, et al. NURESIM: A European simulation platform for nuclear reactor safety: Multi-scale and multi-physics calculations, sensitivity and uncertainty analysis[J]. Nuclear Engineering and Design, 2011, 241(9): 3 416-3 426.

[2] STUDER E, BECCANTINI A, GOUNANDA S, et al. CAST3M/ARCTURUS: A coupled heat transfer CFD code for thermal-hydraulic analyzes of gas cooled reactors[J]. Nuclear Engineering and Design, 2007, 237(15): 1 814-1 828.

[3] 刘余，张虹，贾宝山. COBRA-Ⅳ与CFX程序耦合研究[J]. 核动力工程，2010，31(2)：43-46.

LIU Yu, ZHANG Hong, JIA Baoshan. Research on coupling of COBRA-Ⅳ and CFX[J]. Nuclear Power Engineering, 2010, 31(2): 43-46(in Chinese).

[4] ANDERSON N, HASSAN Y, SCHULTZ R. Analysis of the hot gas flow in the outlet plenum of the very high temperature reactor using coupled RELAP5-3D system code and a CFD code[J]. Nuclear Engineering and Design, 2008, 238(1): 274-279.

[5] 单建强，李昌莹，陈伟. 子通道分析程序ATHAS理论说明书[R]. 西安：西安交通大学，2008.

[6] 郝老迷. 沸腾传热与气(汽)液两相流动[M]. 北京：核工业研究生部，2007.

[7] 夏榜样，杨平，王连杰，等. 超临界水冷堆CSR1000初步概念设计[J]. 核动力工程，2013，34(1)：9-14.

XIA Bangyang, YANG Ping, WANG Lianjie, et al. Core preliminary conceptual design of supercritical water-cooled CSR1000[J]. Nuclear Power Engineering, 2013, 34(1): 9-14(in Chinese).