超轻多孔类蜂窝夹心结构创新构型及其力学性能
李响,周幼辉,童冠,喻里程,李阳,张洵
(1.三峡大学水电机械设备设计与维护湖北省重点实验室, 443002, 湖北宜昌; 2.三峡大学机械与动力学院, 443002, 湖北宜昌; 3.新能源微电网湖北省协同创新中心(三峡大学), 443002, 湖北宜昌)
超轻多孔类蜂窝夹心结构创新构型及其力学性能
李响1,2,3,周幼辉2,童冠2,喻里程2,李阳2,张洵2
(1.三峡大学水电机械设备设计与维护湖北省重点实验室, 443002, 湖北宜昌; 2.三峡大学机械与动力学院, 443002, 湖北宜昌; 3.新能源微电网湖北省协同创新中心(三峡大学), 443002, 湖北宜昌)
通过优化排列六边形和四边形夹心胞元,以六边形和四边形的组合设计胞元结构,提出了类蜂窝夹层结构的概念并对其进行了创新构型;基于Gibson提出的胞元理论,建立了类蜂窝夹心结构力学等效模型,并推导出了等效模型的等效弹性常数公式。以卫星结构的蜂窝夹层板作为应用实例,对类蜂窝和正六边形蜂窝夹心结构的等效力学常数进行了计算对比,结果表明:两者的等效弹性模量近似相等,然而类蜂窝夹心结构的等效剪切模量却有较大提高,同时等效密度更小,可有效减小结构的质量。对卫星结构类蜂窝夹心结构进行了数值模拟研究,验证了类蜂窝夹心结构力学等效模型的正确性。
夹层结构;类蜂窝;等效弹性常数;力学性能
作为高效率、能源节约型复合材料及其结构的典型代表,夹层结构材料具有重量轻、比强度和比刚度高、稳定性好等众多优点,它将面板的高强度和高模量与夹心的低密度和高刚度有机结合起来,在航空航天、汽车、船舶、机械、建筑等领域中有着极其重要的应用价值。
随着夹层结构材料在工程领域中的不断推广应用,对夹层结构材料的比强度、比刚度、稳定性、抗疲劳、耐热性、结构尺寸等性能指标提出了更高的要求,包括蜂窝夹层结构在内的传统夹层结构材料已逐渐不能满足工程设计要求,迫切需要开发新型的夹层结构材料。目前出现的包括Kagome、X-core等夹层结构在内的多种新型夹层结构[1],引起了国内外许多研究者的兴趣并进行了深入研究。然而,这些新型夹层结构由于其夹心层结构较为复杂,导致了加工困难,并且依赖于新型高精度制造工艺的开发,制造成本偏高,使得这些新型夹层结构不能在工程中得到推广应用。目前,蜂窝夹层结构[2]是设计理论和制造工艺技术最为成熟和应用最广的夹层结构类型之一,主要以六边形蜂窝夹心结构(如图1a所示)为主,也包括四边形、三角形等规则蜂窝夹心结构,已广泛应用于航天飞机、船舶、汽车等运载工具,并逐步被运用到大型平板类零部件的轻量化设计中,具有广阔的市场前景。同时,针对蜂窝夹层结构的结构优化设计、力学性能、加工工艺、强度和刚度特性等方面的研究依然在不断深化、创新。基于上述背景,针对目前成熟的蜂窝夹层结构进行改进设计或创新构型,将具有重要的创新意义和工程应用价值。
1 类蜂窝夹心结构创新构型
夹心是夹层结构的重要组成部分,合理的夹心结构可以大大减轻夹层结构的重量。随着新型制造工艺的快速发展,根据不同的应用目的和工程需求,夹心被设计成多种结构形式,主要包括蜂窝夹心、泡沫夹心、桁架夹心等。作者基于前期的研究基础[3-7],从仿生学和创新构型的角度出发,提出了“类蜂窝”夹层结构的概念,即拟通过优化排列六边形和四边形夹心胞元,设计合适的六边形和四边形组合胞元结构,构造新型类蜂窝夹层结构,如图1b、1c所示。为了更好地揭示该类蜂窝夹层结构的特点,本文将针对其力学性能进行详细的分析。

(a)六边形蜂窝夹心结构

(b)类蜂窝夹心结构
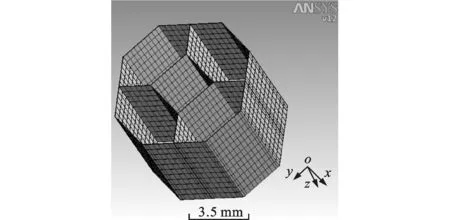
(c)类蜂窝夹心胞元
2 类蜂窝夹心结构力学性能分析
夹心结构包括微观结构和宏观结构。为了更好地对夹心层的微观和宏观结构的力学性能进行研究,有必要建立一个等效模型,以便能从总体上同时反映夹心结构的微观性能和宏观性能。为此,本文引入夹心结构力学等效模型的概念。
定义:基于夹心层的微观结构和整个夹心层宏观结构的力学性能,建立一个均质的正交异型层,与原有夹心结构具有等同的力学性能,称之为夹心结构力学等效模型。夹心结构力学等效模型的等效过程如图2所示。
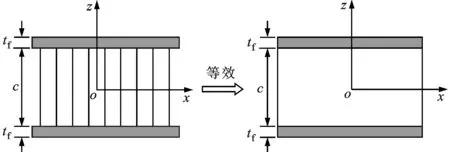
(a)夹心结构 (b)力学等效模型
目前,针对夹心结构力学等效模型的研究工作主要集中在蜂窝夹心结构。以Gibson为代表的国内外学者围绕蜂窝夹心结构的力学性能做了一定的工作,建立了多种夹心结构分析模型。使用这些模型的前提是要先确定夹心结构力学等效模型的弹性常数,因此Gibson提出了经典的胞元理论[8]。目前,有关蜂窝夹心结构的等效弹性常数的研究工作绝大部分是在胞元理论的基础上展开的[9-11]。本文在已有研究的基础上,运用传统的材料力学理论知识,对类蜂窝夹心结构的力学等效模型进行分析和求解。
将类蜂窝夹心层中最基本的六边形和四边形组合单元定义为胞元。类蜂窝夹心结构是周期性排列的胞元阵列,每个胞元由4个规则六边形通过胶黏剂黏结而成,中间围成正方形。胞元的结构和几何尺寸如图3所示,几何参数包括:六边形短边长度l(mm),正方形边长h(mm),胞元厚度t(mm),六边形短边与水平方向的夹角θ(°)。

(a)胞元结构
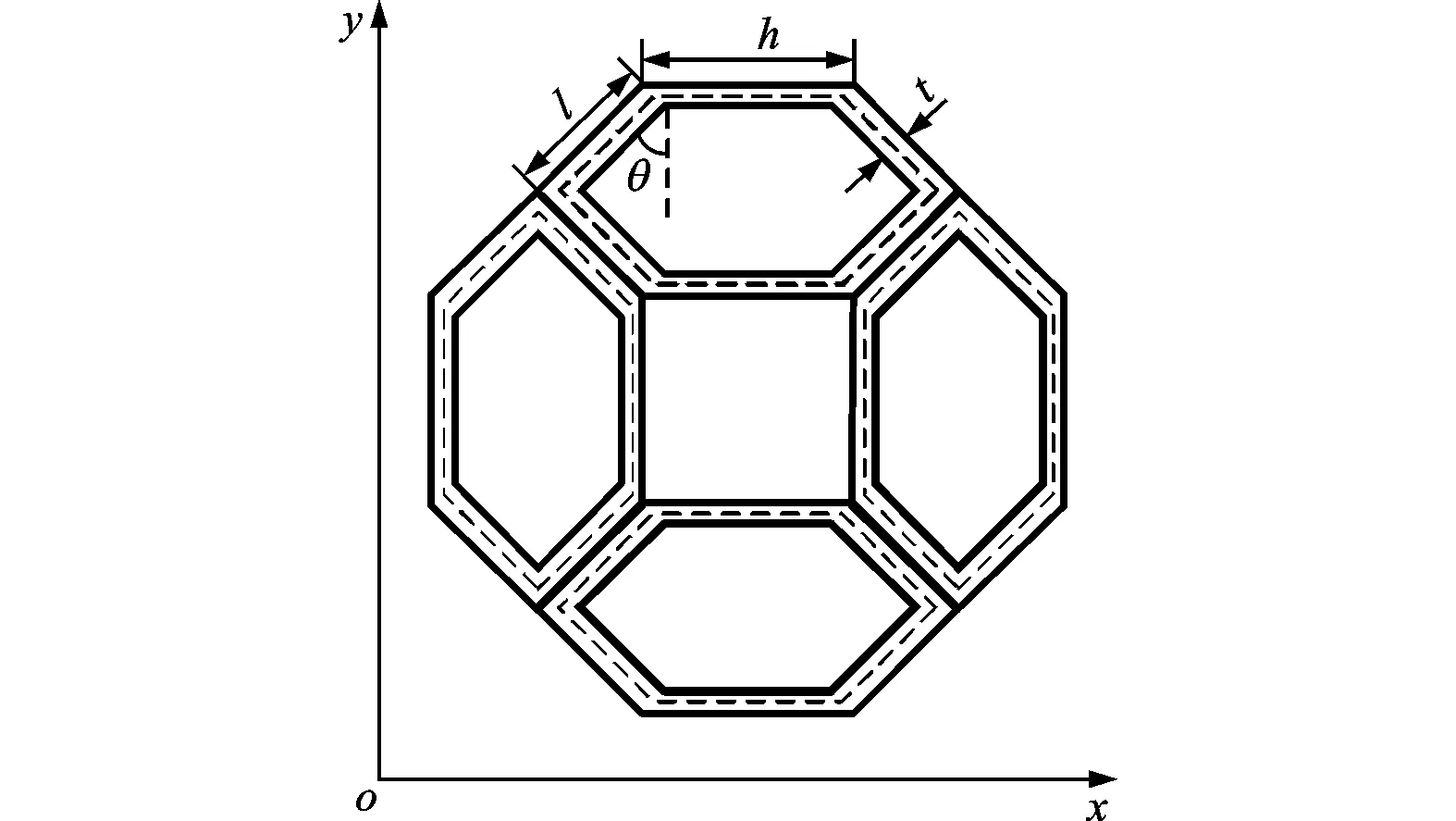
(b)几何尺寸
为了对类蜂窝夹心结构的等效力学性能进行分析,在充分考虑胞元壁板的伸缩变形的前提下,可建立如图4所示的胞元简化模型。
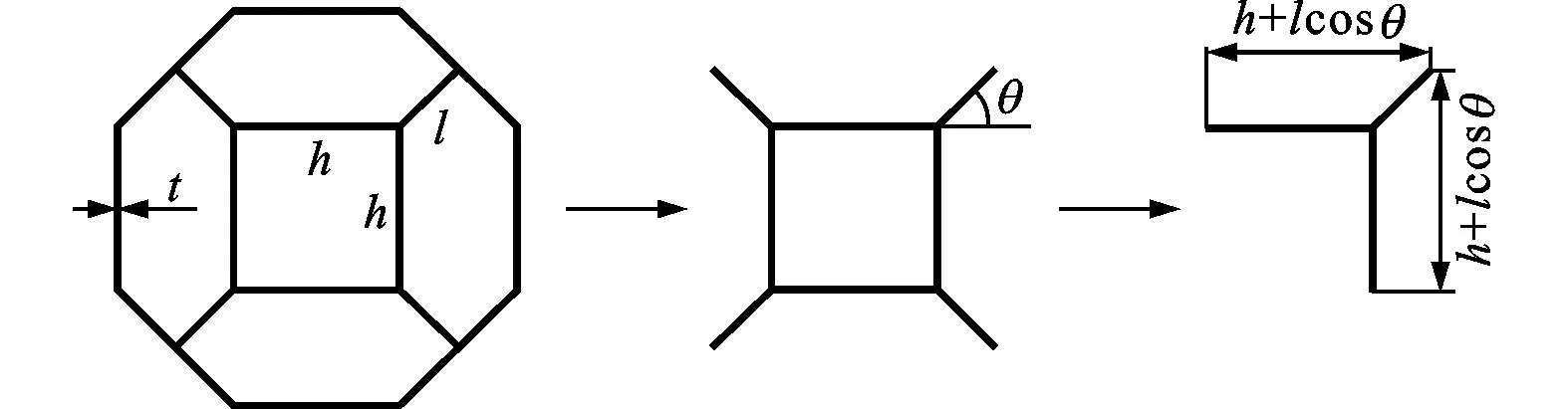
图4 胞元的简化模型
运用力的平衡原理、材料力学中的梁弯曲理论和质量守恒定律等相关知识,对类蜂窝夹心层的等效力学性能参数进行求解,如图5所示。
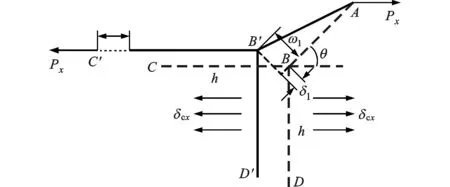
(a)x方向的单向拉伸
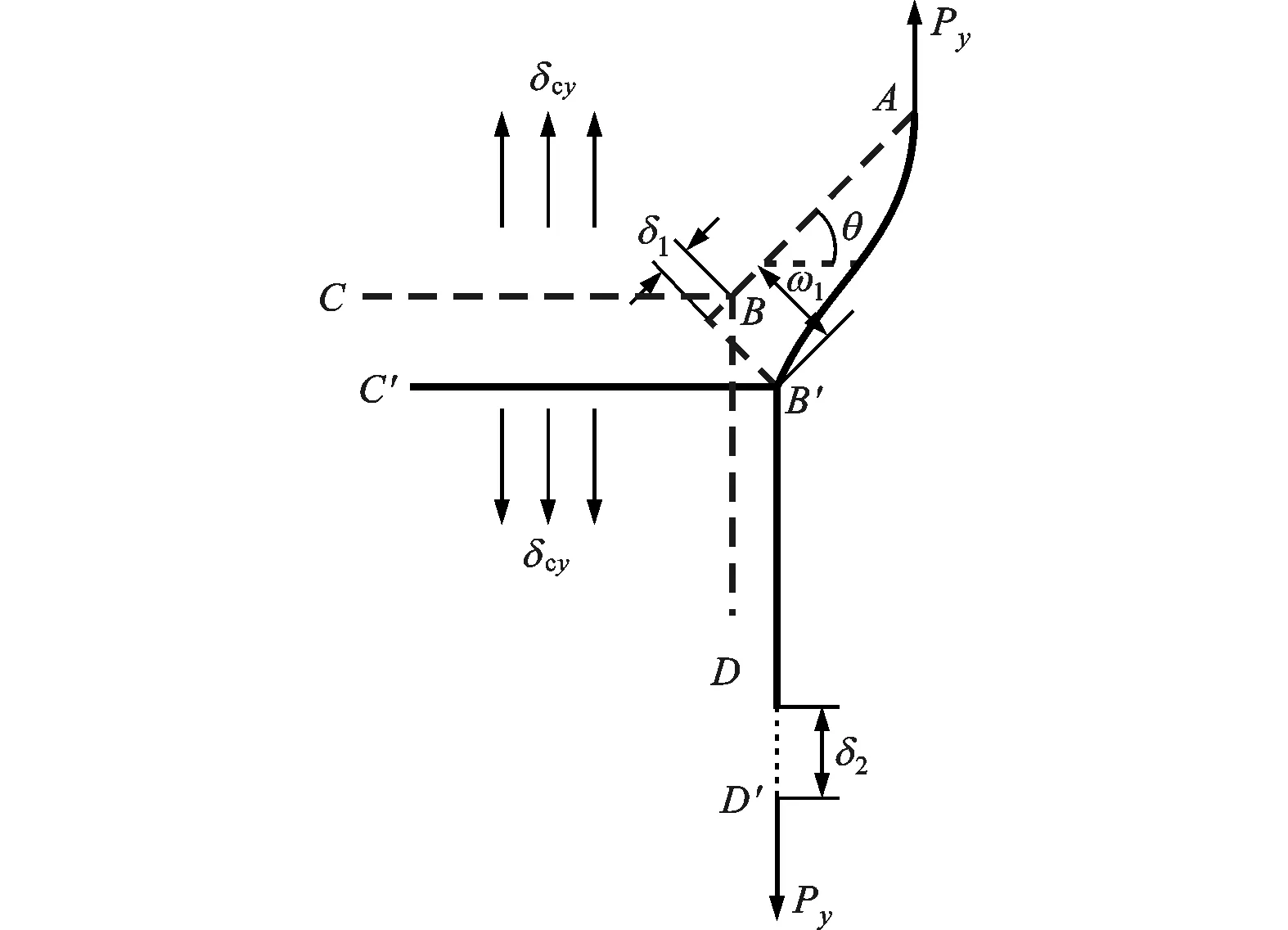
(b)y方向的单向拉伸
2.1 夹心在x方向的等效弹性常数推导
如图5a所示,根据力的平衡条件得
∑MA=0
(1)
-M-M+Pxsinθ=0
(2)
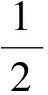
(3)
Px=δcxAx=δcx(h+lsinθ)b
(4)

(5)
式中:M为夹心胞元节点的弯矩,N·m;Px为夹心胞元节点所受的外力,N;Ax为夹心胞元x方向的受力截面积,m2;δcx为胞元在x方向的应变;b为夹心胞元壁板的高度,m。
根据材料力学中的梁弯曲理论,可知壁板AB的挠度
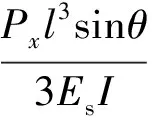
(6)
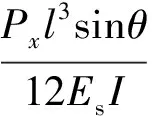
(7)
式中:Es为夹心材料的弹性模量;I=bt3/12为惯性矩。将I代入式(7)中可得
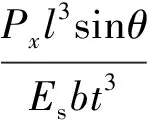
(8)
根据虎克定律,在外力Px的作用下胞元壁板AB和BC的拉伸量分别为
(9)
(10)
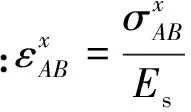
由虎克定律可得在x方向上的等效应变

(11)
将式(8)~式(10)代入式(11),可得
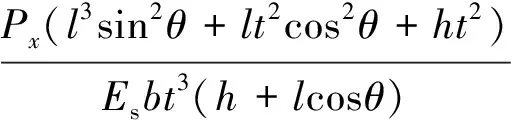
(12)
同理,可以得到在y方向上的等效应变


(13)
根据泊松比的定义,可知类蜂窝夹心在x方向上的等效泊松比
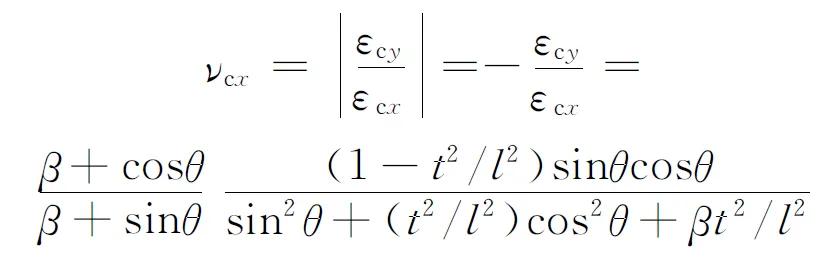
(14)
式中:β=h/l。根据弹性模量的定义,可知类蜂窝夹心在x方向的等效弹性模量
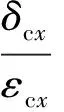
(15)
2.2 夹心在y方向的等效弹性常数的推导
与上节同理,根据图5b可求得类蜂窝夹心在y方向上的等效弹性常数Ecy和νcy的表达式
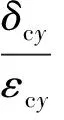
(16)

(17)
2.3 夹心的等效密度计算
根据图3和图4,胞元体积
V1=4bt(h+l)
(18)
胞元质量
m1=ρsV1=4bt(h+l)ρs
(19)
式中:ρs为夹心材料的密度,kg/m3。
胞元的等效实体模型的等效体积
Vce=b(h+2lsinθ)(h+2lcosθ)
(20)
等效实体模型的质量
mce=ρcVce=ρcb(h+2lsinθ)(h+2lcosθ)
(21)
式中:ρc为夹心的等效密度,kg/m3。
根据等效前、后的质量守恒原理,mce=m1,因此可得
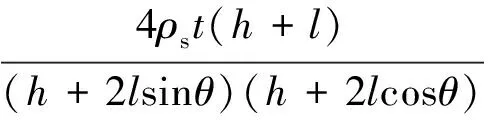
(22)
由于夹心壁板的伸缩变形主要是纵向变形,对蜂窝夹心在xy平面上的等效横向剪切模量Gcxy影响不大,因此可以采用Gibson公式中的Gcxy表达式。
经过推导,可得类蜂窝夹心层的等效力学性能参数表达式如下

(23a)

(23b)

(23c)
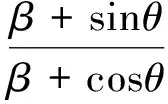
(23d)

(23e)
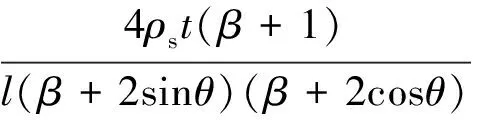
(23f)
3 实例分析与对比
取θ=45°,h=l,β=1,式(23)可简化为

(24a)

(24b)

(24c)

(24d)

(24e)

(24f)
对于具有相同胞元厚度t的六边形蜂窝夹心层,当取θ=30°、l=h、β=1时,根据其等效力学性能参数公式[4,8],相应的公式可简化为
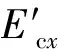
(25a)

(25b)
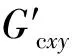
(25c)
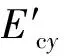
(25d)
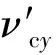
(25e)
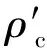
(25f)
为了便于直观地进行比较,令n为类蜂窝结构和正六边形蜂窝结构对应的等效力学性能参数之比,t2/l2≈0,可得如下结果
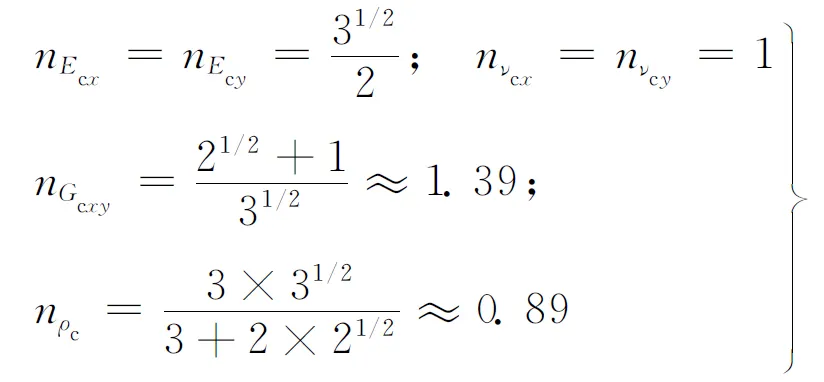
(26)
式(26)成立的前提条件是胞元厚度t相等。为了更直观地反映类蜂窝夹心结构等效弹性参数的提高,不妨设类蜂窝夹心胞元和正六边形蜂窝夹心胞元的等效密度相等,此时式(26)可演变为
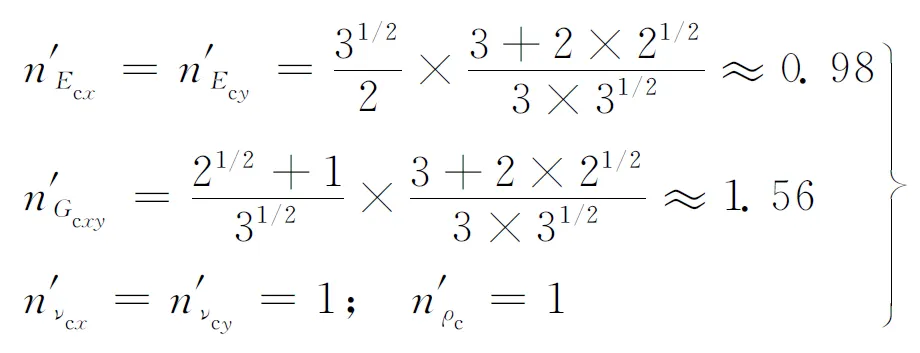
(27)
从式(27)可以看出,在类蜂窝夹心胞元和正六边形蜂窝夹心胞元质量相等的情况下,类蜂窝夹心结构和正六边形蜂窝夹心结构的等效弹性模量近似相同,但是等效剪切模量却有较大幅度的提高。
选取某卫星结构上采用的蜂窝夹层板[12]作为实例。该蜂窝夹层板的夹心为正六边形蜂窝,采用2024铝合金,材料的屈服强度为758 MPa,密度ρs=2780kg/m3,其他数据见表1。

表1 某卫星结构铝合金蜂窝夹层板的结构参数
根据式(25)和式(26)可以分别求得类蜂窝夹心结构和正六边形蜂窝夹心结构的等效弹性常数,结果见表2。

表2 类蜂窝夹心结构和正六边形蜂窝夹心结构等效模型的力学性能参数
由式(26)和表2的结果可以看出,在胞元厚度相等的情况下,类蜂窝夹心层与正六边形蜂窝夹心层相比,其等效弹性模量虽有所减小,但是其等效剪切模量却有较大提高,同时等效密度更小,有效地减小了结构的重量,具有更加优越的性能。
4 数值模拟
为了验证式(25)的正确性,利用ANSYS Workbench软件对卫星结构的类蜂窝夹层板结构进行数值模拟分析,建立的有限元模型如图6所示。

图6 类蜂窝夹心胞元有限元模型
取长×宽×高为0.1 m×0.1 m×0.0244m的类蜂窝夹心结构,对其分别施加x、y和z方向的应力(σcx,0,0)T、(0,σcy,0)T和(0,0,τcxy)T进行有限元模拟,结果如图7~图9所示。
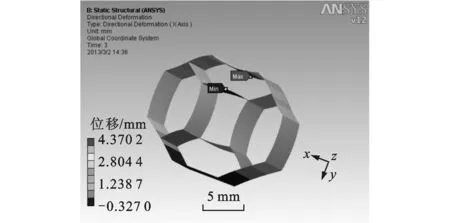
(a)x方向位移云图
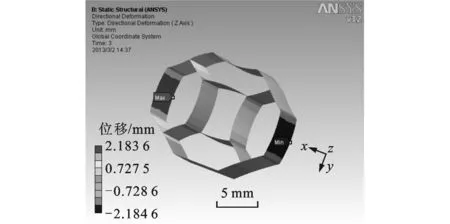
(b)y方向位移云图

(a)x方向位移云图
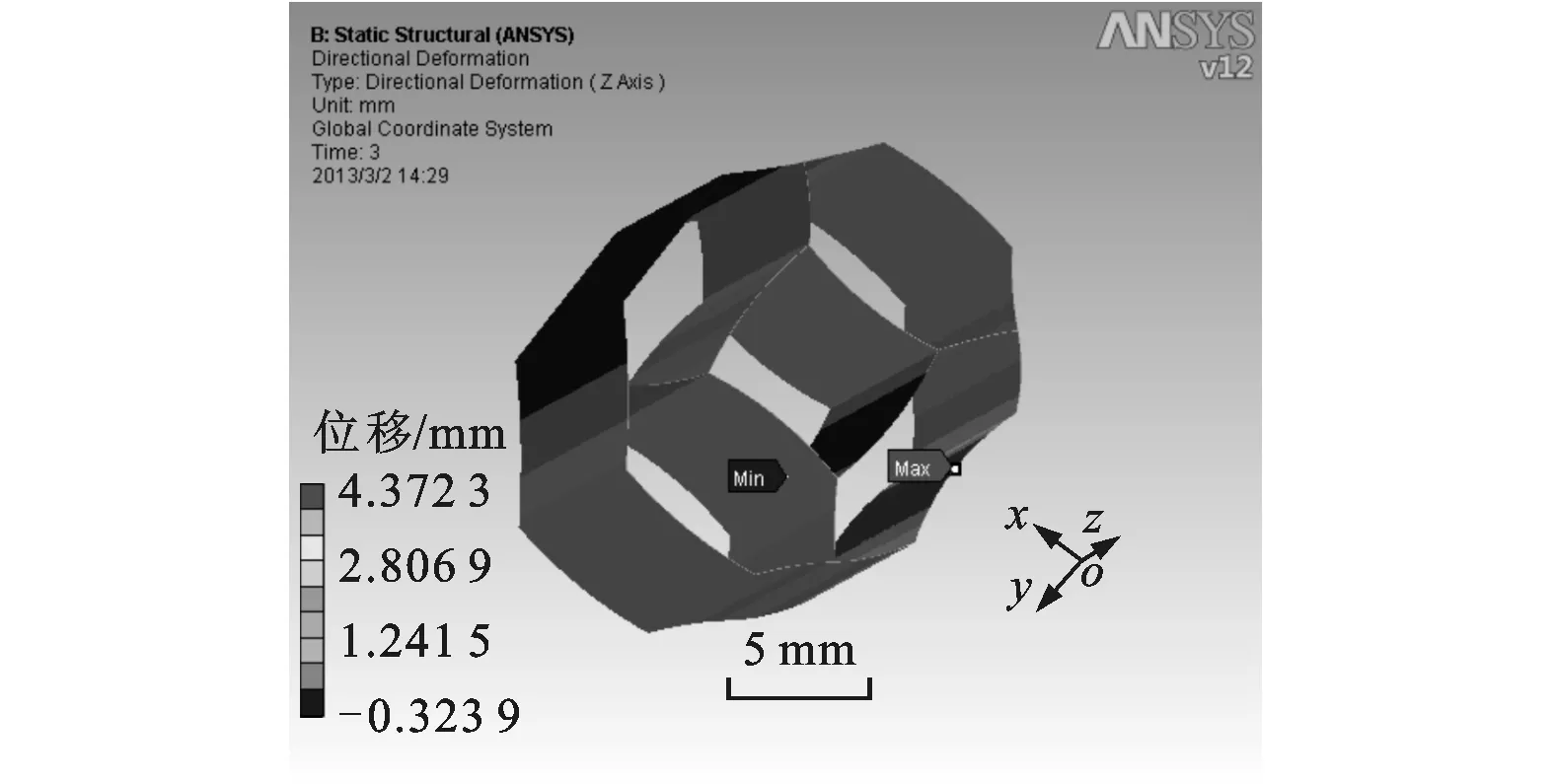
(b)y方向位移云图

(a)y方向位移云图

(b)等效应力云图
根据理论计算和模拟分析,分别得到类蜂窝夹心等效模型的弹性常数,见表3。从表3可以看出,理论计算和模拟分析结果基本吻合,由此验证了类蜂窝夹心结构力学等效模型的正确性。
表3 类蜂窝夹心结构等效模型弹性常数的理论计算值和模拟值

结果Ecx/MPaEcy/MPaνcx理论值0.14000.14000.9996模拟值0.13300.13280.9654结果νcyGcxy/MPa理论值0 99960 0562模拟值0 96150 0584
5 结 语
本文基于前期有关蜂窝夹心结构的研究成果,提出了类蜂窝夹层结构的概念,并对其夹心结构进行了创新构型。在此基础上,运用Gibson经典胞元理论和材料力学的相关理论,对类蜂窝夹心结构的等效力学性能进行了详细分析与推导,将类蜂窝夹心结构等效力学性能参数推导公式与正六边形蜂窝夹心结构的理论推导公式进行了对比分析,并结合具体实例进行了计算和模拟验证。研究结果表明,本文提出的新型类蜂窝夹心结构的力学性能优于常规蜂窝夹心结构的力学性能。
[1] PARK J, JOO J, LEE B, et al. Mechanical behaviour of tube-woven Kagome truss cores under compression [J]. International Journal of Material Sciences, 2011, 53(1): 65-73.
[2] VINSON J R. The behaviour of sandwich structures of isotropic and composite materials [M]. Lancaster, PA, USA: Technomic Publishing Co. Inc., 1999: 1-3.
[3] 李响. 承载夹层复合材料的轻量化设计方法及其应用研究 [D]. 武汉: 武汉理工大学, 2011.
[4] LI Xiang, LI Gangyan, WANG Chun H, et al. Minimum-weight sandwich structure optimum design subjected to torsional loading [J]. Applied Composite Materials, 2012, 19(2): 117-126.
[5] LI Xiang, LI Gangyan, WANG Chun H. Optimum design of composite sandwich structures subjected to combined torsion and bending loads [J]. Applied Composite Materials, 2012, 19(3/4): 315-331.
[6] 李响, 李刚炎, 游敏, 等. 多载荷约束夹层结构轻量化设计及应用 [J]. 武汉理工大学学报, 2011, 33(8): 138-141.
LI Xiang, LI Gangyan, YOU Min, et al. Sandwich structure lightweight design subjected to multiple loading constraints and its application [J]. Journal of Wuhan University of Technology, 2011, 33(8): 138-141.
[7] LI Xiang, YOU Min. Mechanical property analysis and numerical simulation of honeycomb sandwich structure’s core [J]. Advanced Materials Research, 2013, 631/632: 518-523.
[8] GIBSON L J. Modelling the mechanical behavior of cellular material [J]. Master Science and Engineering, 1989, A110: 1-36.
[9] ALLEN H G. Analysis and design of structural panels [M]. Oxford, UK: Pergamon Press, 1969.
[10]富明慧, 尹久仁. 蜂窝芯层的等效弹性参数 [J]. 力学学报, 1999, 31(1): 113-118.
FU Minghui, YIN Jiuren. Equivalent elastic parameters of the honeycomb core [J]. Acta Mechanica Sinica, 1999, 31(1): 113-118.
[11]梁森, 陈花玲, 陈天宁, 等. 蜂窝夹芯结构面内等效弹性参数的分析研究 [J]. 航空材料学报, 2004, 24(3): 26-31.
LIANG Sen, CHEN Hua-ling, CHEN Tian-ning, et al. Analytical study of the equivalent elastic parameters for a honeycomb core [J]. Journal of Aeronautical Materials, 2004, 24(3): 26-31
[12]李响, 游敏. 卫星夹层结构夹芯层力学性能分析与数值模拟 [J]. 三峡大学学报: 自然科学版, 2012, 34(4): 77-80.
LI Xiang, YOU Min. Mechanics performance analysis and numerical simulation of sandwich structure’s core for satellite [J]. Journal of China Three Gorges University: Nature Sciences, 2012, 34(4): 77-80.
[本刊相关文献链接]
陈旭,王伊卿,孙琨,等.高速列车车厢夹层板断面结构的多目标优化.2013,47(1):62-67.[doi:10.7652/xjtuxb201301013]
郭空明,江俊.采用Kagome夹心板的航天器仪器安装板振动控制.2012,46(7):128-134.[doi:10.7652/xjtuxb201207023]
谷伟,张虎,李增耀,等.混合气体在典型多孔介质内扩散过程的数值模拟.2012,46(3):107-112.[doi:10.7652/xjtuxb 201203019]
张钱城,韩云杰,卢天健.超轻X型点阵芯体金属夹层板的剪切疲劳机制.2010,44(11):61-65.[doi:10.7652/xjtuxb 201011013]
张虎,谷伟,李增耀,等.氧化硅纳米多孔材料表面的水蒸气吸附动力学研究.2012,46(3):1-8.[doi:10.7652/xjtuxb 201203001]
郝星,贺健康,高琨,等.蚕丝蛋白/明胶多孔肝组织支架的制备及性能研究.2011,45(11):121-126.[doi:10.7652/xjtuxb 201111023]
于雪梅.气体静压轴承用多孔SiC陶瓷的制备及静态性能.2011,45(3):117-120.[doi:10.7652/xjtuxb201103022]
张波,陈天宁.高声压激励下多孔金属材料的吸声性能数值计算.2010,44(3):58-62.[doi:10.7652/xjtuxb201003012]
屈治国,徐治国,陶文铨,等.通孔金属泡沫中的空气自然对流传热实验研究.2009,43(1):1-4.[doi:10.7652/xjtuxb 200901001]
(编辑 葛赵青)
InnovatingConfigurationandMechanicalPropertiesoftheCoreforUltralightandPorousQuasi-HoneycombSandwichStructure
LI Xiang1,2,3,ZHOU Youhui2,TONG Guan2,YU Licheng2,LI Yang2,ZHANG Xun2
(1. Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, China Three Gorges University,Yichang, Hubei 443002, China; 2. College of Mechanical and Power Engineering, China Three Gorges University, Yichang, Hubei 443002, China; 3. Hubei Provincial Collaborative Innovation Center for New Energy Microgrid, Three Gorges University, Yichang, Hubei 443002, China)
By optimally organizing hexagons and rectangles for a unit cell structure of sandwich core, the concept of quasi-honeycomb sandwich structure was put forward to design a new type of quasi-honeycomb sandwich structure. Following Gibson’s unit cell theory, the mechanical equivalent model of the quasihoneycomb sandwich structure is established and the corresponding equivalent elastic constant formula is deduced. Taking a sandwich panel in a satellite structure as an example, the equivalent mechanical constants of the quasihoneycomb structure are calculated and compared with those of the hexagonal honeycomb sandwich structure, and the results show that the equivalent elastic moduli of the two structures are approximately equal, but the quasihoneycomb sandwich structure is endowed with higher equivalent shear modulus and lower equivalent body density, thus the total structure mass can be effectively reduced. Simulation verifies the correctness of the proposed mechanical equivalent model of the quasihoneycomb sandwich structure.
sandwich structure; quasi-honeycomb; equivalent elastic constant; mechanical property
2013-11-04。
李响(1979—),男,博士,讲师。
国家自然科学基金资助项目(51305232);湖北省自然科学基金资助项目(2013CFB222);水电机械设备设计与维护湖北省重点实验室开放基金资助项目(2012KJX07);三峡大学博士科研启动基金资助项目(KJ2012B015);三峡大学“求索”大学生创新活动计划重点资助项目。
时间:2014-04-18
10.7652/xjtuxb201409015
TB333
:A
:0253-987X(2014)09-0088-07
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140418.1749.002.html

