约束阻尼结构的振动分析及结构参数优化研究

舒歌群,赵文龙,梁兴雨,陈宇,孙秀秀

(天津大学内燃机燃烧学国家重点实验室, 300072, 天津)

约束阻尼结构的振动分析及结构参数优化研究

舒歌群,赵文龙,梁兴雨,陈宇,孙秀秀

(天津大学内燃机燃烧学国家重点实验室, 300072, 天津)

为了准确获取约束阻尼复合结构(CLD)的振动特性,依据模态应变能(MSE)理论,针对黏弹性材料的温变和频变特性,基于大型通用有限元软件ANSYS及MATLAB进行了联合仿真,研究了CLD矩形薄板的振动特性。通过分析环境温度和阻尼层厚度等设计参数对结构固有频率和模态损耗因子的影响,建立了CLD设计参数的多目标优化模型,利用遗传优化算法对CLD结构参数进行了优化。分析结果表明:随着温度的升高,CLD结构的固有频率下降并趋于稳定;存在最佳温度点,使得CLD结构的模态损耗因子最大;在固有频率改变较小的情况下,通过结构参数的优化能够保证CLD结构具有低成本、高模态损耗因子等特性;联合仿真方法适用于阻尼复合结构振动特性研究,在阻尼减振技术中具有一定的理论和实用意义。

约束阻尼复合结构;黏弹性材料;固有频率;损耗因子;遗传算法

薄壁件作为发动机的重要组成结构,如油底壳、气门室罩盖等,受到激励后很容易产生振动,进而成为重要的噪声辐射源[1]。黏弹性材料具有良好的阻尼特性,通过合理的阻尼结构设计及优化,能够在较宽的频带内抑制薄壁结构的振动和噪声,因此被广泛应用于阻尼减振技术[2-6]。

自由阻尼结构(FLD)是将一定厚度的黏弹性材料涂敷于结构件表面,通过阻尼层的拉压变形来耗损振动能量,其工艺简单、成本低、优化设计方便,但对低频结构的减振降噪效果较差。约束阻尼结构(CLD)是在自由阻尼处理层外表面再粘贴一弹性层,主要通过阻尼层的剪切变形来耗损振动能量。大量计算表明,拉伸耗能远小于剪切耗能,因此约束阻尼结构的减振降噪效果优于自由阻尼结构[7]。

由于黏弹性结构振动方程的求解涉及复数域内的高阶非线性方程组问题,因此对复杂阻尼结构的计算与优化还存在很多难点。针对阻尼结构振动特性的研究,国内外学者做了大量的研究。Johnson等介绍了一种将黏弹性阻尼材料引起的结构振动复特征值问题简化为实特征值问题的分析方法——模态应变能法(MSE),结合变形能分析来确定结构的模态损耗因子[8]。Alvelidy应用MATLAB程序,通过目标函数的最速下降法对矩形板约束阻尼处理(PCLD)的位置及形状进行了优化,并取得了良好的减振效果[9]。任志刚等在考虑黏弹性材料频变特性的情况下,通过有限元程序NASTRAN、采用模态应变能迭代法求解了复合夹层梁的各阶频率及损耗因子[10]。郑成龙等基于黏弹性层的厚度和部分材料参数的随机性分析,对CLD矩形板的振动特性进行了研究[11]。

尽管模态应变能法能够采用实特征向量替代复特征向量来计算模态阻尼,以减少计算量,但黏弹性阻尼材料的温变和频变特性使得阻尼复合结构模态损耗因子的计算结果误差较大。本文根据模态应变能理论,运用有限元软件ANSYS/APDL建立了CLD矩形薄板的有限元模型,通过MATLAB调用ANSYS/APDL进行了联合仿真,以研究黏弹性材料的温变、频变特性及结构设计参数对CLD结构振动特性的影响规律,并利用遗传优化算法进行了优化设计。

1 阻尼复合结构有限元建模

模态应变能法通过阻尼层耗能与结构变形能的比值来确定阻尼复合结构的损耗因子[12]。

阻尼复合结构的总模态应变能

(1)

式中:[K]为复合结构的刚度矩阵;[K]b、[K]V分别为基础金属层的单元刚度矩阵、阻尼层单元刚度矩阵,二者共同组成[K];{Φ}为阻尼复合结构的实模态向量。

一个振动周期内阻尼材料耗损的能量以热的形式散失,可表示为

(2)

式中:βV为阻尼材料的损耗因子。

复合结构的模态损耗因子η为阻尼耗散能与结构总弹性应变能之比,可表征阻尼层耗散振动能量的能力,表达式为

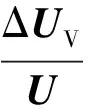
(3)

温度和频率对阻尼材料的弹性模量E′和损耗因子均有影响。为了准确预测阻尼复合结构的动力学响应和优化结构的性能,黏弹性材料对频率和温度的依赖特性必须加以考虑。利用温度和频率对黏弹性阻尼材料性能具有相反影响的关系,即阻尼材料的低温影响与高频影响等效,而高温影响与低频影响等效,可以将温度和频率综合为一个参数,即

FR=fαT

(4)

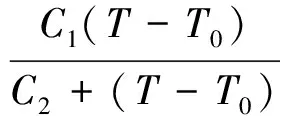
(5)

式中:FR为等效频率;αT为温频转换系数,是温度T的函数;C1、C2均为与材料相关的特性常数。则有

E′(f,T)=E′(FR)

β(f,T)=β(FR)

(6)

式中:f为实际频率。

本文选取无锡减振器厂生产的3101型黏弹性高阻尼材料作为约束阻尼复合结构的夹层材料,3101型阻尼材料特性数据的拟合函数如下[7]

(7)

(8)

(9)

材料在T0=8 ℃时的拟合结果如图1所示。由图1可知,该拟合函数可以应用于阻尼复合结构的振动分析,对阻尼减振结构进行计算及优化设计。

图1 3101型阻尼材料特性数据拟合结果

通过ANSYS的参数化程序设计语言APDL编程[13],联合MATLAB对CLD结构进行了建模和求解。

CLD结构的有限元模型:[0.5m×0.3 m],基层和约束层为铝板,阻尼层为无锡减振器厂生产的3101型阻尼材料,材料特性由式(7)、(8)获得,约束条件为四边简支。CLD结构如图2所示,具体结构的物理参数见表1。

表1 CLD结构的物理参数

以往研究表明,当弹性模量和损耗因子随频率或温度变化时,黏弹性材料的阻尼特性很难用有限元程序来描述,且动力学问题的数值计算也比较繁琐。所以,本文采用ANSYS和MATLAB联合仿真下的模态应变能迭代法来求解CLD结构的固有频率及损耗因子,计算流程如图3所示。

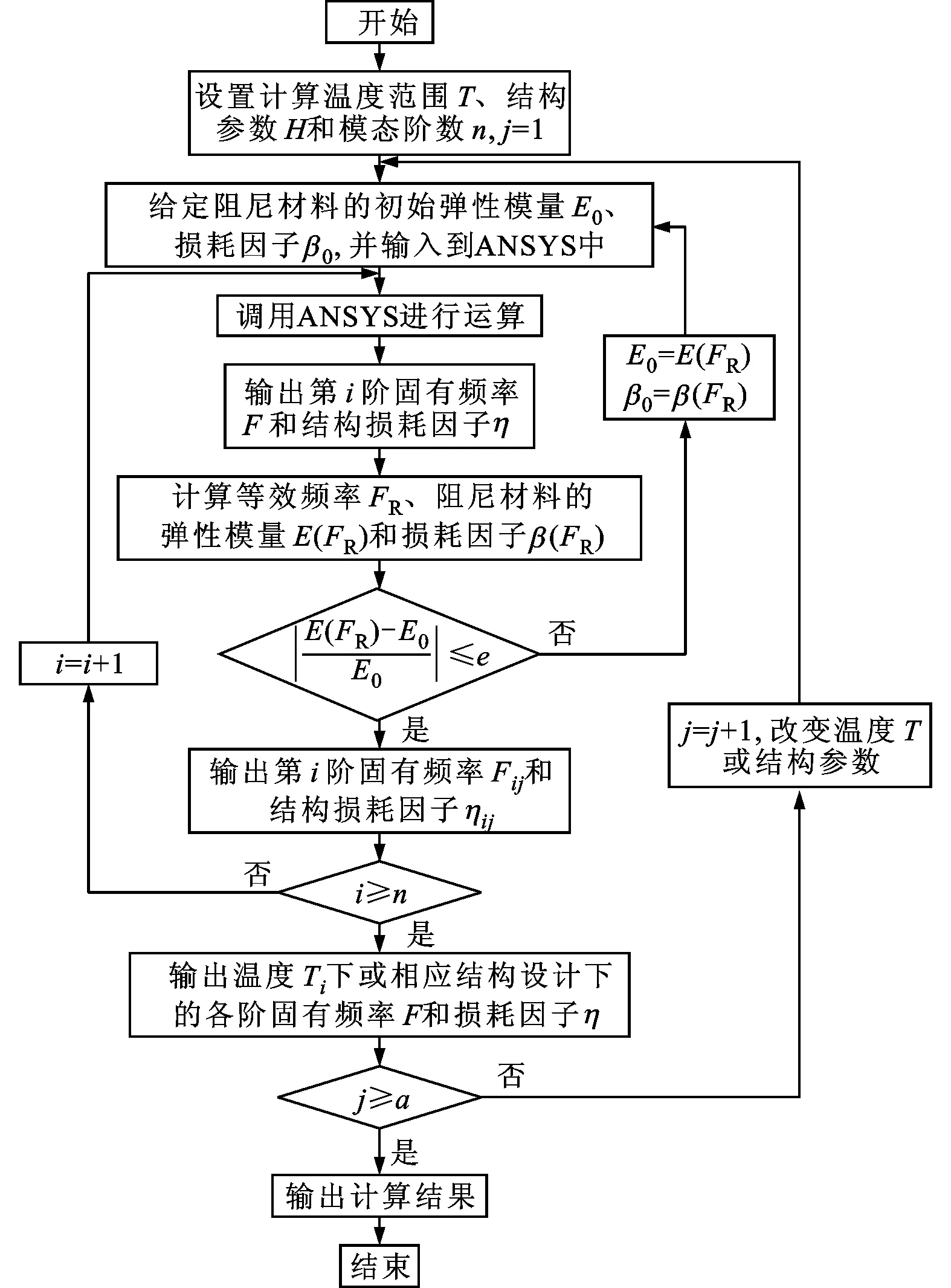
图3 CLD结构的固有频率及损耗因子迭代计算流程

2 温度和厚度参数对阻尼结构振动特性的影响

2.1 温度对CLD结构的损耗因子及固有频率的影响

由于温度影响着阻尼材料的弹性模量和损耗因子,因此工作温度成为影响阻尼结构减振降噪效果的重要参数。

CLD矩形板的模态损耗因子与温度的关系如图4所示。由图4可知,20～45℃为最佳的工作温度范围,Topt≈35℃时CLD结构的模态损耗因子最大。因此,在进行阻尼处理时尽量保证CLD矩形板最大损耗因子ηmax所对应的最佳温度相一致。此外,随着模态阶数的增加,结构的模态损耗因子增大,但高阶模态下结构的损耗因子基本不变。

图4 CLD矩形板的模态损耗因子与温度的关系

CLD矩形板的固有频率与温度的关系如图5所示。由图5可知:低温时结构的固有频率较高,随着温度的升高,固有频率降低,高温时趋于稳定;在20～50 ℃温度范围内固有频率降低的斜率最大,对应的模态损耗因子也比较大。

图5 CLD矩形板的固有频率与温度的关系

CLD矩形板固有频率是结构尺寸、材料弹性模量等参数的函数,阻尼材料的弹性模量是温度和频率的函数。

阻尼材料弹性模量随温度的升高而下降,由此导致结构刚度降低,固有频率减小。基层厚度H1和约束层H3均为2 mm时,不同阻尼层厚度H2下CLD矩形板的1阶固有频率随温度的变化如图6所示。由图6可知:低温时阻尼材料的弹性模量高,结构刚度随着阻尼层厚度的增加而增大,固有频率随之上升;高温时阻尼材料的弹性模量急剧下降且逐渐趋于稳定,阻尼层厚度增加,结构质量增大,结构刚度增大,但结构质量增大的作用会抵消结构刚度增大的作用,因此固有频率随阻尼层厚度的增加而下降并逐渐趋于平缓。对于不同阶数的振动模态,CLD结构固有频率的变化趋势与1阶模态一致。

图6 不同阻尼层厚度下CLD矩形板的1阶固有频率随温度的变化

不同阻尼层厚度下CLD矩形板的1阶模态损耗因子随温度的变化如图7所示。由图7可知,各阻尼层厚度下都存在着最佳温度点,对应着CLD结构的最大损耗因子。剪切耗能随着阻尼层厚度的增加而升高,最大损耗因子随之增大,而在转变区域以外的温度范围内,结构损耗因子变化较小,阻尼层厚度增加并未给CLD结构带来显著的阻尼效果。

图7 不同阻尼层厚度下CLD矩形板的1阶模态损耗因子随温度的变化

从图7还可知,结构的最大损耗因子所对应的温度随着阻尼材料厚度的增加发生了微小的变化。这是由于阻尼材料的损耗因子是等效频率的函数,最佳等效频率下材料的损耗因子最大,而等效频率又是固有频率和温度的函数,当温度范围为20～50 ℃时,阻尼层厚度对结构固有频率的影响减弱,固有频率基本保持不变,因此材料损耗因子最大值对应的温度也基本不变,所以CLD结构模态损耗因子对应的最佳温度随阻尼层厚度的变化比较小。

2.2 阻尼层和约束层厚度对CLD结构损耗因子及固有频率的影响

CLD结构设计主要包括结构层数、结构形式、层的厚度及材料等。根据上述分析,阻尼层厚度不同,T≈35℃时,矩形板阻尼结构损耗因子最大,所以本文仅考虑该温度下阻尼层和约束层厚度对CLD矩形板1阶固有频率和模态损耗因子的影响。基层的厚度不变,即H1=2 mm,定义阻尼层厚度比为h2=H2/H1,约束层厚度比为h3=H3/H1。

矩形板1阶模态损耗因子最大值与h2、h3的关系如图8所示。由图8可知:当h2<1时,1阶模态损耗因子随h2的增加而增大,但h3越大,1阶模态损耗因子增加越缓;当h2>1时,1阶模态损耗因子增加的幅度减小并逐渐趋于稳定;h3变化时存在最佳值h3≈1;当h3<1时,1阶模态损耗因子随h3的增加而单调上升。不同阶次下结构的模态损耗因子随阻尼层和约束层厚度的变化关系与1阶模态趋于一致,因此本文不再赘述。

固有频率与h2、h3的关系如图9所示。由图9可知,增加阻尼层厚度会降低CLD矩形板的固有频率。这是由于阻尼层黏弹性材料的弹性模量较低时,随着h2的增加,剪切变形引起的阻尼结构弯曲刚度下降,整个结构变“软”,所以固有频率降低。当h2>1时,结构的固有频率基本不变甚至略微升高。这是由于阻尼层厚度增加,结构的质量增大,各层的几何中心和复合结构的实际弯曲中心(中性层)偏移导致结构的弯曲刚度增大,使得固有频率不变甚至具有升高的趋势。由图9还可知,随着h3的增加,CLD矩形板的固有频率逐渐升高,且变化趋势在h3>1时增大。

(a)与阻尼层厚度比的关系

(b)与约束层厚度比的关系

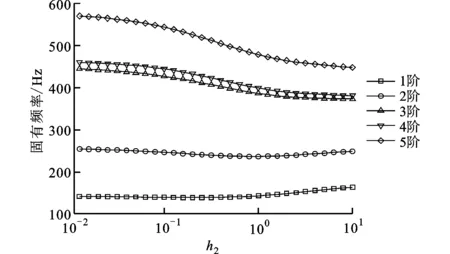
(a)与阻尼层厚度比的关系

(b)与约束层厚度比的关系

3 约束阻尼复合结构的动力学优化

为了满足结构动态特性与阻尼减振的要求,阻尼结构必须进行优化设计。

以CLD矩形板各阶的模态损耗因子最大、固有频率降低量最小、阻尼处理附加质量最小为优化目标,采用权重系数法将多目标优化函数转变为单目标函数进行最优求解。CLD结构多目标优化设计模型如下[14]

(10)

式中:ai和bi分别为CLD结构的第i阶模态损耗因子和固有频率的权重系数;c为CLD结构附加质量的权重系数;f0i为参考结构的第i阶固有频率;η0i为参考结构的模态损耗因子(引入f0i和η0i的目的是使优化目标函数无量纲化);M0为参考结构的质量。

通过上述讨论,本文选择T=35℃、H1=2 mm、H2=1 mm、H3=2 mm,采用MATLAB提供的遗传算法对CLD矩形板进行优化。计算中遗传算法的种群数为20,交叉概率为0.8,变异概率为0.2,最大进化代数为25。为了简单起见,目标优化函数中仅考虑前2阶模态,即f0i=[140.6,238.2],η0i=[0.127,0.158]。优化结果如表2所示。

表2 CLD结构动力学优化结果

注:M为阻尼处理后结构的质量。

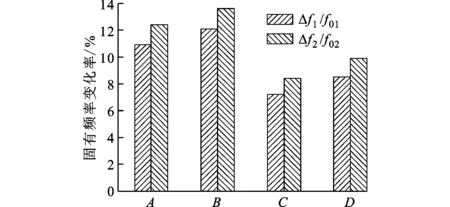
不同权重系数下参数优化设计结果对比如图10所示。优化方案A、B中优化目标函数不含模态频率权重系数bi时,相比优化方案C、D,阻尼层厚度较大,约束层厚度较小,优化后结构的损耗因子(见图10b)相对于参考结构的改变量(增加量)(η1-η01)/η01比较大,固有频率(见图10c)的改变量(降低量)|fi-f0i|/f0i也比较大。方案A、C中优化目标函数不含CLD结构附加质量的权重系数c时,相比方案B、D,优化后结构的质量较大,但比参考结构的质量小,优化后结构的损耗因子和固有频率变化较小。综上所述,b=[1,1]是影响较大的权重系数,综合各因素知,方案D可为最优配置。

(a)结构参数

(b)损耗因子

(c)固有频率

4 结 论

通过ANSYS与MATLAB的联合仿真,应用模态应变能迭代法,考虑黏弹性材料的温变和频变特性,研究了环境温度和结构设计参数对约束阻尼结构固有频率和模态损耗因子的影响,结论如下。

(1)对于特定的CLD结构,存在最佳的工作温度可使得结构的模态损耗因子最大;模态损耗因子随阻尼层厚度比的增大而增加,而结构固有频率变化较平缓;结构的固有频率随约束层厚度比增大而增大,存在最佳值h3≈1使得阻尼结构模态损耗因子最大。

(2)采用遗传算法对CLD结构进行参数优化设计,既能保证CLD结构具有较高的模态损耗因子和较好的减振降噪效果,又能降低阻尼结构的质量及成本。

(3)应用ANSYS和MATLAB联合仿真的方法能够灵活地对阻尼复合结构振动特性进行研究,在黏弹性阻尼结构的设计和优化中具有良好的可操作性和实用性,在内燃机薄壁件阻尼减振方面具有一定的理论和实用意义。

[1] 向建华, 廖日东, 蒲大宇, 等.内燃机薄板箱体部分覆盖阻尼层技术研究 [J].北京理工大学学报, 2010, 30(2): 149-153.XIANG Jianhua, LIAO Ridong, PU Dayu, et al.A study on partial coating damping layer for thin-wall box of internal combustion engine [J].Transactions of Beijing Institute of Technology, 2010, 30(2): 149-153.

[2] RAO M D.Recent applications of viscoelastic damping for noise control in automobiles and commercial airplanes [J].Journal of Sound and Vibration, 2003, 262(3): 457-474.

[3] SUBRAMANIAN S, SURAMPUDI R, THOMSON K R, et al.Optimization of damping treatment for structure borne noise reduction [J].SAE Transactions, 2003, 112(6): 1926-1938.

[4] DA SILVA I.The use of a simply vibration analysis method for optimization of vibration damping material in vehicle panels, 2010-36-0396 [R].Washington DC, USA: SAE, 2010.

[5] 梁兴雨, 舒歌群.内燃机阻尼薄壁件减振降噪机理分析 [J].内燃机学报, 2008, 26(3): 259-263.LIANG Xingyu, SHU Gequn.Analysis on vibration and noise reduction mechanism of thin-wall damping parts [J].Transactions of CSICE, 2008, 26(3): 259-263.

[6] 刘献栋, 张永仁, 何田, 等.阻尼材料在油底壳减振降噪中的应用研究 [J].噪声与振动控制, 2008, 28(1): 132-137.LIU Xiandong, ZHANG Yongren, HE Tian, et al.Application of damping materials in oil-pan’s vibration and noise control [J].Noise and Vibration Control, 2008, 28(1): 132-137.

[7] 孙庆鸿, 张启军, 姚慧珠.振动与噪声的阻尼控制 [M].北京: 机械工业出版社.1993.

[8] JOHNSON C D, KIENHOLZ D A.Finite element prediction of damping in structures with constrained viscoelastic layers [J].AIAA Journal, 1982, 20(9): 1284-1290.

[9] ALVELID M.Optimal position and shape of applied damping material [J].Journal of Sound and Vibration, 2008, 310(4/5): 947-965.

[10]任志刚, 卢哲安, 楼梦麟.复合夹层结构频率及损耗因子的计算 [J].地震工程与工程振动, 2004, 24(2): 101-106.REN Zhigang, LU Zhe’an, LOU Menglin.Calculation of frequency and loss factor of composite sandwich

structures [J].Earthquake Engineering and Engineering Vibration, 2004, 24(2): 101-106.

[11]郑成龙, 张志勇, 周长江.考虑参数随机性的约束阻尼结构振动特性分析 [J].噪声与振动控制, 2012(5): 49-52.ZHENG Chenglong, ZHANG Zhiyong, ZHOU Changjiang.Study on vibration characteristics of constrained damping structure with considering of parameter randomness [J].Noise and Vibration Control, 2012(5): 49-52.

[12]梁新华.汽车车身薄壁件阻尼复合结构振动——声学分析与优化 [D].上海: 上海交通大学, 2007.

[13]张敬莹.粘弹性夹层板振动特性的有限元分析 [D].大连: 大连理工大学, 2007.

[14]CHEN Y, HUANG S.An optimal placement of CLD treatment for vibration suppression of plates [J].International Journal of Mechanical Sciences, 2002, 44(8): 1801-1821.

(编辑 苗凌)

VibrationAnalysisandOptimizationofCompositeStructurewithConstrained-LayerDampingTreatment

SHU Gequn,ZHAO Wenlong,LIANG Xingyu,CHEN Yu,SUN Xiuxiu

(State Key Laboratory of Engines, Tianjin University, Tianjin 300072, China)

A study on structure parameters of constrained-layer damping (CLD) plates was conducted to accurately calculate the vibration characteristics of the CLD structure.The modal strain energy (MSE) iteration method was applied to construct the finite element model of CLD, and co-simulation of ANSYS and MATLAB was adopted to calculate the natural frequencies and loss factors of a rectangular plate with CLD treatment.The effect of environmental temperature and structural parameters on natural frequency and modal loss factors of the CLD plate was analyzed.The multi-objective optimization model of CLD design parameters was established with genetic algorithm (GA).The calculation results show that the natural frequency declines and tends to be stable at a certain value with an increase in the environmental temperature.There is also an optimum temperature at which the loss factor of the plate is maximum.The structural parameters optimization can ensure the characteristics of low-cost, high loss factor for CLD structure with small change of natural frequency.It seems that the co-simulation method is feasible in the vibration characteristics analysis.

constrained layer damping; viscoelastic material; natural frequency; loss factor; genetic algorithm

10.7652/xjtuxb201403020

2013-05-02。

舒歌群(1964—),男,博士,教授。

国家高技术研究发展计划资助项目

时间: 2013-12-19

O32;TH113.1

:A

:0253-987X(2014)03-0108-07

(2012AA111702)。

网络出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20131219.1121.005.html