用于三维非均质流场计算的改进流线迎风Petrov-Galerkin(SUPG)方法

苏波,韩向科

(1.江苏大学土木工程与力学学院, 212013, 江苏镇江; 2.中冶天工上海十三冶建设有限公司, 200092, 上海)

用于三维非均质流场计算的改进流线迎风Petrov-Galerkin(SUPG)方法

苏波1,韩向科2

(1.江苏大学土木工程与力学学院, 212013, 江苏镇江; 2.中冶天工上海十三冶建设有限公司, 200092, 上海)

在流线迎风Petrov-Galerkin(SUPG)稳定有限元方法基础上,通过引入双时间步法和变量分裂算法,发展了一种可用于三维非均质流场计算的改进SUPG方法。该方法摒弃了传统不可压缩流动问题中密度为常数的假定,采用包含密度输运方程的流体运动控制方程;基于变量分裂算法,速度、压强场采用同阶插值函数进行空间离散,使改进SUPG方法具有简明的有限元格式,同时对速度场、压强场进行迭代求解,以降低线性代数方程组的阶数。双时间步法的引入,有利于提高SUPG方法对复杂非定常问题的求解效率。采用该方法对非均质、非定常三维矩形管道重力作用下的自由流动问题进行了分析,研究了重力作用下两种不同密度液体的相对运动过程。计算分析表明:在采用较大时间步的情况下,速度场和压强场在整个流动过程中随时间平稳过渡且分布光滑,没有出现数值波动现象;旋涡位置及其随时间变化的规律与经典文献结果相符,没有出现跳跃和不连续现象。算例分析表明,改进SUPG方法具有良好的计算精度及数值稳定性,可用于三维非均质流动类似问题的研究。

不可压流动;有限元法;分裂算法;流线迎风

有限元方法由于可采用非结构网格、易处理复杂边界条件等优点,近些年来在工程问题中的流体计算领域得到了广泛研究和重视[1-5]。但是,当对流项占优时,采用经典Garlerkin法求解流体N-S方程会引起数值波动。Brooks和Hughes针对定常对流扩散问题,提出了流线迎风Petrov-Galerkin(SUPG)方法,有效地解决了对流项引起的数值波动问题[6]。Jameson提出了双时间步法,在计算精度和计算效率上具有较高的优越性,适合定常、非定常问题的求解[7]。此外,对于黏性不可压流动问题,通过变量分裂法[8]将速度场和压强场解耦,直接避免了LBB(Ladyzhenskaya-Babǔska-Brezzi)条件的限制,可以使单元速度、压强采用同阶插值函数,易于对混合场进行有限元空间离散。

在对黏性不可压流动问题进行有限元求解时,通常假定密度为常数[2,9],即采用均质流场进行求解。这样虽然简化了黏性不可压流动问题的计算过程,但同时给问题的分析带来局限性。为能对非均质流场进行精确分析,本文摒弃了密度为常数的假定,采用原始黏性不可压流体运动控制方程,继而综合运用上述各种数值方法,提出一种适用于非定常黏性不可压流动问题求解的改进SUPG有限元方法,并给出相应的有限元计算步骤和格式。最后,对三维管道中变密度液体在重力作用下的自由流动问题进行分析,以验证该方法的有效性。

1 不可压流体运动控制方程

一般流体运动的连续性方程为

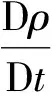
(1)

对于黏性不可压流体,根据定义,流体的密度ρ在运动过程中保持不变,即

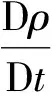
(2)

当假定密度ρ为常数时,式(2)自动满足,质量守恒仅需满足速度散度为0的条件。但是,对于非均匀流场,式(2)中隐含了密度场运动条件,是不可忽略的,因此,对于非均质黏性不可压流体,其运动控制方程为

(3)

(4)

(5)

式中:ρ为流体密度;Vi为流体速度分量;xi为直角坐标分量;t为时间。式(3)、式(5)可简写为

(6)

(7)

式中

2 控制方程的双时间步离散

对式(6)、式(7)采用双时间步法[7]进行求解

(8)

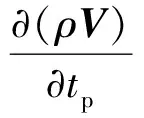
(9)

对式(8)、式(9)中关于虚拟时间tp的导数项采用加权隐格式[10]进行时间离散,关于物理时间的导数项采用二阶精度三点向后差分格式,得

(10)

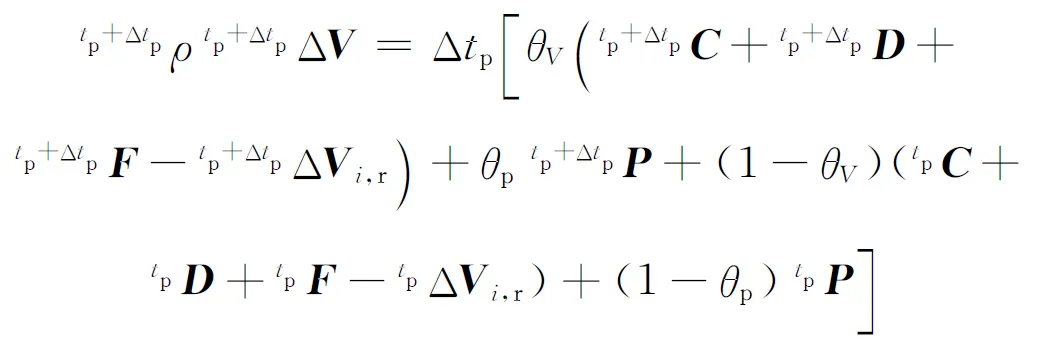
(11)

式中

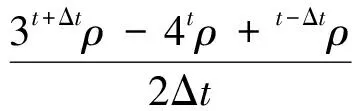
(12)

(13)

上角标t表示物理时刻t的已知变量;tp表示虚拟时刻tp的已知变量;t+Δt表示物理时刻t+Δt的待求变量;tp+Δtp表示虚拟时刻tp+Δtp的待求变量;Δt为物理时间步长;Δtp为虚拟时间步长;tp+ΔtpΔρ为虚拟时间的密度增量,tp+ΔtpΔρ=tp+Δtpρ-tpρ;tp+ΔtpΔV为虚拟时间的速度增量,tp+ΔtpΔV=tp+ΔtpV-tpV;θρ、θV、θp为时间离散权系数。

3 求解流体运动控制方程的变量分裂法

采用变量分裂算法[8],对式(10)、式(11)方程组的速度场、压强场进行迭代求解,计算步骤如下:

第1步,由式(10)求出时刻tp+Δtp的密度增量tp+ΔtpΔρ及密度全量tp+Δtpρ=tpρ+tp+ΔtpΔρ;

第2步,不考虑压强项及ΔVi,r项,计算中间速度增量

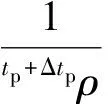
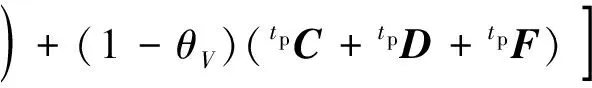
(14)

第3步,将中间速度增量tp+ΔtpΔVint及密度全量tp+Δtpρ代入下式,求解压强tp+Δtpp

(15)

第4步,根据tp+ΔtpΔVint和tp+θpΔtpp,求解速度增量

tp+ΔtpΔV=tp+ΔtpΔVint-

(16)

式(10)、式(14)～(16)即构成了基于变量分裂方法的非定常不可压流体运动的基本方程。当流场为均质流体,即密度不随空间改变时,连续性方程(3)自动满足,则上述方法退化为一般不可压流动分裂算法。

4 基于SUPG方法的不可压流动稳定有限元格式

对式(10)采用SUPG方法[1,6]进行空间离散,得到连续性方程的有限元格式

mρtp+ΔtpΔρe=rρ

(17)

式中

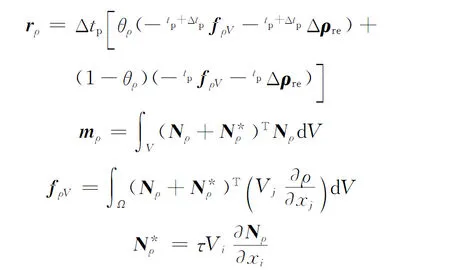
(18)

对式(14)采用SUPG有限元格式进行空间离散,得到辅助动量方程有限元格式

(19)

式中

(20)

方程组(15)可简写为泊松型压强方程[11],采用标准Galerkin有限元格式离散,得到计算压强的有限元格式的弱形式

Δtphtp+ΔtpΔpe=rp

(21)

式中

(22)

rp=θp(tp+Δtpgp-Δtphtp+Δtppe-tp+Δtpfρ)+

(1-θp)(tpgp-Δtphtppe-tpfρ)

(23)

其中

对速度修正方程,式(16)采用标准Galerkin有限元格式离散,有限元格式为

(24)

(25)

式(17)、(19)、(21)、(24)即构成了可用于非均质流场计算的改进SUPG稳定有限元格式。

5 非均质、非定常三维矩形管道重力作用下的自由流动问题

5.1 计算模型

在非均质流动算例中,双层流体在重力作用下的自由流动问题[12]是一个十分典型的算例。如图1所示,有一矩形流场,流场内盛有2种不同密度的流体,密度分别为ρ1和ρ2,且ρ2>ρ1,密度较大的流体位于流场上部,密度较小的流体位于流场下部。参考二维算例[13],初始密度分布为

ρ(x,y,z,t=0)=

(26)

式中:η(x)=-0.1dcos(2πx/d);d为指定长度。

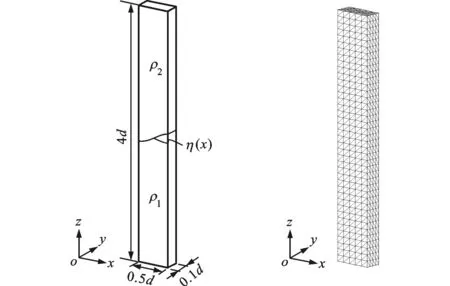
(a)流场几何尺寸 (b)有限元网格划分

有限元网格划分形式见图1b,计算雷诺数定义为Re=ρ1d3/2g1/2/μ[14],其中g为重力加速度,μ为液体的动力黏性系数。其他计算条件见表1。

表1 双层液体流动模型计算条件

在重力作用下,流场中2种液体发生相对运动。虽然流场形状简单,但随着上部液体向下流动,2种液体逐渐融合交织,导致流动状态十分复杂,流动对网格形式、边界条件等因素十分敏感,容易引起数值求解失败[13]。

5.2 结果分析

图2给出了流场在不同时刻的密度分布规律。在重力作用下,矩形流场上部密度较大的液体向下流动。当t=1 s时,2种液体分界面逐渐扩大,但流场分布规律仍和初始分布规律基本相似;当t=1.5s时,上部液体继续向下流动,且在两液体交界面处开始形成旋涡,但2种液体仍然具有较为明显的分界面;当t=1.75s时,与t=1.5s时的分布规律基本一致,2种液体交界面处旋涡更加明显;当t=2 s时,2种液体的交界面逐渐扩大,并相互交织,旋涡继续增强,旋涡中心逐渐上移;当t>2 s时,流场的流动特性开始发生改变,随着2种液体的交界面继续扩大,交界面逐渐模糊,流场中部2种液体已相互渗透,流动情况愈加复杂,这与文献[13-14]中给出的分布规律相同。

图3～图5给出了整个流动过程中的压强和速度场分布规律。如图所示,在整个时段内,尽管流动状态复杂,但压强和速度分布光滑,随时间变化过渡平稳,可以得到稳定的压强场和速度场,没有出现数值波动现象。

图6和图7分别给出了流动过程中的流线图和流场中旋涡位置随时间的变化规律。在整个流动过程中,旋涡位置在x方向变化幅度较小,在约t=1 s之前旋涡略向左侧靠拢,随后逐渐向右侧边发展;相比之下,旋涡位置在z方向变化幅度较为明显,在t=0.5s之前z向坐标值变化较为缓慢,随后迅速变小,至约1.8 s左右又逐渐增大,整体呈正弦曲线规律。图8给出了流场的上部和下部液体分界面位置随时间的变化规律,可以看出,本文的计算结果与文献[14]给出的计算结果十分吻合。

为使求解收敛,文献[14]采用的归一化时间步为Δtnon=5×10-4,文献[15]选择的归一化时间步为Δtnon=0.001 25(At)1/2=8.84×10-4,而本算例采用较大的归一化时间步:Δtnon=t(At)1/2=0.1(At)1/2=7.07×10-2。计算表明,在整个流动过程中旋涡位置变化平稳,没有出现任何跳跃和不连续现象,依然可以获得良好的计算精度,可见本文提出的改进SUPG方法在时间方向具有良好的稳定性能。

图2 密度ρ的分布规律

图3 速度Vx的分布规律

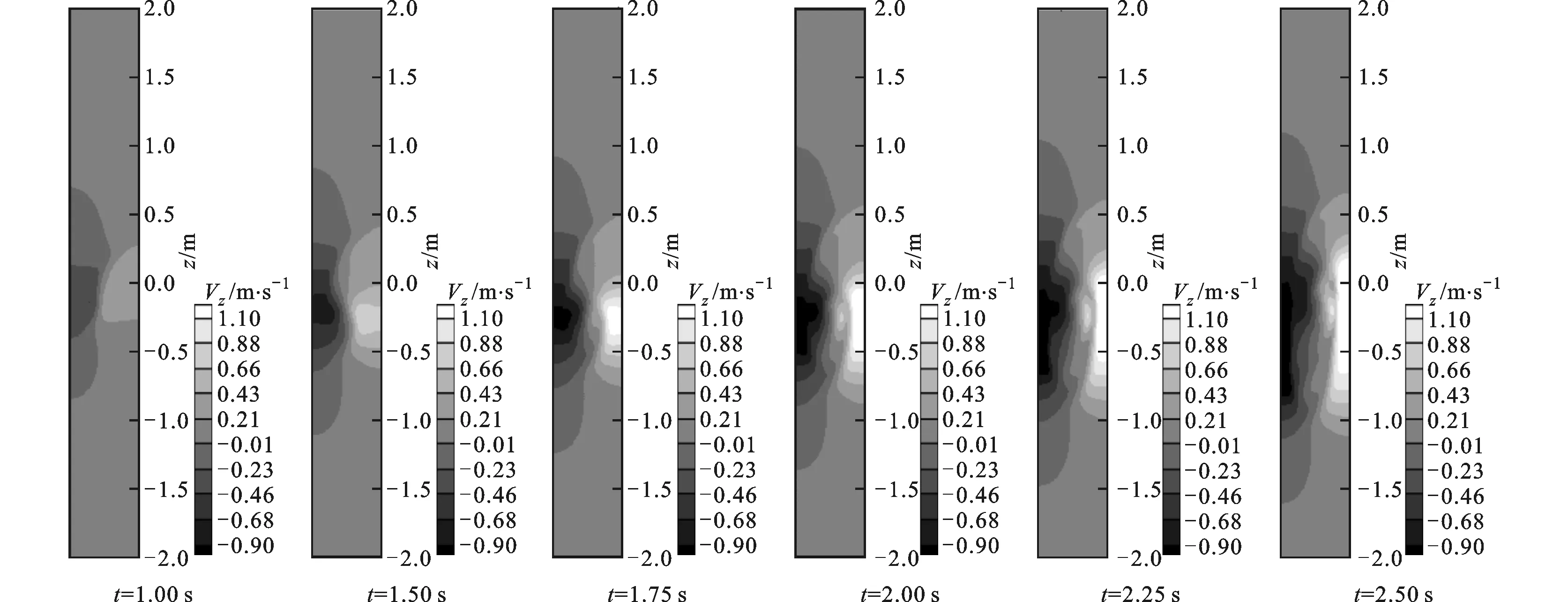
图4 速度Vz分布规律

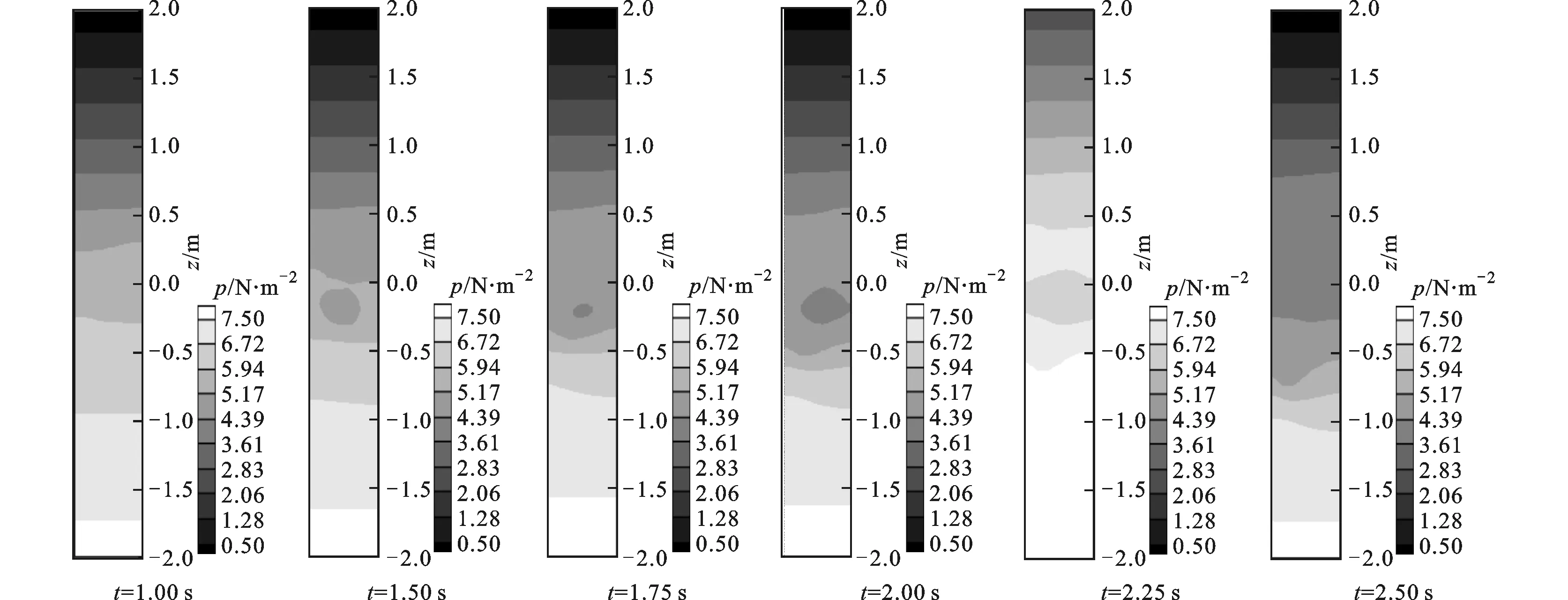
图5 压强p的分布规律

图6 y=0.05m中面流线图

图7 旋涡位置随时间的变化

图8 分界面位置随时间的变化对比

6 结 论

本文所提出的改进SUPG方法摒弃了密度为常数的假定,采用包含密度输运方程的黏性不可压流体运动控制方程组,使之可用于非均质流场的分析。由于采用变量分裂算法,速度场和压强场可采用同阶插值函数进行空间离散,使改进SUPG方法具有简明的有限元格式,并且速度场与压强场可依次求解,降低了线性代数方程组的阶数,有利于大规模问题的求解。改进SUPG方法引入双时间步法进行时间离散,有利于提高非定常问题的求解精度。算例分析表明,改进SUPG方法可对重力作用下三维矩形管道内的自由流动问题进行有效分析,得到稳定的速度场、压强场以及涡流变化规律,从而实现对非均匀、非定常等复杂流动问题的求解。

[1] HUANG Cheng, ZHOU Dai, BAO Yan, et al.A stabilized finite element technique and its application for turbulent flow with high Reynolds number [J].Wind and Structures, 2011, 14(5): 465-480.

[2] ZIENKIEWICZ O C, TAYLOR R L.The finite element method for fluid dynamics [M].5th ed.Amsterdam, The Netherlands: Elsevier, 2000.

[3] 钱若军, 董石麟, 袁行飞.流固耦合理论研究进展 [J].空间结构, 2008, 4(1): 3-15.QIAN Ruo-jun, DONG Shi-lin, YUAN Xing-fei.Advances in research on fluid-structure interaction theory [J].Spacial Structures, 2008, 4(1): 3-15.

[4] 韩向科, 苏波.黏性不可压流体的一种FCBIS三角形单元 [J].力学与实践, 2010, 32(3): 22-25.HAN Xiangke, SU Bo.A FCBIS triangular element for incompressible fluid flows [J].Mechanics in Engineering, 2010, 32(3): 22-25.

[5] KOHNO H, BATHE K J.A nine-node quadrilateral FCBI element for incompressible fluid flows [J].Communications in Numerical Methods in Engineering, 2006, 22(8): 917-931.

[6] BROOKS A N, HUGHES T J R.Streamline upwind/Petrov-Galerkin formulation for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations [J].Computer Methods in Applied Mechanics and Engineering, 1982, 32(1/2/3): 199-259.

[7] JAMESON A.Time dependent calculation using multigrid with applications to unsteady flows past airfoils and wings [C]∥Proceedings of AIAA 10th Computational Fluid Dynamics Conference.Reston, VA, USA: AIAA, 1991: 1-8.

[8] NITHIARASU P, CODINA R, ZIENKIEWICZ O C.The characteristic-based split (CBS) scheme: a unified approach to fluid dynamics [J].Numerical Methods in Engineering, 2006, 66(10): 1514-1546.

[9] ADINA R&D Inc.ADINA CFD&FSI: theory and modeling guide [M].Watertown, MA, USA: ADINA R&D Inc., 2005.

[10]DONEA J, HUERTA A.Finite element methods for flow problems [M].London, UK: John Wiley & Sons, 2003: 92-93.

[11]GRESHO P M, SANI R L.Incompressible flow and the finite element method [M].New York, USA: John Wiley & Sons, 2000: 302.

[12]TRYGGVASON G.Numerical simulation of the Rayleigh-Taylor instability [J].Journal of Computational Physics, 1988, 75(2): 253-282.

[13]CALGARO C, CREUSE E, GOUDON T.A hybrid finite volume-finite element method for variable density incompressible flows [J].Journal of Computational Physics, 2008, 227(9): 4671-4696.

[14]GUERMOND J L, QUARTAPELLE L.A projection FEM for variable density incompressible flows [J].Journal of Computational Physics, 2000, 165(1): 167-188.

[15]GUERMOND J L, SALGADO A.A splitting method for incompressible flows with variable density based on a pressure Poisson equation [J].Journal of Computational Physics, 2009, 228(8): 2834-2846.

[本刊相关文献链接]

赵立波,徐龙起,热合曼艾比布力,等.矩形微悬臂梁的流固耦合谐振频率分析.2013,47(11):60-64.[doi:10.7652/xjtuxb201311011]

何联格,左正兴,向建华.气缸盖中两相流沸腾换热热机耦合仿真分析.2013,47(7):23-28.[doi:10.7652/xjtuxb201307 005]

李连忠,牛文全,魏正英,等.微灌压力调节器调压特性流固耦合数值计算及分析.2013,47(5):131-136.[doi:10.7652/xjtuxb201305024]

何联格,左正兴,向建华.气缸盖冷却水腔内两相流动沸腾传热仿真研究.2013,47(1):21-26.[doi:10.7652/xjtuxb 201301005]

张颖莉,种道彤,刘继平,等.方管内混合对流与管壁导热耦合换热的数值模拟.2012,46(5):19-24.[doi:10.7652/xjtuxb201205004]

刘小民,王星,许运宾.运动罐体内液体晃动的双向流固耦合数值分析.2012,46(5):120-126.[doi:10.7652/xjtuxb201205021]

张慧贤,寇子明,吴娟,等.液压激波作用下管道流固耦合的动力学建模.2012,46(3):94-99.[doi:10.7652/xjtuxb201203 017]

康伟,张家忠,李凯伦.利用本征正交分解的非线性Galerkin降维方法.2011,45(11):58-62.[doi:10.7652/xjtuxb201111 011]

梅冠华,张家忠.时滞惯性流形在三维壁板颤振数值分析中的应用.2011,45(9):40-46.[doi:10.7652/xjtuxb201109008]

苏波,钱若军,韩向科.一种用于流固耦合分析的有限元网格简捷更新方法.2011,45(3):16-24.[doi:10.7652/xjtuxb 201103003]

(编辑 葛赵青)

ModifiedStreamlineUpwindPetrov-Galerkin(SUPG)StrategyforCalculationofThree-DimensionalHeterogeneousFlowProblems

SU Bo1,HAN Xiangke2

(1.Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang, Jiangsu 212013, China;2.CMTCC Shanghai Shisanye Construction Co., Ltd., Shanghai 200092, China)

By introducing the dual-time stepping method and the variable splitting algorithm, a modified SUPG strategy is developed based on the stable streamline upwind Petrov-Galerkin (SUPG) finite element method, where the traditional assumption of constant density for incompressible flow problem is abandoned and the density transportation equation is introduced into the governing equations.The velocity and pressure fields are discretized with interpolating function of the same order, thus finite element scheme of the modified SUPG strategy gets simple and clear, and the order of algebraic equations is reduced.The dual-time stepping method is also introduced to enhance calculation stability of the SUPG strategy for complex unsteady problems.A free flow with heterogeneous, unsteady field of three-dimensional rectangular pipe under gravity and the whole relative motion between two types of liquids with different density are analyzed.The calculation results indicate that the velocity and pressure fields distribute and transmit smoothly with time and no numerical wave occurs in the case of greater time steps; the vortex position and its varying regulation coincide well with the results in the classic literatures without jumps and discontinuities.Example proves the numerical stability and accuracy of the modified SUPG method.

incompressible flow; finite element method; splitting algorithm; streamline upwind Petrov-Galerkin (SUPG) method

10.7652/xjtuxb201403023

2013-08-05。

苏波(1977-),男,博士,讲师。

国家自然科学基金青年基金资助项目

(51108210);江苏省博士后基金资助项目(1301048C);国家自然科学基金专项数学天元基金资助项目(11226308)。

时间: 2013-12-25

O357.1

:A

:0253-987X(2014)03-0128-07

网络出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20131225.1702.005.html