“非指示性”教学理念下“因式分解”教学探索

●

(浙江师范大学附属永康中学 浙江永康 321300)

在数学教学中，教师与学生间的关系一直是理论思考与实践探究的热点话题之一.一个基本的共识是，教学是教与学的对话，教师和学生则是数学课堂的两大主体.但这2个主体间的关系如何处理，还需在实践中探索.

对此，浙江师范大学郑逸农教授提出了“非指示性”教学(简称“非指”教学)的理念.它既不是以教师为中心的“指示性”教学，也不是以学生为中心的“非指导性”教学，而是在教师引导下，学生自主学习的一种教学理念.在教师帮助与引导下的学生自主成长是“非指”教学的基本理念.本文是在“非指”教学理念的指导下所开展的案例式的行动研究，描述与分析了2014年3月开展的原始课和改进课.

1 “因式分解”第一次实践与分析

在第一次教学中设计了如下课堂教学环节：

1.1 实例探索，激活经验

先向学生展示一个女教工在“三八节”快乐舞步健身操比赛时的视频.视频显示其方阵由36名女教师组成，舞步动作整齐，队形变化多样.紧接着提出问题：36名女教师可以摆出怎样的方阵？

教学中要求学生独立思考后，教师请一位数学自信不足的学生向全班介绍，教师板书：36=2×18,36=3×12,36=4×9,36=6×6，回忆因数分解的概念.

1.2 简便运算，形成概念

在这一环节，逐个呈现了2个计算题：

(1)1 001×23-1 001×12；

(2)87×232-87×2×23×13+87×132.

并让学生表述解题方法，体现简便运算的方法：

87×232-87×2×23×13+87×132=

87×(23-13)2.

进一步，引导学生将上述规律用字母表示：

ab2-a×2×bc+ac2=a(b-c)2.

此时，教师引出课题：我们把一个多项式进行了分解，对比因数分解，我们可以把它称为因式分解(板书标题).

1.3 自主学习，明晰概念

要求学生自主阅读课本内容，并独立完成以下问题：

(1)观察课本中表格：

左列:把( )变形为( ),称其为( );

右列:把( )变形为( ),称其为( ).

(2)什么是因式分解？关键词是什么？

(3)整式的乘法和因式分解有何关系？

(4)完成课本上的“做一做”.

(5)判断某个代数式的变形是不是因式分解，应注意什么？

学生独立思考，在动笔中进行.之后4人小组进行交流，边交流边完善，形成小组最佳答案.教师随机抽点一个代表向全班介绍，边介绍边评判和完善，形成班级最佳答案.教师在学生边介绍时边板书：一个多项式=(整式)×(整式)×(整式).

在讲解“做一做”第1题中，让学生上黑板写出几个因式分解的例子.若有错误，则拿他们的例子讲解因式分解应注意的问题；若没有错误，则举几个易错的例子让学生判断.

1.4 例题学习，巩固概念

向学生呈现以下例题:

例1检验下列因式分解是否正确：

①x2y-xy2=xy(x-y);

②2x2-1=(2x+1)(2x-1);

③x2+3x+2=(x+1)(x+2).

并思考：

(1)利用什么来检验因式分解的正确性？

(2)由第②小题的解答，请写出一个多项式的因式分解.

(3)根据例题，归纳解题书写格式.

学生独立思考，在动笔中进行.之后教师随机抽点一个代表向全班介绍，边介绍边评判和完善，形成班级最佳答案.教师在学生边介绍时边板书，引导学生规范书写步骤.

1.5 反馈检测

为了进一步让学生明确判断因式分解正确与否的方法，并能用因式分解进行简便计算，设置了以下检测.

1.检验下列因式分解是否正确.

(1)x2+xy=x(x+y);

(2)a2-4b2=(a+b)(a-b);

(3)-x2+2x-1=-(x+1)2.

2.请对照上题(1)和(2)的式子用简便方法计算下列各题：

(1)1012-992;

(2)872+87×13.

1.6 能力拓展，应用概念

1.若x2+mx-n能分解成(x-1)(x+2)，则m=( )，n=( )；

2.993-99能被100整除吗？为什么？

学生独立思考，在动笔中进行.之后4人小组进行交流，边交流边完善，各抒己见，改正不正确的做法，形成小组最佳答案.教师随机抽点一名代表回答，让学生自主分析对错，形成班级最佳答案.

1.7 概括小结

1.把( )化成( )的形式，叫做因式分解，有时也把这一过程叫( ).

2.因式分解和整式的乘法有( )关系，因此可以用( )来检验因式分解的正确性.

3.我还会用( )来简便计算.

这节课在设计与实施过程中均强调:教师利用任务驱动学生学习，先个人独立学习，后师生讨论、交流、评价，以体现教师引导与学生自主学习间的平衡.在教学中，尽管学生的学习主体已得到较好的体现，但在以下方面仍存在问题：首先，教学前2个环节，用了9分钟时间，应作删减；其次，第3个环节中，让学生观察表格表述，结果由于表格较为复杂，学生很难理解，也表达不清楚，应换种形式提问；第三，在“反馈检测”中，让学生对照前2个题目用简便方法计算872+87×13和1012-992,学生缺少独立探索的乐趣，应删去对照的2个因式分解的例子；第四，“能力拓展”中第2小题难度较大，最好放在学生学习了因式分解的方法以后，应降低难度；第五，以填空的方式让学生来总结，总结的是教师的思路，还不如请学生各抒己见，谈谈这堂课的收获，真正做到让学生来总结.针对以上不足，笔者对本节课的教学设计进行了修改，进行第2次教学实践.

2 基于“非指”的“因式分解”第2次实践与分析

在第2次教学中，我们设计了如下教学环节：

2.1 最强大脑，谁与争锋

图1

例2一座公园建筑的示意图如图1所示，环形绿化带的外圆半径为6.35 m，内圆半径为3.65 m，则这个环形绿化带的面积是多少？

学生独立思考，教师抽点一位数学学困生问：“环形绿化带的面积能直接求吗？”

生：不能！

师：可以用什么方法求？

生：用大圆面积减去小圆面积：π×6.352-π×3.652.

师：你能用5秒钟时间计算出它的结果吗？

生：不能！

师：我能用5秒钟时间计算出它的结果！不相信？学习了今天的内容你们也可以!

(设计意图：用实际问题激起学生的学习兴趣，从而自觉地投入到本堂课的学习中.)

2.2 自主学习，认识因式分解

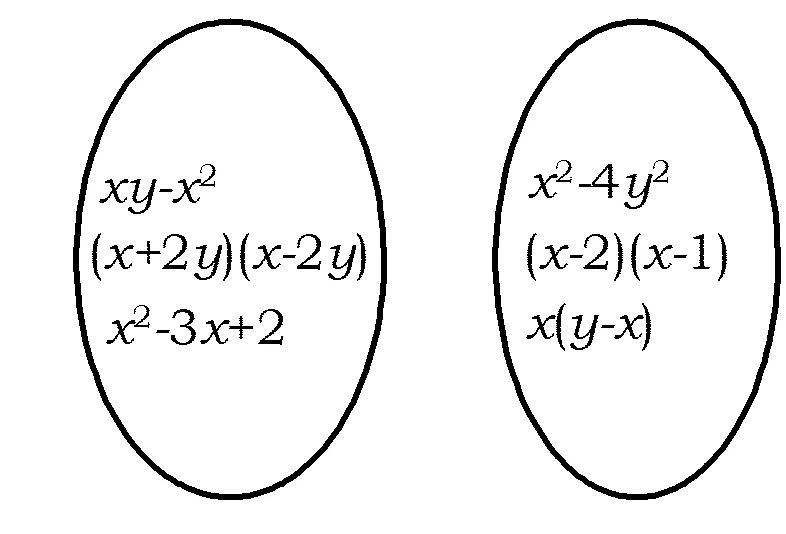
图2

完成第1次教学实践中的第3个环节(删除了其中的第1小问)，在此基础上直接给出反馈检测1：

检测1如图2，把左、右2边相等的代数式用线连接起来,并写出相应的因式分解.

学生完成后，随机抽点一位学生回答，并让不懂的学生发表自己的疑惑，给予相应的指导.

2.3 例题归纳，检验因式分解的正确性

完成第1次教学实践中的环节3，在此基础上直接给出反馈检测2:

检测2检验下列因式分解是否正确.

(1)x2+xy=x(x+y);

(2)a2-4b2=(a+b)(a-b);

(3)-x2+2x-1=-(x+1)2.

2.4 学以致用，体验因式分解的作用

1.简便运算

(1)872+87×13;

(2)1012-992.

2.一座公园建筑的示意图如图3所示，环形绿化带的外圆半径为6.35 m，内圆半径为3.65 m，则这个环形绿化带的面积是多少？

图3

2.5 总结

通过本节课的学习，你有什么收获？有什么疑问？

(设计意图：让学生自由发言交流，加深对本节课的理解.对提出的疑问，可以请其他学生发表看法或教师及时有效提示补充，这区别于传统填鸭式的教学，学生对于自己提出的问题会听得更认真，体现了郑教授的“非指”理念.)

在第2次教学实践中，对第1次课堂教学的问题进行了完善.如用“最强大脑，谁与争锋”来替换前2个环节，使教学更加简洁与有效；在“自主学习”中，直接简单明确地让学生说出因式分解的概念和关键词，避免了学生的误解；每个环节一个“反馈检测”，充分了解学生的掌握情况；“学以致用”用2个方面体验因式分解的作用，首尾呼应；总结让学生各抒己见，真正做到让学生来总结，效果较好.

通过“因式分解”的2次实际教学尝试，教师引导，学生自主学习的“非指”教学理念是有效的，而且值得推崇.在“非指”教学理念下，初中数学教学过程中，教师用任务驱动学生的学习；在每个环节中，通过反馈检测及时了解学生的掌握情况，并通过自我反思、师生交流、生生交流深化理解.

鸣谢：本课例从最初的设计到实施，再到成文都得到了浙江师范大学教师教育学院唐恒钧博士和郑逸农教授的指导，在此表示衷心的感谢！