不确定条件下的城市应急车辆调度模型研究

赵韩涛, 毛宏燕, 黄瑞锦

(1. 哈尔滨工业大学 (威海)汽车工程学院,山东 威海 264209; 2. 哈尔滨工业大学 (威海)图书馆,山东 威海 264209; 3. 哈尔滨工业大学 交通科学与工程学院,哈尔滨 150090)

不确定条件下的城市应急车辆调度模型研究

赵韩涛*, 毛宏燕2, 黄瑞锦3

(1. 哈尔滨工业大学 (威海)汽车工程学院,山东 威海 264209; 2. 哈尔滨工业大学 (威海)图书馆,山东 威海 264209; 3. 哈尔滨工业大学 交通科学与工程学院,哈尔滨 150090)

为了改善不确定条件下突发事件的响应效率,用数学规划的方法优化了城市应急车辆调度模型.针对现有调度数学模型存在着立足于当前事件而忽略防范未来事件的问题,建立了以带权重响应时间成本为目标函数的数学公式,并从时空限制的角度初步探讨了不同交通流量下的行程时间计算.案例研究结果表明:未来事件成真时,所建模型生成的调度策略减少了总体响应时间成本;置信水平的选取决定了系统对未来事件的重视程度,趋向于 1 时侧重防范未来严重事件,趋向于 0 时优先考虑当前事件.

交通工程;应急;车辆调度;不确定条件;行程时间

1 引 言

紧急救援车辆系统的设计和运作在应急响应领域中受到广泛重视.系统的首要问题是建立和求解数学模型以辅助决策.Goldberg[1]总结前人研究成果,将该领域的研究归纳为四类:车辆的选址;车辆的调度;不同类型应急单元进行组合时的车辆数量、配备的职员数及附属的装备水平;不同系统状态下资源的再分配.本文的研究属于车辆调度方面.应急条件下的车辆路径选择具有时间紧迫性、不确定性和资源有限等特点,常态下的车辆路径问题的理论和方法具有一定的局限性.

当前,国外在不确定条件下的应急研究偏向于应急单元的选址模型[2]、行程时间的经验公式[3]及有限调度资源的配置方法[4]等.车辆调度与不确定性条件相结合方面,Pal[5]强调交通条件和事件的随机性,利用仿真模型设计车辆在高速公路上的巡逻系统;Ali Haghani[6]建立了实时条件下车辆调度和路径选择的优化模型;Kaan Ozbay[7]研究了事件管理系统中车辆调度和资源配置的随机规划模型.国内在应急车辆调度模型方面的研究也开始从确定性条件转向不确定性条件.杨晓光、彭春露[8]利用模糊评价的方法构造了救援车辆通行畅通可靠度的评价模型;辜勇、严新平[9]等研究了随机行程时间条件下的车辆调度模型;杨孝宽[10]、刘杨[11,12]等从不同角度研究了应急车辆实时行程时间的计算.

本文在相关文献研究成果的基础上,以应急车辆调度为研究对象,依据当前事件信息和未来事件发生的概率,建立不确定条件下的城市车辆调度模型.

2 问题分析

应急车辆调度决策的优劣是应急系统能否成功运行的关键因素.应急车辆调度模型研究的目的是为了建立数学公式以辅助应急决策.作者在文献[13]中利用整数规划建立了以整体损失最小为目标函数的数学模型:式中 Xji(t) 为 0-1 决策变量;Tji(t) 为应急车辆响应时间;EPi为事件权重.

该模型重点考虑多起不同类型事件同时发生时的优化调度,模型中未考虑行程时间的计算.缩短应急车辆行程时间对于减少突发事件造成的直接和间接损失至关重要.应急车辆在响应过程中会拉响警报,在路段和交叉口处均具有优先通行权.因此,在车辆调度的模型研究中,对应急车辆的行程时间研究较少,一般直接取距离和平均速度的商值.然而,在现实的城市环境下,应急车辆会遭遇不同拥堵程度的路网条件,阻碍其快速响应.

另外,该模型仅针对当前的突发事件,未考虑车辆被调度之后其所辖区域再次发生事件时的防范策略.如某车辆被调度响应一个优先级别较低的事件,此时在其站点就近区域突发优先级别较高的事件,会造成该事件的响应时间延迟.

针对上述问题,本文将考虑行程时间随机变化、未来事件发生的位置随机和类型随机等不确定性因素,进一步完善应急车辆调度模型.

3 模型构建

3.1 车辆调度模型

依据上述问题分析,本部分建立以当前事件和未来事件的总体响应时间成本为目标函数的数学规划模型.定义 D为所有应急车辆的数组, Dn为第 n 处应急车辆驻守站点的车辆数组,rn为第n处站点停存车辆数,N为当前需要处理的突发事件数组,F 为未来可能发生的事件数组.为降低突发事件造成的损失,不同类型的事件应赋予不同的响应时间要求,严重的事件应优先响应.定义 W 为响应时间权重数组,EP(l) 表示 W中第 l级别优先权的权重值,EPj为当前事件 j的响应时间权重值,EPk为未来事件 k的响应时间权重值.定义 tij、 tik分别为车辆从起点到事件发生点的执行响应事件、执行防范未来事件最短行程时间.决策变量 引入两个0-1 变量 xij、 xik,xij等于 1 时表示车辆 i执行响应事件 j的任务,等于0 时表示未执行任务;xik等于1时表示车辆 i执行防范未来事件 k的任务,等于 0 时表示未执行任务.建立应急车辆调度模型如下:

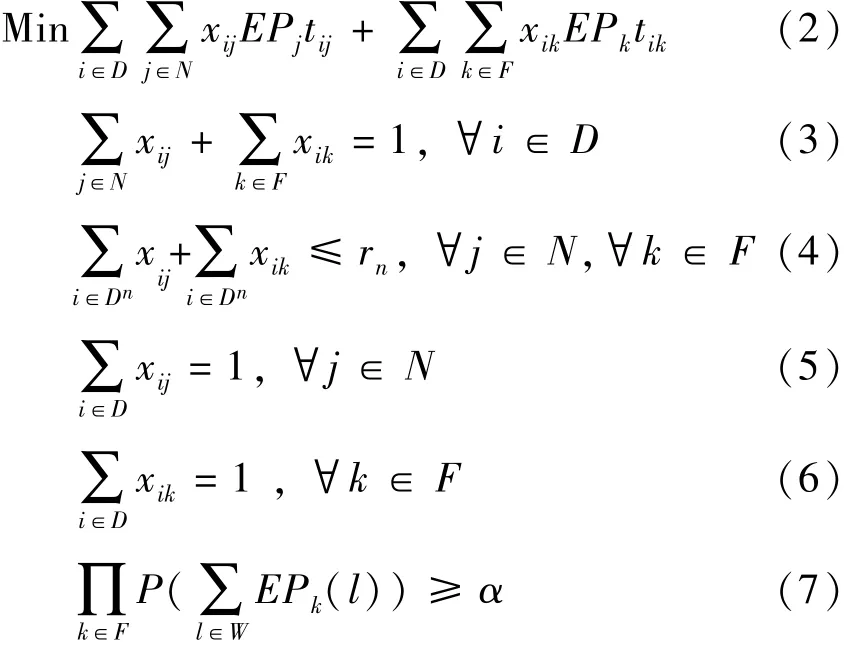
式(2)表明目标函数由当前事件的带权重响应时间成本和未来事件的带权重响应时间成本两部分组成.相比于式(1),模型中增加的后一项注重防范未来严重事件的发生.式(3)约束每辆车只能执行一项任务;式(4)表明响应事件的车辆数受限于站点的车辆数;式(5)约束当前发生的事件只有一辆车进行响应;式(6)约束未来发生的事件只有一辆车进行响应;式(7)表明系统防范未来事件的能力应达到一定的置信水平,定义为 α.

模型(2)中,应急车辆行程时间、事件的权重和置信水平α等三个参数体现了模型适用于不确定条件下的应急需求.事件的严重程度是随机的,严重的事件应优先响应.不同类型事件的权重值可采用层次分析法予以确定.α表示未来所发生的事件能够得到满意响应的概率,由区域中突发事件的概率和严重程度概率决定,需通过统计历史数据获取.下面重点探讨行程时间的确定.

3.2 行程时间模型

应急车辆通行时间,主要受两个因素影响:一是时间段,高峰期的行程时间延误明显增大;二是空间容量,道路能否提供足够的空间(包括对向车道的空间)决定了社会车流是否让行应急车辆.因此,应急车辆行程时间可基于时空限制的角度进行计算.

应急车辆的行程时间可划分为两部分:自由流阶段和延误阶段.当道路交通量达到一个临界程度(定义为 Cij) 时,社会车辆无法让行,应急车辆只能跟驰行驶,其行驶时间同社会车辆一样.

定义 Tij为应急车辆以自由流速度从 i 点到 j的行程时间,表示在 d 时刻应急车辆从 i点到 j的延误时间,L 为从 i点到 j的距离,为 d 时刻的路段交通量,v1为应急车辆自由流时的行驶速度,v2为社会车辆在 d 时刻的平均行驶速度.则应急车辆行程时间( 定义为 tij) 可描述为

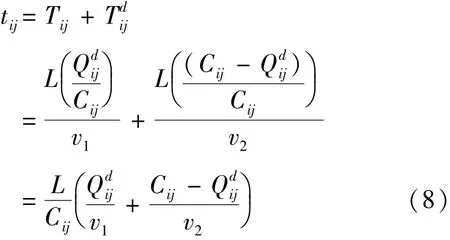
行程时间计算问题转化为临界流量 Cij的确定.对于不同区域不同等级的道路而言,临界流量值需要通过调研获取.

4 案例分析

为阐述所建立模型在突发事件管理决策中的应用,本文模拟一起突发事件案例.如图1 所示,道路网络由 16 个节点、24 条连线组成;节点 A 和 B代表应急车辆驻留站点,配备的车辆数分别为1辆和2辆;各节点之间的应急车辆行程时间为某一时间段内依据交通量得出的估计时间.

图1 道路网络示意图Fig.1 Schematic diagram of the road network

假定同时等待响应的事件位于M点和N点,其响应时间权重分别为 0.1 和 0.4;未来事件可能发生在 F 点,事件发生的概率如表1 所示,权重为0表示无事件发生.调度部门需要依据上述条件确定最优的车辆分派策略.

表1 F点突发事件的概率分布Table1 Probability distribution of emergency occurred at point F

设定未来事件被妥善响应的概率要求达到90%,根据表1的概率分布,代入式(7), 得0.9. α 取值较高,要求未来突发事件得到较高的响应权重,事件响应时间的权重值取对应的 0.3. α取 0.7,则未来事件的响应时间权重取 0.1.依据图1中所示行程时间,可计算由各车辆站点前往突发事件地点的最短行程时间,结果如表2 所示.分别采用最近距离法、模型(1)和模型(2)针对上述案例选择调度方案,结果如表3所示.

表2 响应车辆最短行程时间Table2 The shortest travel time of response vehicles

表3 不同调度方案结果对比Table3 Comparison of different scheduling scheme

由表3 可见,采用不同的调度方法,生成的调度方案各异.如果未来的事件成为现实(权重为 0. 3),则最近距离调度的带权重时间成本为 4.1,模型(1)的带权重时间成本为 3.9,模型(2)的带权重时间成本为 3.7.模型(2)降低了当前事件和未来事件的总体响应成本.

α 取值大小影响调度结果.若 α 取0,意味着不考虑未来事件的发生,模型(2)即转化为模型(1);若 α 取1,表示需要以最优的方式防范未来事件的发生,未来事件和已经发生的事件同等重要;α 取值(0,1) 之间时,决定了未来事件响应时间的权重,随着 α 的增加,车辆应倾向于防备突发严重事件的区域.

5 研究结论

考虑到未来突发事件在分布概率和严重程度方面存在着严重的不确定性,本文建立了防范未来突发事件响应需求的应急车辆调度数学规划模型.所建模型以降低当前事件和未来事件的总体响应时间成本为目标.案例研究表明,在未来突发事件成为现实时,所建模型能够降低总的响应时间成本.对比相关研究文献,本文的贡献主要有二:其一,在调度模型中引入带有权重的未来突发事件的响应时间成本,丰富了应急车辆调度问题的内容;其二,借用置信水平 α 的概念,反映整个区域内不同时间不同事件类型下应急系统达到的服务水平,同时反映了区域内各个位置突发事件的分布概率.

[1] Goldberg J B.Operations research models for the deployment of emergency services vehicles[J].EMS Management Journal,2004,1(1):20-39.

[2] Lei H,Cheu R L,Aldouri R.Optimal allocation of emergency response service units to cover critical infrastructures with time dependent service demand and travel time[C]//88th Annual Meeting of the Transportation Research Board.Washington,DC:National Research Council,2009:74-84.

[3] Budge S,Ingolfsson A,Zerom D.Empirical analysis of ambulance traveltimes: the case ofcalgary emergency medical services[J]. Management Science,2010,56(4):716-723.

[4] Huang Y,Fan Y,Cheu R L.Optimal allocation of multiple emergency service sources for critical transportation infrastructure protection[C]//TRB 86th Annual Meeting Compendium of Papers CD-ROM, Washington, DC: National Research Council, 2007:0028.

[5] Pal R,Sinha K,Simulation model for evaluating and improving effectivenessoffreeway service patrol programs[J].Journal of Transportation Engineering, 2002,128(4):355-365.

[6] Haghani A,Huijun Hu,Qiang Tian.An optimization model for real-time emergency vehicle dispatching and routing[C]//TRB 82nd Annual Meeting Compendium of PapersCD-ROM.Washington,DC:National Research Council,2003:0710.

[7] Ozbay K,Weihua Xiao,Cem Iyigun.Probabilistic programming models for response vehicle dispatching and resource allocation in traffic incident management [C]//TRB 83rd Annual Meeting Compendium of Papers CD-ROM, Washington, DC: National Research Council,2004:0014.

[8] 杨晓光,彭春露.救援车辆通行畅通可靠度模糊综合评价方法研究[J].土木工程学报,2007,40(1): 79-84.[YANG X G,PENG C L.Travel reliability evaluation of emergency vehicles based on multilevel fuzzy synthesis judgment method[J].China Clvil Engineering Journal,2007,40(1):79-84.]

[9] Gu Yong,Yan Xinping.A dispatch model of emergency vehicles based on stochastic travel time[C]//8th International Conference of Chinese Logistics and Transportation Professionals-Logistics:The Emerging Frontiers of Transportation and Development in China, Chengdu,2008:1565-1570.

[10] 杨孝宽,宫建,曹静.奥运会突发事件疏散路径动态路段行程时间[J].北京工业大学学报,2007,33 (7):702-706.[YANG X K,GONG J,CAO J. Dynamic link travel time for evacuation route in an emergency of Olympic Games[J].Journal of Beijing University of Technology,2007,33(7):702-706.]

[11] 刘杨,郑黎黎,常云涛.城市道路应急车辆路段行程时间计算模型[J].交通与计算机,2008,26(5): 30-33.[LIU Y,ZHENG L L,CHANG Y T.Travel time model of emergency vehicles on urban road[J]. Computer andCommunications,2008,26(5): 30-33.]

[12] 刘杨,沈海州,彭国雄.基于神经网络的应急车辆行程时间计算模型[J].武汉理工大学学报(交通科学与 工 程 版 ),2007,31(6):973-975.[LIU Y, SHEN H Z,PENG G X.Travel time model of emergency vehicle based on BP network[J].Journal of Wuhan University ofTechnology(Transportation Science&Engineering),2007,31(6):973-975.]

[13] 赵韩涛,王云鹏,王俊喜,等.高速公路应急车辆指挥调度优化模型[J].吉林大学学报(工学版), 2006,36(3):336-339.[ZHAO H T,WANG Y P, WANG J X,et al.Study on optimization model for freeway emergency vehicle dispatching[J].Journal of Jilin University (Engineering and Technology Edition),2006,36(3):336-339.]

Model of Emergency Vehicle Scheduling under Uncertainty

ZHAO Han-tao1,MAO Hong-yan2,HUANG Rui-jin3
(1.School of Automobile Engineering,Harbin Institute of Technology,Weihai 264209,Shandong,China; 2.Library,Harbin Institute of Technology,Weihai 264209,Shandong,China; 3.School of Transportation Science and Engineering,Harbin Institute of Technology,Harbin 150090,China)

To improve emergency response efficiency under uncertainty,the urban emergency vehicle scheduling model is optimized by the use of mathematical planning.Existing scheduling models are only built in accordance with current incidents while ignoring future incidents.Differently,to prevent future incidents, this paper establishes the mathematical formula which minimized the overall response time cost with weight as the objective function.From the perspective of time and space constraints,travel time calculation of emergency vehicle is discussed under different traffic flow.Case results show that,if the potential incidents really occur,the overall response time cost will be minimized by the scheduling policy.Furthermore, confidence level is selected to measure what extent the future incidents should be considered in response system.Meantime future serious incidents should be focused on prevention as confidence level tends to one, while current incidents would be responded with a priority as confidence level tends to zero.

traffic engineering;emergency;vehicle scheduling;uncertainty;travel time

1009-6744(2014)01-0187-05

U491

A

2013-05-14

2013-08-03录用日期:2013-08-14

国家自然科学基金资助(51308165);哈尔滨工业大学科研创新基金资助(HIT.NSRIF.2014134);山东省科技攻关项目 (2009GG20008020).

赵韩涛(1978-),男,河南开封县人,讲师,博士.*通讯作者:zht1919@163.com