基于时空网络的航班机型分配问题研究

乐美龙,黄文秀

(上海海事大学 科学研究院,上海 201306)

基于时空网络的航班机型分配问题研究

乐美龙*,黄文秀

(上海海事大学 科学研究院,上海 201306)

机队规划是航空公司高效运营的重要前提.本文通过构建基于时空网络的航班机型分配模型,以及乘客溢出量函数和航班机型分配成本函数,为航空公司设计了一种航班机型分配的方法.基本思想是在已知航空公司航班计划、乘客需求分布、机队结构、机型数量的基础上,首先通过构建时空网络图得出航班机型分配模型所需的参数.然后通过求解航班机型分配模型,得到使航班机型分配总成本最小的航班机型配置方案和机队配置方案.最后通过算例验证了上述方法科学、有效,能够为航空公司航班机型分配提供决策支持.

航空运输;机型分配;时空网络;机型;航班

1 引 言

机型分配是指在给定航班计划的条件下,已知机队结构、飞机数量及每种机型飞每条航线的成本,航空公司确定每条航线用什么机型来飞,使其总利润最大或总成本最小.近年来,随着航空运输业的迅速发展,航空公司的市场竞争逐步加剧,国内各航空公司正在采取多种措施来提高其管理水平,包括优化航线网络、优化资源分配等方式.目前有关航空公司机型分配的研究主要集中在如下方面.

国外的 Brown[1]通过构建基于面板数据的模型分析了航空管制因素对其机队构成的影响,文章主要侧重于对枢纽轮辐式航空公司机队规划的研究,但其考虑的影响因素较少.Hane 等人[2]构建了一种基于时间拓展网络的多商品流模型,用于解决机队分配的大规模整数规划问题,在模型求解中用到了内点算法,并通过数据验证了该模型和算法在解决大规模整数规划问题上的优越性.Bahram 等人[3]在 Brown 模型的基础上,构建了基于市场结构和生产技术因素的机队规划模型,通过数据验证了航空公司机队构成受这两个因素影响.Barnhart等人[4]提出了一种 IFAM(Itinerary-Based Fleet Assignment Model) 模型, 首先介绍了基本的FAM(Fleet Assignment Model)模型和PMM模型(Passenger Mix Model), 在 PMM 模型的求解中用到了列生成算法,然后,在 FAM 和 PMM 模型的基础上,构建了 IFAM 模型,模型求解用到了分枝定界法.Listes 等人[5]提出了一种基于时空网络的机队分配模型,模型考虑到了乘客的动态需求,在模型求解中用到了情境聚合算法,最后通过实际数据验证了模型和算法的可行性和优越性.Ahuja 等人[6]用大规模邻域搜索算法对机型分配模型进行求解,该方法考虑到了连续航段上同一机型的指派,最终不仅生成了机型的分配方案,而且还生成了连续的航班段.Sherali 等人[7]提出了一种两阶段的机队分配模型,模型同样考虑了随机乘客需求,模型求解中用了 Benders 分解算法.Barnhart等人[8]在区别 FAM 和 IFAM 的基础上,提出了一种GFAM(Generic Fleet Assignment Model) 模型,该模型以最大化航空公司利润 为目标函数.Sherali 等人[9]综合了航班计划和机队分配模型,目标函数是最大化航空公司收益,约束包括:航班覆盖约束,飞机流约束,飞机资源约束和乘客需求约束等,求解过程用了 Benders 分解算法和 Polyhedral 分析.

国内段晓江[10]等人综合研究了机队和航班计划联合优化问题,但是,模型中没有考虑到乘客需求随机性的影响.孙宏[11]等人综合考虑了乘客不确定性需求,构建了机型分配与飞机排班一体化的数学模型,实现了机队集中调度.乐美龙[12]等人提出了一种多机型不正常航班恢复的时空网络模型.

本文提出了一种基于时空网络图的航班机型分配模型和方法.基本思想是:在已知航空公司航班计划、乘客需求分布、机队结构、机型数量的基础上,首先通过构建时空网络图得出航班机型分配模型所需的参数,然后通过航班机型分配模型,得到使航班机型分配总成本最小的航班机型配置方案.

2 航班公司机型分配问题

2.1 时空网络概述

时空网络中纵轴代表时间,横轴代表机场.网络由若干个弧和结点构成.网络中的结点包含了机场在该时间结点的所有活动,包括飞机的起飞、降落、过夜等.进入结点的弧表示在该时间段内某架飞机降落该机场,从结点出发的弧表示在该时间段内某架飞机从该机场起飞.网络中的弧表示航班.

2.2 时空网络结构

如图1 所示,该时空网络图包含 4 个机场,3种机型,其中,横轴表示机场,分别是机场 A、机场B、机场 C、 机场 D. 纵轴表示时间, 从 10:00-17:00.连线(箭头) 表示航段,结点表示某个机场在一天中某个特定时间航班的进出港情况.图中,折线(带箭头)表示地面连接线,用于将机场的最后一个结点与第一个(或非第一个)结点连接起来,这种线表示飞机在该机场过夜,它将某一天的最后一个进港航班与第二天的出港航班衔接起来,过夜期间可以对飞机进行检修及保养.

图1 时空网络示例Fig.1 An example of time-space network

2.3 机型分配模型

集合:

F ——航班集合;

J ——机型集合;

C ——终止结点集合,且 C ⊆ M;

M ——时空网络中的所有结点集合;

下标:

i——航班下标,i∈ F;

j——机型下标,j∈ J;

k ——终止节点下标,k ∈ C;

m ——时空网络中所有结点下标,m ∈ M.

参数:

ci,j——用机型 j飞机执飞航班 i的成本;

ck,j——机型 j的机组成员在终止结点 k 所在机场的过夜成本;

Nj——机型 j的可用飞机数量;

Si,m=1——结点 m 的航班 i是进港航班;

Si,m=-1——结点 m 的航班 i是出港航班;

CAPj——机型 j的容量;

Demandi——航班 i的平均需求量;

di——航班 i的航程;——结点 k 所 在机 场在 时间 段内最多降落飞机数量;——结点 k 所在机场在时间段内最多起飞飞机数量;

nk——结点 k 所在机场的最小过夜飞机数量(目的保证航班正常运营);

am,k=1——结点 m 是终止结点,即 m=k;

am,k=0——结点 m 不是终止结点,即 m ≠ k.

决策变量:

xi,j=1——航班 i分配给机型 j,否则,xi,j=0;

Gm,j——机型 j在结点 m 的飞机数量(Gm-,j表示机型 j在结点 m 的前一个结点的飞机数量); Gk,j——机型 j在终止结点 k 的飞机数量.

模型:

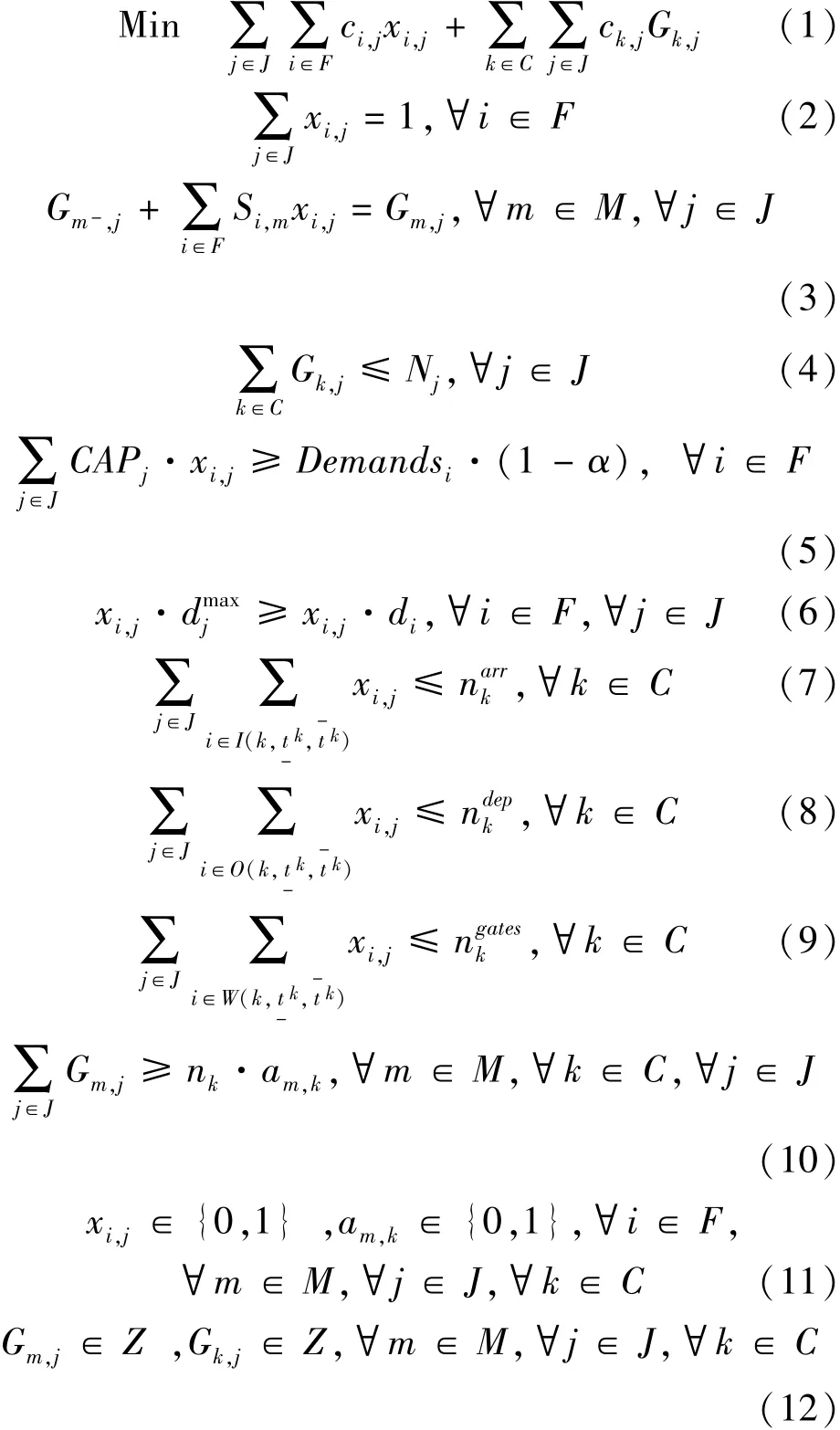
目标函数(1)表示最小化航班机型分配成本;约束(2)为航班覆盖约束,确保任何一个航班都由一个机型来执行;约束(3)为飞机平衡约束条件,确保任何一个结点的飞机流平衡;约束(4)为机型数量约束,保证每种机型过夜结点的数量之和不超过其最大数量;约束(5)为机型容量约束,确保各结点实际登记乘客人数小于等于飞机的最大容量;约束(6)为航程约束,确保各结点飞机的最大航程大于等于以该结点出发的航班的航程;约束(7)为结点单位时间段内飞机到达约束,确保结点 k所在机场在时间 段内飞机到达数量不超过其最大到达能力限制;约束(8)为结点单位时间段内飞机起飞约束,确保结点 k 所在机场在时间段内飞机起飞数量不超过其最大起飞能力限制;约束(9)为单位时间段内结点所在机场的可用飞行跑道数量限制,确保结点 k 在时间段内占用飞机跑道的飞机不超过机场该时间段内的可用飞行跑道数量;约束(10)为终止结点最小过夜飞机数量约束;约束 (11) 表 示 xi,j为 0-1 决 策变量,am,k为 0-1 协变量;约束(12)确保 Gm,j、 Gk,j为整数.

3 算 例

该算例涉及 42 个航班,84 个结点,3 种机型,8个机场,航班计划如表1所示.

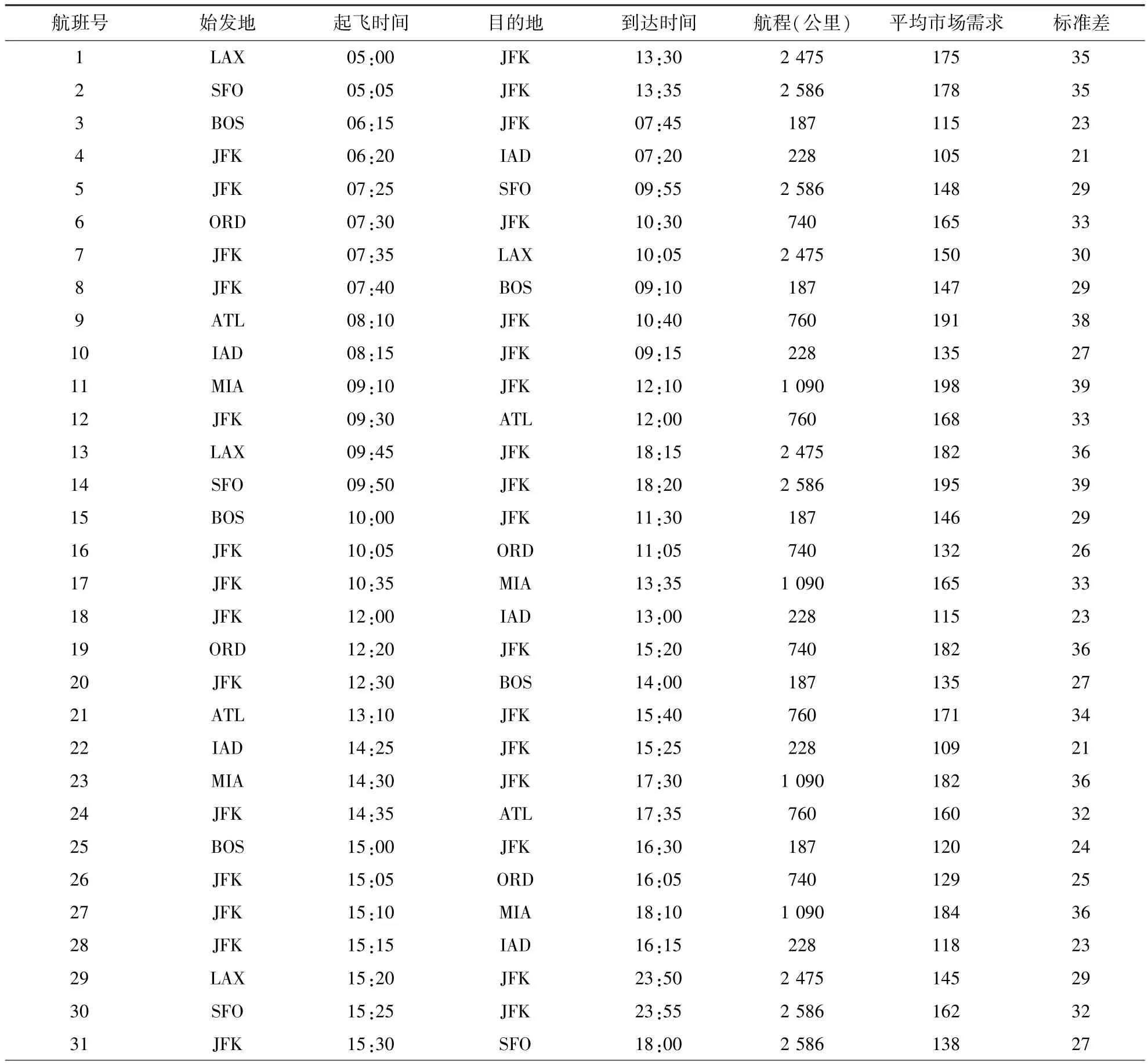
表1 航班计划Table1 The schedule of flights

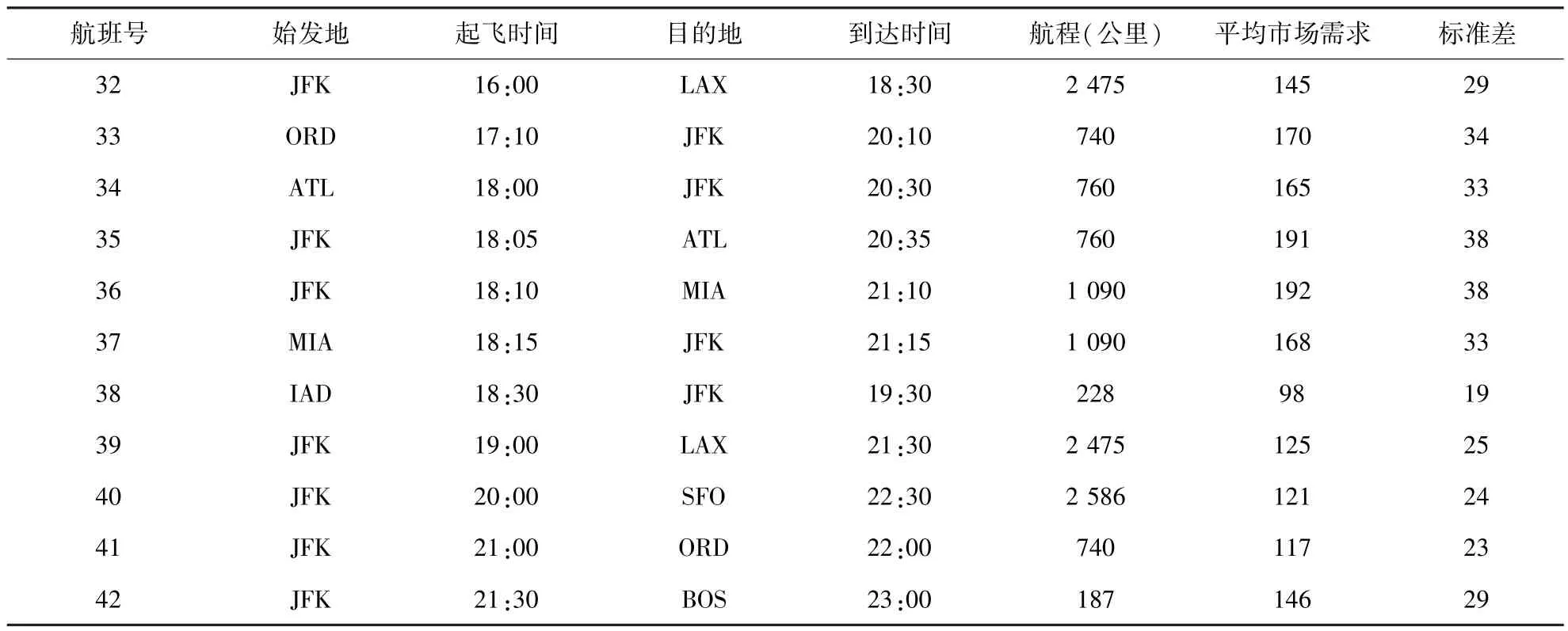
续表

图2 时空网络Fig.2 The time-space network

3.1 构建时空网络图

通过 2.2 节所述的时空网络结构,运用如下方法构建图2的时空网络所示,并通过时空网络数据用 C++语言编程输出 Si,m、am,k.步骤如下:

Step1确定各机场所有航班的起飞和到达时间.

Step2将所有机场进行编号,L=1,2,3,…,8.

Step3将机场 L=1 的所有航班起飞时间和降落时间按照时间顺序进行编号,m=1,2,3,…,k;

If m=k 是从机场 L=1 出发或到达机场 L=1的最后一个航班结点,则定义 k结点为机场 L=1的终止结点,k∈C,

else m 为任意结点,且C⊆ M.

Step4将机场 L=2 的所有航班起飞时间和降落时间按照时间顺序进行编号,m=k+1,k+2,…,k';

If m=k'是从机场 L=2 出发或到达机场 L= 2 的最后一个航班结点,则定义 k'结点为机场 L=2的终止结点,k'∈ C,

else m 为任意结点,且C⊆ M;

for all(L=3,4,5,6,7,8)按照顺序do(Step4).

Step5for all(m ∈ M)do

If m 为航班 i∈ F 的出港航班,则 Si,m=-1, else Si,m=1.

Step6for all(m ∈ M,k ∈ C)do

If m=k 为航班 i∈ F 的出港航班,则 am,k=1,

else am,k=0.

Step7输出 C,M,Si,m,am,k.

3.2 乘客溢出量和航班机型分配成本的计算

三种机型 B737-800、B757-200、B767-200 的CASM(可用座公里成本) 分别为 0.042 美元、0.044 美元、0.043 美元,RASM(可用座公里收入)为 0.15 美元;三种机型的机组成员在非枢纽机场过夜的成本分别为 1200 美元、1400 美元、1 000美元,在枢纽机场过夜的成本分别为 500 美元、600美元、400 美元;可提供的飞机数量分别为 9 架、5架、2 架;机型容量分别为 162、200、214.乘客溢出量和航班机型分配成本的计算方法如下:

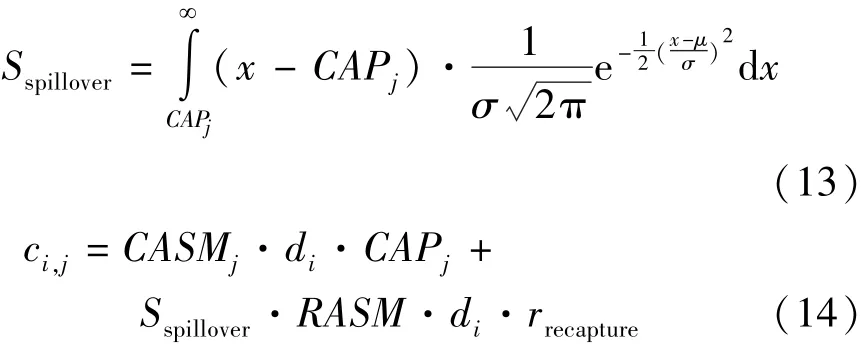
式(13) 为乘客溢出量的计算,Sspillover表示乘客溢出量,CAPj为机型 j∈ J 的容量,乘客的需求服从 (μ,ρ2) 的正态分布[13];式(14) 为航班机型分配成本的计算,包括两部分:运营成本和溢出成本,rrecapture表示航空公司的再捕获率 ( 即从某航班上溢出但是又可以转签到该航空公司其他航班上旅客人数的百分比),设定为 15%,各机场(按照顺序)的最小过夜飞机数量为 2、2、0、5、0、0、0、0.

3.3 分配方案

通过 IBM ILOG CPLEX 12.2 软件对航班机型分配模型进行求解,运行环境为英特尔 酷睿2双核 T6570@2.1GHz 笔记本处理器、5120MB 内存、64 位 Windows 7 操作系统,求解时间为 4.75 s.最小分配成本为 423 864.820 美元,分配方案如表2和表3所示.

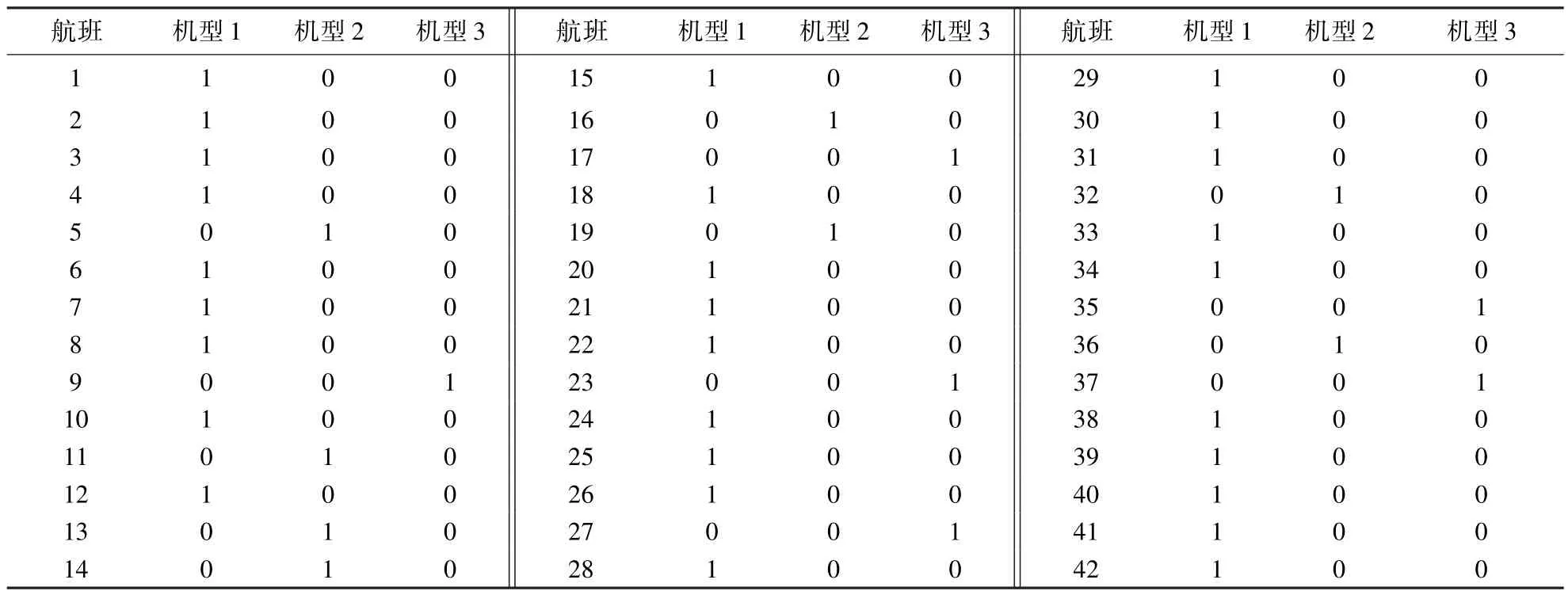
表2 航班机型分配Table2 Airline fleet assignment

表3 机场过夜飞机数量_Table3 The number of overnight aircrafts at various airports

通过计算得出该航空公司的客座率达到85.55%,而通常情况下,航空公司的客座率不超过81.00% 左右.此时,航空公司需求的总的飞机数量是 16 架,为了获得更好的机队配置组合,可以通过调整机队的机型配置,以获得总成本较小和客座率较高的配置方案.表4为部分配置方案的成本和客座率.从表中可以看出,虽然方案 9 的客座率不高,但是其机队配置的总成本最小.此外,该表可以为航空公司的机队规划管理提供决策支持.各方案的航班机型配置表不再一一列出.

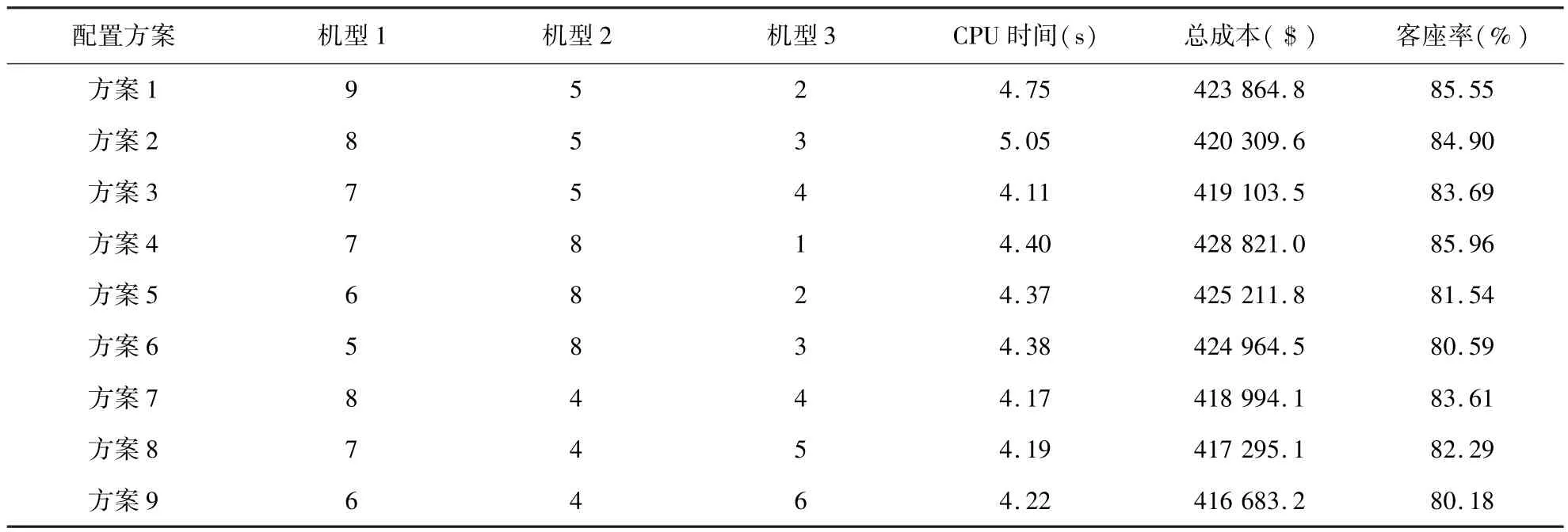
表4 机队配置方案的成本与客座率Table4 The cost and seat kilometer utilization of fleet configuration schemes

4 研究结论

本文通过模拟航空公司运营环境中的航线网络特征、航班计划、乘客需求分布、机队结构、机型数量,提出了一种基于时空网络的航班机型分配模型,并且通过乘客溢出量函数和航班机型分配成本函数准确计算机型分配的成本.此外,目标函数中考虑到了飞机机组人员在外过夜成本,与传统的机型分配模型相比更加准确详细.通过算例发现,本文设计的机型分配方法的平均计算时间相对较短,为 4.40 s,且生成的分配方案的平均客座率相对较高,为 83.15%,能够为航空公司航班机型分配提供决策支持.

[1] Brown J.Airline fleet composition and deregulation [J].Review of Industrial Organization,1992,8 (4):435-449.

[2] Hane C A,Barnhart C,Johnson E L,et al.The fleet assignment problem: Solving a large-scale integerprogram [J]. MathematicalProgramming, 1995,70(2):211-232.

[3] Bahram A,Garland C,Kambiz R.The effects of market structure and technology on airline fleet composition afterderegulation [J]. Review of Industrial Organization,1999,15(1):77-88.

[4] Barnhart C,Kniker T S,Lohatepanont M.Itinerarybased airline fleet assignment[J],Transportation Science,2002,36(2):199-217.

[5] Listes O,Dekker R.A scenario aggregation-based approach for determining a robustairline fleet composition fordynamiccapacityallocation [J]. Transportation Science,2005,39(3):367-382.

[6] Ahuja R K,Goodstein J,Mukherjee A,et al.A very large-scale neighborhood search algorithm forthe combined through-fleet-assignmentmodel[J].Informs Journal on Computing.2007,19(3),416-428.

[7] Sherali H D,Xiaomei Zhu.Two-stage fleet assignment model considering stochastic passengerdemands[J]. Operations Research,2008,56(2):383-399.

[8] Barnhart C,Farahat A,Lohatepanont M.Airline fleet assignment with enhanced revenue modeling[J]. Operations Research,2009,57(1):231-244.

[9] Sherali H D,Bae K H,Haouari M.Integrated airline scheduledesign and fleetassignment: polyhedral analysis and benders'decomposition approach[J]. Informs Journalon Computing. 2010, 22(4): 500-513.

[10] 段晓江,冯允成. 启发式民用飞机机队规划[J]. 北京航 空 航 天 大 学 学 报,1996,22(4):504-508. [DUAN X J,FENG Y C.Efficient heuristic algorithm to airline fleet planning[J]. Journal of Beijing University of Aeronautics and Astronautics,1996,22 (4):504-508.]

[11] 孙宏,张翔,徐杰. 航空公司机队集中调度理论研究[J].中国管理科学,2008,16(1):86-89.[SUN H, ZHANG X,XU J.The theory of integrated airline fleet dispatching[J].Chinese Journal of Management Science,2008,16(1):86-89.]

[12] 乐美龙,王婷婷,吴聪聪.多机型不正常航班恢复的时空网络模型[J].四川大学学报(自然科学版), 2013,50(3):477-483.[LE M L,WANG T T,WU C C.The time-band model for recovery of multi-type aircrafts'disrupted flights[J].Journal of Sichuan University(Nat Sci Ed),2013,50(3):477-483.]

[13] T S Kniker, C Barnhart. Shortcomings ofthe conventional airline fleet assignment model[C].In Proceeding:Tristan Ⅲ,pages 17-23,Puero Rico, June 1988.

Airline Fleet Assignment Model Based on Time-space Network

LE Mei-long,HUANG Wen-xiu
(Academy of Science,Shanghai Maritime University,Shanghai 201306,China)

The fleet planning is an important prerequisite for the airlines'efficient operations.A method is provided for the airline fleet assignment model,which is based on a time-space network,a function of passengers'spillover,and a cost function of airline fleet assignment.Based on the known conditions of airline's flight planning,passengers'demand distribution,fleet structure and the number of aircraft types, the parameters of airline fleet assignment model are obtained from the time-space network.The new schemes of minimizing the cost of airline fleet assignment and fleet configuration are got by solving the airline fleet assignment model.The instance verifies the method to be scientific and effective.It provides the foundations for decision making of airline fleet assignment.

air transportation;airline fleet assignment;time-space network;aircraft types;flights

1009-6744(2014)01-0081-07

N945.15

A

2013-07-15

2013-09-30录用日期:2013-10-23

上海市自然科学基金创新行动计划项目(10190502500);上海市科委工程中心项目(09DZ2250400);上海市教委重点学科项目(J50604).

乐美龙(1964-),男,浙江宁波人,教授,博士生导师.*通讯作者:meilongle@hotmail.com