基于自适应 Agent的地铁站台乘客集散仿真研究

许 奇, 毛保华*,b, 李明高, 冯旭杰

(北京交通大学 a. 城市复杂系统理论与技术教育部重点实验室;b. 中国综合交通研究中心,北京 100044)

基于自适应 Agent的地铁站台乘客集散仿真研究

许 奇a, 毛保华*a,b, 李明高a, 冯旭杰a

(北京交通大学 a. 城市复杂系统理论与技术教育部重点实验室;b. 中国综合交通研究中心,北京 100044)

作为提高地铁运行效率与服务水平的基础研究,地铁乘客集散仿真应综合考虑建筑环境、设施配置、运输组织三方面对乘客集散效率的影响.本文构建了乘客自适应Agent模型,从环境感知、行为决策、动作执行三方面建立基于神经元模型的环境拥挤感知模型,考虑拥挤的运动行为启发规则、运动状态离散更新规则.在构建乘客微观行为动力学模型的基础上,以典型的地铁岛式站台乘客集散为研究对象,建立地铁站台乘客集散仿真模型.仿真结果表明,在地铁站台建筑空间环境和设施设备配置确定的情况下,乘降客流需求和列车发车间隔对地铁站台最大乘客数及乘客集散效率影响显著.

城市交通; 地铁; 微观行为模型; 自适应 Agent; 乘客集散仿真; 拥挤感知建模

1 引 言

站台作为地铁系统与乘客直接交互的服务平台,其拥挤状态下的乘客集散行为呈现显著的复杂非线性动态特征,造成乘客移动效率降低,直接影响系统的运行效率与服务质量.因此,研究站台客流集散现象,对运营组织及安全保障具有重要的现实意义.

地铁网络效应的发挥依赖于运营组织与建筑环境的协调配合.由于基础设施投资昂贵、建设周期长,建成后难以对不合理的布局进行改进,因此,国内外学者更多地关注车站建筑环境与乘客交互的协调设计,包括不同区域的服务水平评价[1,2]、设施设备配置布局对乘客集散的影响[3,4]、设施设备疏散能力及瓶颈分析[5,6]、不同区域的乘客流自组 织 现 象[7,8]、 运 输 组 织 方 案 对 乘 客 集 散 的 影响[9].然而,当地铁线网发展到较大规模时,仅依靠增加设施设备规模和提高其能力,已不能满足由网络效应所诱发的复杂客流需求,拥挤成为常态.因此,需综合考虑建筑空间环境、设施设备配置与布局、运输组织对乘客运动行为的影响,分析站台乘客集散时空规律,研究提高乘客在节点移动效率的关键问题.

针对上述问题,本文构建基于自适应 Agent的地铁站台乘客移动仿真及分布计算模型,研究简单规则涌现复杂现象的内在机理,分析典型站台环境下乘客局部行为交互导致的宏观客流时空演化规律.

2 地铁站台乘客拥挤感知模型

2.1 乘客自适应 Agent模型

Agent是具有自主性、学习性和适应性的人工智能程序.自适应 Agent能感知周围环境的改变,并利用认知结果不断修正其内部状态以适应环境的变化.在地铁站台乘客集散仿真模型中,乘客自适应 Agent定义为四元组:

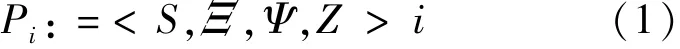
式中 i—— 乘客数,i=1,2, …,N;

S —— 运动状态集合;

Ξ—— 环境感知模型,表示乘客对其周围环境拥挤程度的感知,以获得影响行为决策的主要信息表征;

Ψ ——行为决策模型,表示乘客 Agent根据感知信息和决策规则完成知识推理,并做出合理的运动行为决策;

Z —— 动作执行模型,表示乘客 Agent运动状态的改变,是行为决策的实现结果.

乘客运动状态集合S为表征乘客运动特征的变量及其状态值组成的集合,定义为:

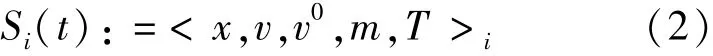
式中 t——仿真时间;

x——位置矢量;

v——速度矢量;

v0——期望速度;

m——乘客质量,由公式 m/160[10]计算乘客在水平面的投影半径;

T——目标点.

2.2 乘客拥挤感知模型

在拥挤感知建模中,乘客通过感知系统获取周围环境信息,经过加工后完成信息筛选和表征,以获得影响决策的关键信息.既有研究[11]表明行人运动过程所获取的感知信息主要来自于视觉.为表征乘客视觉信息,引入离散化的乘客视野范围,如图1 所示.乘客视域由视距 H和视角2φ界定;α0为乘客运动方向与目标点T之间的夹角.

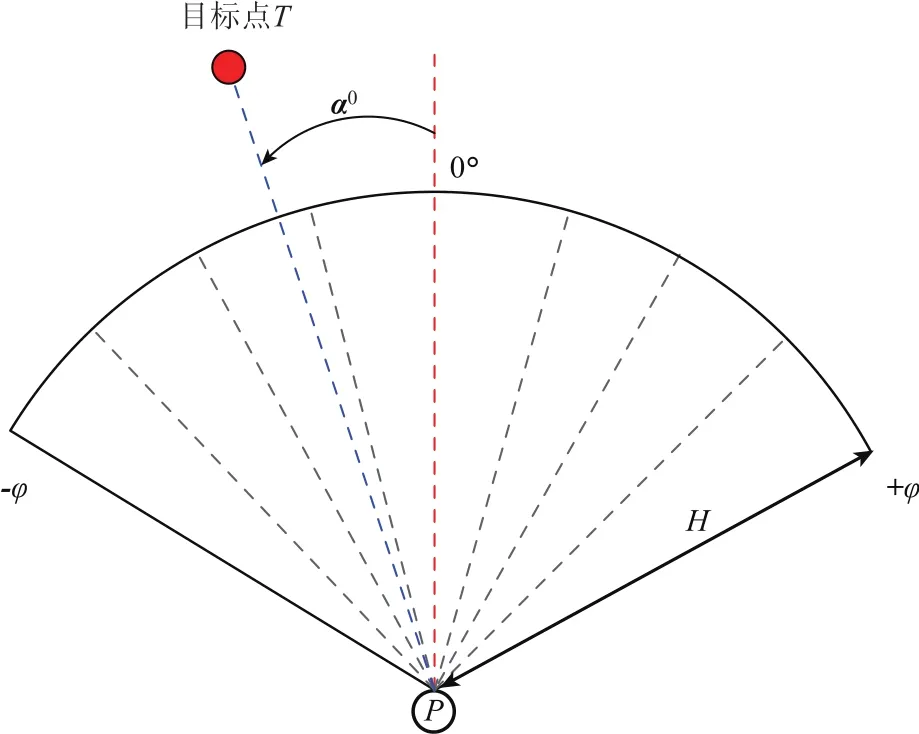
图1 地铁乘客 Agent离散视域Fig.1 The basic geometrical elements of passenger visual field

乘客的运动行为受视觉信息影响显著.既有研究表明[12]处于运动状态的行人通过估计与周围其他行人和障碍物发生碰撞的时间,避免碰撞的发生.同时,乘客的感知能力和认知过程受周围环境的影响,表现为乘客视觉信息的表征依赖于乘客对环境拥挤的感知.因此,基于 Moussaïd 提出的视觉信息表征方法[13],本文建立考虑拥挤的乘客视觉信息表征算法,如式(3)所示.

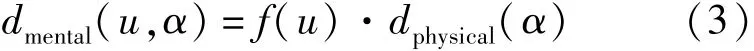
式中 dmental(u, α) —— 视域范围内任意 α 方向,乘客所感知的与其最先发生碰撞乘客或障碍物的心理距离;

dphysical( α) —— 视域范围内任意 α 方向,乘客与最先发生碰撞乘客或障碍物的距离,描述实际发生碰撞的物理距离;

f(u) —— 拥挤感知函数,模拟乘客对周围环境拥挤程度的感知.基于神经元模型,拥挤感知函数 f(u)[10]定义如式(4)-式(7) 所示.

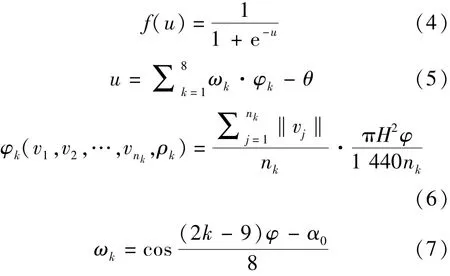
式中 ωk—— 第 k 个子视域的权重;

φk——第k个子视域的视觉信息输入集合;

θ—— 拥挤感知阈值;

v1,v2,…,vk—— 第 k 个子视域范围内 nk个乘客的速度矢量集合;

ρk—— 第 k 个子视域范围内的乘客密度.

3 地铁站台乘客动力学建模

在运动过程中,乘客需在瞬间对当前的环境做出合理的行为决策,任何的逻辑思考和寻优策略均是无效的.基于由有限理性发展而来的生态理性概念,认知启发式描述复杂环境下,人类确保行为合理的决策规则,是快速、简捷的认知过程[14].本文在考虑拥挤效应对乘客运动行为影响的基础上,构建基于认知启发式的乘客运动行为规则,并提出乘客运动状态的离散更新规则.

3.1 运动行为模型

地铁乘客运动行为建模的基础是行人动力学模型;其关键[15]是如何描述乘客运动方向和速度的选择机理.

(1)方向选择规则.

运动过程中的方向选择是行人最重要的行为模式之一.乘客在拥挤环境下的方向选择规则定义为考虑周围其他乘客和障碍物的影响,乘客选择在当前位置 x使其能最快到达目标点 T 的方向,如图2 所示.基于采纳最优启发式规则[14],乘客方向选择规则如式(8)定义.

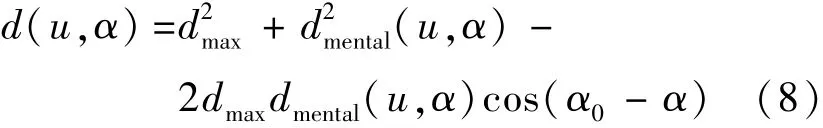
式中 d(u, α) —— 乘客选择移动方向 α 上的第一个乘客或障碍物到视域边界的距离;

dmax—— dphysical的最大值,在数值上等于视距H.

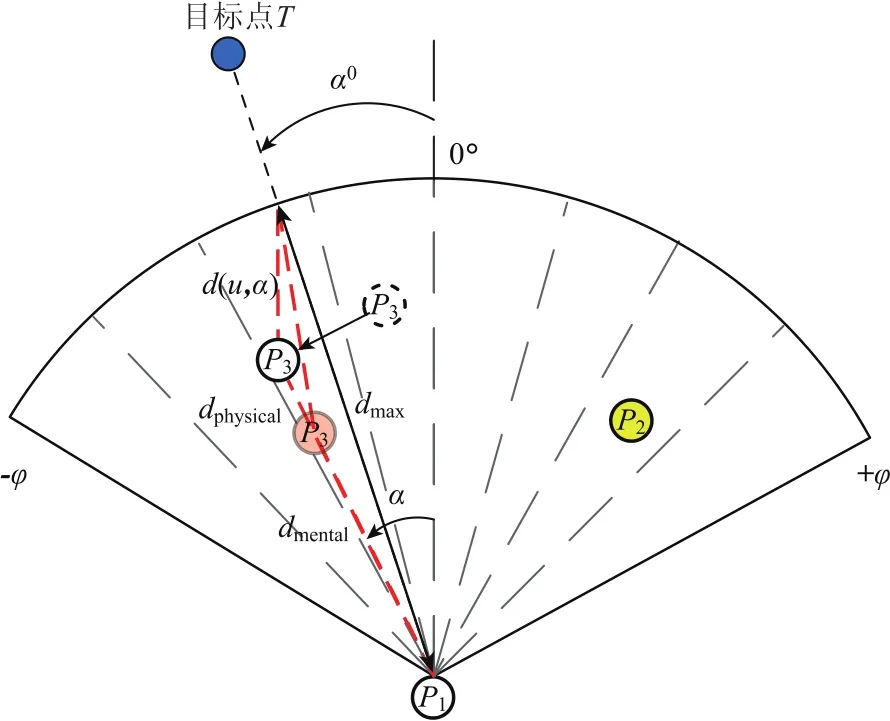
图2 乘客方向选择计算示意图Fig.2 Schematic diagram of passenger walking direction choice decision

(2)速度选择规则.

运动过程中的速度选择是另一种行人最重要的行为模式.乘客在拥挤环境下的速度选择规则定义为在避免碰撞发生的基础上,乘客 t时刻的速度选择 vdes(t) 与周围其它乘客的平均速度 vavg趋同.基于模仿群体行为启发式规则[14],乘客速度选择规则如式(9)定义.

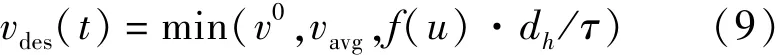
式中 dh—— t时刻,乘客选择移动方向 α 上与第一个乘客或障碍物的距离;

τ ——弛豫时间,表征乘客为适应环境,由行为决策导致运动状态改变的持续时间.

3.2 状态更新规则

在行人动力学建模中,其运动状态可采用连续和离散两种更新机制.地铁站台乘客集散仿真涉及Agent数量较多,针对计算效率与建模细致度的平衡问题,本文采用离散时间更新规则,乘客动力学模型[10]如式(10)和式(11)所示.

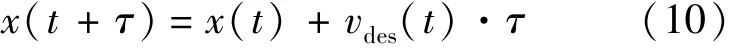
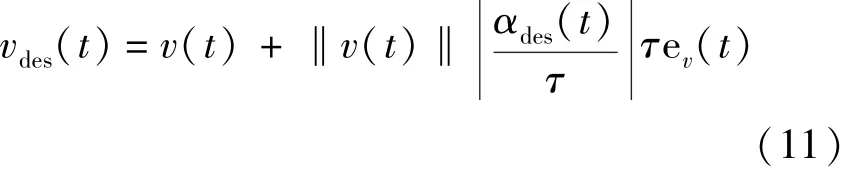
式中 αdes(t)——t时刻乘客选择移动的方向.

4 仿真案例研究

4.1 模型参数及仿真场景

随着网络化运营导致的客流需求不断增加,地铁站台客流分布在时间和空间上均呈现显著的不均衡性.为验证所建立的地铁站台乘客微观行为模型,在乘客拥挤感知和动力学建模的基础上,以典型的地铁岛式站台乘客集散为研究对象,构建基于自适应 Agent的地铁站台乘客集散仿真模型.地铁岛式站台乘客集散仿真模型相关参数如表1所示.

在站台乘客集散仿真场景中,客流需求为乘降乘客数,其中,上车乘客数服从参数为 1.3 的泊松分布,下车乘客数分别为 150 人、200 人、250 人、300 人;上下行列车停站时间均为 30 s,发车间隔分别为 90 s 和 180 s,且上下行列车到站间隔比为1 ∶1.综上,根据乘降客流和列车发车间隔的不同,仿真场景共计 2×4=8 个.地铁岛式站台乘客集散仿真场景如图3所示.

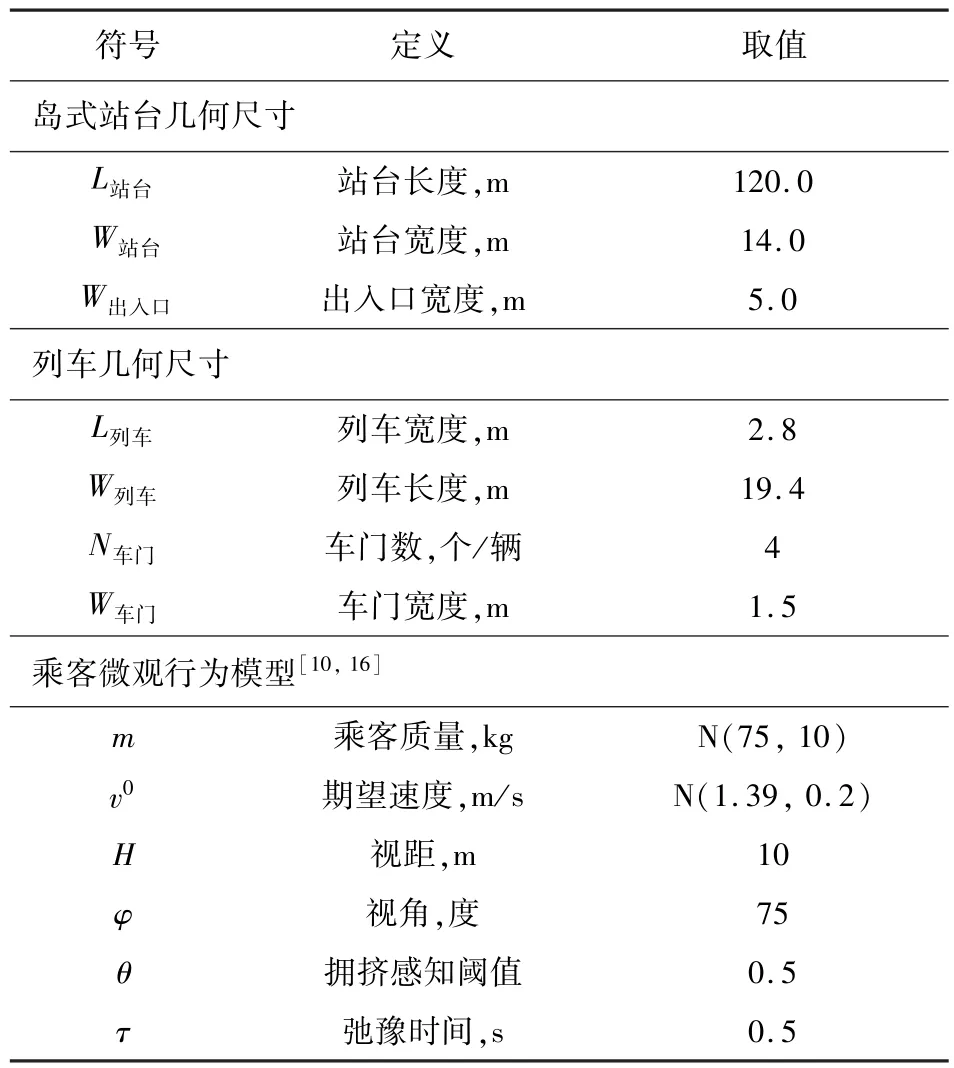
表1 地铁岛式站台乘客集散仿真模型参数Table1 Parameters of the proposed simulation model

图3 地铁岛式站台仿真场景快照Fig.3 Snapshot of simulation for subway island platform

4.2 仿真结果分析

在地铁站台建筑空间环境和设施设备配置确定的情况下,乘客集散时空分布与乘降乘客数量和列车发车间隔相关.通过构建典型地铁岛式站台乘客集散仿真模型,研究不同客流需求,以及列车发车间隔对站台客流时空演化的影响.当列车发车间隔为 90 s,下车乘客数由 150 人变化至 300 人时,站台乘客总数变化趋势如图4所示;其他条件不变,列车发车间隔增加为 180 s 时,站台乘客总数变化趋势如图5所示.

从图4中可以看出,当下车乘客数为 150 人和200 人时,列车到达后导致的站台最大乘客总数基本保持一致,仿真数据表明当乘降乘客需求较小时,出站乘客能及时疏散,站台滞留乘客较少.当下车乘客数为 250 人和 300 人时,列车到达后导致的站台最大乘客总数呈现逐渐增加趋势,其仿真数据表明当乘降乘客需求增大时,出站乘客疏散效率降低,在上下行列车到站间隔内(60 s)不能及时清空站台,导致站台滞留乘客增加.仿真结果表明,当列车发车间隔较小时,随着站台下车乘客数的增加,乘客疏散效率降低,导致不能及时清空站台,站台最大乘客总数呈现逐渐增加趋势.

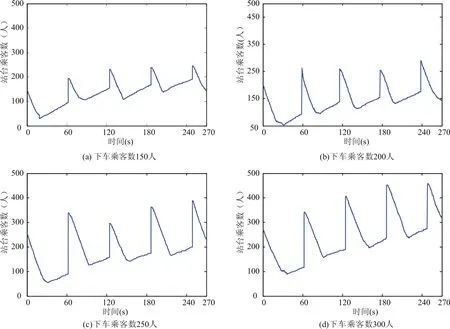
图4 列车发车间隔为 90 s,下车乘客数增加时的站台最大乘客数变化图Fig.4 The time evolution of the number of assembling passengers on platform under train departure frequency is 90 s

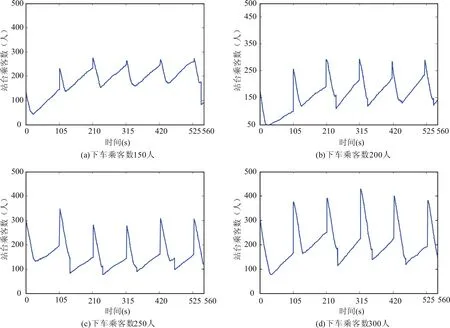
图5 列车发车间隔为 180 s,下车乘客数增加时的站台最大乘客数变化图Fig.5 The time evolution of the number of assembling passengers on platform under train departure frequency is 180 s

从图5中可以看出,当下车乘客数从 150 人增加到 300 人时,列车到达后导致的站台最大乘客总数均保持基本一致.仿真结果表明,列车发车间隔较大时,出站乘客均能在上下行列车到站间隔内(105 s) 清空站台,乘客疏散效率没有随着乘降客流需求的增加而大幅降低,站台滞留乘客较少.

综上,乘降客流需求和列车发车间隔对地铁站台最大乘客数及乘客集散效率影响显著.上下行列车发车间隔的不同步导致列车到站间隔的差异.当上下行列车到站间隔较小时,随着乘降客流需求的增加,乘客集散效率降低,站台最大乘客数呈现逐渐增加趋势;当上下行列车到站间隔较大时,随着乘降客流需求的增加,乘客集散效率降低不显著,站台最大乘客数基本保持一致.

5 研究结论

地铁乘客个体间的局部简单规则可表现站台乘客群体的复杂集散行为.本文通过构建基于神经元模型的环境拥挤感知模型,研究地铁乘客个体运动状态下对环境拥挤的视觉信息表征;在考虑拥挤对乘客运动行为影响的基础上,建立基于认知启发式的乘客运动行为规则,并提出了乘客运动状态的离散更新规则;在构建考虑拥挤的乘客微观行为动力学模型的基础上,以典型的地铁岛式站台乘客集散为研究对象,建立了地铁站台乘客集散仿真模型,研究乘降乘客数量和列车发车间隔的变化对乘客集散效率的影响.仿真结果表明,在地铁站台建筑空间环境和设施设备配置确定的情况下,乘降客流需求和列车发车间隔对地铁站台最大乘客数及乘客集散效率影响显著.

地铁站台乘客集散建模的影响因素复杂繁多.本文构建的模型重点考虑了拥挤效应对乘客运动行为的影响,建立了考虑拥挤的地铁乘客微观行为动力学模型,但模型需要标定的部分参数较为困难,如拥挤感知阈值;其次,模型涌现的仿真结果在一定程度上反映了乘客集散现象,但模型有效性仍需实际数据进行验证.因此,通过设计合理的实验方案,结合视频采集和数据处理技术,采集地铁真实场景的数据,数据标定及验证模型,是作者下一步研究的工作.

[1] Hoogendoorn S P,Bovy P H L.Pedestrian routechoice and activity scheduling theory and models[J]. Transportation Research Part B,2004,38:169-190.

[2] Ma J,Liu S B,Wang W L,et al.Coupling space syntax with network equilibrium model to simulate complex pedestrian flow in transit stations[C]. Transportation Research Board 92nd Annual Meeting,2013.

[3] Daamen W,Bovy P H L,Hoogendoorn S P.Influence of changes in level on passenger route choice in railway stations [J]. Transportation Research Record,2005,1930(1):12-20.

[4] 胡清梅,方卫宁,李广燕,等.地铁车站出口布局对人群疏散性能的影响[J]. 铁道学报,2009,31 (3):111-115.[HU Q M,FANG W N,Li G Y,et al.Influence of exit layout of a metro station on pedestrian evacuation[J]. Journal of the China Railway Society,2009,31(3):111-115.]

[5] 陈绍宽,李思悦,李雪,等.地铁车站内乘客疏散时间计算方法研究[J]. 交通运输系统工程与信息,2008,8(4):101-107.[CHEN S K,LI S Y,LI X,et al.Modeling evacuation time for passengers from metro platforms[J].Journal of Transportation Systems Engineering and Information Technology, 2008,8(4):101-107.]

[6] 陈绍宽, 刘爽, 肖雄, 等. 基于 M/G/c/c 模型的地铁车站楼梯通道疏散能力瓶颈分析[J]. 铁道学报,2012,34(1):7-12.[CHEN S K,LIU S, XIAO X,et al.M/G/c/c-based model of passenger evacuation capacity of stairs and corridors in metro stations[J].Journal of the China Railway Society, 2012,34(1):7-12.]

[7] Zhang Q,Han B M,Li D W.Modeling and simulation of passenger alighting and boarding movement in Beijing metro stations[J].Transportation Research Part C,2008,16(5):635-649.

[8] 张蕊, 杨静, 韩冬, 等. 基于 NOMAD 模型的交通枢纽行人仿真研究[J]. 交通运输系统工程与信息,2011,11(2):52-57.[ZHANG R,YANG J, HAN D,et al.Pedestrian simulation in transportation hub basedonNOMAD model[J].Journalof Transportation Systems Engineering and Information Technology,2011,11(2):52-57.][9] Fiegel J,Banos A,Bertelle C.Modeling and simulation of pedestrian behaviors in transport areas:The specific case of platform/train exchanges[C].International Conference on Computational Science and Applications 2009 Proceedings,2009:129-133.

[10] Xu Q,Mao B H,Feng X J,et al.Effects of crowding perception on self-organized pedestrian flows using adaptive agent-based model[J].arXiv preprint arXiv: 1308.5380,2013.

[11] Batty M.Predicting where we walk[J].Nature,1997, 388(6637):19-20.

[12] Schrater P R,Knill D C,Simoncelli E P.Mechanisms of visual motion detection[J].Nature neuroscience, 2000,3(1):64-68.

[13] Moussaïd M,Helbing D,Theraulaz G.How simple学,2006,12(2):16-18.[PAN X D,DU ZH G, JIANG H,et al.Experiment research on relationship between the variation of drivers'heart rate and systolic blood pressure and alignment of mountainous highway [J].Harbin Institute of Technology,2006,12(2): 16-18.]

[7] Peter Richter,Thomas Wagner,Ralf Hager,et al. Psycho physiological analysis of mental load during driving on rural roads-a quasi-experimental field study [J].Ergonomics,1998,41(5):593-609.

[8] Furuichi,Tomoki,Iwasaki,et al.Drivers'behavior in S curve negotiations on an urban motorway[J].Traffic and Transport.Studies Proc.of ICTTS 2002,2: 849-856.

[9] Bong-Jo Chung.Limit length evaluation of tangent on freeway according to driver's physiological response [J].TRB,2001,ID Number:01-3166.

[10] Ashley Craig,Yvonne Tran.A controlled investigation into the psychological determinants of fatigue[J]. Biological Psychology,2006(72):78-87.

[11] Sibsambhu Kari,Mayank Bhagat,Aurobinda Routray. EEG signal analysis for the assessment and quantification of driver's fatigue[J].Transportation Research Part F,2010,13:297-306. rules determine pedestrian behaviour and crowd disasters[J].Proceedings of the National Academy of Sciences,PNAS,2011,108(17):6884-6888.

[14] Gigerenzer G.Why heuristics work[J].Perspectives on Psychological Science,2008,3(1):20-29.

[15] Antonini G,Bierlaire M,Weber M.Discrete choice models of pedestrian walking behavior[J].Transportation Research Part B,2006,40(8):667-687.

[16] 许奇, 毛保华, 钱堃, 等. 基于认知启发式规则的行人动力学建模[J]. 交通运输系统工程与信息, 2012,12(4):149-154.[XU Q,MAO B H,QIAN K,et al.Cognitive heuristics for modeling pedestrian walking behavior[J].Journal of Transportation Systems Engineering and Information Technology,2012,12 (4):149-154.]

Simulation of Passenger Flows on Urban Rail Transit Platform Based on Adaptive Agents

XU Qia,MAO Bao-huaa,b,LI Ming-gaoa,FENG Xu-jiea
(a.MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology; b.Integrated Transportation Research Center of China,Beijing Jiaotong University,Beijing 100044,China)

Modeling and simulation of passenger flows on urban rail transit platform is a key issue in improving operation efficiency and service of level of urban rail transit,which should consider architectural environment,facilities implementation,and transportation organization.To simulate this kind of passenger for planning or evaluation,3-layer architecture adaptive agent model is proposed to simulate passenger microscopic behaviors,which is based on visual perception module,making-decisions module,and action execution module.In respect of perception of agents,we construct a neuron-model-based perception model of environmental crowding to examine how individual URT passengers on the move represent the visual information of environmental crowding.Then,we define rules for behaviors based on cognitive heuristics for making-decisions module,and propose a discrete rule for the updating of passenger movement state for action execution module.Based on modeling passenger behavior dynamics,a microscopic simulation model for complex passenger flows on urban rail transit platform is developed.As a case study,the passenger flows scenarios of an island platform of urban rail transit station are simulated.Simulation results show that boarding and alighting passengers demand and train departure frequency have a remarkable impact on the maximum number of assembling passengers on platform and efficiency of mustering and evacuating under given conditions of building environment and facilities.

urban traffic;urban rail transit;microscopic behavior model;adaptive agents;passenger mustering and evacuating simulation;crowding perception modeling

1009-6744(2014)01-0028-07

U293.1

A

2013-04-25

2013-09-17录用日期:2013-09-26

国家自然科学基金重点项目(71131001); 国家重点基础研究发展计划项目(2012CB725406); 中央高校基本科研业务费专项资金资助(2012YJS053).

许奇(1982-), 男, 云南普洱市人, 博士生.*通讯作者:bhmao@bjtu.edu.cn