位势井在3个非线性源项波动方程中的应用
李宝平, 帅 鲲, 蒲志林
(1.电子科技大学成都学院,四川成都611731; 2.四川师范大学成都学院,四川成都611745;3.四川师范大学数学与软件科学学院,四川成都610066)
1 预备知识
为了解决不具有正定能量的双曲方程整体解的存在性,1968年,D.H.Sattinger[1]首先引进位势井理论,此方法是一种通过势能项控制非线性项使得系统总能量正定的方法.此后,位势井方法被用来进行各类非线性发展方程解的适定性分析[2-11],大多结果中用位势井方法研究只含有一个半线性项f(u)的方程,如文献[5]中对于给定常数γ>2,假设f(u)满足

再由假设|uf(u)|≤λ|F(u)|可得到|uf(u)|=O(|u|γ).文献[12]研究了f(u)初边值问题解的爆破,其中,f(u)满足单调增加且u>0凸,u<0凹,或f(u)在-∞ 对井深的定义,文献[13]研究了初边值问题,定义了 可以看出,通过Nehari流定义的位势井深度较抽象,研究其性质难度较大,并且也不易将其计算和应用于工程;另外,对于具有复杂源项的波动方程,也希望可以通过位势井深度得知这些非线性项对系统性态的影响情况,因此定义 定理3.1设p,q,r满足条件(H), 则有: (i)若u0(x)∈W,则u(t)∈W,0 (ii)若u0(x)∈V,则u(t)∈V,0 证明(i)由于u0(x)∈W,若u(t)∉W,则必然存在第一个使u(t)∈∂W的时刻t0,0 由引理2.2(ii)可知 这与E(0)=E(t) (ii)由于u0(x)∈V,若u(t)∉V,则必然存在第一个使u(t)∈∂V的时刻t0,0 定义4.1u(x,t)被称为问题(1)~(3)在Ω×[0,T)上的弱解,若 通过借助具单个非线性源项的波动方程,本文引入了新的位势井理论,进一步阐明了具3个非线性源项的波动方程初边值问题解的整体存在性以及有限时间爆破. 在理论和工程应用上本文的工作都是很有价值的,通过重新构建的变分问题,本文计算位势井深度并定义新的位势井,清晰揭示了位势井理论的内部原理,证明了解的初始值对整体适定性的影响,即U0∈W与U0∈V所导致的解的整体存在性.这一讨论和分析清晰地说明了位势井理论处理问题的外部原理,避免了过去复杂估计位势井深度,便于直接有效地对问题进行分析. [1]Sattinger D H.On global solution of nonlinear hyperbolie equations[J].Arch Rat Mech Anal,1968,30:148-172. [2]Tsutsumi M.On solutions of semilinear differential equations in a Hilbert space[J].Math Jpn,1972,17:173-193. [3]Lions J L.Quelques Methodes de Resolution des Problemes aux Limites non Lineaires[M].Paris:Dunod,1969. [4]Nakao N,Ono K.Existence of global solutions to the Cauchy problem for the semilinear dissipative wave equations[J].Math Z,1993,214(2):325-342. [5]Payne L E,Sattinger D H.Sadle points and instability of nonlinear hyperbolic equations[J].Israel J Math,1975,22:273-303. [6]Liu Y C,Xu R Z.Wave equations and reaction-diffusion equations with several nonlinear source terms of different sign[J].Discrete Cont Dyn Syst,2007,7(1):171-189. [7]Liu Y C,Zhao J S.On potential wells and applications to semilinear hyperbolic equations and parabolic equations[J].Nonliear Anal,2006,64(12):2665-2687. [8]Song X F.Blowup and mass concentration phenomena for a system of Schrödinger equation withcombined power-type nonlinearities[J].J Math Phys,2010,51:503-509. [9]舒级.一类带调和势的阻尼非线性Schrödinger方程的爆破性质[J].四川师范大学学报:自然科学版,2009,32(2):143-145. [10]Kametaka Y,Watanabe K,Nagai A.The best constant of Sobolev inequality in anndimensional Euclidean space[J].Proc Jpn Acad,2005,81(3):57-60. [11]刘亚成,徐润章.一类非线性色散耗散波动方程整体解的存在性[J].哈尔滨工程大学学报:自然科学版,2007,28(5):586-589. [12]Glassay R T.Blow-up theorems for nonlinear wave equations[J].Math Z,1973,32:183-203. [13]Liu Y C.On potential wells and vacuum isolating of solutions for semilinear wave equations[J].J Diff Eqns,2003,192(1):155-169.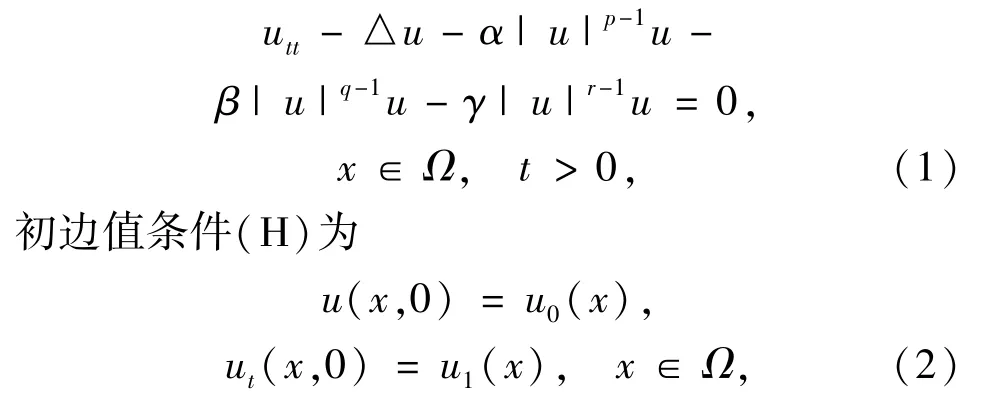
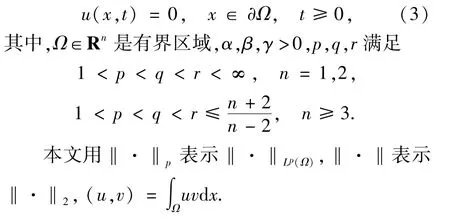
2 位势井深度的计算与位势井的定义




3 解的不变集合
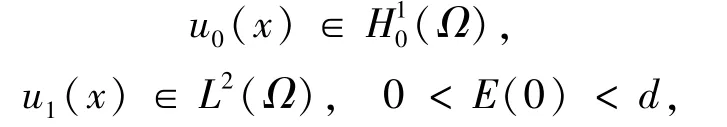


4 解的整体存在性与有限时间爆破




5 结论

