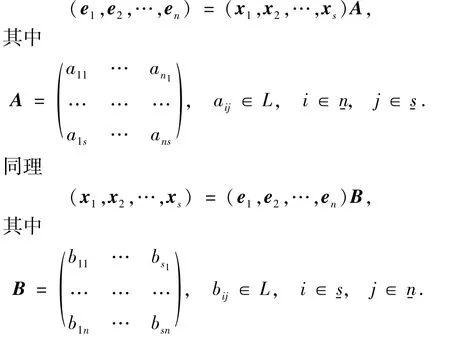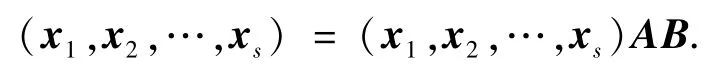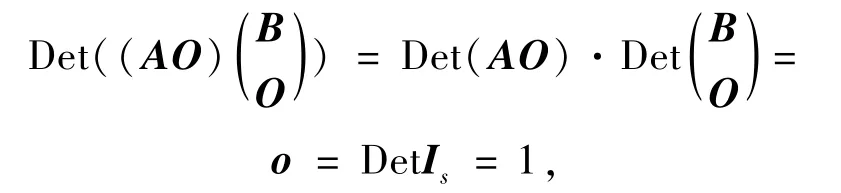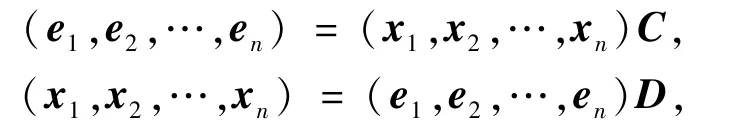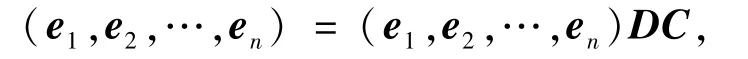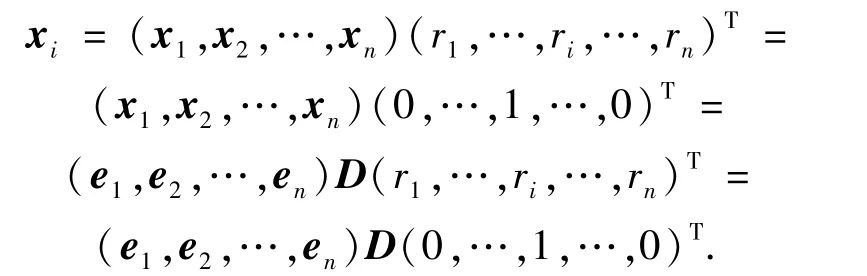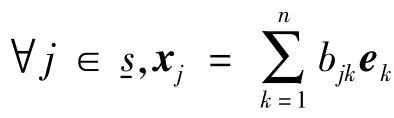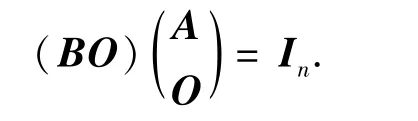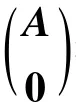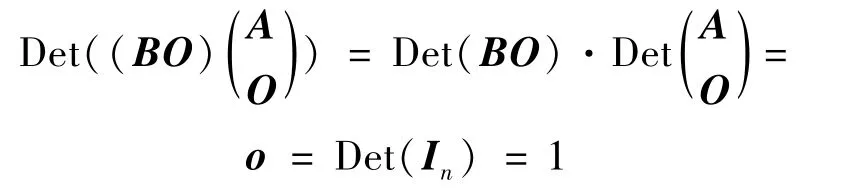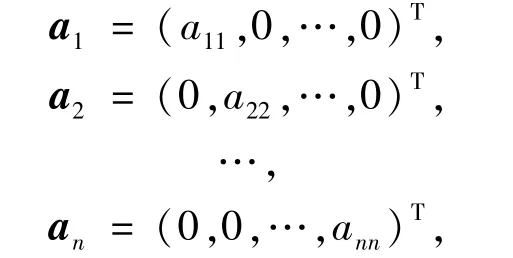半线性空间的基与基数
舒乾宇, 王学平
(四川师范大学数学与软件科学学院,四川成都610066)
研究半环上的半线性结构已经有很长的历史.1979年,R.A.Cuninghame-Green等[1]在 minplus代数中构建了类似于线性代数的一系列理论:线性方程系统、特征值问题、向量组的线性相关性与线性无关性、秩与维数等.1985年,P.Butkoviˇc等[2]引用线性相关与线性无关以及向量组的秩等经典线性代数中的概念来讨论强正则矩阵的相关性质.随后研究者们将这些理论应用到相应的领域,比如选址问题[3]、控制系统问题[4-5]、分离事件系统[6]以及一些代数基本问题[7-14].而随后P.Butkoviˇc[15-16]和K.Cechl rov 等[17]则将线性相关与线性无关、特征值、线性方程的求解等相关的定义和结论类似的引入到max-plus代数中.而在2004年,R.A.Cuninghame-Green等[18]在max-plus代数中证明当空间是有限生成时,该空间有基且每组基的基数相等,最后给出在有限生成的空间中求基的方法.在2007年,A.Di Nola等[19]在MV-代数上建立半线性空间,引入向量组的线性相关、线性无关及基的概念,并解决了相应线性方程组有解的充要条件等问题.同时也提出一些公开问题:在半线性空间中,不同基的基数是否相等的问题,线性无关的向量组能否扩张成基的问题等.2010年,S.Zhao等[20]在join-半环中给出不同基的基数相等的充要条件,而Q.Y.Shu等[21]则在交换的零和自由半环上给出不同基有相同基数的一些充要条件.本文将主要讨论一些零和自由半环上,半线性空间基的一些性质,首先证明半线性空间中不同基有相同基数的充要条件,然后在一类特殊的零和自由半环上证明在其对应的半线性空间中,不同基有相同基数.
1 预备知识
以下假定读者对半环及半环中一些基本概念和符号已经熟悉[22],仅给出文中常用的一些基本概念.
定义1.1设L=〈L,+,·,0,1〉为半环.若对 ∀r,r′∈L,都有r·r′=r′·r,则称 L 为交换半环.若a+b=0蕴含a=b=0,∀a,b∈L,则称半环L是零和自由的.
定义1.2设L=〈L,+,·,0,1〉为半环,a=(A,+A,oA)为一个加法交换幺半群.若外积∗:L×A→A满足对∀r,r′∈L和a,a′∈A都有
(i)(r·r′)∗a=r·(r′∗a);
(ii)r∗(a+Aa′)=r∗a+Ar∗a′;
(iii)(r+r′)∗a=r∗a+Ar′∗a;
(iv)1∗a=a;
(v)o∗a=r∗oA=oA,
则称〈L,+,·,0,1;∗;A,+A,oA〉 为左L- 半模.类似地,还可以定义右L-半模,其中外积的定义为A×L→A.
后面的定义是对文献[1]中定义的半线性空间的一种推广.
定义1.3设L=〈L,+,…,0,1〉是半环,称L上的半模为L-半线性空间.
注意,在定义1.3中,半模即是指左L-半模.方便起见,以下令表示集合{1,2,·s,n},其中n是任意正整数.
例 1设L=〈L,+,·,0,1〉是半环,对n≥1,令

其中(x1,x2,…,xn)T表示(x1,x2,…,xn)的转置.对∀x= (x1,x2,…,xn)T,y= (y1,y2,…,yn)T∈Vn(L)和r∈L,定义运算为
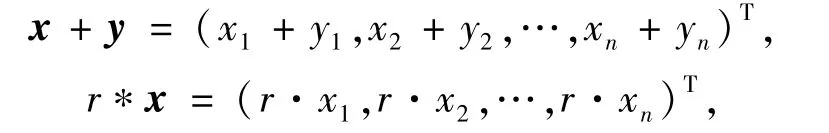
则 Vn= 〈L,+,·,0,1;∗;Vn(L),+,on×1〉 为 L-半线性空间,其中on×1=(0,0,…,0)T.也称 Vn为半环L上的n维向量空间.
为方便起见,下面在不会引起混淆的情况下,在L-半线性空间〈L,+,·,0,1;∗;A,+A,oA〉中,将用ra来代替r∗a,其中∀r∈L,a∈A.
定义 1.4设〈L,+,·,0,1;∗;A,+A,oA〉 是L-半线性空间,称表达式
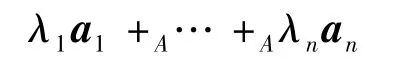
为A中向量组a1,…,an的线性组合,其中λ1,λ2,…,λn∈L为标量(也称系数).若向量x能表示成向量组a1,a2,…,an的线性组合,则称向量x能被向量组a1,a2,…,an线性表出或线性表示.
定义1.5在L-半线性空间中,单个向量a是线性无关的.若向量组a1,a2,…,an(n≥2)中的任一向量都不能被其余向量线性表出,则称该向量组是线性无关的,否则,称向量组a1,a2,…,an是线性相关的.若无限集合的任意有限子集都是线性无关的,则称此无限集合是线性无关的.
注意到,半线性空间或半模中相应的线性相关和线性无关的概念曾被许多学者研究过[2,19,22,24-25].
设S是L-半线性空间的一个非空子集,若L-半线性空间中的任意向量都能表由集合S中的向量线性表出,则称S是L-半线性空间的一个生成集[19].令S表示L-半线性空间a的生成集,则可记作a= 〈S〉.特别地,若S={a1,…,ap},则记作a= 〈a1,…,ap〉.
定义1.6[22]称L-半线性空间a中线性无关的生成集为a的基.
定义1.7[21]在L-半线性空间a中,若每一组基都有相同的基数,则称每组基的基数为a的维数,记作dim(a).
设矩阵A∈Mn(L),令P表示集合{1,2,…,n}上的所有置换.定义矩阵A的行列式,记作Det(A).

由以上定义易知Det(A)=Det(AT).
定义1.8设向量x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T∈Vn,则x和y的内积记作(x,y),等于它们对应分量乘积的和
(x,y)=x1·y1+x2·y2+ … +xn·yn.
定义1.9在半环L=〈L,+,·,0,1〉中,设a∈L,若存在b∈L使得ab=ba=1,则称元素a是可逆的,b为a的逆元,记作a-1.用U(L)表示半环L中所有可逆元构成的集合.
定义1.10矩阵A∈Mn(L)称为左可逆(或右可逆)的,如果存在矩阵B∈Mn(L)使得AB=In(或BA=In).若矩阵A既是左可逆的又是右可逆的,则称它是可逆的.
自现在起,都假设L=〈L,+,·,0,1〉是交换的零和自由半环.
引理 1.1[26]设A,B∈Mn(L),若存在k∈使得对∀j∈都有ajk=0,那么Det(A)=0.
引理1.2[27]设A∈Mn(L),则下列条件等价.
1)A是左可逆的;
2)A是右可逆的;
3)A是可逆的;
4)AAT是可逆的对角阵;
5)ATA是可逆的对角阵.
引理1.3[27]设矩阵A,B∈Mn(L),若A是可逆的,则有 Det(AB)=Det(A)·Det(B)和Det(BA)=Det(B)·Det(A)都成立.
2 L-半线性空间Vn的基的基数
显然向量组e1,e2,…,en是L-半线性空间Vn的一组基,其中
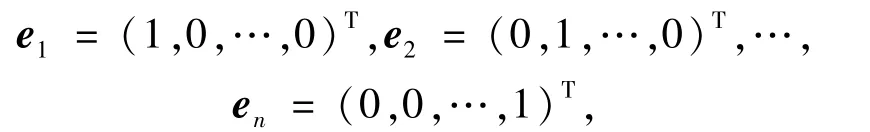
称e1,e2,…,en为Vn的标准基[20].

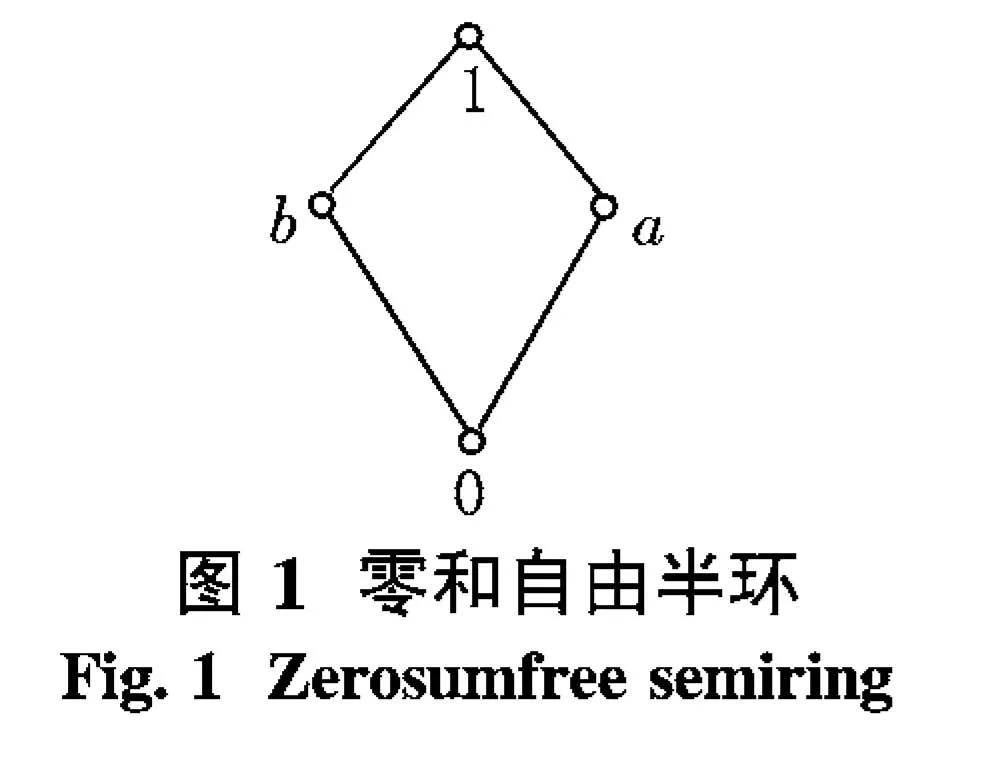
引理2.1在L-半线性空间Vn中,不同的基有相同的基数的充要条件是:任何一个基中的向量都可以由其所在的基唯一线性表出.
证明 充分性设x1,x2,…,xs是Vn的任意一组基,由已知有∀xi,i∈,都可由x1,x2,…,xs唯一的线性表出.只需证n=s.若n≠s,则必有n 因此 又由已知,任何一个基中的向量都可以由其所在的基唯一线性表出,可知AB=Is.由于s>n,则将矩阵A补上s-n列O,而将矩阵B补上s-n行O,使之都变成方阵,则有 一方面,由引理1.2知方阵(AO)和(B)都是可逆矩阵,另一方面,两边取行列式,由引理1.1和1.3知 矛盾.同理,也可由s 必要性若L-半线性空间Vn中,不同基有相同的基数,则不妨设{x1,x2,…,xn}为Vn的任意一组基.对 ∀xi∈ Vn,i∈,设 其中ri∈L,i∈.由充分性的证明,不妨设 其中C,D∈Mn(L),则有 因此DC=In,也就是说,D是可逆矩阵.从而 因此D(r1,…,ri,…,rn)T=D(0,…,1,…,0)T.而D是可逆的,即(r1,…,ri,…,rn)T=(0,…,1,…,0)T,也就是说,任一向量xi都能被其所在基{x1,x2,…,xn}唯一的线性表出. 引理2.2[21]在L-半线性空间Vn中,每组基有相同的基数的充要条件是:任一向量都可以由基唯一的线性表出. 由引理2.2易得推论2.1. 推论2.1[23]在L-半线性空间Vn中,下列条件等价: (1)每组基有相同的基数; (2)任一向量都可以由基唯一的线性表出; (3)任何一个基中的向量都可以由其所在的基唯一线性表出. 显然定理2.1是对引理2.1的改进. 从定理2.1前的例子可以看出,并不是所有的零和自由半环上的半线性空间Vn中不同基都有相同的基数,下面将给出一种特殊的零和自由半环,使得其对应的半线性空间Vn中不同基有相同的基数. 定理2.2若U(L)=L{0},则dim(Vn)=n. 证明只需证Vn中任意一组基都含有n个向量.设x1,x2,…,xs是Vn的任意一组基,若n≠s,则要么n>s,要么n 从而BA=In.由于n>s,将矩阵A补上n-s行O,而将矩阵B补上n-s列O,使之都变成方阵,则有 矛盾.若n 从而由L是零和自由的,有aikajt(xk,xt)=0,其中i,j∈,i≠j,k,t∈.特别地,aikajk(xk,xk)=0,其中i,j∈,i≠j,k∈.另一方面,由向量组x1,x2,…,xs是线性无关的,显然有(xk,xk)≠0,其中k∈又U(L)=L{0},从而aikajk=0,其中i,j∈,i≠j,k∈,这就意味着矩阵A的每一行恰好有一个非零元.因此不妨设 因为半环L是零和自由的,所以由(5)式可知aikkbkt=0,t≠ik,k∈从而由(4)式有bkt=0,t≠ik,k∈,即矩阵B的每一列至多有一个非零元.而由x1,x2,…,xs线性无关可知矩阵B的每一列都有一个非零元.又由n 由定理2.2的证明可得出推论2.2. 推论2.2若U(L)=L{0},则向量集{a1,a2,…,an}是L-半线性空间Vn的一组基当且仅当 其中,对 ∀i∈,都有aii≠ 0. [1]Cuninghame-Green R A,Minimax A.Minimax Algebra(Lecture Notes in Economics and Mathematical Systems)[M].Berlin:Springer-Verlag,1979. [2]Butkoviˇc P,Hevery F.A condition for the strong regularity of matrices in the minimax algebra[J].Discrete Appl Math,1985,15:133-155. [3]Francis R L,McGinnis L F,White J A.Locational analysis[J].European J Oper Res,1983,12:220-252. [4]Carré B A.Graphs and Networks[M].Oxford:Oxford University Press,1979. [5]Karp R M.A characterization of the minimum cycle mean in a digraph[J].Discrete Math,1978,23:309-311. [6]Cuninghame-Green R A,Huisman F.Convergence problems in minimax algebra[J].J Math Anal Appl,1982,88:196-203. [7]Butkoviˇc P,Cuninghame-Green R A.On the regularity of matrices in min-algebra[J].Linear Algebra and Its Applications,1991,145:127-139. [8]Perfilieva I.Fuzzy function as an approximate solution to a system of fuzzy relation equations[J].Fuzzy Sets and Systems,2004,147:363-383. [9]Perfilieva I.Semi-linear spaces[C]//Noguchi H,Ishii H,et al.Proc of Seventh Czech-Japanese Seminar on Data Analysis and Decision Making under Uncertainty.Hyogo:Japan,2004:127-130. [10]Perfilieva I,Novàk V.System of fuzzy relation equations as a continuous model of if-then rules[J].Information Sciences,2007,177:3218-3227. [11]Perfilieva I,Noskov L.System of fuzzy relation equations with inf- → composition:complete set of solutions[J].Fuzzy Sets and Systems,2008,159:2256-2271. [12]Gondran M,Minoux M.Dioid and semirings:links to fuzzy sets and other applications[J].Fuzzy Sets and Systems,2007,158:1273-1294. [13]Gondran M,Minoux M.Graphs,Dioids and Semirings[M].New York:Springer-Verlag,2008. [14]熊清泉,舒乾宇.完备格上区间值t-半模及其R-蕴含算子[J].四川师范大学:自然科学版,2013,36(2):165-171. [15]Butkoviˇc P.Simple image set of(max,+)linear mappings[J].Discrete Appl Math,2000,105:73-86. [16]Butkoviˇc P.Max-algebra:the linear algebra of combinatorics[J].Linear Algebra and Its Applications,2003,367:313-335. [17]Cechl rov K,Cuninghame-Green R A.Soluble approximation of linear systems in max-plus algebra[J].Kybernetika(Prague),2003,39:137-141. [18]Cuninghame-Green R A,Butkoviˇc P.Bases in max-algebra[J].Linear Algebra and Its Applications,2004,389:107-120. [19]Di Nola A,Lettieri A,Perfilieva I,et al.Algebraic analysis of fuzzy systems[J].Fuzzy Sets and Systems,2007,158:1-22. [20]Zhao S,Wang X P.Invertible matrices and semilinear spaces over commutative semirings[J].Information Sciences,2010,180:5115-5124. [21]Shu Q Y,Wang X P.Bases in semilinear spaces over zerosumfree semirings[J].Linear Algebra and Its Applications,2011,435:2681-2692. [22]Golan J S.Semirings and Their Applications[M].Dordrecht:Kluwer Academic Publishers,1999. [23]Zimmermannn U.Linear and Combinatorial Optimization in Ordered Algebraic Structures[M].Amsterdamn:North-Holland Press,1981. [24]Gondran M,Minoux M.Linear algebra in dioïds:a survey of recent results[J].Ann Discrete Math,1984,19:147-164. [25]Cechl rov K,Pl vka J.Linear independence in bottleneck algebras[J].Fuzzy Sets and Systems,1996,77:337-348. [26]Poplin P L,Hartwig R E.Determinantal identities over commutative semirings[J].Linear Algebra and Its Applications,2007,387:99-132. [27]Tan Y J.On invertible matrices over antirings[J].Linear Algebra and Its Applications,2007,432:428-444.