光电效应测定普朗克常数的Matlab处理设计

王蕴杰，孙燕

光电效应测定普朗克常数的Matlab处理设计

王蕴杰，孙燕

介绍了应用曲率处理光电效应测定普朗克常量实验数据的方法，利用Matlab进行了相应处理程序设计，并应用该方法对实验数据进行了分析、处理，同时，对处理过程中的注意点予以了阐述。结果显示，曲率法应用于光电效应确定普朗克常量的数据时，有较高的精确度，解决了光电效应确定普朗克常量实验截止电压不易确定和实验处理结果误差较大等问题。

普朗克常数；截止电压；Matlab；曲率法

0 引言

普朗克常数是自然界中一个普遍适用常数，利用光电效应测定普朗克常量，主要是通过测量光电管的截止电压与对应光频率ν关系，再经处理后得出h值。其原理如图1所示：

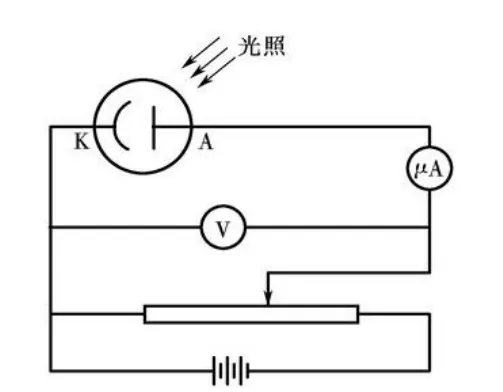
图1 光电效应实验装置

公式（1）中：E为光电子逸出金属表面后的动能，h为普朗克常量，ν为入射阴极K光线的频率，为阴极K金属材料的逸出功。

此时，光电子会落在阳极A上形成光电流，如果阳极A与阴极K之间施加一适当的负电位时，光电子便全部不能到达阳极A，光电流为零，即光电效应的截止电压。此时必然存在有关系，如公式（2）：

公式（2）中e为电子电量。由公式（1）、（2）式可得公式（3）：

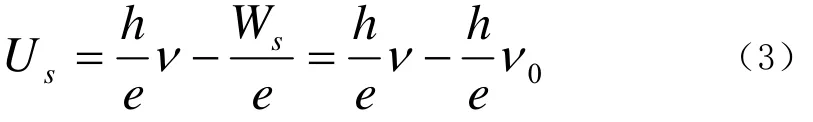
1 光电效应实验数据及曲率法

1.1 曲率法

由原理可知利用光电效应测定普朗克常量的关键在于确定截止电压，由于截止电压两侧的光电管伏安特性曲线呈现不同函数关系，故将截止电压对应点称为“拐点”，“拐点”确定的准确度是影响实验精度的关键。

曲率法处理实验数据过程是测量不同频率光照下的不同电压对应的光电流大小，然后根据测得数据绘制出光电管伏安特性曲线，然后将测量得到的伏安特性曲线用同一函数拟合，对拟合曲线求其曲率，由于两段函数连接处的曲率最大，故将这个点作为福安特性曲线的“拐点”[2-5]。

1.2 光电效应测定普朗克常量实验数据

本实验数据利用YGP-2型普朗克常量实验装置测量得到，光电管阴极采用石英侧窗不透明锑钾铯材料，数据如表1所示：

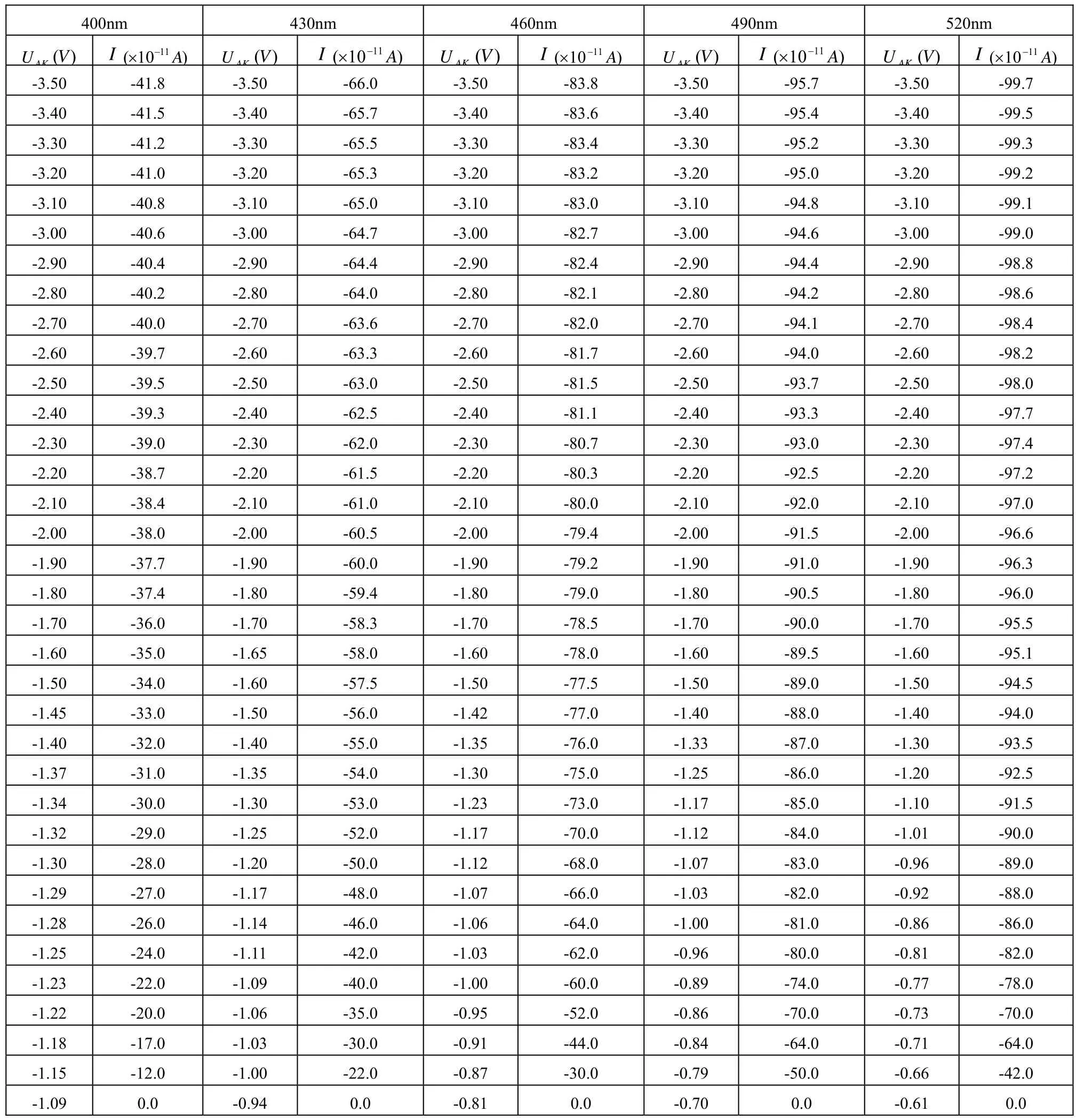
表1 光电效应测定普朗克常量实验数据

2 光电效应曲率法的Matlab设计

2.1 曲率法主要程序

基于上述原理，编制Matlab程序，源程序主要程序段如下[6]：

y1=a3(1)*x.^3+a3(2)*x.^2+a3(3)*x+a3(4); % x为AKU电压，y1为I光电流。

k2=diff(y1,2); k2=abs(k2);k2=[k2 0]; %拟合数据，并求曲率半径

k1=diff(y1,1);

k=k2./((1+k1.^2).^(3/2));

kk=subs(k); kk=double(kk); %kk为双精度曲率半径

n=length(kk);

mk=max(kk);

for i=1:n

if kk(i)==mk

fprintf('400nm波长对应截止电压是(单位 ℃)： %d. ');

disp(vpa(x(i),4))

X=x(i); %最大斜率值对应x值

end

end

利用程序对表1中不同波长数据进行处理，分析得出各波长的截止电压，如图2所示：

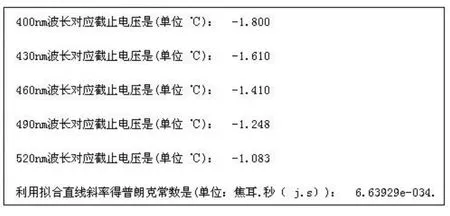
图2 光电效应数据处理程序运行结果显示

同时，可将各截止电压与对应光线频率进行线性拟合，拟合结果，如图3所示：

图3 截止电压-频率拟合曲线

由原理可知拟合曲线斜率k与电子电量e的乘积就是普朗克常量h。

2.2 曲率法确定普朗克常量的注意点

利用曲率法处理光电效应确定普朗克常量数据时，由于测量的数据点个数有限，拟合时的参数（拟合阶数、数据间隔选取等）都会影响到普朗克常量的处理结果，如图4、图5所示：

图4 处理参数设置不合理时光电效应数据处理程序运行结果显示

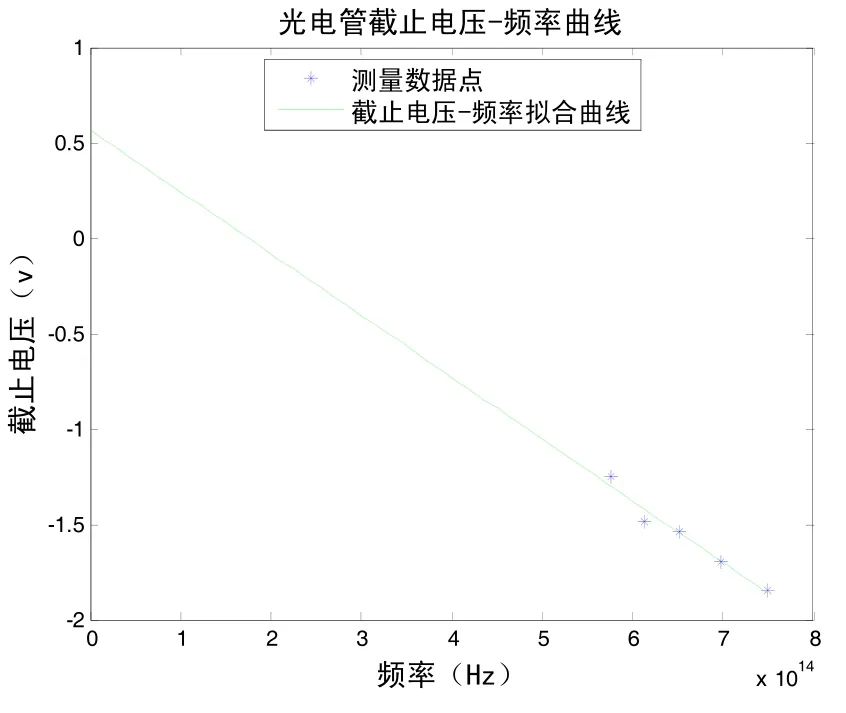
图5 处理参数设置不合理时截止电压-频率拟合曲线

参数设置不合理的运行结果及截止电压-频率拟合曲线（此时普朗克常量为的相对误差已经达到21.77%）。此时可以看到图5上的各截止电压点到拟合直线上的误差明显要大于图3上的情况，所以利用曲率法得到准确的普朗克常量的关键是适当调整参数，使各截止电压在拟合曲线按最小二乘原理分布，且误差要为最小。这点在实际应用中必须予以注意，以得到准确结果。

3 总结

利用Matlab对测量数据进行分析、处理其结果可以有较高的精确度。本文所给出的用Matlab处理光电效应确定普朗克常量的曲率法，在实际应用中与理论值具有很高符合度。其处理难度亦大大小于手工拟合，为快速测定普朗克常量提供了一种有效的方法。

[1] 姚启钧.光学教程[M].高等教育出版社,2002.

[2] 穆翠玲.光电效应实验的计算机采集与数据处理[J].实验室研究与探索.2010,29(8):226-229.

[3] 章佳伟, 殷士龙.在光电效应实验中用曲率法测普朗克常量[J].物理实验，2003，23(11):42-44.

[4] 闻春敖,郑晓东.光电效应法测量普朗克常数的数据处理及误差分析[J].光学技术,2009,(35):191-193.

[5] 白光富,等.光电效应测普朗克常数新数据处理方法[J].物理与工程,2013,23(3):4-8.

[6] 王沫然.MATLAB与科学计算[M].电子工业出版社,第二版,2005.

The Processing Design of Planck's Constant Photoelectric Effect By Matlab

Wang Yunjie1, Sun Yan2
(1.Qinghai Normal University, Physics Department, Xining810008, China; 2. Qinghai University for Nationalities, Department of Computer Science and Technology, Xining810007,China)

An application of curvature approach to measuring photoelectric effect Planck constant was introduced. The processing program was designed by Matlab, and Experimental data were processed by this processing method. Meanwhile, the attention points in processing course were elaborated. The results showed that this method had high accuracy, the problem of hard decision on cut-off voltage and bigger errors were solved.

Planck's Constant; Cut-Off Voltage ; Matlab; Curvature Method

TP311

A

1007-757X(2014)10-0008-03

2014.04.24）

国家自然科学基金（51167016）

王蕴杰（1974-），男，河北霸州，青海师范大学物理系，硕士，副教授，研究方向：算法优化、数据分析处理，西宁，810008孙 燕（1973-），女，山东青岛，青海民族大学计算机科学与技术系，副教授，硕士，研究方向：语音信号处理，西宁，810007