基于自相关算法的TOA估计方法研究
孙 超,王世练,朱 江
(国防科学技术大学电子科学与工程学院,长沙410073)
基于自相关算法的TOA估计方法研究
孙 超,王世练,朱 江
(国防科学技术大学电子科学与工程学院,长沙410073)
TOA(脉冲到达时间)估计是检测和截获非合作突发通信信号的关键,在通信对抗中至关重要。在介绍基于自相关(AC)算法TOA估计原理的基础上,讨论了在低信噪比情况下自相关算法的门限设置问题。采用双门限方法对门限设置进行了改进,并通过计算机进行了仿真分析和验证。
自相关算法;脉冲到达时间估计;门限
1 引 言
随着现代通信技术的高速发展,复杂电磁环境中的战场通信手段和技术层出不穷。无线电侦察作为现代战争中的关键环节,其基本任务是对空间通信信号进行搜索、截获和分析。战场突发信号特征未知且缺少先验知识,快速准确的进行TOA估计是检测、截获、破解敌方空间突发信号的关键。
TOA估计最早应用于常规雷达的测距中,由于信号的先验知识已知,因此可以通过接收信号与本地模板信号进行匹配滤波得到TOA估计[1]。在此基础上,Low.Z.N,Cheong.J.H,Law.C.L等论证了匹配滤波方法在超宽带(UWB)雷达视距传输(LOS)应用中TOA估计的可行性[2]。而对于战场突发通信信号,其先验知识基本都是未知的,无法构造本地模板信号,因此匹配滤波的方法不再适用。由于自相关算法与匹配滤波具有等价的效果,文献[3]提出了一种移位N点自相关的方法来进行TOA估计,解决了非合作通信的本地模板信号缺失问题。随着UWB雷达的快速发展和通信接收机的带宽逐渐增大,低于奈奎斯特采样率的采样信号相关性分析已经不能采用常规方法。文献 [4]中D'Amico.A.A,Mengali.U,Taponecco.L提出了一种基于能量检测的TOA估计法。该方法计算量很小,也不需要高速采样信号。文献[5]综合对比分析了匹配滤波、自相关和能量检测几种TOA方法的性能,提出了能量检测的误差理论和一种两步TOA估计法,将能量检测作为粗估计的第一步,结合匹配滤波等算法进行精确TOA估计。由于上述方法均受门限选择的影响,文献[6]提出了一种图像边缘检测的DOB滤波器,利用图像局部边缘的灰度突变进行检测,避免了门限值的选取,并应用于信号处理领域。
以下主要对用于TOA估计的自相关算法进行研究,同时讨论该算法在低信噪比时的门限设置问题,并通过计算机进行仿真分析和验证。
2 算法研究
一般来说,电子侦察机截获通信信号的信号参数基本上都是未知的。因此对于信号的TOA估计,只能从接收信号r(t)入手分析。对于一个有限长信号,其自相关函数一般不会快速衰减,考虑白噪声是随机性很强的一个序列,相邻点之间是独立分布的,其自相关函数为一个冲激响应,只在τ=0时不等于零。因此,基于自相关的分析方法可以成为解决缺少先验知识突发信号的TOA估计思路。
设有长度为M的离散信号,其自相关函数定义为:

从上式也可看出,自相关函数的峰值是接收信号通过一个平方率检波器,再进行能量累积与平均。因此,如果对于一个通信信号加窗,再进行滑动,每次的滑动步长可以取做1,在每个窗内求取信号点的平方和平均值,即可以得到由相对每个点的自相关最大值构成的一条曲线。估计这条曲线的峭度值和峰值,则可以得到TOA估计值。设窗宽为W,信号加窗滑动模式如图1所示:

图1 移位1点自相关法示意图
取m=0时,Crr(0)可以始终取最大值,对信号的累积作用可以达到最强,但同样对于白噪声来说,也会产生平方累积效果。因此对于检测低信噪比下的信号,考虑用Crr(N),而不是Crr(0)。因为对于白噪声而言,考虑噪声采样点间都是独立分布,一般认为噪声的N点自相关函数Cnn(N)=0。
为使窗内的相关次数达到最大,可以取N=1,因为只要N不等于0,都有Cnn(N)=0,而且可以使信号的自相关幅值与最大值的差值较小,尽可能提高信号的累积量,向最佳检测逼近。
以一段线性调频(LFM)脉冲信号为例,相邻点自相关的原理和物理解释如图2所示。

图2 相邻点自相关的物理解释
图2中,首先对线性调频(LFM)脉冲信号加窗进行移位一点自相关计算,再将窗按照步长为1进行滑动,即可得到移位一点的相关输出信号。分析三个在时域上错开的窗,明显可见,窗1进行自相关得到的输出为A点幅度。类似的,窗2为B,窗3为 C点幅度。窗1内整体都是信号,窗2中前段包含信号,窗3则全是噪声,又因为A,B,C点的幅度与每个窗内的自相关函数峰值移位一点后的值相等,因此A>B>C≈0。
下面再通过表达式分析算法的可靠性,假设自由空间接收到的通信信号为r(t)=s(t)+n(t),经过处理变为复数形式:

式中,A为信号幅度,φ为初始相位,f为载频,w(i)为复噪声。其相关函数为:

经过计算推导可得:

其中,NA2ej2πfΔt为信号部分,w′为相关后的噪声。

当窗长足够长时,即M较大时,由中心极限定理可知,w′近似为高斯分布的复噪声。
另外,算法还可以通过迭代递推来实现:

这种方法极大简化了计算复杂度,保证了TOA估计要求的实时性。
接下来将捕获到的一段Link-16数据链信号做移位一点自相关输出,如图3所示。

图3 数据链信号的移位1点自相关输出
图3中左图为淹没在噪声之中的数据链信号,右图为做了自相关后的输出信号。可见算法极大地抑制了噪声并累积了信号能量,如果从右边图像中要提取出Link-16数据链信号的到达时间,理论上只需要确定一个合理的门限,当输出第一次超过该门限值时,即认为是信号到达时间。
但是当信噪比过低时,信号到达后出现的包络改变会变得跟噪声自相关输出相似,这时无论如何选择门限值,都难以正确地估计TOA值,鉴于该情况考虑采用双门限方法,分为以下两步:
第一步:确定检测门限
由于信号中夹杂着噪声,为了准确进行TOA估计,需要提出一种自适应门限,即根据噪声的变化来改变门限。因此,在信号到达之前需要对噪声的标准差进行估计。

式中,ni是未经过复变换的噪声采样值。经过相关运算之后,噪声w′服从N(0,4Nσ4)分布,而在实际中,σ是由来近似,它的幅值服从均值为u,方差为的瑞利分布:

在一定虚警概率的前提下,可得出噪声下的检测门限为:

其中,a是检测因子,由具体的虚警概率确定,一般情况下,a的取值为2-10。
第二步:为了排除噪声引起的抖动,在得到检测门限后,判断超过门限的m个点,如果有n=βm个点都超过门限,即认为在这m个点中的第l个点为信号的到达时刻。当自相关输出低于门限值后,相应地,如果m个点中有n个点低于门限,就认为m个点中的第l′个点为信号的结束时刻。这样,不仅可以得到较为准确的TOA估计,还能估计出信号的长度。
综上,基于自相关算法的TOA估计流程图如图4所示。
3 仿真验证
仿真环境:信号采样率为3KHz,信号采用BPSK调制,载频为600Hz,码元符号率为30Hz,信号起始时间为333ms,结束时间为666ms,整段接收信号(含噪)截取长度为1s,自相关窗长选为16ms,滑动步长为3ms,信噪比分别取为20dB,10dB,5dB。可以得出图5-图7的结果。
从仿真结果可以看出,在中高信噪比下,移位1点自相关估计具有较好的估计效果。在SNR=20dB时,自相关输出波形基本上为一矩形窗,上升沿陡峭,抖动较少,估计出的TOA基本上与信号真实TOA值接近。当SNR下降到10dB时,自相关输出的上升沿仍保持良好,只是在脉内抖动较大,经过选择合适的门限,也可得到良好的TOA估计值。而当SNR=5dB时,在时域上已经难以区分信号和噪声,自相关输出整体抖动较为明显,估计出来的TOA值误差较大,但是也能经过修正得到一定误差的TOA值。若SNR进一步下降,如图8所示,当SNR=0dB时,自相关输出波形会出现整个时域内抖动的情况,信号到达后出现的包络改变变得跟噪声自相关输出相似,就会导致无论如何选择门限值,都难以正确地估计TOA值。

图5 SNR=20dB的AC-TOA估计

图6 SNR=10dB的AC-TOA估计
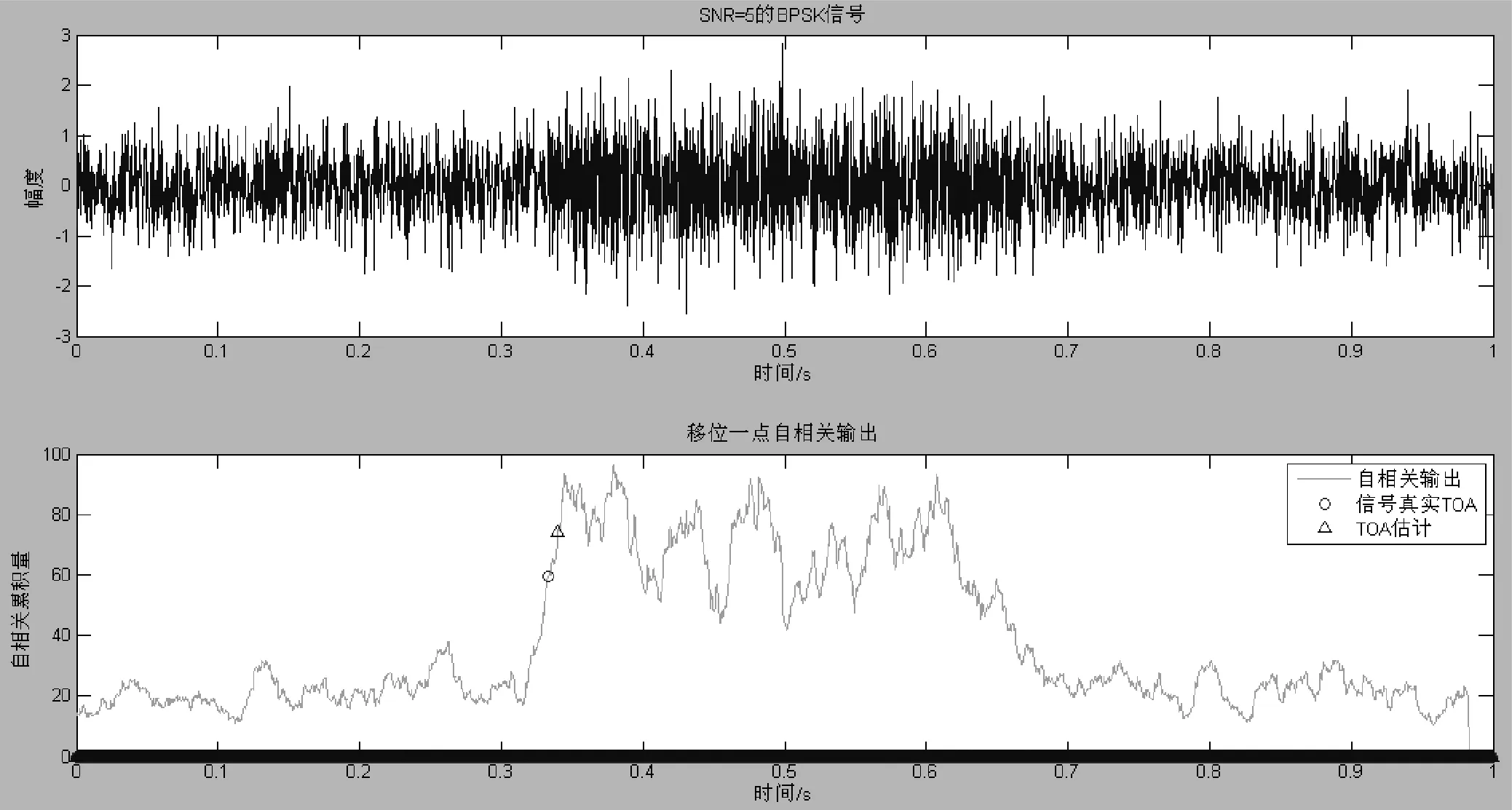
图7 SNR=5dB的AC-TOA估计

图8 因信噪比过低引起的TOA误判
如图8,虽然选取的门限与真实信号到达时输出的自相关幅度相近,但信号真实的TOA值为333ms,而估计器在120ms的位置就已经到达门限,属于虚警误报,这种误差极大的估计是毫无意义的。因此采用双门限的方法,仿真结果如图9所示。

图9 经过双门限改进后的TOA估计
由图9可以看出,经过第一检测门限,再利用第二判断门限进行TOA估计后,减小了虚警导致TOA误判的可能性,TOA估计值不会再出现于频繁抖动的噪声相关输出中,改善效果明显。
4 结束语
以上研究了基于自相关算法的TOA估计方法,并通过计算机进行了仿真分析。仿真结果表明,在高信噪比下,采用移位1点自相关估计方法具有较好的估计效果,估计出的TOA基本上与信号真实TOA值接近。在中信噪比下,通过选择合适的门限,也可得到良好的TOA估计值。而当信噪比较低时,需要对门限设置进行改进,经过双门限检测判断后,减少了因信噪比过低引起的TOA误判问题。
[1]刘少成.电子侦察信号实时检测算法及其应用[D].西安电子科技大学,2011.
[2]Low ZN,Cheong JH,Law C L,etal.Pulse detection algorithm for line-of-sight(LOS)UWB ranging applications[J].Antennas and Wireless Propagation Letters,IEEE,2005(4):63-67.
[3]席轶敏,刘渝,靖晟.电子侦察信号实时检测算法及性能分析[J].南京航空航天大学学报,2001,33(3):277-281.
[4]D'Amico A A,Mengali U,Taponecco L.Energy-based TOA estimation[J].Wireless Communications,IEEE Transactions on,2008,7(3):838-847.
[5]Guvenc I,Sahinoglu Z,Orlik P V.TOA estimation for IRUWB systems with different transceiver types[J].MicrowaveTheory and Techniques,IEEE Transactions on,2006,54(4):1876-1886.
[6]A Rosenfeld,M Thurston.Edge and curve detection for visualscene analysis[J].IEEE Transaction on Computers,1971(20):562-569.
Research of TOA Estimation Based on Auto-correlation Algorithm
SUN Chao,WANG Shi-lian,ZHU Jiang
(School of Electronics Science and Engineering,National University Defense Technology,Changsha 410073,China)
The estimation of time of arrival(TOA)of impulse signal is the key point for detection and interception of burst and non-cooperative communication signals,and it is very important for communication countermeasure.Based on a introduction of the AC-TOA,a detailed discussion about the threshold setting of AC-TOA in low SNR is presented,by using the method of double threshold,the improvement to the threshold setting is conducted.Finally,the performance of the algorithms is verified by computer simulation.
Auto-correlation Algorithm;TOA estimation;Threshold
10.3969/j.issn.1002-2279.2014.04.013
TN911.7
:A
:1002-2279(2014)04-0039-05
孙超(1985-),男,新疆乌鲁木齐人,工程硕士在读,主研方向:无线通信对抗。
2013-12-25

