一种基于量子进化算法改进的k-mean聚类算法❋

张睿哲，杨照峰，赵伟艇

（1.平顶山学院计算机科学与技术学院，平顶山467002；2.平顶山学院软件学院，平顶山467002）

一种基于量子进化算法改进的k-mean聚类算法❋

张睿哲1，杨照峰2，赵伟艇2

（1.平顶山学院计算机科学与技术学院，平顶山467002；2.平顶山学院软件学院，平顶山467002）

聚类分析是模式识别中的一个重要问题，是非监督学习的重要方法。K-means算法是其中最经典的聚类算法之一。但是这种方法面对大规模数据的时候工作量非常巨大，并且保证不了聚类结果的最优性。提出了一种基于量子进化算法的改进的K-means聚类算法。该方法结合了两个方法的优点，用量子进化算法进行优化，并且改进了量子进化算法中的交叉算子和更新算子，提高了基于量子进化算法的K-means算法局部搜索能力。实验结果表明，改进算法取得了较好的效果。

量子进化算法；聚类算法；量子计算；数据挖掘；进化优化

1 引 言

聚类分析是模式识别中的一个重要问题，是非监督学习的重要方法［1］。聚类分析的目标是将一个数据集划分成若干个簇.使同一个簇中的对象尽可能地相似，而不同簇对象间的差异尽可能的大。聚类分析是通过无监督训练将样本按相似性分类［2］。

聚类分析根据基因功能对其进行分类以获得对人群中所固有结构更深入的了解。可以帮助市场人员发现顾客群中存在不同特征的组群［3］。聚类还可以从地球观测数据库中帮助识别具有相似土地使用情况的区域。聚类分析是一种典型的组合优化问题，目前已有很多种聚类算法，主要分为［4］：划分聚类、基于密度的聚类以及基于网格的聚类、层次聚类。划分聚类中的K-means算法是其中最经典的聚类算法之一。该聚类算法首先根据一定的经验准则选取某些聚类参数，但是这种方法面对大规模数据的时候工作量非常巨大，并且保证不了聚类结果的最优性。所以需要寻找一种能克服K—mean对初始化敏感这一缺点的全局优化算法。

提出了一种基于量子进化算法的改进的K-means聚类算法。该方法结合了两个方法的优点，用量子进化算法进行优化，并且改进了量子进化算法中的交叉算子和更新算子，提高了基于量子进化算法的K-means算法的局部搜索能力。实验结果表明，改进算法取得了较好的效果。

2 k-mean算法简介

首先，随机地选择k个对象，每个对象初始地代表了一个簇的平均值或中心。对剩余的每个对象，根据其与各个簇中心的距离，将它赋给最近的簇。采用平方误差函数的k-mean算法流程如下：

输入：簇的数目k和包含n个对象的数据库。

输出：k个簇，是平方误差函数最小。

方法：

（1）任意选择k个对象作为初始簇中心；

（2）repeat

（3）根据簇中对象的平均值，将每个对象重新赋给最类似的簇；

（4）更新簇的平均值，即计算每个簇中对象的平均值；

（5）until不再发生变化。

设目标函数：

其中，聚类中心

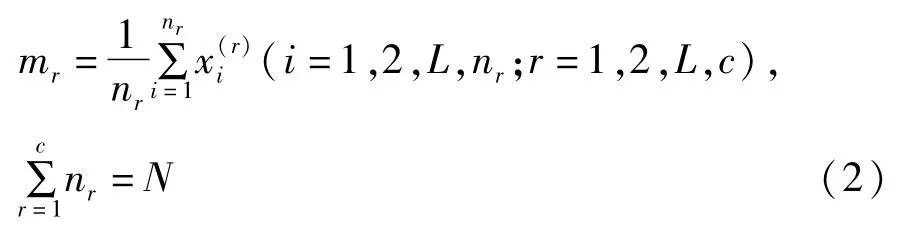
nr为属于r类的样本（记录）个数；

N为样本（记录）数；

c为聚类中心数（2≤c≤N-1）。

3 基于量子进化算法改进的聚类算法

近几年来，一些学者研究将量子计算的概念引入进化算法和多目标进化算法中，从而提出诸多量子进化算法（Quantum-inspired Evolutionary Algorithms，QEA）［5-6］。

3.1 染色体构造

用a＝（a1，a2，...，aN）表示遗传算法的染色体结构，用染色体来动态确定聚类数目。例如，设染色体长度为6，那么，当染色体为｛1，2，1，3，2，1｝，聚类数目c为3；当染色体为｛1，4，1，6，4，1｝，聚类数目c为3；当染色体为｛1，5，1，3，2，1｝，聚类数目c为4。

Step 0：设置遗传算法的相关参数，max_gen：最大迭代次数；pop_size：群体大小；l_chrom：染色体长度；pc：交叉概率；pm：变异概率；c：初始聚类数目；w：在评价函数中的参数；gen＝0。

3.2 群体初始化

群体初始化是遗传算法最基本的步骤。从待分类的点中随机选择K个点作为问题的一个解并编码为一个染色体。重复进行这个操作，直到pop_size（种群的大小）个染色体全部被初始化。

Step 1：群体初始化

for i＝1 to pop_size do

for j＝1 to l_chrom do

染色体ai的第j位等位基因＝random（0，c）；

endfor

endfor

3.3 适应度函数设计

使用类内距与类间距之和作为目标函数，即：

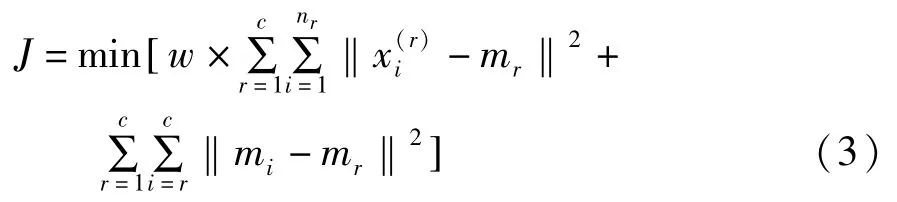
其中，w为权重，它反映决策者的偏好。当w变大时，聚类数目c也增大；反之，c将减小。算法的目的是搜索J值最小的聚类中心，因此适应度函数为：1／J。

3.4 量子门更新策略

算法中采用量子旋转门U（Δθ）更新个体，U（Δθ）定义如下［7］：

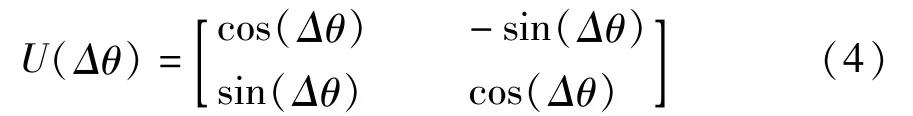
其中，Δθ为旋转角，Δθ的具体计算如下：

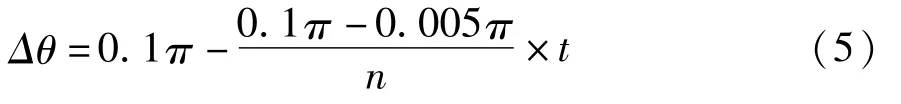
其中t为进化代数。

4 实验结果与分析

为了验证上述算法的有效性，实验数据分为两组，第一组为某一数据库中的记录，第二组为Fisher的Iris植物样本数据。对两组数据分别使用K-mean算法和本文提出的遗传聚类算法进行实验。改进的算法有关参数设置如下：初始 c＝12、a＝0.2、pop_size＝30、k1＝k3＝0.9、k2＝k4＝0.1、gen_max＝1000。运行100次的平均收敛代数分别为163代和372代。实验结果如表1所示。

表1 数据1的实验结果

第二组数据是Fisher的Iris植物样本数据，该数据由分别属于三种植物的150个样本组成，每个样本均为四维模式向量，代表了植物的四种特征数据。用两种算法分别做了3次实验，实验中遗传算法的pop_size＝100，每次实验的迭代次数为100次，其他参数不变，实验结果如表2所示。

表2 数据集Iris的实验结果

可以看出普通的K-mean算法对初值敏感，并且在三次运行中均收敛于不同的局部极优点。而本文改进的K-mean算法每次均能收敛到全局最优点。这表明了本文改进的K-mean算法与普通的K均值算法相比，具有较强的全局收敛性能。

5 结束语

提出了一种基于量子进化算法的改进的K-means聚类算法。该方法结合了两个方法的优点，用量子进化算法进行优化，并且改进了量子进化算法中的交叉算子和更新算子，提高了基于量子进化算法的K-means算法的局部搜索能力。实验结果表明改进算法取得了较好的效果。

［1］於跃成，王建东，郑关胜，等.基于约束信息的并行k-means算法［J］.东南大学学报（自然科学版），2011，41（3）：505-508.

［2］陆林华，王波.一种改进的遗传聚类算法［J］.计算机工程与应用，2007，43（21）：170-172.

［3］傅涛，孙亚民.基于PSO的k-means算法及其在网络入侵检测中的应用［J］.计算机科学，2011，38（5）：54-55，73.

［4］吴夙慧，成颖，郑彦宁，等.K-means算法研究综述［J］.现代图书情报技术，2011，205（5）：30-35.

［5］Tony H.Quantum computing：all introduction［J］.Computing＆Control Engineering Journal，1996，10（3）：105-112.

［6］Narayanan A，Moore M.Quantum-inspired genetic algorithm［A］.Proc of IEEE International Conference on Evolutionary Computation［C］.Piscataway：IEEE Press，1996：61-66.

［7］Kuk-Hyun Han，Jong-Hwan Kim.Genetic Quantum Algorithmand its Application to Combinatorial Optimization Problem［C］.Proceedings of the 2000 Congress on Evolutionary Computation，2000：1354-l360.

An Im proved K-mean Clustering Algorithm Based on Quantum Evolutionary Algorithm

ZHANG Rui-zhe1，YANG Zhao-feng2，ZHAOWei-ting2
（1.Computer Science and Technology Academy，Pingdingshan University，Pingdingshan 467002，China；2.School of Software Engineering，Pingdingshan University，Pingdingshan 467002，China）

The cluster analysis is a key point in pattern recognition and an important method of unsupervised learning.The K-means algorithm is one of themost classical clustering algorithms，which produces huge workload from themassive data and cannot ensure the optimality of the clustering results.This paper proposes a quantum evolutionary algorithm based on improved K-means clustering algorithm which combining such advantages as optimized quantum evolutionary algorithm，the improved crossover operator and update operator in quantum evolutionary algorithm for improving the quantum evolutionary algorithm based on K-means algorithm local search ability.The experimental results show that the improved algorithm achieves good effect.

Quantum evolutionary algorithm；Clustering algorithm；Quantum computing；Data mining；Evolutionary optimization

10.3969／j.issn.1002-2279.2014.04.023

TP393

：A

：1002-2279（2014）04-0071-03

河南省科技计划重点项目（102102210416）

张睿哲（1971-），男，河南舞钢人，讲师，硕士，主研方向：计算机应用技术、网络管理体系结构与管理机制方面的研究。

2014-01-16