一种适合卫星通信的宽带频谱感知算法
张要,李勇,程伟
一种适合卫星通信的宽带频谱感知算法
张要,李勇,程伟
在卫星通信系统中实现认知无线电技术需要对多频带的宽带信号进行频谱感知。针对使用传统OMP(Orthogonal Matching Pursuit)算法在宽带调制转换器(Modulated Wideband Converter,MWC)系统下,出现的由于相邻两个支撑频带间距太近而出现遗漏支撑频率的现象,提出一种基于邻近搜索的OMP改进算法,仿真表明,该算法能够更优化地实现信号的重构,保证频谱检测维持较高的检测概率。
卫星通信;频谱检测;临近搜索
0 引言
认知无线电作为一种更智能的频谱共享技术,能够感知无线通信环境,自适应地改变系统工作参数,动态地检测和有效地利用空闲频谱。认知无线电最为基础和关键的一步是频谱感知,了解干扰源所在频段并有效避让要求通信双方对频谱环境进行检测。作为地面通信的补充,卫星移动通信已经在人们日常生活中广泛应用,目前卫星移动通信系统主要集中在100MHz~3GHz这一范围[1],而这一范围恰是地面通信应用重点区域,通过认知无线电技术,多用户之间能够提高频谱利用率,而且在突发干扰下能够互相躲避,因此设计一个适合空间通信的频谱分析算法非常重要。
根据认知无线电理论,卫星通信系统能够自组织的进行感知和组网,卫星节点需要感知很宽的频段。宽带频谱感知要求对数 GHz 的带宽进行检测,过高的采样速率和数据量对现有的硬件设备提出了巨大的挑战。处理宽带感知的基本的方法有:宽带直接感知、串行分段感知、并行分段感知。这些基本的宽带频谱感知技术硬件实现成本较高,且受制于目前实际的无线电系统射频前端性能。针对宽带信号的采样和分析,认知用户需要采用更高速的ADC和数字信号处理器(Digital Signal Processor, DSP),功耗和代价较大。如何降低宽带频谱感知的实现复杂度是目前重点关注的问题,而压缩感知(Compressed Sensing, CS)的提出为上述问题的解决提供了一种可行的思路。经典的Nyquist采样定理指出,在信号的采集的过程中,必须以至少两倍于信号最高频率的采样率获得采样值。但是随着数字技术的发展,一些已有的窄带频谱感知研究方法[2]包括能量检测法、匹配滤波器法以及循环平稳特性检测法等并不适合宽带移动卫星通信系统。面对星间通信中信道占用呈现的稀疏状态,以低速率采样和运算是简化设备的必要途径。
压缩感知理论于2006年被提出后[3],迅速成为了信号处理领域的研究热点。按照压缩感知(Compressive Sampling,CS)理论,我们不必对N维信号x直接采样,取而代之的是以维的测量矩阵对原信号进行线性测量。压缩感知的基本模型如图1所示:

图1:压缩采样基本模型框图
与传统的压缩方法相比, CS是将压缩和采样结合成一步进行,利用信号稀疏性,以远低于Nyquist采样率的速率对信号进行测量编码,测量过程是对源信号的一个全局观测,每一次采样都包含了信号所有样本函数的少量信息,而并非采样信号本身。解码过程是通过合适的重构算法来进行恢复源信号,且观测信号y中丢失少量元素信息对重构影响不大。
1 宽带调制转换器压缩采样系统
宽带调制转换器(MWC)[4]是一种适合卫星通信的无线感知方案。与众多压缩采样系统相比,MWC有如下几个特点:(1).系统可以对高频宽带多频段模拟信号进行压缩采样;(2).采样系统不需要频段位置分布的先验信息;(3).系统可以通过现有的模拟设备与ADC(低采样率)实现。由于MWC在这些方面具有的独特优势,使得其成为卫星通信环境下,实施频谱感知时,前端采集所需感知数据时采用的最适合的方法。调制宽带转换器采样系统的示意图如图2所示:

图2:调制宽带转换器压缩采样系统





2 信号重构框架描述
信号重构的目的是从压缩采样得到的M维采样信号中恢复N维的稀疏信号S,由于M< 图3:信号重构模块 令 在信号重构框架中,将无限测量向量(IMV)问题转换到有限多测量向量(MMV)问题之后,需要对进行求解,得到频率支撑集S 。通常这一求解采用贪婪追踪算法:最常用的一种便是正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法,和MP算法一样,OMP同样需要在每次迭代的过程中将待分解的信号与每次迭代选择矩阵中的每一个原子做内积运算,寻找内积结果最大的原子,即与待分解信号最匹配的原子。所不同的是,OMP算法在分解的每一步中都需要对已经选择的全部原子做正交化处理,从而保证了迭代的最优性。 由于MWC压缩感知框架本身的特性,使用OMP算法会出现由于相邻两个支撑频带间距太近而出现遗漏支撑频率的现象,所以提出一种基于邻近搜索的改进OMP算法,在每次搜索出的支撑频段结果的附近进行二次搜索,最终实现搜索结果的优化。改进后的算法主要步骤如下: 算法主要过程: 2) 求解优化问题找到一个支撑频带的估计值: 通过MATLAB仿真构造一种模拟卫星多频带接收的的宽带感知信号,我们可以得到无线感知的首要感知对象:多频带的高频宽带信号源。原始宽带信号定义如下: 假设一段由4个非重叠频带信号构成的宽带信号,子带信号带宽50 MHz,总频谱带宽存在于5 GHz范围之内,这使得奈奎斯特频率为10GHz。采用MWC方案的压缩感知:利用50路的低速采样通路,每路采样速率 51.3MHz。假设接收到的原信号受到加性高斯白噪声的污染。在信噪比20db下,原信号、带噪信号以及重构信号时域图如图4所示: 图4:信噪比20db下原信号、带噪信号和重构信号时域图 由于模拟的卫星通信频段,所以与地面通信的频段不同,其波段往往在数G Hz.。对这样的信号由于实际器件的限制往往无法在射频进行采样,通过本方案设计的压缩采样和感知方法,通过对原信号和重建信号频谱分析,可以看出在一定的噪声条件下,经过压缩感知之后的重建信号能够保存原信号中的重要信息,使得其在频域内的关于频谱感知的重要信息没有丢失。通过频域内的重建信号可以看出:其频谱与原信号能够很好的对应。频谱除了在绝对幅度方面有所失真之外,其相对幅度和频点位置都能够有效获取,这也是卫星群通信环境下的进行频谱感知所关心的最重要的信息,获得这些信息之后就能够有效得到星群环境下的频谱占用和功率情况。另外采用带有邻近搜索的新算法,能够确保距离比较接近的频率分量不被漏掉。在信噪比20db下,原信号、带噪信号以及重构信号的频域图如图5所示: 图5:信噪比20db下原信号以及重构信号频域图 通过MATLAB仿真实验来考察新算法的重构性能,实验中采用个子带信号,每个信号的带宽均为50MHz,载频且随机选取,采样系统中各通道的混合函数以均匀分布随机产生。实验中采用重构成功率来评价算法的重构性能,重构成功的定义为:估计与真实的支撑集分别为和,当且矩阵A的子矩阵列满秩,则称为成功重构。通过20次Monte Carlo实验,得到重构成功率统计结果。由于成功的重构支撑集之后,可以在频域内有效的恢复宽带信号的频率分量信息,实现成功的频谱检测。所以其重构成功率可以反映系统进行频谱感知的检测概率。 图6:不同信噪比下重构信号相对误差对比图 这是因为新算法为了保证不发生支撑频带的检测遗漏,采用邻近搜索后可能的得到了超过原信号支撑频带数量的结果,这就使得重构误差增加。但同时,由于卫星通信中的无线频谱感知,更关注的是频谱占用情况,所以检测到频谱的占用情况是考察的首要指标,即确保通信环境中存在的通信频带占用状态不被检测所遗漏。 采用OMP算法与改进后新算法的频谱检测概率随系统信噪比的变化曲线如图7所示: 图7:不同信噪比下重构算法检测概率对比图 从图中我们可以看出,当信噪比为20db时,新算法即可以达到1的重构概率(100%),而原算法仅能达到0.8的检测概率(80%),所以新算法以信号重构误差少量增加为代价,使得系统能在低信噪比环境下,能够保证频谱检测维持较高的检测概率。 随着认知无线电的不断发展,对频谱感知技术提出了更高的要求。为了更好地找到适合于空间卫星通信的频谱感知算法,本文提出了一种MWC压缩采样系统下的改进OMP算法,通过计算机仿真可以看出:重构信号频谱与原信号能够很好的对应,除了在绝对幅度方面有所失真之外,其相对幅度和频点位置都能够有效恢复,确保信号的频率分量不被遗漏,这也是卫星群通信环境下的进行频谱感知所关心的最重要的信息。另外采用这一新算法,还能够确保距离比较接近的频率分量不被漏掉,实验表明该算法对卫星通信环境下的宽带信号频谱感知有很好适用性。 [1] ZHANG Geng- xin, ZHANG Hang. Satellite Mobile Communication Sysem[M] . Beijing: People’s Posts & Telecommunications Press, 2001. ( in Chinese) [2] Haykin S. Cognitive Radio: Brain - Empowered Wireless Communications [ J] . IEEE Journal on Selected Areas in Communications, 2005, 23( 2) : 201- 220. [3] E. Candès, J. Romberg, Terence Tao. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. [j]IEEE Transactions on Information Theory, 2006, 52(2): 489~50 [4] Mishali M, Eldar Y C. From theory to practice: Sub-Nyquist sampling of sparse wideband analog signals [J]. 1EEE Journal of Selected Topics in Signal Processing, 2010, 4⑵:375-391. [5] Mishali M, Eldar Y C. Expected RIP: Conditioning of the modulated wideband converter[C],IEEE Information Theory Workshop, 2009. ITW 2009.. IEEE, 2009: 343-347. [6] Mishali, M.,Eldar. Y. C.Blind multi-band signal reconstruction: Compressed sensing for analog signals. [j]IEEE Transactions on Signal Processing, 2009, 57(3): 993~1009. A Broadband Spectrum Sensing Algorithm in Satellite Communication Zhang Yao,Li Yong,Cheng Wei Cognitive radio technology in the satellite communication system requires a multi-band wideband signal spectrum sensing. When applying traditional OMP algorithm in MWC system, a phenomenon of missing supporting frequency appears,which is caused by close distance between two adjacent supporting bands .To solve this problem, an improved algorithm based on proximity search of OMP is proposed. Simulation results show that the algorithm can better achieve the signal reconstruction and ensure keeping high probability of detection in spectrum sensing. Satellite Communication;Spectrum Detection;Proximity Search TN927 A 1007-757X(2014)01-0001-04 2013.12.09) CAST创新基金项目 张要(1990-),男,浙江温州人,西北工业大学,硕士研究生,研究方向:认知无线电频谱感知,西安,710129李勇(1962-),男,陕西人,西北工业大学,教授,博士生导师,研究方向:信号与信息处理技术,西安,710129程伟(1980-),男,陕西志丹人,西北工业大学,讲师,研究方向:无线通信与自组织网络,西安,710129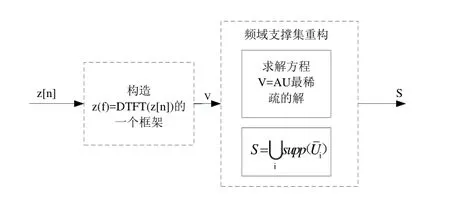
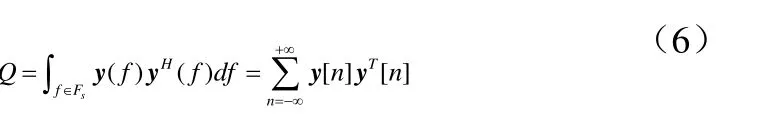

3 基于邻近搜索的OMP算法
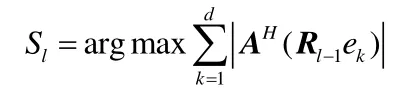
4 仿真实验


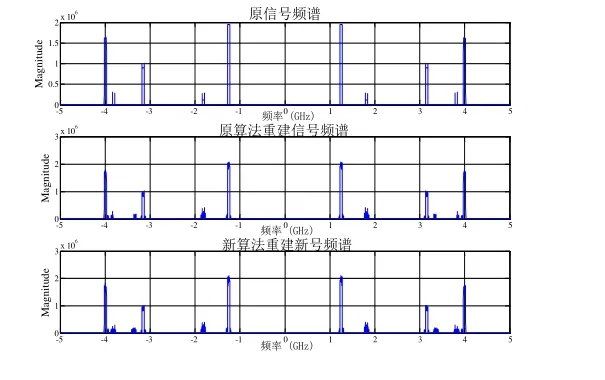


5 总结
(Northwestern Polytechnical University,Xi’an 710129,China)

