大型单轴离心振动台的复合控制策略
罗中宝,杨志东,陈良,丛大成
(哈尔滨工业大学机电工程学院, 150001, 哈尔滨)
大型单轴离心振动台的复合控制策略
罗中宝,杨志东,陈良,丛大成
(哈尔滨工业大学机电工程学院, 150001, 哈尔滨)
针对离心振动台中轻柔基础与上平台间的动态耦合及各非线性因素使系统性能恶化的问题,在传统伺服控制策略的基础上提出了一种复合控制策略。根据耦合等效模型设计几何解耦控制器,以消除轻柔基础与上平台间的动态耦合;综合考虑各非线性因素对系统性能的影响,提出了基于鲁棒控制的反馈控制器和基于两自由度控制的前馈控制器来保证系统的稳定性和控制精度;引入负载干扰力补偿控制器,以减小负载动态特性变化对系统性能的影响。仿真结果表明,经前馈、反馈校正和几何解耦后,离心振动台的频宽已提高至250Hz,完全满足伺服控制策略的频宽要求。经负载干扰力补偿后,在负载特性剧烈下降阶段位置闭环的超调量和调整时间已减少至未采用补偿的50%,且在负载特性随机波动阶段位置闭环的波形失真也得到了显著改善。
离心振动台;几何解耦控制器;鲁棒控制;两自由度控制策略
岩土材料的动态特性都具有很强的非线性,这些特性与岩土应力密切相关,而离心机可提供一个离心加速度场来补偿物理原型的自重应力,通过对岩土自重应力的补偿,便可用小比例尺岩土模型来精确模拟实际岩土原型在地震激励下的响应[1-2]。离心振动台位于离心机上,这也为其研制带来了诸多挑战:①受离心机装机容量的限制,振动台基础(吊篮)的质量和刚度有限,造成轻柔基础-液压动力机构-岩土模型间的动态耦合;②受离心振动复合环境的影响,电液伺服系统核心控制元件——三级电液伺服阀的动态特性将发生变化;③实验时振动台上的两个高压蓄能器被作为短时激振的油源,油液从高压蓄能器中流出,造成油源压力的降低;④岩土模型在地震波的激励下,其自身的动态特性也发生改变。简单分类可将以上4方面挑战归结为如下3个研究热点:①耦合特性分析、解耦控制问题;②非线性因素的抑制问题;③负载干扰力的补偿控制问题。
耦合特性分析的主要任务是阐明轻柔基础、岩土模型对液压动力机构动态特性的影响;解耦控制问题的重点是如何将上平台的绝对运动参考转化为轻柔基础与上平台间的相对运动参考。对于耦合特性分析问题,Conte等详细推导了基础柔性、负载动态对振动台动态特性的影响[3]。作者以离心振动台为研究对象,阐述了该振动台中的耦合特性[4]。对于解耦控制,普通振动台并未涉及,该部分是复合控制策略研究的重点。
非线性因素的抑制问题是在综合考虑各非线性因素的基础上,提出一种能同时保证离心振动台稳定性和控制精度的控制策略。一般来说,为了减小非线性因素对振动台性能的影响,一般采用自适应、鲁棒控制策略或自适应鲁棒复合控制策略。对于自适应控制而言,最具代表性的是由Stoten提出的基于最小控制综合(minimal control synthesis,MCS)的控制策略。Stoten等针对日本E-Defense振动台中存在的非线性、参数变化等问题,提出了一种基于最小控制综合的前馈最小控制综合算法[5]。Gizatullin等将该最小控制综合方法推广至多轴振动台[6]。与此同时,国内外也有很多成功将鲁棒控制策略应用于振动台控制的先例。Cuyper等在传统离线迭代技术的基础上引入基于鲁棒控制的实时控制器来提高离线迭代技术的收敛速度和收敛精度[7]。Vaes等将文献[7]中的控制方法扩展至多轴振动台,也取得了显著成果[8]。对于复合控制策略,Uchiyama等在电动振动台中引入两自由度控制策略(2-DOF control),其中采用μ综合方法设计了两自由度控制中的反馈控制器,在前馈补偿部分引入自适应滤波器来进一步提高振动台的控制性能[9]。对于离心振动台而言,其复现的是“短时高频”的地震波,持续时间仅为1s左右,自适应控制策略很难做到收敛。因此,本文引入鲁棒控制来设计系统的反馈控制器,达到保证系统稳定性的目的;然后引入基于两自由度控制策略的前馈补偿控制技术进一步提高离心振动台对高频参考信号的复现能力。
负载干扰力补偿控制的途径是采用一种控制方法来减小负载动态特性变化对系统性能的恶化。Iwasaki等针对非线性试件提出了一种基于干扰力观测器的反力补偿机制,经验证明该方法可显著提高振动台对地震波的复现精度[10]。Uchiyama等将该反力补偿机制应用于负载为装水容器的电动振动台中[11]。本文将负载力干扰力补偿控制引入到离心振动台中,用以提高振动台对岩土模型动态特性变化的抵抗能力。
1 单轴离心振动台简介
图1所示为哈尔滨工业大学与中国地震局工程力学研究所联合研制的单轴离心振动台。该单轴离心振动台的最大振动负载为1350kg,最大振幅为12 mm,最大水平加速度为30g,最大振动频率为350Hz。与普通振动台、小型离心振动台相比,该单轴离心振动台在结构上做出了如下4点创新和尝试。

1:吊篮;2:上平台;3:凹形运动块;4:橡胶支撑;5:支撑板;6:高压蓄能器;7:液压作动器;8:三级电液伺服阈;9:低压蓄能器
(1)单轴离心振动台采用了新型的冗余驱动技术,即由两套液压动力机构协同完成离心振动台的水平单向激振;考虑到结构的紧凑性,每套液压动力机构均由两条柱塞缸和一台三级伺服阀组成。
(2)普通振动台、小型离心振动台的上平台与液压作动器间的连接多采用球铰。考虑到铰轴的柔性和铰中存在的间隙,传统连接方式并不能满足高频振动的要求。因此,在液压缸与上平台间添加了凹形运动块,这种连接方式可在提高连接刚度的同时减小连接间隙。
(3)支撑导向装置既要支撑平台和岩土模型的高离心力,又要引导它们在指定方向上实现高加速度运动。单轴离心振动台在支撑板与上平台间安装了28个橡胶剪切轴承,用以支撑负载、平台的离心载荷;在水平激振过程中橡胶轴承发生水平向的弹性变形,分析时可将其作为弹性负载考虑。
(4)图1中的吊篮即为离心振动台的反力基础,受离心机容量的限制,吊篮底座的内部做成中空栅格状,最大限度地减小了吊篮的质量,其弹簧刚度也相当有限。普通振动台的反力基础质量一般在负载、平台质量和的15倍以上,单轴离心振动台的该比值不足4∶1。因此,反力基础的动态特性将会对离心振动台性能产生较大影响。
2 单轴离心振动台中的关键问题
2.1 轻柔基础-动力机构-岩土模型的耦合问题
单轴离心振动台的伺服控制策略是通过位置闭环控制来保证上平台的加速度复现精度,而离心振动台中位移传感器反馈的却是上平台、轻柔基础间的相对位移,因此,控制时需将上平台绝对运动参考转化为上平台、轻柔基础间的相对运动参考,其转换关系依赖于轻柔基础-液压动力机构-岩土模型间的动态耦合关系。本文修正了文献[4]中的耦合等效模型,主要是将轻柔基础与上平台的耦合划为运动学耦合和动力学耦合。如图2所示,②中的杠杆表示了上平台与轻柔基础间的运动学耦合,杠杆的比率等于有效负载(上平台与负载)与轻柔基础的质量比;另外,采用①中的一维质量-弹簧-阻尼系统来等效轻柔基础的动态特性。最终,在文献[4]的基础上还考虑了橡胶轴承刚度对系统耦合特性的影响。经推导,上平台、轻柔基础间的相对位移y与伺服阀阀芯位移xv的传递函数
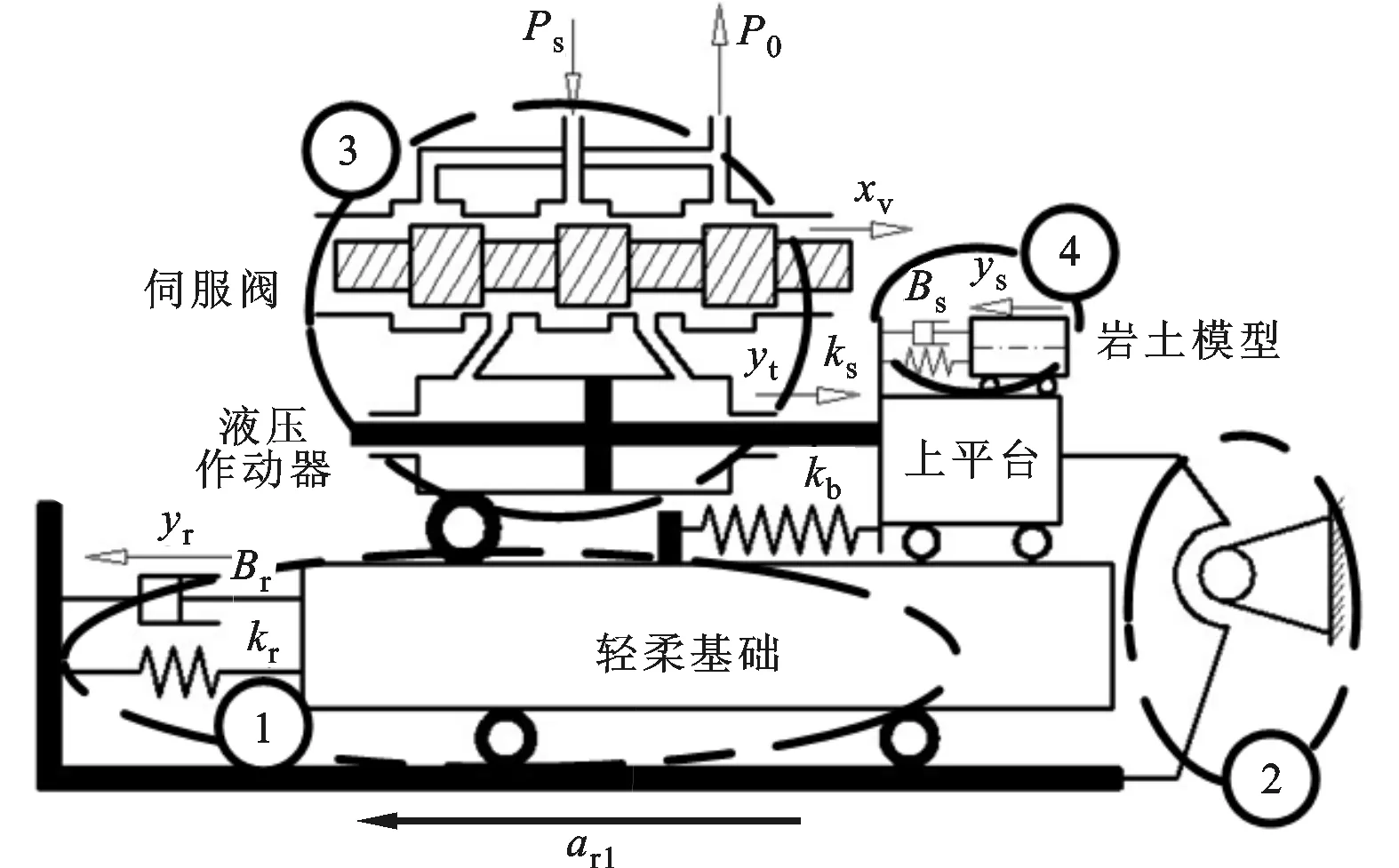
①:轻柔基础与上平台的动力学耦合;②:轻柔基础与上平台的运动学耦合;③:液压动力机构的动态特性;④:岩土模型的动态特性
Gyxv=
(1)
W″(s)=

W′(s)=
式中:kq表示伺服阀的流量增益;kce表示总的流量-压力系数;kb表示橡胶轴承的弹簧刚度;Ap表示液压缸的有效作用面积;ωs、ξs分别表示岩土模型的固有频率和阻尼比;ωr1、ξr1分别表示轻柔基础的综合固有频率和阻尼比;其他参数均由轻柔基础、液压动力机构、橡胶轴承综合确定。
2.2 离心振动复合环境对三级伺服阀的影响问题
目前,对三级伺服阀在离心力振动复合环境下的特性分析研究几乎处于空白,但关于两级伺服阀在离心力环境下的特性分析经验值得借鉴。贺云波等根据伯努利方程、流体冲量定理、力矩马达的力矩方程、喷嘴挡板的流量方程、挡板和二级阀芯的力平衡方程等,分析了伺服阀输入电流与阀芯位移间的关系[12]。与之相比,三级电液伺服阀在复合环境下的特性分析较上述研究要复杂得多,主要表现为:①三级伺服阀固定于轻柔基础上,而轻柔基础的运动又与2.1节中的耦合特性相关,因此垂臂安装时三级伺服阀除了在垂直于阀芯方向上受离心力的影响外,还在阀芯方向上受一个交变的振动载荷;②相比两级伺服阀,三级伺服阀加入了第三级功率级滑阀,结构的增加使三级伺服阀在复合环境下的特性分析变得更加复杂。鉴于以上两点,可推断从理论上研究该问题是较为困难的。因此,作者准备在振动台的后续调试试验中,实地测试三级电液伺服阀在极限复合环境下的响应,从而确定出伺服阀动态特性的摄动范围。
2.3 非线性因素对振动台性能的影响问题
非线性因素主要包括以下4类:①蓄能器的非线性;②岩土模型的非线性;③橡胶轴承的非线性;④动力机构的非线性。下面将逐一介绍上述因素。
2.3.1 蓄能器的非线性 由于液压滑环对传输流量的限制,单轴离心振动台很难通过地面油源实时供油,因此,振动台上的高压蓄能器被作为短时高频激振的油源,在激振过程中油液从高压蓄能器中持续流出,从而造成其出口压力的降低,即油源压力降低。从控制角度来讲,油源压力的降低将会造成流量增益的减小,从而降低系统的频宽和跟踪精度。
2.3.2 岩土模型的非线性 岩土模型的动态特性在整个激振过程中持续变化,进一步增加了系统的非线性。岩土模型动态特性的变化将会改变耦合传递函数的反谐振峰,也就改变了离心振动台位置闭环系统的主导零点,而在振动台的伺服控制策略中,一般会加入前馈控制器来对消系统频宽范围内的主导零极点,零极点位置的改变将会使前馈补偿失效,从而在一定程度上降低系统的性能。
2.3.3 橡胶轴承的非线性 目前作者已对单轴离心振动台的试验样机进行了一系列验证性试验,试验中暴露出橡胶轴承的非线性弹性变形将严重影响振动台对加速度波形的复现精度。除此之外,橡胶轴承的弹簧刚度既会影响耦合传递函数的开环增益,又会影响式(1)中惯性环节的转折频率ωb,因此橡胶轴承非线性对系统的跟踪精度和频宽都有较大影响。
2.3.4 动力机构的非线性 在线性耦合特性的推导过程中,同时对流量方程、流量连续性方程进行了线性化处理。在推导伺服阀的线性化流量方程时,选用的是负载流量QL、xv、负载压降PL均为0的工作点,此时伺服阀的流量增益最大,从稳定性角度考虑这是一种相对保守的线性化方法。在简化流量连续性方程时,假定活塞初始处于中间位置,此时执行机构的液压固有频率最低,系统特性最为保守。在实际情况下,由于PL、 活塞位置的变化范围都较大,需考虑液压动力机构非线性对系统性能的影响。
3 单轴离心振动台中的复合控制策略
3.1 复合控制策略概述
普通振动台的伺服控制策略包括前置滤波器、三状态控制器(包含三状态反馈和三状态前馈)、自由度控制器(包含自由度分解和自由度合成矩阵)、压力镇定控制器、速度合成控制器等,各部分的具体功能及设计方法在文献[4]中都有阐述。如图3所示,本文提出的复合控制策略是在传统伺服控制策略的基础上做了以下3方面补充:①引入几何解耦控制器,将上平台的绝对位移参考转化为上平台与轻柔基础间的相对位移参考,解决轻柔基础与上平台间的耦合问题;②引入鲁棒控制策略和两自由度控制策略,在保证系统稳定性的前提下提高系统性能;③引入负载干扰力补偿控制器,抑制负载动态特性变化对系统性能的影响。下面将详细叙述各补充部分的工作原理及设计过程。为简化设计过程,假设引入自由度控制和压力镇定控制器已基本解决了两套作动器间的内力耦合,因此在后续研究中将忽略作动器间的内力耦合,此时单轴离心振动台的动态特性可近似等效为单液压动力机构的动态特性。
3.2 几何解耦控制器
根据图2中的等效模型可推导出上平台、轻柔基础相对位移y到上平台绝对位移yt的传递函数,可表示为
(2)
图3 离心振动台的复合伺服控制策略
K=mr/(mt+ms+mr)
ωrb=((kr+kb)/mr)1/2
ξrb=(Br/2)(1/(mrkr+mrkb))1/2ωrts=
((mt+ms+mr)kr/mr)1/2
式中:mr、mt、ms分别代表轻柔基础、上平台、岩土模型的质量;kb、kr表示橡胶轴承和轻柔基础的弹簧刚度;Br表示轻柔基础的阻尼系数;ar、at表示在轻柔基础、上平台相应位置处的加速度。由式(2)可知,该耦合关系既与各部分质量有关,又受到橡胶轴承刚度、轻柔基础动态特性的影响。由于该单轴离心振动台已分别在轻柔基础、上平台上的对应位置安装了加速度传感器,因此可实时测量轻柔基础的加速度ar和上平台的加速度at。根据加速度传感器的测量结果和式(2)给出的传递函数形式,便可以辨识出该耦合关系的具体参数。最终,将Gyty的逆作为几何解耦控制器,用以将上平台的绝对运动参考转化成上平台、轻柔基础间的相对运动参考。
3.3 基于鲁棒控制的反馈控制器
如图4所示,作者借助系统方框图从以下6方面来说明各非线性因素对液压动力机构动态特性所产生的影响:①离心振动复合环境将会影响三级电液伺服阀的传递函数Gsv;②高压油从振动台中的高压蓄能器中持续流出造成油源压力的持续降低,油源压力降低将会减小伺服阀的流量增益kq;③在流量方程的线性化过程中,计算的流量增益kq是假设负载压降PL=0得到的,而实际过程PL的变化范围较大,这也会对伺服阀的流量增益kq产生影响;④在流量连续性方程的推导中,假设活塞的初始位置位于中间位置,此时的液压固有频率最小,而在实际情况下,初始位置不一定处于中位及油源压力的降低也会对压缩泄露流量到负载压降的传递函数GQPL产生影响;⑤橡胶轴承的非线性将会影响其弹簧刚度kb,其弹性曲线可通过预先的静力加载试验测量获得;⑥岩土模型动态特性的变化将会影响岩土模型自身的传递函数。
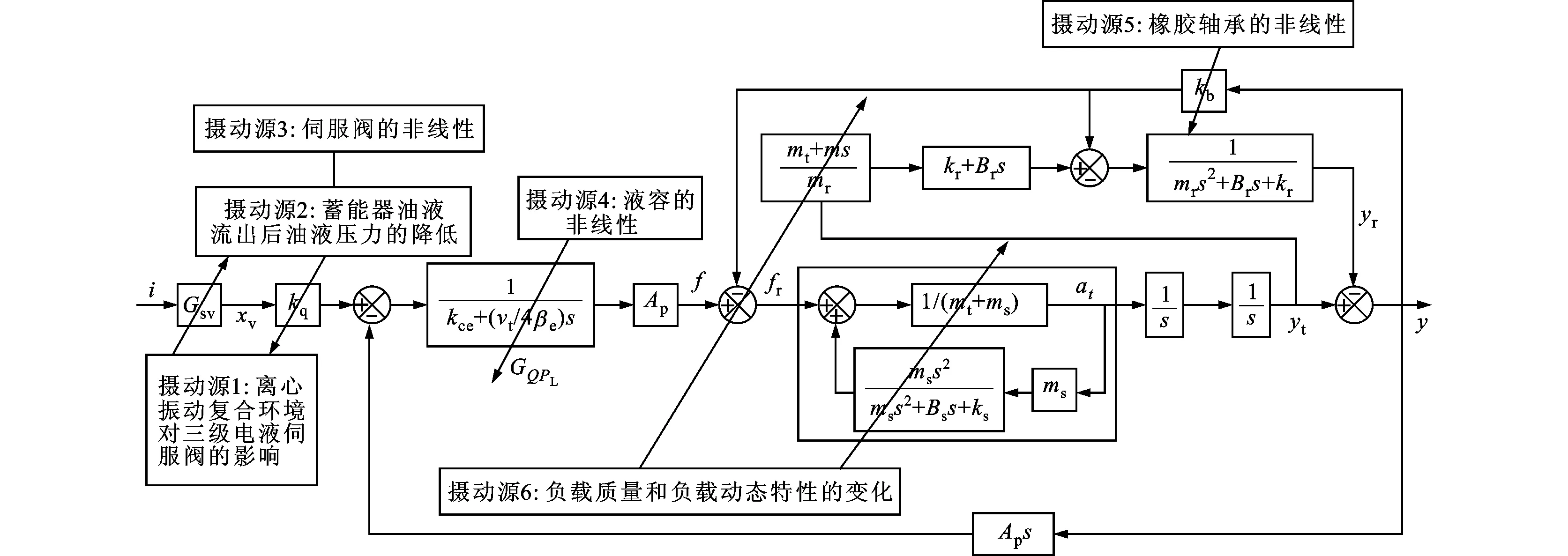
图4 离心振动台的传递函数框图及各摄动源对框图各部分的影响

3.4 基于两自由度控制策略的前馈控制器

①:液压缸出力到基础位移;②:液压缸出力到上平台位移;③:性能权重的等效表示

图6 两自由度控制策略的方框图
(3)

3.5 负载干扰力补偿控制器
如图7所示,负载干扰力Fd可表示为

(4)
式中:yr、yt、ys分别表示轻柔基础、上平台的绝对位移和岩土模型与上平台间的相对位移;kb(y)表示橡胶轴承的弹性曲线。液压作动器两腔都安装了压力传感器,上平台的绝对加速度、上平台与轻柔基础间的相对位移也都可由加速度、位移传感器测得,再结合预先测得的橡胶轴承的弹性曲线,在理论上可实时准确估计负载干扰力的值。本文将式(4)的功能定义为干扰力观测器。

图7 负载干扰力的定义
另外,在获得负载干扰力的估计值后,需根据估计的负载干扰力Fd计算添加到伺服阀上的补偿电流iD,本文将这部分命名为干扰力补偿器。根据负载干扰力Fd的定义修正图4中的方框图,结果如图8所示(用图8中标记为②的部分替换掉标记为①的部分)。参考图8,经简单推导,当补偿电流iD满足式(5)所示的关系式时,即
iD=Fd(kce+vt/4βes)/GsvkqAp
(5)
此时传感器位移输出y与Fd无关,说明伺服阀补偿电流iD在理论上完全消除了负载干扰力Fd对系统性能的影响。但是,考虑到系统的非线性,干扰力补偿器中的参数仅是针对系统的名义模型而设计的,因此在实际情况下补偿电流iD只能部分抵消负载干扰力Fd,并不能完全消除负载动态特性对系统性能的影响。为了确保摄动情况下负载干扰力补偿控制的稳定性,图中在干扰力补偿器前端加入比例增益klcd,调试时需将klcd从0逐步增加至1。

图8 负载力干扰力补偿控制器的原理图
4 仿真研究
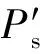
利用Matlab工具箱采用D-K迭代求解如图5所示的μ综合问题。经20次迭代,系统的结构奇异值逐步降至1以下,此时控制器Kμ的阶次为42阶。此后,采用基于Hankel奇异值的乘法误差模型对鲁棒控制器降阶,且将降阶后的鲁棒控制器转换成零极点模型形式,并剔除频宽范围以外的零极点,得到控制器的最终形式为
(6)

(a)流量增益kq与负载压降PL、油源瞬时应力间的关系

(b)压缩体积摄动下GQPL的相对误差E1、权重函数wv随频率的变化

(c)极限情况下Gfyt的相对误差E2、权重函数wfyt随频率的变化
(d)极限情况下Gfyr的相对误差E3、权重函数wfyr随频率的变化
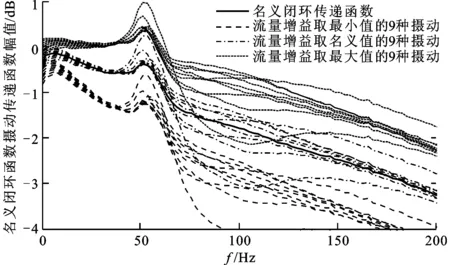
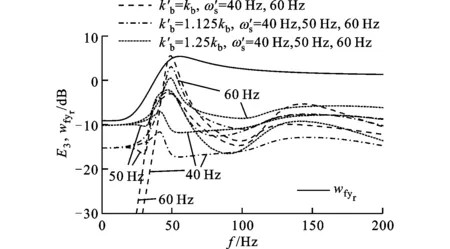
图10 名义闭环传递函数和27种摄动情况下传递函数的幅频特性
引入如图7所示的前馈补偿来进一步拓展系统频宽,文中选取的期望模型为
Gd=1/[(s/400π+1)(s2/(600π)2+1.4s/600π+1)]
(7)
经前馈补偿后,在控制系统中引入前置滤波器将加速度参考转换为位移参考,此时振动台上平台加速度at相对于加速度参考的频率响应如图11中虚线所示。比较采用和未采用两自由度控制算法的情况,如图11中虚线和点划线所示,可知前馈补偿控制已显著提高了系统的频宽,具体来说将系统频宽从21Hz提高到63 Hz。但是,这与伺服控制策略的预期频宽仍相距很大,造成此结果的主要原因在于轻柔基础在其固有频率(100Hz)附近对系统性能的限制。为此,在前置滤波器后端加入几何解耦控制器消除轻柔基础与上平台间的动态耦合,经解耦控制算法后,系统的频宽提高至250Hz左右,已完全满足系统的频宽要求,如图11中的实线所示。

图11 不同控制算法的比较
最后,通过仿真验证负载干扰力补偿控制器的作用。将岩土模型动态特性变化分为剧烈下降和随机波动两部分。文中采用的位移参考为50Hz的正弦信号,其频率恰为岩土模型的固有频率,此时负载力对系统特性的影响最为显著。当负载动态特性未发生变化时,位置闭环的响应信号如图12中P1段所示,可看出经负载干扰力补偿控制后,系统的相位滞后、幅值衰减仅有轻微改善。当岩土模型的固有频率和阻尼比突然下降至初始值的45%左右时,系统对正弦位移参考的响应如图12中P2段所示,可以看出采用负载干扰力补偿控制器的位置系统能更快地回到稳定状态,且在过渡过程的超调也减少至未采用补偿的50%左右。过渡完成之后,系统进入随机波动阶段。当岩土模型固有频率的变化范围为初始值的40%~80%、阻尼比变化范围为初始值的40%~80%时,系统的响应信号如图12中P3段所示。从P3段可知,采用负载干扰力补偿后系统的波形失真度也显著改善。综上所述,干扰力补偿控制器可有效抑制负载动态特性变化对系统性能的影响。
图12 负载特性摄动时,采用和未采用干扰力补偿器的系统对正弦位移参考的复现对比
5 结 论
本文引入几何解耦控制器,消除了轻柔基础与上平台间的动态耦合;引入负载干扰力补偿控制器,抑制了负载动态特性变化对系统性能的影响;最终,结合两自由度控制、鲁棒控制策略设计了系统的前馈、反馈控制器。仿真结果表明,该复合控制策略可有效提高单轴离心振动台系统在非线性、耦合特性影响下的性能。
[1] 张建民, 于玉贞, 濮家骝, 等. 电液伺服控制离心振动台系统研制 [J]. 岩土工程学报, 2004, 26(6): 843-845. ZHANG Jianmin, YU Yuzhen, PU Jialiu, et al. Development of a shaking table in electro-hydraulic servo-control centrifuge [J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 843-845.
[2] 王永志. 振动离心机系统工作原理与初步设计 [D]. 哈尔滨: 中国地震局工程力学研究所, 2010.
[3] CONTE J P, TROMBETTI T L. Linear dynamic modeling of a uni-axial servo-hydraulic shaking table system [J]. Earthquake Engineering and Structural Dynamics, 2000, 29: 1375-1404.
[4] 罗中宝, 杨志东, 丛大成, 等. 大型液压离心振动台的耦合特性分析 [J]. 振动与冲击, 2014, 33(11): 17-25. LUO Zhongbao, YANG Zhidong, CONG Dacheng, et al. The coupling characteristic analysis of large hydraulic centrifugal shaker [J]. Journal of Vibration and Shock, 2014, 33(11): 17-25.
[5] STOTEN D P, SHIMIZU N. The feedforward minimal control synthesis algorithm and its application to the control of shaking-tables [J]. Proceedings of the IMechE: Part I Journal of Systems and Control Engineering, 2007, 221: 423-444.
[6] GIZATULLIN A O, EDGE K A. Adaptive control for a multi-axis hydraulic test rig [J]. Proceedings of the IMechE: Part I Journal of Systems and Control Engineering, 2006, 221: 183-198.
[7] CUYPER J D, VERHAEGEN M, SWEVERS J. Off-line feed-forward and Hinf feedback control on a vibration rig [J]. Control Engineering Practice, 2003, 11: 129-140.
[8] VAES D, ENGELEN K, ANTHONIS J, et al. Multivariable feedback design to improve tracking performance on tractor vibration test rig [J]. Mechanical Systems and Signal Processing, 2007, 21: 1051-1075.
[9] UCHIYAMA Y, MUKAI M, FUJITA M. Robust control of electrodynamic shaker with 2DOF control using Hinf filter [J]. Journal of Sound and Vibration, 2009, 326: 75-87.
[10]IWASAKI M, ITO K, KAWAFUKU M, et al. Disturbance observer-based practical control of shaking tables with nonlinear specimen [C]∥Proceedings of the 16th IFAC World Congress International Federation of Automatic Control. Piscataway, NJ, USA: IEEE, 2005: 1251-1256.
[11]UCHIYAMA Y, FUJITA M. Robust disturbance-force compensator for time waveform replication of an electrodynamic shaker [J]. JSME Journal of System Design and Dynamics, 2010, 4(1): 1-12.
[12]HE Yunbo, CHUA P S, LIM G H. Performance analysis of a two-stage electrohydraulic servovalve in centrifugal force field [J]. Journal of Fluids Engineering, 2003, 125: 166-170.
(编辑 武红江)
ACombinedControlStrategyforLargeUniaxialCentrifugalShaker
LUO Zhongbao,YANG Zhidong,CHEN Liang,CONG Dacheng
(School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China)
A combined control strategy based on traditional servo control strategies is proposed to solve the dynamic coupling between the light-flexible base and the table, and to overcome the performance deterioration of centrifugal shaker caused by nonlinear factors. A geometry decoupling controller based on the equivalent coupling model is designed to eliminate the dynamic coupling between the light-flexible base and the table. Effects of all nonlinear factors on the system performance are taken into account, and a feedback controller based on robust control and a feed-forward controller based on 2-DOF control are presented to ensure the stability and control accuracy of the system. A load disturbing force compensator is also introduced to counteract the influence of load characteristics variation on system performance. Simulation results show that the bandwidth of the centrifugal shaker is improved to 250Hz after the feedback and feed-forward adjusting and geometry decoupling, and satisfies the anticipated bandwidth requirement of servo control strategy. When the load disturbing force is compensated, the overshoot and adjustment time of position close-loop in the radical drop section of load characteristics reduce to 50% of that without using compensation, and the close-loop waveform distortion in the random fluctuation section of load characteristics is also improved.
centrifugal shaker; geometry decoupling controller; robust control; 2-DOF control strategy
2014-03-10。
罗中宝(1986—),男,博士生;丛大成(通信作者),男,教授,博士生导师。
国家自然科学基金资助项目(51205077)。
10.7652/xjtuxb201412021
TU352.1
:A
:0253-987X(2014)12-0131-09

