转台轴承静刚度建模及其影响因素分析
位文明,吕盾,张俊,赵万华
(西安交通大学机械制造系统工程国家重点实验室, 710054, 西安)
转台轴承静刚度建模及其影响因素分析
位文明,吕盾,张俊,赵万华
(西安交通大学机械制造系统工程国家重点实验室, 710054, 西安)
为了改善转台的动静特性,分析了三排圆柱滚子转台轴承静刚度与轴承结构型式、装配工艺和外载荷的关系。结合轴承游隙、螺钉拧紧力矩、径向与轴向滚子间的相互作用和外载荷等因素,将轴向滚子与轴圈间的接触看作理想平面接触,考虑径向滚子压力沿轴向的分布,并利用Boussinesq力与变形关系式求解实际的压力值,通过求解轴承的整体静力平衡方程,得到了三排圆柱滚子转台轴承5个方向的静刚度值。分析结果表明:转台固有频率测试与理论值误差不超过3.0%,验证了刚度理论模型的准确性;轴向滚子与径向滚子载荷间的相互作用很小;螺钉拧紧力矩、径向游隙和外载荷对转台轴承刚度有重要影响,随着螺钉拧紧力矩和径向预压量的增大,外载荷对刚度的影响减弱。
三排圆柱滚子轴承;静刚度;预紧力;转台
转台在使用过程中要受到切削力、工件和夹具重力的作用。转台支承系统的刚度不仅影响台面的静力变形,同时还决定了工件-夹具-转台系统的动刚度,进而影响切削稳定性和零件的加工精度。转台的转动部分(转轴、蜗轮和刹紧装置等)通过转台轴承与基座相连,转台轴承的静刚度直接影响台面的几何精度和动态特性。转台轴承能够同时承受轴向、径向载荷和倾覆力矩的作用,它的使用大大简化了数控转台的机械结构。
常用的转台轴承有单排四点接触球轴承、双排球轴承、交叉圆柱滚子轴承和三排圆柱滚子组合轴承等4种形式。关于单排径向圆柱滚子轴承刚度的研究表明:圆柱滚子轴承的刚度不仅受到结构形式和安装工艺的影响,还与转速、润滑状态和外载荷等实际工况密切相关[1-4]。目前,三排圆柱滚子轴承的研究主要集中在计算滚子载荷和应力分析,以研究轴承的寿命问题[5-8],分析时最重要的是得到滚子的实际受力状态。文献[5-6]利用Hertz理论描述圆柱滚子与轴圈的接触,通过求解静力平衡方程得到各个滚子的实际载荷。文献[7]为了考虑轴圈和螺钉的柔性,建立了三排圆柱滚子轴承的有限元模型,圆柱滚子及其与轴圈的接触特性等效为梁单元以简化计算,通过有限元分析得到滚子的实际受力状态。上述分析只能得到作用于滚子的整体载荷大小,而圆柱滚子受载时其压力分布沿轴向变化明显。为此,文献[8]利用切片模型来描述圆柱滚子的接触状态以得到压力沿其轴向的分布状态。但是,关于三排圆柱滚子转台轴承静刚度的研究还很少。为了准确地分析转台台面的静力变形和动态特性,有必要分析转台轴承的静刚度及其随载荷的变化规律。
本文考虑径向圆柱滚子沿长度方向的载荷分布及其与轴向滚子载荷的相互作用,建立了三排圆柱滚子转台轴承的静刚度矩阵的计算方法,并通过转台的固有频率测试对刚度的理论值进行验证,进一步分析了静刚度随径向游隙、螺钉拧紧力矩和外载荷的变化规律。
1 刚度矩阵的计算方法
三排圆柱滚子转台轴承由L型轴圈、推力垫圈、座圈、两排轴向圆柱滚子和一排径向圆柱滚子组成,如图1所示。分析时作如下假设:轴承受到倾覆力矩和轴向力作用;内外圈均为刚性,不发生变形;所有的变形均发生在圆柱滚子上及其与轴圈和座圈的接触区域;径向载荷和倾覆作用在同一个平面上;座圈静止,轴圈在外载荷作用下发生相对位移;由于转台轴承转速不高,不考虑离心力的作用。
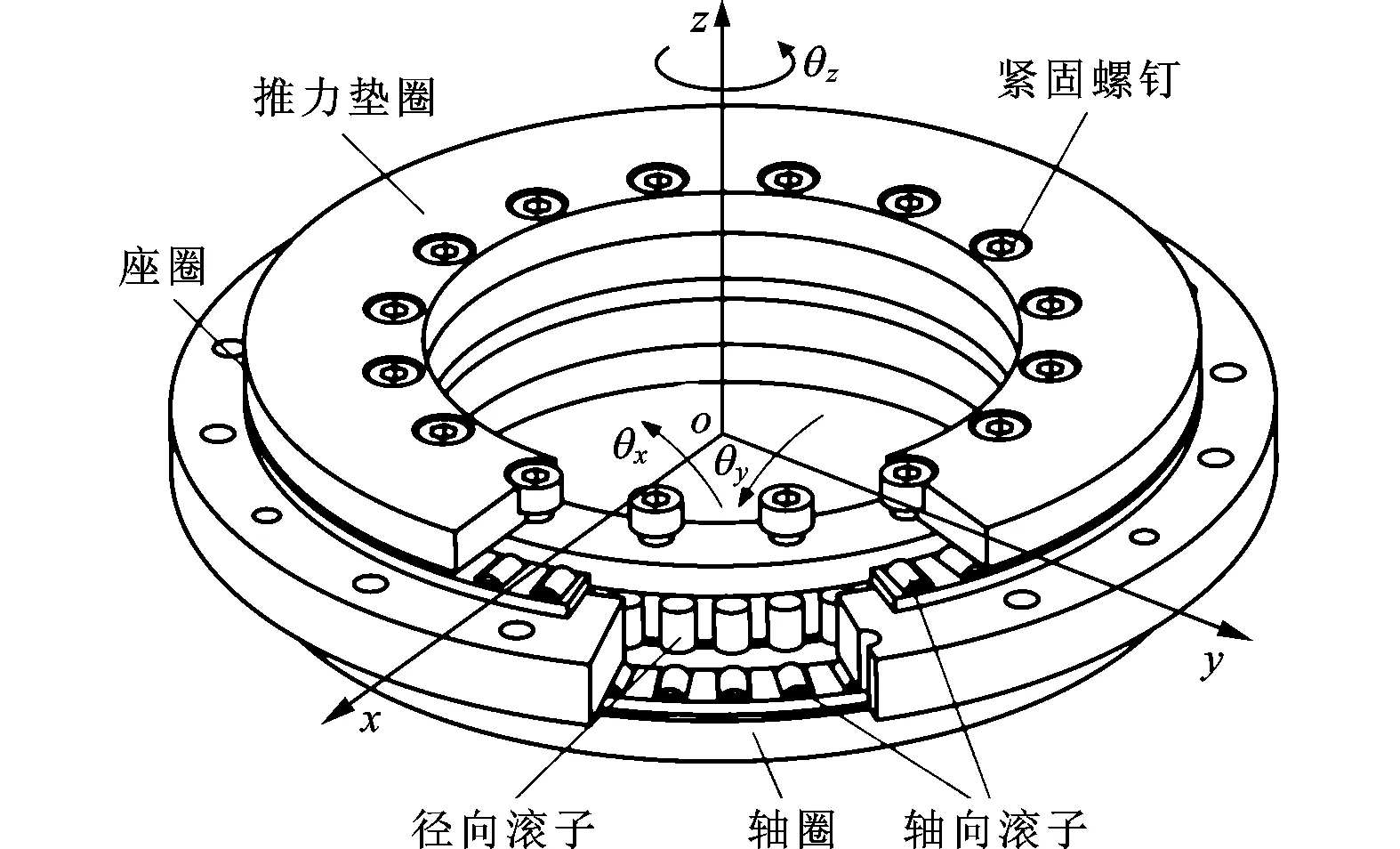
图1 三排圆柱滚子转台轴承结构示意图
1.1 轴向部分滚子的受力分析
轴向部分滚子的受力状态如图2所示,轴向的两排滚子中第i个滚子与x轴夹角
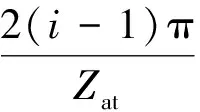
(1)
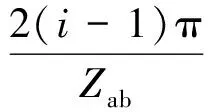
(2)
式中:φat0、φab0分别为上排、下排第一个滚子与x轴间的夹角;Zat、Zab分别为上排、下排滚子数量,一般有Zat=Zab。

图2 轴向部分滚子受力示意图
那么,上排第i个滚子与轴圈间的相对转角为
θati=-θxsinφati+θycosφati
(3)
上排第i个滚子的总压缩量为
δati=ra(-θxsinφai+θycosφai)+
0.5La|θati|+δz-0.5ua
(4)
式中:ra为轴向滚子中心所在圆的半径;La为轴向滚子长度;δz为轴圈沿z向位移;ua为轴向游隙,正值为间隙,负值为预压量。
同理,下排第i个滚子处滚子与轴圈间的相对转角为
θabi=θxsinφabi-θycosφabi
(5)
下排第i个滚子的总压缩量为
δabi=rab(θxsinφabi-θycosφabi)+
0.5La|θabi|-δz-0.5ua
(6)
由于转台轴承的径向尺寸远大于圆柱滚子的长度,可以不考虑轴向滚子上载荷分布对刚度的影响,利用理想平面接触来描述轴向滚子的接触变形与受力间的关系[9]。不考虑离心力时,轴向滚子与内外圈之间的接触变形和夹角相等。同时,为了保证滚子接触,在任何位置满足0.5Laθai+δai>0,并且有

(7)
式中:θin_ai、θex_ai分别为轴向滚子与轴圈、座圈间的夹角;θai、δai分别为轴向滚子与轴圈间的夹角和压缩量。
那么,轴向部分滚子上的力和力矩分别为
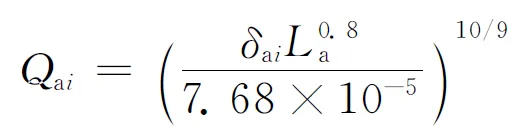
(8)

(9)
1.2 径向部分滚子的受力分析
径向部分滚子在Fx、Fy和My作用下的受力状态如图3所示,第i个滚子与x轴夹角
φri=φr0+2(i-1)π/Zr
(10)
式中:φr0为径向第一个滚子与x轴间的夹角;Zr为径向滚子个数。
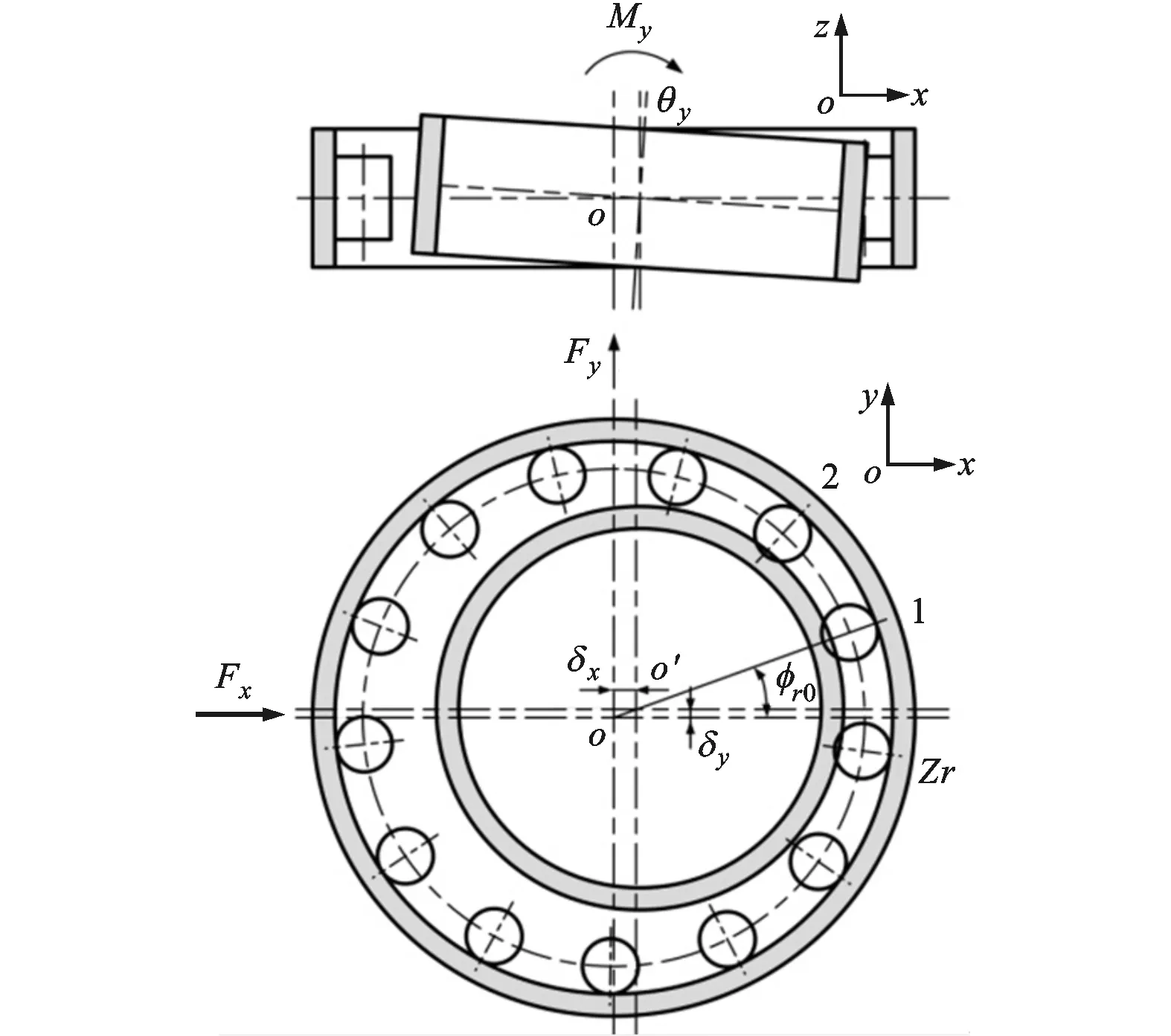
图3 径向部分滚子受力示意图
径向圆柱滚子的初始游隙大小为
uri=0.5ur(1-cos(φri-φur))
(11)
式中:ur为径向游隙,正值为间隙,负值为预压量;φur为Fx、Fy合力与x轴的夹角。
那么,第i个滚子的总压缩量为
δri=δxcosφri+δysinφri+0.5Lr|θri|-
0.5ur(1-cos(φri-φur))
(12)
式中:δx、δy分别为轴圈沿x、y向的径向位移;Lr为径向滚子长度。
当轴圈的角位移分别为θx、θy(方向依据右手定则)时,径向第i个滚子与轴圈间的相对转角为
θri=θxsinφri-θycosφri
(13)
在不考虑离心力时,滚子与座圈和轴圈间的接触变形相等,滚子与座圈和轴圈间的夹角也相等。为了保证滚子接触,在任何位置满足0.5Lθri+δri>0,那么有
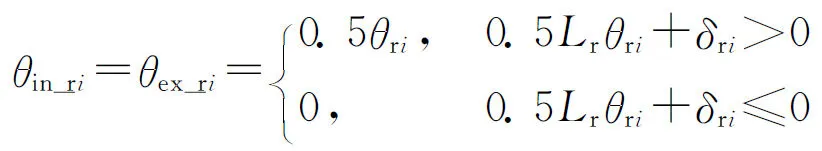
(14)
考虑压力沿圆柱滚子长度方向分布时,可以依照Boussinesq的集中力与变形的关系求解接触力[10]。假设第i个圆柱滚子与轴圈间的接触区域为矩形,建立原点在接触区中心处的局部坐标系o(xi,yi,zi),yi轴沿滚子轴向,zi轴沿滚子径向。将滚子与轴圈的矩形接触区域等分为Ni(NxNy)个单元,每个单元上的压力pij(j=1,…,Ni)均匀分布时,有
(15)
式中:系数k0如式(16)所示;zik为第k个单元的几何中心处的滚子轮廓值,如式(17)所示;Gikj为影响系数,表示作用在单元j上单位压力引起的单元k中心处的变形,如式(18)所示;δi为滚子与轴圈间的相对位移。

(16)
式中:E1、E2分别为滚子、轴圈材料的弹性模量;ν1、ν2分别为滚子、轴圈材料的泊松比。
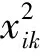
(17)
式中:(xik,yik)(-R≤xik≤R,-L/2≤yik≤L/2)为第k个单元的中心坐标;R为径向滚子半径;L为径向滚子长度;θi为滚子与轴圈间的相对转角。
Gikj=G(u+ai,v+bi)+G(u-ai,v-bi)-
G(u-ai,v+bi)-G(u+ai,v-bi)
(18)
式中:u=|xik-xij|,v=|yik-yij|;ai、bi分别为矩形单元的半宽和半长;G为积分求得的函数,有
G(x,y)=xln(y+(x2+y2)1/2)+
yln(x+(x2+y2)1/2)
(19)
在圆柱滚子的整个接触区域上,有
k0Gpi=δiI-zi
(20)
式中:I为Ni×1的单位向量;zi为Ni×1的向量。
接触面上的合力与外力相平衡,那么有
(21)
同时,发生接触网格上的压力应满足
pij≥0,j=1,…,Ni
(22)
利用式(20)~式(22),通过迭代求解,可以得到滚子与轴圈的实际接触区域和接触压力pij。那么,径向滚子上的合力和合力矩分别为
(23)
(24)
式中:ari、bri分别为第i个滚子接触区域离散网格单元的半宽和半长;Nri为滚子与轴圈的矩形接触区域等分单元数;prij(j=1,…,Nri)为单元上均匀分布的压力;yrij为单元几何中心y的坐标。
1.3 轴向滚子的初始游隙
轴向滚子的初始游隙由紧固螺钉预紧力决定,给定螺钉拧紧力矩下轴向滚子的初始游隙为
(25)
式中:Zb为螺钉的个数;T为拧紧力矩;db为螺钉直径;Kb为螺钉力矩系数,一般取值0.2。由于螺钉的预紧作用,轴向滚子的初始游隙都为负值。
1.4 转台轴承的静刚度求解
综合径向和轴向滚子的受力状态分析,可以得到三排圆柱滚子转台轴承的整体静力平衡方程为

(26)
求解时,首先根据螺钉的预紧力矩T和式(25)求出轴向滚子的初始游隙,然后根据径向接触区域的网格参数和外载荷大小,利用Newton-Raphson方法求解式(26),得到给定载荷下轴承内圈的位移量q={δx,δy,δz,θx,θy}T和各个径向圆柱滚子的载荷分布。
对式(26)求导,可以得到如下转台轴承整体静刚度矩阵

(27)
2 理论模型的实验验证
选择图4所示的转台作为研究对象,转动体通过YRT325型三排圆柱滚子转台轴承与基座相连,轴承的结构参数如表1所示。轴承轴圈、推力垫圈、座圈和滚子的材料均为轴承钢,其密度为7.85×103kg/m3,弹性模量为2.06×1011Pa,泊松比为0.3。转台转动体的质量为175.1kg,在坐标系o(x,y,z)中绕x、y、z轴的转动惯量分别为3.9、3.9和5.5 kg·m2。采用LMS Test Lab振动测试系统对转动体的动特性进行测试,实验中采用单点激励、多点拾振的测试方法,12个加速度传感器测点均匀布置在转动体的上表面,如图4所示。

表1 YRT325转台轴承的结构参数

图4 转台动特性测试装置示意图
根据图5所示的转动体的等效动力学模型和转台轴承的支承刚度,可以得到转动体的固有频率。从表2可以看到,转动体3个方向固有频率的理论值与实验值很接近,验证了本文转台轴承刚度计算模型的准确性。实验中转台轴承主要受到转动体z向重力作用,由于转动体和转台轴承结构的对称性,其x、y向固有频率,及绕x轴、绕y轴固有频率的值分别相同。因此,只比较了x向、z向和绕x轴对应的3阶固有频率。紧固螺钉的实际预紧力与理论值的差异使得实际轴向刚度和转动刚度与理论值不同,进而使得固有频率的理论值与实验值存在差别。

图5 转动体的等效动力学模型

表2 转动体固有频率的理论值与实验值对比
3 刚度的影响因素分析
3.1 游隙的影响
由式(25)得到不同拧紧力矩下轴向滚子的实际游隙ua,如图6所示,可以看到轴向游隙ua随着拧紧力矩的增加显著增大。

图6 轴向游隙ua随螺钉拧紧力矩T的变化规律

图7 kzz随轴向和径向游隙的变化规律

图8 kθx随轴向和径向游隙的变化规律

图9 kxx随径向游隙的变化规律
转台轴承的径向和轴向游隙对z向平动刚度kzz和绕x轴的转动刚度kθx的影响如图7和图8所示。从图中可以看出,当螺钉预紧力增加使得轴向游隙ua增大时,kzz和kθx都随之显著变大,但是,kzz和kθx基本不随径向游隙ur变化。从图9中可以看到,径向游隙ur对径向支承刚度kxx影响显著,但是当ur进一步增加到-6.0μm后,径向支承刚度基本不发生变化。这是由于轴向和径向滚子数量众多,L型轴圈的转角变形很小,L型轴圈的转动不会使得径向滚子上载荷及其沿长度方向的分布产生很大的波动,同时滚子长度为12 mm,远小于轴向滚子中心圆直径,使得径向滚子产生的反力矩相对较小,对轴向滚子的载荷分布和刚度的贡献很小。综上分析可知,轴向支承刚度kzz和转动刚度kθx主要由轴向游隙ua决定,径向支承刚度主要由径向游隙ur决定,径向滚子对转台轴承的轴向刚度和转动刚度影响很小。
3.2 外载荷的影响
在不同螺钉拧紧力矩下,转台轴承轴向刚度kzz和转动刚度kθx随外载荷的变化规律如图10和图11所示。当预紧力矩为5.0N·m时,kzz和kθx都随着Fz的增加而显著减小,这是由于外载荷的作用使得轴向上排滚子与推力垫圈间的接触力变小,甚至发生脱离,而扭矩Mx的增加对kzz和kθx的影响很小。从图12和图13可以看到,kzz和kθx随着拧紧力矩的增加而增大,当拧紧力矩增加到20.0N·m时,Fz的增加基本不改变kzz和kθx的值。

图10 kzz随载荷Fz和Mx的变化规律(T=5.0N·m)

图11 kθx随载荷Fz和Mx的变化规律(T=5.0N·m)
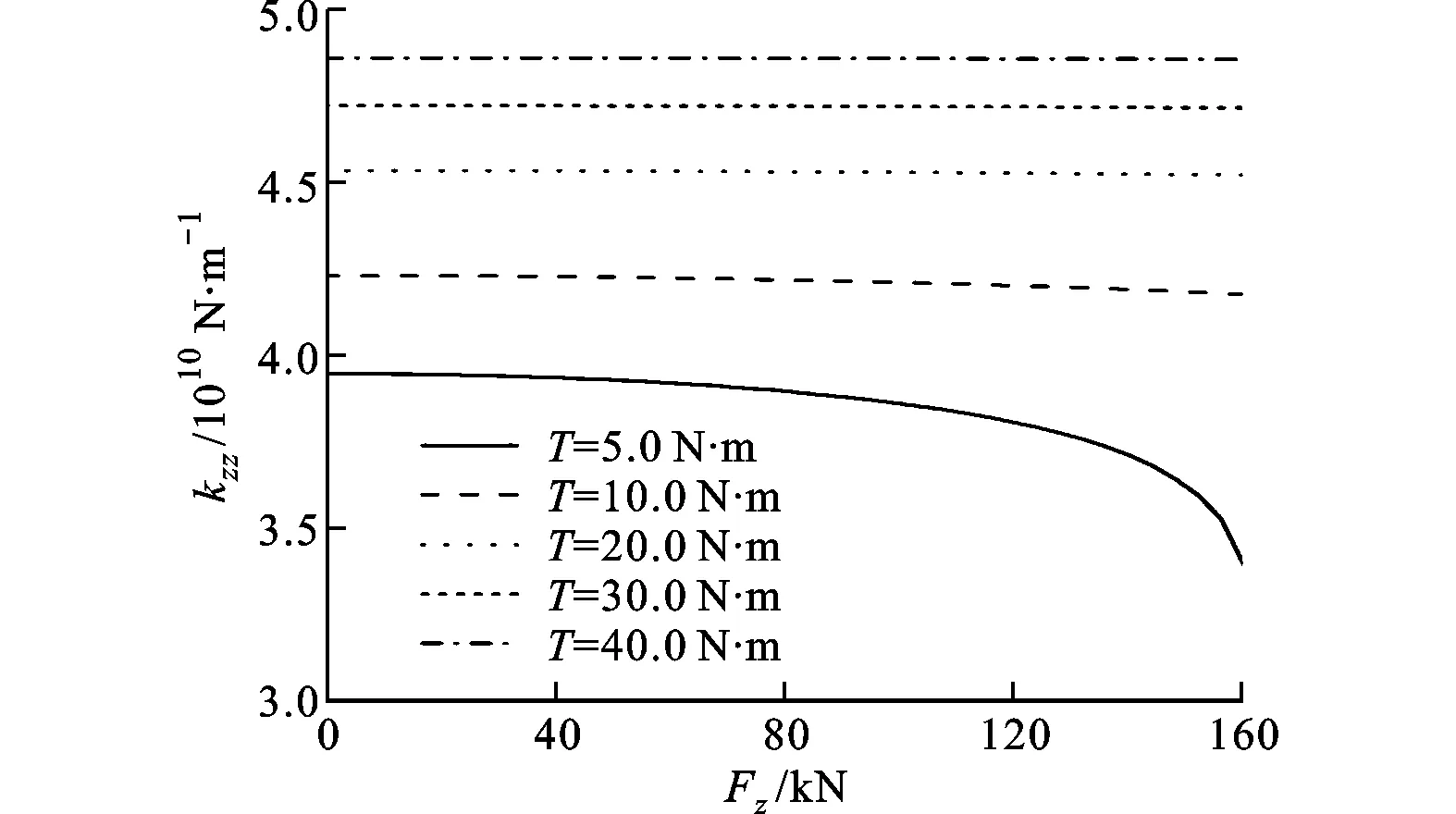
图12 kzz随载荷Fz和T的变化规律

图13 kθx随载荷Fz和T的变化规律

(a)kxx
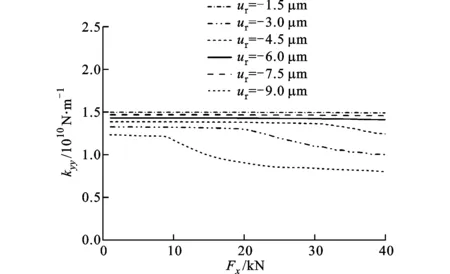
(b)kyy
在不同径向游隙ur下,径向支承刚度kxx随外载荷的变化规律如图14所示。当预压量小于6.0μm时,kxx和kyy在Fx增大到某一值时急剧减小,这是由于L型轴圈随着Fx移动,在Fx相反方向的部分径向滚子与轴圈间脱离接触,而当预压量超过6.0μm后,Fx对kxx和kyy基本没有影响。与kxx不同的是,kyy出现突变的外载荷较大,这是由于Fx作用时对x向滚子的实际接触状态影响更显著。同时,随着径向预压量的增加,不同载荷时的kxx和kyy整体上逐渐增加。当预压量大于6.0μm时,kxx和kyy随着预压量增加的趋势变缓。预压量由6.0μm增加到7.5 μm时,不同载荷下kxx和kyy的最大增加幅度为6.3%,而预压量由7.5 μm增加到9.0μm时,刚度的最大增加幅度减小到3.1%,此时预压量对kxx和kyy影响很小。
4 结 论
(1)本文结合游隙、径向滚子与轴向滚子间的相互作用和外载荷等因素,给出了计算三排圆柱滚子转台轴承5个方向静刚度的方法,并通过转台固有频率的理论值和实验结果的对比,验证了该方法的准确性。
(2)径向滚子的压力分布对轴向滚子的载荷影响很小,基本不改变转台轴承轴向刚度和转动刚度。
(3)当螺钉拧紧力矩较小时,kzz和kθx随着Fz的增加而显著减小。kzz和kθx随着拧紧力矩的增加而增大,当拧紧力矩增加到20.0N·m后,kzz和kθx基本不随Fz改变,而Mx对kzz和kθx基本没有影响。
(4)当径向预压量小于6.0μm时,径向刚度在外载荷作用下发生突变,发生突变的径向载荷随着预压量的增加而增大。这种现象随着径向预压量的增加而逐渐消失。
本文的分析可以为转台轴承的选型和装配工艺规划提供依据。
[1] LIM T C, SINGH R. Vibration transmission through rolling element bearings: part I bearing stiffness formulation [J]. Journal of Sound and Vibration, 1990, 139(2): 179-199.
[2] GUO Y, PARKER R G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model [J]. Mechanism and Machine Theory, 2012, 51: 32-45.
[3] 邹英永, 温建民, 于广滨. 径向力和弯矩联合作用下滚子轴承的刚度计算 [J]. 中国机械工程, 2006, 17(15): 1572-1575. ZOU Yingyong, WEN Jianmin, YU Guangbin. Stiffness calculation of roller bearings with radial force and moment loads [J]. China Mechanical Engineering, 2006, 17(15): 1572-1575.
[4] 崔立, 王黎钦, 郑德志, 等. 航空发动机高速滚子轴承动态特性分析 [J]. 航空学报, 2008, 29(2): 492-498. CUI Li, WANG Liqin, ZHENG Dezhi, et al. Analysis on dynamic characteristics of aero-engine high-speed roller bearings [J]. Acta Aeronautica Et Astronautica Sinica, 2008, 29(2): 492-498.
[5] 于春来, 刘洪海, 郭云飞. 三排圆柱滚子转盘轴承寿命计算 [J]. 轴承, 2011(8): 7-8. YU Chunlai, LIU Honghai, GUO Yunfei. Life of three row cylindrical roller slewing bearings [J]. Bearings, 2011(8): 7-8.
[6] AGUIRREBEITIA J, ABASOLO M, AVILÉS R, et al. Theoretical calculation of general static load-carrying capacity for the design and selection of three row roller slewing bearings [J]. Mechanism and Machine Theory, 2012, 48: 52-61.
[7] KANIA L, KRYNKE M, MAZANEK E. A catalogue capacity of slewing bearings [J]. Mechanism and Machine Theory, 2012, 58: 29-45.
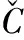
[9] HARRIS T A, KOTZALAS M N. Rolling bearing analysis: advanced concepts of bearing technology [M]. Boca Raton, FL, SUA: CRC Press, 2006: 17-27.
[10]符晶, 王慧, 温诗铸. 任意弹性表面接触问题的数值解法及对滚子修缘的分析 [J]. 轴承, 1990(1): 6-12. FU Jing, WANG Hui, WEN Shizhu. Numerical method for contact problem between arbitrary elastic surfaces and analysis of crowned roller [J]. Bearings, 1990(1): 6-12.
(编辑 杜秀杰)
StaticStiffnessofThree-RowCylindricalRollerBearingforRotaryTable
WEI Wenming,LÜ Dun,ZHANG Jun,ZHAO Wanhua
(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710054, China)
To improve static and dynamic performances of rotary table, the effects of configurations, assembling technology and external load on the static stiffness of a three-row cylindrical roller bearing for rotary table are investigated. A theoretical model of static stiffness of three-row cylindrical bearing for rotary table is proposed considering the clearance, bolt preloads, and reactions of axial and radial rollers with external load. The contacts between the axial rollers and the outer ring are treated as ideal plane contact. And the actual contact forces and their distribution along the axial of radial rollers are obtained by Boussinesq’s relationship between force and deformation, the static stiffness in five directions is then sought out by solving the static equivalent equations. It is shown that the maximum error between experimental and theoretical results of natural frequency of the rotary table is less than 3.0%, thus the theoretical model is verified. The reactions between loads acting on the axial rollers and radial rollers are negligible. The bolt preloads, radial clearance and external load exert obvious effects on the static stiffness of rotary table bearing, and the effect of external load decreases with the increasing preloads of bolts and radial clearance.
three-row cylindrical roller bearing; static stiffness; preload; rotary table
2014-06-19。
位文明(1985—),男,博士生;赵万华(通信作者),男,教授,博士生导师。
国家自然科学基金重点资助项目(51235009);国家科技重大专项资助项目(2011zx04016-031)。
时间:2014-10-23
10.7652/xjtuxb201412002
TH133.33
:A
:0253-987X(2014)12-0008-07
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141023.1634.006.html

