孤岛微电网中逆变器并联功率与电压均衡控制技术研究
耿志清,卓放,宁改娣,师洪涛,张东,翟灏
(西安交通大学电气工程学院, 710049, 西安)
孤岛微电网中逆变器并联功率与电压均衡控制技术研究
耿志清,卓放,宁改娣,师洪涛,张东,翟灏
(西安交通大学电气工程学院, 710049, 西安)
针对微电网中采用传统双环控制的逆变器并联系统功率均分精度较低以及输出电压和频率的偏移问题,分析了并联系统的功率均分机理及输出电压外特性,提出了一种基于虚拟阻抗和输出电压-频率瞬时值调节的逆变器并联运行功率与电压均衡控制策略。在传统的双环控制器中增加虚拟阻抗环,改善了输出阻抗特性,采用P-ω、Q-V下垂控制法提高了功率均分精度;同时加入输出电压幅值和频率调节环,对由下垂引起的电压、频率的偏移进行二次调节,能保证较高的输出电压质量。仿真和实验结果表明,所提出的功率与电压均衡控制策略使孤岛微网中的并联逆变器较好地均分负载功率,同时维持输出电压和频率为额定值,验证了所提算法的有效性。
微电网;逆变器并联;功率均分;电压-频率调节;均衡控制
随着世界传统能源逐渐枯竭,能源危机日渐严重,以新能源为支撑的微电网以其独特的优势应运而生。单台逆变电源由于受到容量和可靠性的限制,难以满足负载的功率需求,为了提高逆变电源容量和可靠性,微网中多采用逆变器并联技术[1-7]。为了获得精确的功率均分精度和保持微网电压和频率的稳定[5],在各分布式发电单元间设置通讯互联线以及中央控制器,可实现对逆变器输出电压的控制。但是联络线的加入增加了成本,限制了分布式系统的距离,还会降低系统的稳定性[8-10]。无联络线控制技术仅需测量分布式系统的本地信号,无需通讯就能实现对电压的控制,因而得到了广泛应用[2,6-8]。
在无联络线的逆变器并联系统中,引入电力系统中同步发电机的自下垂特性,即以各并联逆变器输出的有功功率和无功功率为控制变量,调整各逆变器输出电压的幅值和频率,从而使得各并联逆变器输出电压得以同步,最终实现消除环流均分负载的目的[8-9]。传统的下垂控制没有考虑电压和频率的恢复问题,也就是类似于传统发电机中的二次调整问题,微电网中功率波动越大,电压和频率的瞬时偏差越大。基于此,有学者提出根据功率变化实时调节下垂系数,即在功率波动较大时采用较小的下垂系数来减小电压和频率的偏移[10]。但是,下垂系数过小会影响系统动态响应、过大则会引起系统不稳定,其取值需进行折中考虑[6]。微电网由于容量较低,一般接入到低压配电网中[2,10-11],而低压线路的线路电阻远大于电抗(阻抗比可达7.33)[12],当输出阻抗及线路阻抗之和为阻性时,P-Q解耦将受到影响,且在稳态时无功功率均分效果较差。因此,逆变器的输出阻抗特性影响着下垂控制的效果。
文献[10]提出通过改变控制参数来增大输出阻抗以减小无功环流,同时根据功率波动大小实时改变下垂系数,以减小功率波动引起的电压、频率与额定值的偏差过大。但使用该方法时,电压、频率偏离额定值的情况仍存在。利用虚拟阻抗来改变输出阻抗特性,并减小线路阻抗差异对功率均分的影响得到广泛应用[1,3,6,8]。文献[11]提出在低压微电网中加入感性虚拟阻抗来减小输出电阻对系统环流的影响,同时通过对传统下垂控制进行改进,有效降低了线路电阻对并联均流的影响。但是,该方法以输出滤波电容很小为前提,当逆变器容量较大且对滤波要求较高而采用较大电容时,均流效果受到影响。采用下垂控制的逆变器在功率分配精度与电压质量之间存在矛盾,现有的分层控制技术虽然可以在一定程度上减小电压、频率与额定值的偏差,但由于各分布式电源与中央控制器之间需要通信,降低了系统的可靠性[13]。
本文综合考虑了并联系统的功率均分机理及输出电压的外特性,在传统的双环并联控制器中增加虚拟阻抗环,改善了输出阻抗特性,采用P-ω、Q-V下垂控制法提高了功率均分精度。同时,加入输出电压幅值和频率调节环,对由下垂引起的电压、频率的偏移进行二次调节,能保证较高的输出电压质量,实现功率与电压的均衡控制。通过仿真和实验验证了该算法的有效性。
1 微电网中逆变器并联控制策略
1.1 传统逆变器并联控制技术
本文以两台逆变器并联等效模型(见图1)为研究对象,对逆变器并联时的功率均分问题进行分析。
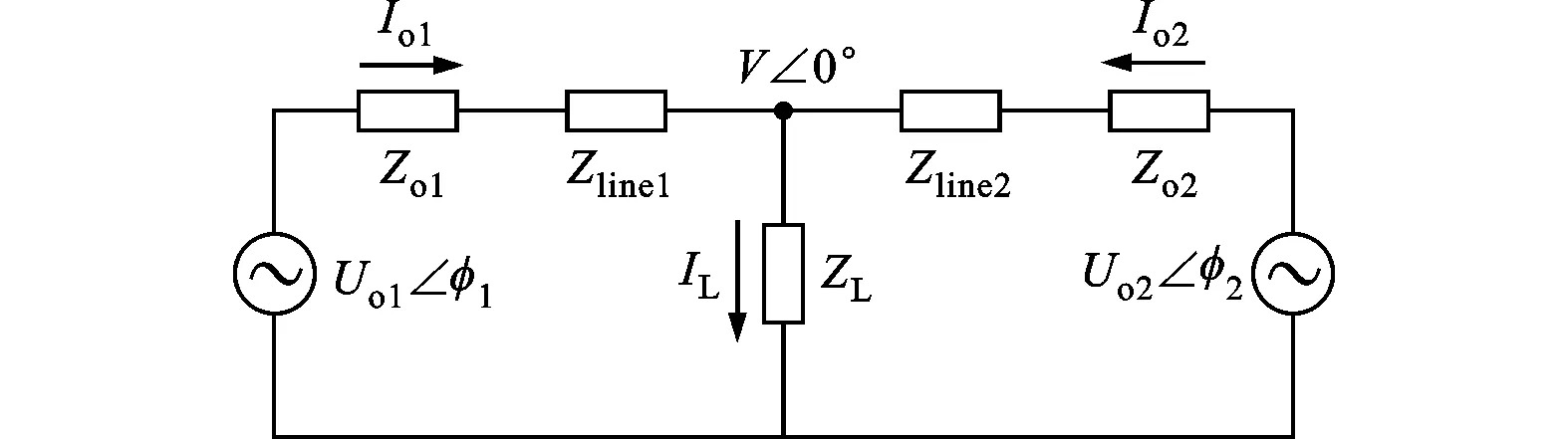
图1 两台逆变器并联等效模型
在上述模型中,定义两台逆变器的输出电压为Uoi∠φi(i=1,2),φi为输出电压与母线电压的相角差;输出电流为Ioi,逆变器输出阻抗与线路阻抗和为Zi∠θi=Zoi+Zlinei=Ri+jXi,Zi和θi分别为其幅值和相角;负载阻抗为ZL,负载电流为IL。假设公共交流母线电压V=V∠0°作为参考向量,由于Uoi的相角是通过锁相环对母线电压V锁相得到的,因而Uoi和V的相角差很小(sinφi≈φi,cosφi≈1);当逆变器输出阻抗与线路阻抗之和为感性时,Zi=jXi(θi=90°),逆变器的输出有功、无功功率为[5-6]

(1)

(2)
分析式(1)、式(2)可见,有功功率Pi主要由φi决定,而无功功率Qi主要由Uoi和V的幅值差决定,因此在一定程度上,有功、无功功率可通过控制频率和电压来实现独立控制,由此可得传统的P-ω、Q-V下垂控制方程

(3)
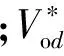
当逆变器输出阻抗与线路阻抗之和为阻性时,Zi=Ri,此时θi=0°,下垂控制变为P-V、Q-ω,下垂控制方程如下

(4)
当逆变器输出阻抗与线路阻抗之和为阻感性时,且有0°<θi<90°,此时下垂控制方程为

(5)
通常,不同电压等级的线路具有不同的阻抗比(R/X)[10],因此应综合考虑逆变器输出阻抗及线路参数特性,选取合适的下垂控制策略。
1.2 逆变器并联的功率均分机理
微电网中多个并联的逆变电源通过共同的交流母线作为其输出的唯一连接,并联逆变电源之间需要根据自身的输出功率,通过合理、优化的控制方法调节各自的输出电压幅值、频率和相位,从而实现各逆变单元之间负载功率的合理分配。由式(1)、式(2)可知,逆变电源的输出功率与其输出阻抗、线路阻抗及输出电压的幅值和相角差有关,当各并联逆变器的输出阻抗与线路阻抗都相等时,P-ω、Q-V下垂控制可实现各逆变器的功率均分。但在实际情况下,各逆变器与母线的连线阻抗存在差异,因而功率就难以严格均分。
由式(1)、式(2)可知,若Zi∠θi为感性,则在稳态时,有功功率与相角有关,无功功率与电压有关,通过P-ω、Q-V下垂控制可分别调节有功、无功输出[6-7,10-11];若Zi∠θi为阻感性,则在稳态时,有功、无功之间存在耦合,需进行解耦控制,传统的P-ω、Q-V下垂法不再适用,同时逆变器与母线之间连线阻抗的不平衡也影响了功率的均分。因此,必须对输出阻抗进行优化,使逆变器的等效输出阻抗近似为感性,同时减小各并联逆变器输出阻抗与线路阻抗的差异,提高功率均分精度,减小系统环流。
1.3 dq坐标系下的虚拟阻抗设计
在传统并联控制器中加入虚拟电感,可使逆变器输出阻抗感性增强,即R/X变小,提高了有功、无功的解耦控制精度,同时还可抑制并联逆变器间的无功环流[3,8]。另外,虚拟电阻的加入,增加了系统的阻尼,能有效抑制系统振荡[6]。加入虚拟阻抗后,实现了对系统等效线路阻抗的间接控制,可表示为
(6)

(7)
(8)
式中:Rvir、Lvir分别为虚拟电阻和虚拟电感;Vorefd和Vorefq为输出电压调整参考值的d、q分量;ω为dq坐标系的旋转角频率。
在dq旋转坐标下实现虚拟阻抗如图2所示。
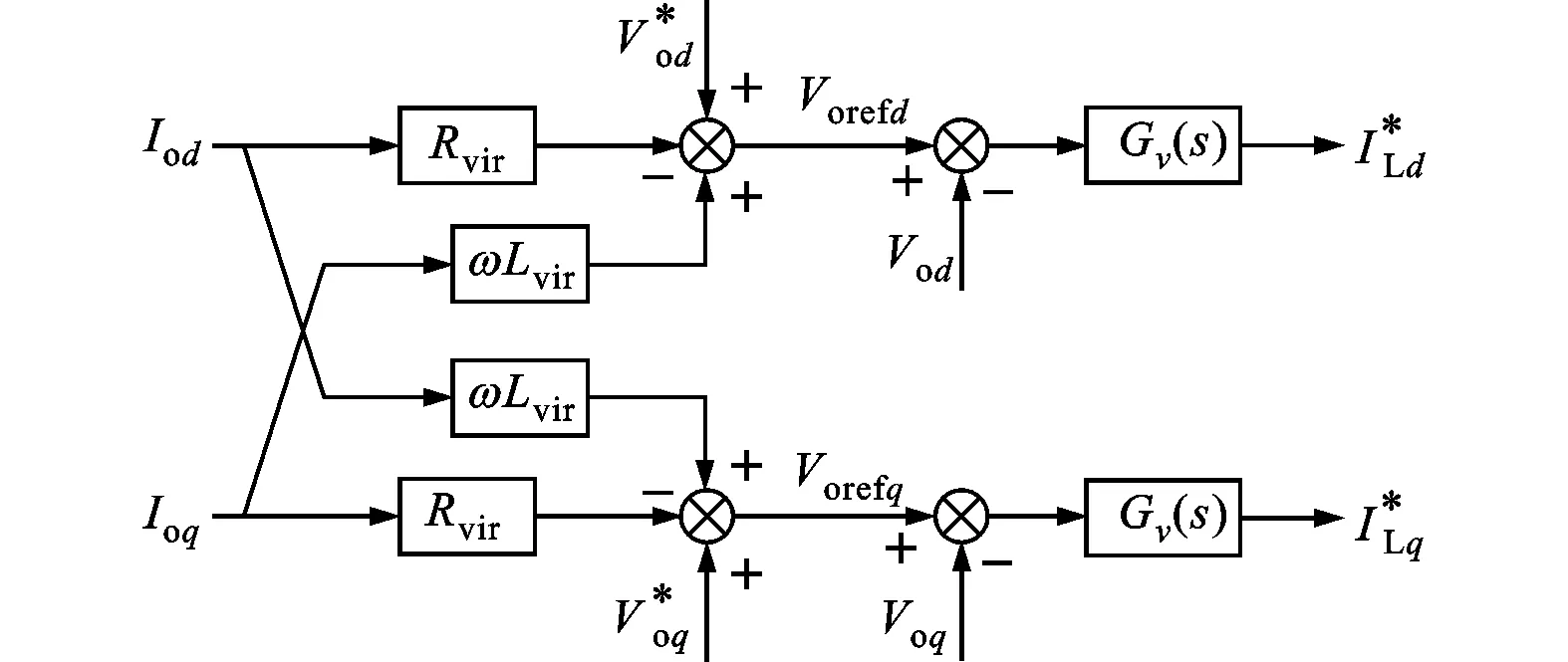
Vod、Voq分别为输出电压反馈值的d、q分量;Gv(s)为电压环PI调节器的传递函数分别为电流环参考值的d、q分量
2 功率与电压均衡控制策略
2.1 逆变器的输出电压外特性分析
图3为加入虚拟阻抗的逆变器控制框图,逆变器采用电压、电流双环控制,电压外环采用PI调节器,其传递函数为Gv(s),其输出作为电感电流内环的参考输入,传递函数为Gi(s)。
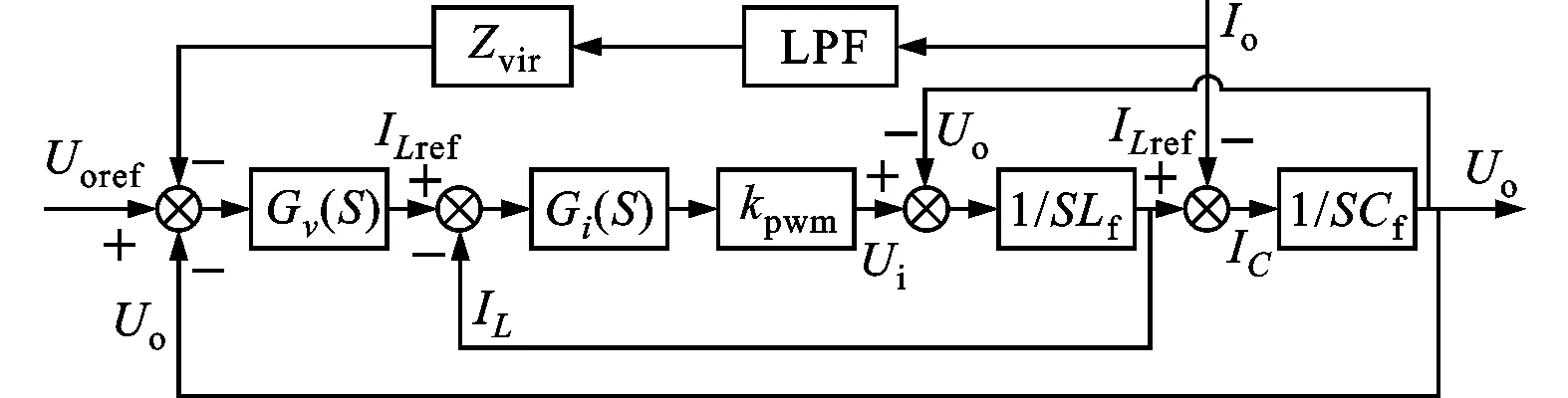
Uo为逆变器输出电压;Uoref为输出电压参考值;Lf和Cf分别为逆变器的输出LC滤波电感和电容;kpwm为PWM环节的比例系数;IL、IC和Io分别为滤波电感电流、滤波电容电流和输出电流
由图3可推导出逆变器的输出电压为
Uo(s)=G(s)[Uoref(s)-Zvir(s)Io(s)]-Zo(s)Io(s)
(9)
式中


将式(9)整理后,得
Uo(s)=G(s)Uoref(s)-Io(s)[G(s)Zvir(s)+Zo(s)]
(10)
加入虚拟阻抗后,总的输出阻抗为
Zovir(s)=G(s)Zvir(s)+Zo(s)
(11)

从式(9)和式(10)可以看出,逆变器的输出电压由两部分决定。一是跟踪输入给定量的部分G(s),其性能决定了输出量对给定量的跟踪性能。通过分析G(s)可知,与输出电压成正相关的参数为逆变器增益kpwm,与输出电压成负相关的参数有输出滤波电容和电感,即当输出滤波电感和电容过大时,会导致输出电压严重偏离额定值。二是逆变器的闭环输出阻抗Zovir(s)。采用下垂控制的逆变器,其输出阻抗同时受到线路阻抗、输出滤波器及控制参数的影响[4,6,8],且输出阻抗随滤波电感和虚拟阻抗的增加而增加,随滤波电容的增加而减小。当逆变器的主电路及控制参数确定后,G(s)基本保持不变,Zovir(s)主要由虚拟阻抗决定,因此虚拟阻抗的加入改变了输出阻抗的特性,使其感性增强,幅值增大,在传统下垂控制下提高了P、Q解耦控制精度,减小了系统环流。
2.2 电压和频率控制策略
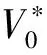

(a)Q-V (b)P-ω
为了实现微网的基本控制目标,即保证各并联逆变器均分负载功率且逆变器的输出电压幅值和频率保持额定输出,当功率变化引起电压和频率变化时,需对逆变器输出电压幅值和频率进行动态调节。结合图4和式(3)可知,要想对输出电压及频率进行调节,可通过改变下垂系数或Vn、ωn来达到目的。本文提出通过改变输出电压额定值Vn和频率额定值ωn来实现。即当负载功率增加(减小)引起电压幅值和频率降低(升高)时,可通过增加(减小)电压和频率的额定值来保持输出不变,在坐标图中表现为将原下垂曲线竖直向上或向下平移ΔVn(或Δωn),以此来补偿电压和频率由于下垂产生的偏差,使系统达到新的稳态,如图5所示。

(a)Q-V (b)P-ω


(12)
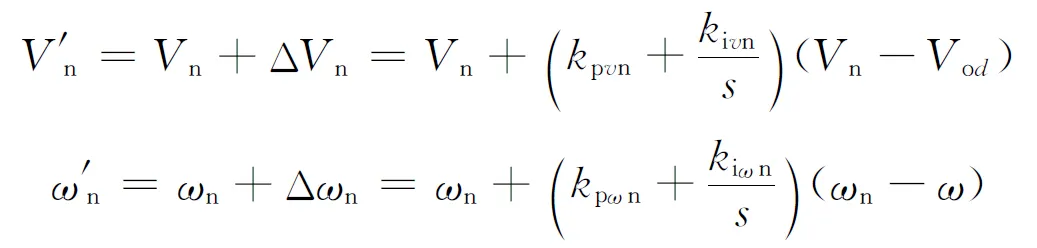


图6 输出电压调节框图

图7 频率调节框图
结合式(3)及图5,由于下垂控制固有的特性,即频率、电压与有功、无功互相影响,当逆变器空载运行时,由于输出功率为0,其输出电压和频率均为额定值。当逆变器带负载运行时,其实际输出电压和频率将小于额定值,如图5中,逆变器在下垂曲线②的作用下运行,工作点为b(V0,Q0),但V0 图8 功率与电压均衡控制流程图 当系统检测到逆变器输出功率发生较大降落(第二台逆变器投入或负载突然切除)且功率均分未完成时,令k=0,电压和频率的补偿开关断开,暂停对电压和频率的补偿调节,避免下垂与补偿调节产生耦合,下垂曲线回到曲线②,逆变器输出无功从Q0逐渐减小,对应电压从V0逐渐增大,但始终小于Vn。当系统检测到功率均分完成后,令k=1,闭合电压和频率补偿开关,经过微调,将Vn向上平移ΔVn1,得到下垂曲线③,系统达到稳态,工作点为c(Vn,Q1)。 由于两台逆变器参数相同,故其输出电压保持同步,都达到Vn,两台逆变器均分功率,均为Q1=Q0/2。系统对功率波动的监测是基于判断dQ/dt及dP/dt的大小进行的。当另一台逆变器切除或突增负载导致逆变器输出功率突增时,电压调节过程与上面相似,同样可得相同情况下的频率调节原理,实现流程如图8所示。这样,通过下垂控制与电压和频率补偿调节的分时作用,避免了二者产生耦合,互相影响,达到了并联系统功率合理分配和保持较高电能质量的目的。 为验证本文采用的并联控制算法的有效性,使用PSIM仿真软件搭建了两台逆变器并联模型,仿真模型参数设置见表1。 表1 本文模型仿真参数 仿真过程为:首先由一台逆变器单独带负载运行,在0.1s时,逆变器2通过交流母线并入,两台逆变器并联运行,共同提供负载功率。采用未加虚拟阻抗的传统双环控制策略和本文提出的控制策略进行两次仿真,仿真结果如图9所示。 (a)传统控制方法下逆变器输出的有功功率 (b)本文控制方法下逆变器输出的有功功率 (c)传统控制方法下逆变器输出的无功功率 (d)本文控制方法下逆变器输出的无功功率 (e)本文控制方法下的逆变器输出电流 (f)本文控制方法下的逆变器输出电压 (g)本文控制方法下的逆变器输出频率 由图9a~图9d可知,由于两逆变器与母线之间线路阻抗的差异,采用传统双环控制时逆变器有功、无功功率不能较好地均分。加入虚拟阻抗环后,逆变器输出有功和无功功率能够较好地均分,且动态响应快。 另外,加入本文所提的电压和频率补偿环节后,逆变器1单独带负载运行时,由于下垂特性和虚拟阻抗的作用,电压和频率与额定值相比有较小的偏差。采用电压和频率调节策略,通过实时增大Vn和ωn,逆变器的输出电压和频率都维持在额定值。在0.1s时,逆变器2并入,逆变器1的输出功率迅速减小,系统快速响应,并暂停电压和频率的补偿调节,切换到采用虚拟阻抗的P-ω、Q-V传统下垂控制。通过分别调节电压和频率,有功、无功功率得到独立控制,两台逆变器的输出有功、无功功率迅速达到均分,且基本消除了系统环流。在此过程中,逆变器1的输出电压和频率由于没有了补偿调节,在下垂特性的作用下,电压和频率都小于额定值,且随着逆变器输出功率的减小,电压和频率逐渐接近额定值。当功率均分完成后,系统重新启动电压幅值和频率调节,在大约4个周期之后,两台逆变器的电压幅值和频率都恢复到额定值,且基本无环流,响应速度较快。 本文基于实验室的两台逆变器并联系统进行了实验验证,并与仿真结果进行对比,逆变器容量为1kV·A,其他参数如表2所示。 表2 本文模型实验参数 与仿真过程相同,分别采用未加虚拟阻抗的传统双环控制策略和本文提出的控制策略进行两组试验,实验结果如图10所示。 (a)传统双环控制下的逆变器输出有功功率 (b)本文控制方法下的逆变器输出有功功率 (c)传统双环控制下的逆变器输出无功功率 (d)本文控制方法下的逆变器输出无功功率 (e)本文控制方法下的逆变器输出电流 (f)本文控制方法下的逆变器输出电压 (g)本文控制方法下的逆变器频率 从图10a和图10b可以看出,与仿真波形相似,采用传统的未加虚拟阻抗的双环控制时,并联逆变器的输出有功功率不能准确均分,P1、P2大约相差0.2 kW,而加入虚拟阻抗后,有功功率均分较好。从图10c和图10d可以看出,未加入虚拟阻抗时,两逆变器输出无功功率也存在偏差,而加入虚拟阻抗后,无功功率也能较好地均分。 采用本文算法的实验过程如下。逆变器1单独带负载运行,提供给负载有功、无功功率,根据下垂特性,其电压和频率会小于额定值,但采用本文算法对电压和频率的参考值进行动态调节,电压和频率始终保持在额定值,见图10f、图10g(图10f为逆变器1的a相电压)。在某一时刻,投入逆变器2,由两台逆变器并联运行,均分负载功率,因此逆变器1的输出功率迅速减小,系统通过判断开关,暂停对电压和频率的补偿调节,切换到传统下垂控制模式下,逆变器1的电压和频率迅速降低到额定值以下,且随着输出功率减小,其电压幅值和频率逐渐增大,但维持在额定值以下。同时,采用含有虚拟阻抗的控制策略,实现有功、无功的解耦控制,使两台逆变器均分负载功率,由图10b、图10d、图10e(图10e为两台逆变器的a相电流)可以看出,功率均分精度较高,动态响应较快。当系统检测到功率均分完成后,重新切换到电压和频率补偿调节模式,逐渐微调电压和频率恢复到额定值,两台逆变器输出电压相同,功率保持均分,环流较小,提供较高的电能质量。 虚拟阻抗的应用改变了逆变器的输出阻抗特性,有效抑制了线路参数差异对功率分配造成的影响,提高了并联逆变器的输出功率均分精度。在微电网孤岛运行时,提出的控制策略弥补了传统逆变器并联技术的不足,实现了电压和频率的二次调节,使微电网孤岛运行时电压和频率维持在额定值,保持较高的电能质量,实现了微电网孤岛运行时并联逆变器的功率与电压均衡控制,具有较高的使用价值。 [1] 陈宏志, 王旭, 刘建昌. 基于虚拟电阻匹配模式的逆变器并联方案 [J]. 中国电机工程学报, 2012, 32(6): 24-32. CHEN Hongzhi, WANG Xu, LIU Jianchang. Current sharing method for parallel inverters based impedance matching mode [J]. Proceedings of the CSEE, 2012, 32(6): 24-32. [2] SHI Hongtao, ZHUO Fang, HOU Lixiang, et al. Small-signal stability analysis of a microgrid operating in droop control mode [C]∥2013 IEEE Energy Conversion Congress and Exposition Asia. Piscataway, NJ, USA: IEEE, 2013: 882-887. [3] GUERRERO J M, VICUNA L G, MATAS J, et al. Output impedance design of parallel-connected UPS inverters with wireless load-sharing control [J]. IEEE Transactions on Industrial Electronics, 2005, 52(4): 1126-1135. [4] SHI Hongtao, YANG Zhen, YUE Xiaolong, et al. Calculation and measurement of harmonic impedance for a microgrid operating in islanding mode [C]∥2012 7th International Power Electronics and Motion Control Conference. Piscataway, NJ, USA: IEEE, 2012: 356-361. [5] MOHAMED Y A R I, EL-SAADANY E F. Adaptive decentralized droop controller to preserve power sharing stability of paralleled inverters in distributed generation microgrids [J]. IEEE Transactions on Power Electronics, 2008, 23(6): 2806-2816. [6] YAO Wei, CHEN Min, MATAS J, et al. Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing [J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 576-587. [7] 姚玮, 陈敏, 陈晶晶, 等. 一种用于无互连线逆变器并联的多环控制方法 [J]. 电工技术学报, 2008, 23(1): 84-89. YAO Wei, CHEN Min, CHEN Jingjing, et al. An improved wireless control strategy for parallel operation of distributed generation inverters [J]. Transactions of China Electrotechnical Society, 2008, 23(1): 84-89. [8] HE Jinwei, LI Yunwei. Analysis, design, and implementation of virtual impedance for power electronics interfaced distributed generation [J]. IEEE Transactions on Industrial Applications, 2011, 47(6): 2525-2538. [9] GUERRERO J M, DE VICUNA L G, MATAS J, et al. A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems [J]. IEEE Trans on Power Electronics, 2004, 19(5): 1205-1213. [10]姚玮, 陈敏, 牟善科, 等. 基于改进下垂法的微电网逆变器并联控制技术 [J]. 电力系统自动化, 2009, 33(6): 77-80. YAO Wei, CHEN Min, MOU Shanke, et al. Paralleling control technique of microgrid inverters based on improved droop method [J]. Automation of Electric Power Systems, 2009, 33(6): 77-80. [11]张庆海, 彭楚武, 陈燕东, 等. 一种微电网多逆变器并联运行控制策略 [J]. 中国电机工程学报, 2012, 32(25): 126-132. ZHANG Qinghai, PENG Chuwu, CHEN Yandong, et al. A control strategy for parallel operation of multi-inverters in microgrid [J]. Proceedings of the CSEE, 2012, 32(25): 126-132. [12]王成山, 肖朝霞, 王守相. 微网综合控制与分析 [J]. 电力系统自动化, 2008, 32(7): 98-103. WANG Chengshan, XIAO Zhaoxia, WANG Shouxiang. Synthetical control and analysis of microgrid [J]. Automation of Electric Power Systems, 2008, 32(7): 98-103. [13]周念成, 金明, 王强钢, 等. 串联和并联结构的多微网系统分层协调控制策略 [J]. 电力系统自动化, 2013, 37(12): 13-18. ZHOU Niancheng, JIN Ming, WANG Qianggang, et al. Hierarchical coordination control strategy for multi-microgrid system with series and parallel structure [J]. Automation of Electric Power Systems, 2013, 37(12): 13-18. [14]王永刚. 基于下垂控制的微网频率稳定性分析 [D]. 北京: 华北电力大学, 2012. [15]张东, 卓放, 师洪涛, 等. 分布式发电系统三相变流器软件锁相环设计 [J]. 电力电子技术, 2013, 47(10): 43-45. ZANG Dong, ZHUO Fang, SHI Hongtao, et al. Design of the software phase locked loop for the three phase converter in distributed power generation system [J]. Power Electronics, 2013, 47(10): 43-45. (编辑 杜秀杰) BalancedControlStrategyforParalleledInverterPowerandVoltageinIslandedMicro-Grid GENG Zhiqing,ZHUO Fang,NING Gaidi,SHI Hongtao,ZHANG Dong,ZHAI Hao (School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China) Considering the low power allocation accuracy of paralleled inverters system using traditional double-loop control and the voltage and frequency deviations caused by droop control in micro-grid, the power allocation mechanism and output voltage characteristics of a parallel system are discussed, and a balanced control strategy of power and voltage for inverters parallel operation is proposed based on virtual impedance and instantaneous output voltage/frequency regulation. Virtual impedance is added to existing control loops to improve the characteristics of output impedance, and the power allocation accuracy is enhanced withP-ω,Q-Vdroop control. A scheme for regulating output voltage magnitude and frequency also participates in the loops to exert secondary regulation on the voltage and frequency deviations from droop control, and the higher output voltage quality remains. The simulation and experiment demonstrate that the proposed balanced control strategy for power and voltage makes the paralleled inverters share the load power better and preserves the rated output voltage and frequency in islanded micro-grid. micro-grid; paralleled inverters; power sharing; voltage/frequency regulation; balanced control 2014-03-23。 耿志清(1989—),男,硕士生;卓放(通信作者),男,教授。 国家自然科学基金资助项目(51177130);国家高技术研究发展计划资助项目(2012AA050206)。 时间:2014-07-28 10.7652/xjtuxb201412007 TM464 :A :0253-987X(2014)12-0041-08 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140728.1036.002.html
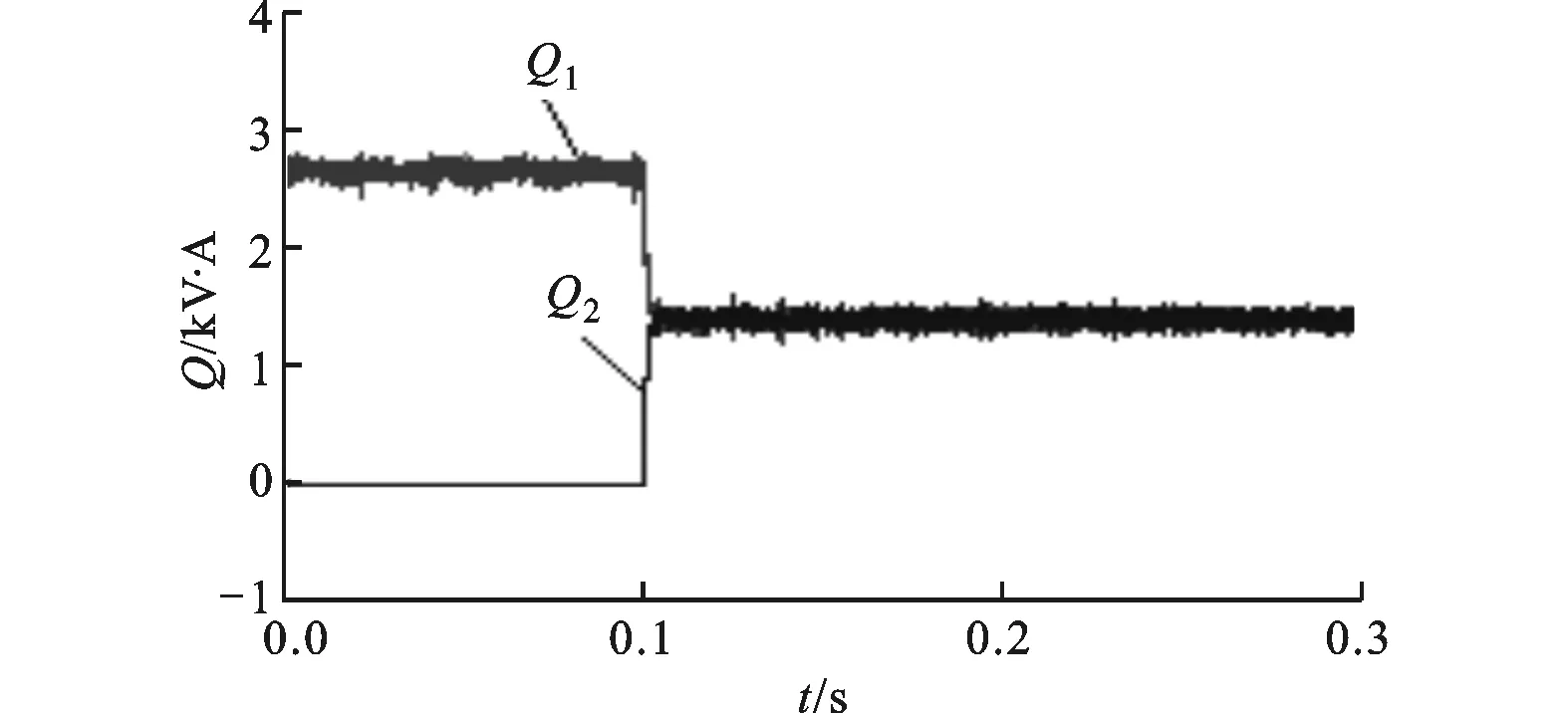
3 仿 真







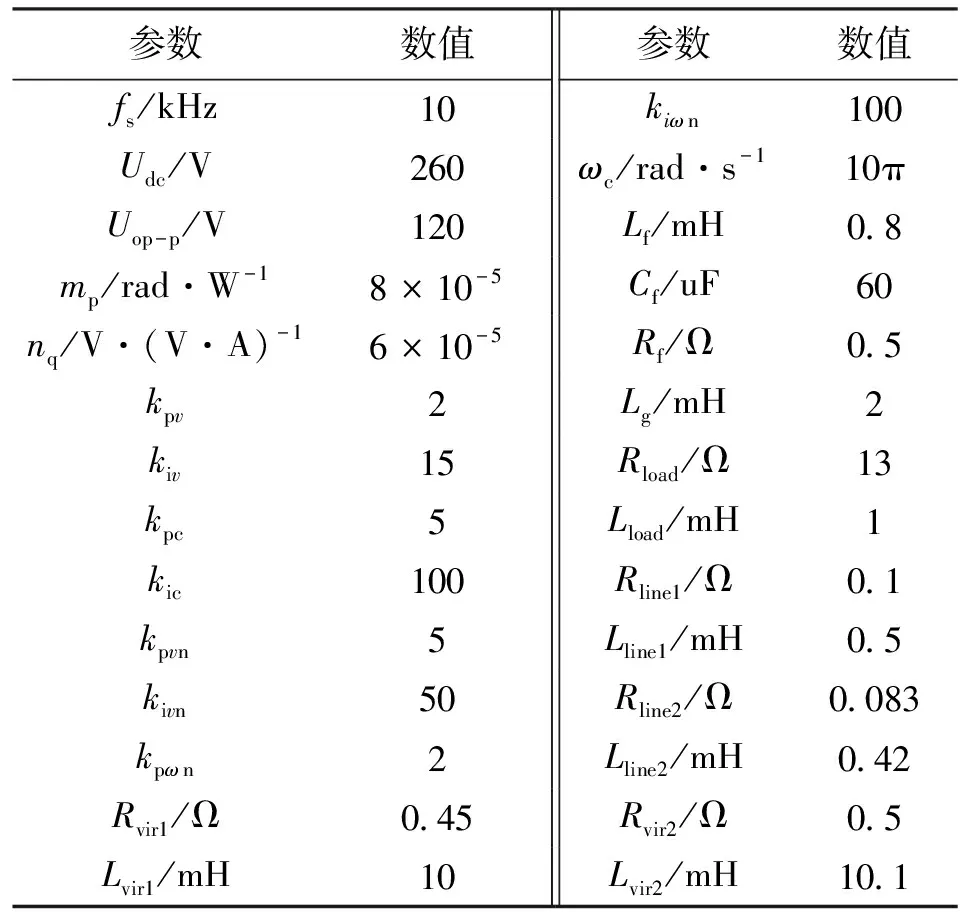
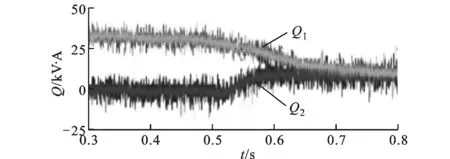
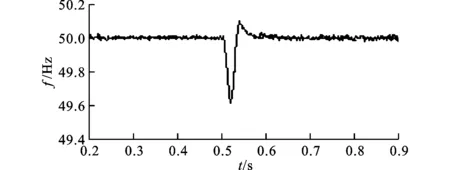
4 实 验





5 结 论

