Heusler合金Sc2VZ (Z=C,Si,Ge,Sn,Pb)半金属铁磁性的第一性原理研究
刘兴军,王正伟,许伟伟,韩佳甲,王翠萍
(厦门大学材料学院,福建 厦门 361005)
自旋电子学是一门以研究电子的自旋极化输运特性以及基于这些特性设计、开发新型电子器件为主要内容的交叉学科.它在信息存储领域具有广阔的应用前景,因而受到学术界和工业界的广泛关注[1].目前自旋电子学所遇到的关键问题之一是如何高效地将自旋电流从铁磁性材料注入到半导体材料之中.而半金属Heusler合金因具有独特的电子结构,即一种自旋方向的能带呈现金属性,另一种自旋方向的能带呈现半导体性,从而使得费米能级附近的传输电子的自旋极化率为100%,被认为是理想的半导体自旋电流注入源[2].另外,Heusler合金还具有较高的居里温度、较大的磁矩,而且它们与广泛应用的闪锌矿结构二元半导体有着相似的晶体结构[3-4].
早在20世纪80年代,de Groot等[5]便预测出半Heusler合金MnNiSb具有半金属性.不久,Kübler等[6]预测出全Heusler合金Co2MnSn和Co2MnAl也具有半金属性.在随后的基于密度泛函理论的研究中,一些Mn-基[4,7]、Fe-基[8-9]、Ru-基[10-11]、V-基[12]、Co-基[13-14]、Cr基[15-16]Heusler合金也被预测出具有半金属性.基于这些理论研究,研究者开始围绕着Heusler合金的磁性以及输运性能开展大量的实验研究,一些Heusler合金现已成功地应用于自旋电子器件中.例如,Co2MnGe应用于电流垂直平面巨磁阻自旋阀中的铁磁层材料[17],Co2VAl也应用于隧穿磁阻结[18-19].
近年来,研究人员发现一些Sc基Heusler合金也具有半金属性[20-21].据报道,Hg2CuTi结构的Sc2CrZ (Z=Si,Ge,Sn) Heusler合金半金属性的产生主要是由于3d过渡金属Sc和Cr原子的d态电子之间强烈的杂化作用[20]所致.在Sc2MnZ (Z=Si,Ge,Sn) Heusler合金的研究中也得出了类似结论[21].由于过渡金属元素V,Cr和Mn作为相近邻的元素通常会表现出相似的物理性质,因此有必要对Sc2VZ (Z=C,Si,Ge,Sn,Pb) 合金开展研究工作.目前除了Sc2VSi Heusler合金被报道具有半金属性以外[22],还没有关于Sc2VZ (Z=C,Ge,Sn,Pb) Heusler合金的研究报道.本研究将采用第一性原理的方法对Sc2VZ (Z=C,Si,Ge,Sn,Pb) Heusler合金的电子结构以及磁学性能展开系统的研究.
1 理论模型和计算方法
1.1 理论模型
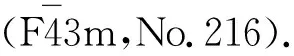

图1 Hg2CuTi型Sc2VZ (Z=C,Si,Ge,Sn,Pb) Heusler合金的晶体结构Fig.1 Hg2CuTi-prototype structure of Sc2VZ (Z=C,Si,Ge,Sn,Pb) Heusler compounds
1.2 计算方法
本研究基于密度泛函理论的投影缀加波方法 (PAW),采用第一性原理计算软件包VASP进行计算[25].交换关联能采用 Perdew和Wang (PW91) 提出的广义梯度近似 (GGA) 来处理[26].平面波截断能为450 eV,k网格点采用Monkhorst-Pack方法产生,弛豫和静态计算采用19×19×19个k网格点,态密度和能带结构计算采用21×21×21个k网格点.体系每个单胞总能的收敛值取10-5eV.
2 结果与讨论
2.1 晶体结构优化与形成能
为了获得Heusler合金的平衡基态,首先计算了Sc2VZ Heusler合金分别在铁磁态和非铁磁态下,总能随晶格常数的变化情况.计算得到的Sc2VZ (Z=C,Si,Ge,Sn,Pb) 在不同磁态下总能随晶格常数的变化曲线如图2所示.由图2可见,在本研究计算的晶格常数范围内,Sc2VZ (Z=C,Si,Ge,Sn,Pb) 合金铁磁态下的总能比非铁磁态下的总能低,因而Sc2VZ (Z=C,Si,Ge,Sn,Pb) 合金的稳定态为铁磁态.将不同晶格常数下计算得到的Sc2VZ (Z=C,Si,Ge,Sn,Pb) 铁磁态下的总能E(V)和体积V由Murnaghan状态方程[27]进行拟合,得到的Sc2VZ (Z=C,Si,Ge,Sn,Pb) Heusler合金的平衡晶格常数、体弹性模量列于表1中.如表1所示,计算得到的Sc2VSi晶格常数值与Skaftouros等报道的结果[22]十分接近 (仅有0.49%的差异).
另外,由于形成能可以反映合金化合物的热力学稳定性,本研究还计算了Sc2VZ (Z=C,Si,Ge,Sn,Pb) Heusler合金的形成能ΔH,其可定义为:
ΔH(Sc2VZ)=1/4[Etotal(Sc2VZ)-
2Esolid(Sc)-Esolid(V)-Esolid(Z)],
(1)
其中,Etotal(Sc2VZ),Esolid(Sc/V/Z) 分别表示Sc2VZ化合物和各纯组元 (Sc,V和Z元素) 的稳定态在0 K下的静态能量.纯组元Sc元素的稳定态为密排六方结构,V元素的稳定态为体心立方结构,C元素的稳定态为石墨结构,Si、Ge和Sn元素的稳定态为金刚石晶格,Pb元素的稳定态则为面心立方结构.由式 (1) 计算得到的Sc2VZ (Z=C,Si,Ge,Sn,Pb) Heusler合金的形成能ΔH列于表1中.如表1所示Sc2VZ (Z=Si,Ge,Sn,Pb) 的形成能为负值,表明Sc2VZ (Z=Si,Ge,Sn,Pb)具有一定的热力学稳定性.而Sc2VC的形成能为正值,表明Sc2VC在热力学上是不稳定的,本文将不再对Sc2VC的电子结构和磁性作进一步研究.
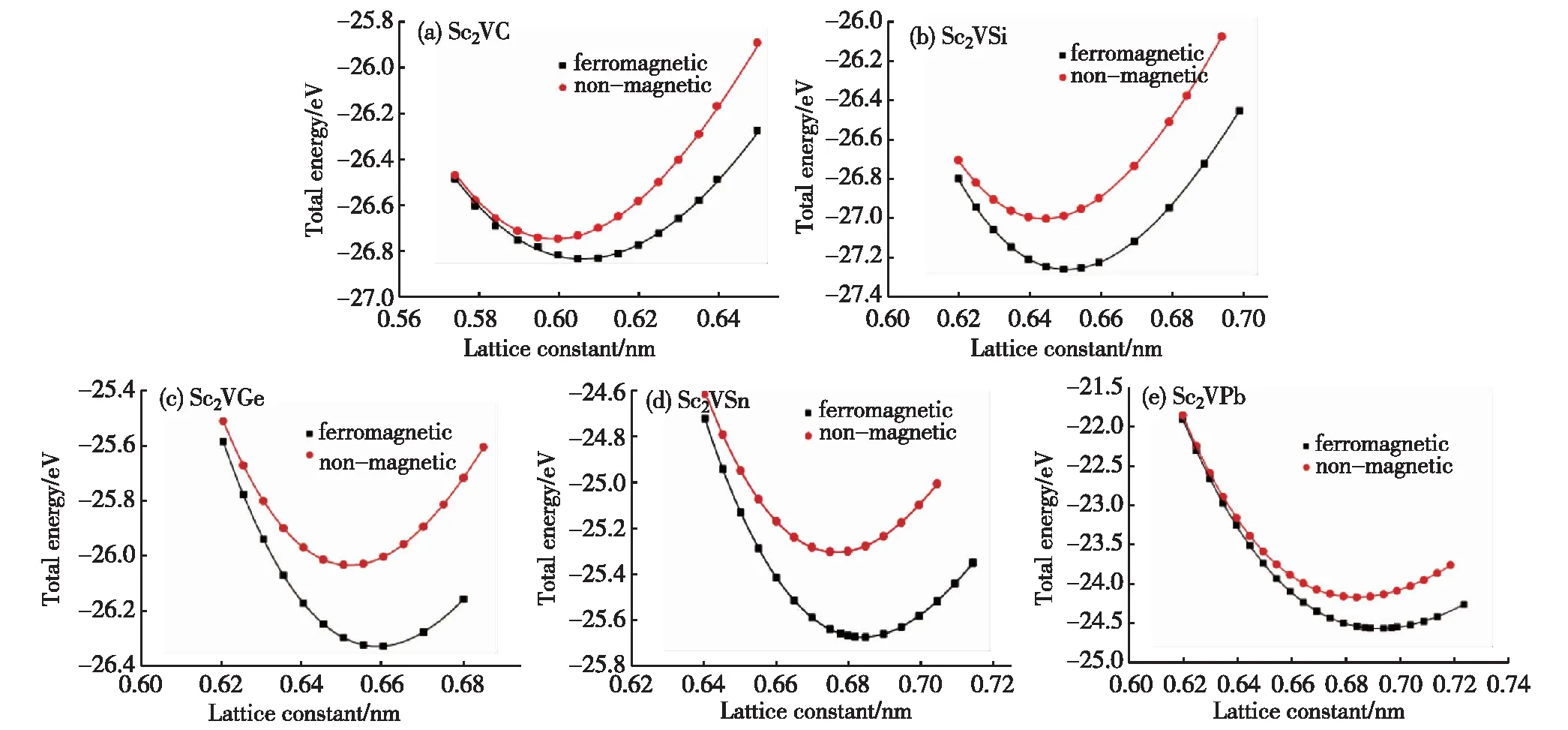
图2 在铁磁态和非铁磁态下总能随晶格常数的变化曲线Fig.2 Calculated total energy as a function of lattice constants in both the non-magnetic and ferromagnetic states
2.2 电子结构与半金属带隙产生的原因
为了研究Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金的电子结构,本文计算了布里渊区中沿高对称点方向的能带结构.计算得到的自旋向上 (Majority) 和自旋向下 (Minority) 的能带结构以及对应的总态密度如图3所示.
图3中水平黑色的虚线表示费米能级(Ef=0 eV).从图3中可以看出,Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金的费米能级 (Ef=0 eV) 均位于自旋向上轨道的带隙中.在这种独特的电子结构中,自旋向上态表现出半导体性,自旋向下态则表现出金属性,表明Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金具有半金属铁磁性.在半金属性Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金电子结构中,费米能级Ef处电子的自旋极化率定义为:
(2)
其中,符号↑和↓分别表示自旋向上态和自旋向下态,半金属带隙宽度 (Egap) 定义为自旋向上态中的导带底 (ECBM) 与价带顶 (EVBM) 之间的能量差值.自旋反转带隙 (Eflip) 定义为自旋向上态中价带顶 (EVBM) 与费米能级Ef之间的差值,表示将自旋向上态电子从价带顶反转至费米能级所需要的能量.表2列出了Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金的Egap,Eflip,ECBM以及EVBM.从表2中看出,随着IV A族元素的原子序数逐渐增大 (从Si到Pb),Eflip缓慢增大,而ECBM和EVBM则在缓慢减小.另外,如表2所示,Sc2VSi,Sc2VGe和Sc2VSn三者的Egap比较接近,都在0.35 eV左右;然而Sc2VPb的Egap只有0.173 eV,明显小于其他3种合金.但是根据图3 (d) 中Sc2VPb的总态密度图,Sc2VPb自旋向上态中费米能级附近的态密度值极小.我们可以近似认为Sc2VPb具有与Sc2VSi,Sc2VGe和Sc2VSn相当宽度的带隙.它们这种相对较宽的带隙值表明其半金属特性具有一定的稳定性,一些细小的物理量 (例如,晶格常数) 的改变不会将费米能级移出自旋向上态的带隙.需要说明的是,传统的GGA方法可能对某些含有d-d或f-f态强关联体系的带隙值会低估,而GGA+U方法可修正强关联体系电子结构,使其很好地符合实验数据,而且通常GGA+U方法计算的带隙值会比GGA的带隙值大.但是由于本研究更为关注的是体系是否具有半金属性,半金属性的判定依据是体系电子结构是否具有半金属性带隙,如果通过GGA方法计算出体系具有半金属带隙,那么GGA+U方法计算的结果仍然能够说明体系具有半金属性.另外,本研究是理论预测性研究,尚没有实验值比对,无法确定可靠的U值参数进行GGA+U计算,因而本文没有采用GGA+U方法来计算体系的电子结构,而是采用了传统的GGA方法,该方法已经被广泛用于其他半金属体系的研究中[4,9,13-16,20-21].

表1 Sc2VZ (Z=C,Si,Ge,Sn,Pb) 合金的晶格常数a0、体弹性模量B0和热力学形成能ΔHTab.1 The calculated equilibrium lattice constants a0, bulk modulus B0 and formation enthalpy ΔH for Sc2VZ (Z=C,Si,Ge,Sn,Pb) Heusler compounds

(a) Sc2VSi;(b) Sc2VGe;(c) Sc2VSn; (d) Sc2VPb; TDOS为总态密度.图3 能带结构及总态密度Fig.3 Spin-resolved electronic band structures together with the total density of states
ρ↑(Ef) 和ρ↓(Ef) 分别表示费米能级处自旋向上态和自旋向下态的态密度值.如图3所示,Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金在费米能级处ρ↑(Ef)等于0,因而由式 (2) 计算得到它们在费米能级处的传输电子的自旋极化率P=100%,表明只有单自旋电子参与这些Heusler合金电子输运过程.
为了更清楚地理解Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金半金属带隙的形成机理,本文计算了总态密度和分波态密度,如图4所示.图4中垂直虚线表示费米能级Ef,符号↑和↓分别表示自旋向上态和自旋向下态.由图4可见,Sc2VZ (Z=Si,Ge,Sn,Pb)Heusler合金总态密度中的低能量部分 (-8 eV以下) 主要来自Z (Z=Si,Ge,Sn,Pb) 原子的s态电子分波态密度的贡献.这些能量较低的价带与其他价带之间由带隙隔开,因而Z原子的s态电子对半金属带隙的形成以及磁性几乎没有影响.总态密度中-5~-2 eV的区域主要来自Z原子的p态电子的贡献.而总态密度中-2~4 eV能量区域主要由Sc,V原子的d态电子贡献.在Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金电子自旋向上的态密度中,费米能级附近存在4个较强的杂化峰.其中,费米能级以下 (-2~0 eV) 的2个杂化峰主要由V-d态贡献,而费米能级以上 (0~1.5 eV) 的2个杂化峰则主要由Sc1-d态贡献.由图4可以看出,Sc1-d态、Sc2-d态和V-d态在-2~4 eV能量区域内相互交叠,表明Sc1-d态、Sc2-d态和V-d态存在强烈的轨道杂化作用.

表2 平衡晶格常数下的Sc2VZ (Z=Si,Ce,Sn,Pb)的能量值Tab.2 The energy values for Sc2VZ (Z=Si,Ge,Sn,Pb) compounds at equilibrium lattice constant eV

(a) Sc2VSi;(b) Sc2VGe;(c) Sc2VSn;(d) Sc2VPb.图4 总态密度及分波态密度Fig.4 The calculated total density of states and partial density of states plots
Sc1和V原子是最近邻位置,它们之间的杂化作用很强,Sc1-d轨道和V-d轨道之间的杂化示意图如图5 (a) 所示,其中d1、d2、d3、d4、d5分别对应dxy、dyz、dxz、dz2、dx2-y2,杂化生成能量较低的成键态(2×eg、3×t2g) 与能量较高的反键态 (2×eu、3×tu).能量较低的Sc1-V成键态轨道 (2×eg、3×t2g) 继续与Sc2原子的d轨道杂化,最终形成成键态的eg、t2g轨道和反键态的eg、t2g轨道,如图5 (b) 所示;另外,eu和t1u轨道没有与Sc2的d轨道发生杂化而保留下来[20,30-31].费米能级刚好也被移到能隙之间,因而自旋向上态中的半金属性带隙是由于Sc1-d,Sc2-d,V-d态轨道之间强烈的杂化作用产生的.
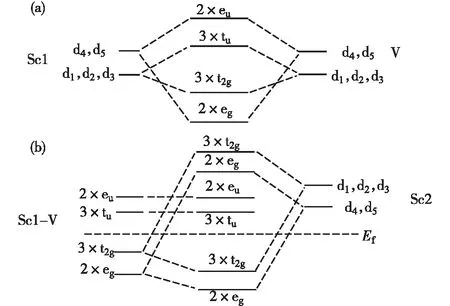
(a) Sc1-V d轨道之间的杂化; (b) Sc1-V与Sc2 d轨道之间的杂化.图5 Sc2VZ自旋向上 d轨道杂化示意图Fig.5 The hybridization between the d-state of Sc2VZ Heusler compounds
2.3 晶格常数的变化对半金属性的影响
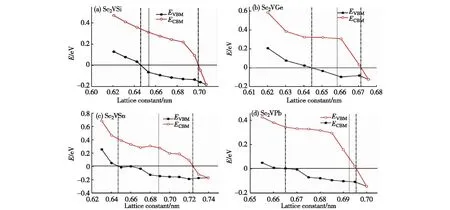
图6 Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金中自旋向上态带隙随晶格常数的变化曲线Fig.6 The majority band gaps of Sc2VZ (Z=Si,Ge,Sn,Pb) compounds as a function of lattice constants
Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金半金属带隙随晶格常数的变化情况如图6所示.水平实线和垂直虚线分别表示费米能级和平衡晶格常数.红圈和黑圈分别表示自旋向上态中导带底与价带顶的能量值.从图6可见,随着晶格常数的逐渐增大,Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金半金属带隙宽度逐渐减小.一方面,随着晶格常数逐渐增大,价带顶以及导带底均逐渐降低,但是导带底在最后阶段会急剧下降,当导带底下降到费米能级Ef以下时,半金属性随即消失.另一方面,随着晶格常数逐渐减小,当价带顶升高到费米能级以上时,半金属性也随即消失.由此可见,在2条垂直点划线之间的晶格常数范围内,费米能级位于半金属带隙中,即Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金分别在0.643~0.693,0.644~0.671,0.643~0.722和0.665~0.696 nm晶格常数范围内仍然保持着半金属特性.
2.4 磁性以及Slater-Pauling规则
据Ahmadian等报道,Sc2CrZ (Z=Si,Ge,Sn) Heusler合金的总磁矩能够很好地符合Slater-Pauling规则,即Mtot=18-Zt[20-21].其中,Mtot和Zt分别表示单原胞的总磁矩以及总价电子数.表3列出了计算得到Sc2VZ Heusler合金总磁矩以及各原子的自旋磁矩.Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金的总价电子数为15,其总自旋磁矩均为整数,即3.00 μB.因此,计算结果完全符合Slater-Pauling规则.

表3 Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金的总磁矩 (Mtot)、各原子磁矩 (Mi) 以及间隙区磁矩 (Mint)Tab.3 The calculated magnetic moments for Sc2VZ (Z=Si,Ge,Sn,Pb) compounds.Mtot:total magnetic moment; Mi(i=Sc,V and Z):partial magnetic moments for i atoms; Mint:magnetic moment in the interstitial region

(a) Sc2VSi;(b) Sc2VGe;(c) Sc2VSn;(d) Sc2VPb.图7 总磁矩以及各原子磁矩随晶格常数的变化曲线Fig.7 The total and partial magnetic moments as a function of lattice constants
本文还研究了Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金总磁矩和各原子的磁矩随晶格常数的变化情况,计算结果如图7所示.可见,在一个较宽的晶格常数变化范围内,Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金的总自旋磁矩近似保持整数值3.00μB.一定程度晶格常数的变化并不会明显地影响总自旋磁矩.然而Sc1,Sc2,V以及Z (Z=Si,Ge,Sn,Pb) 原子的分磁矩却明显受到晶格变形的影响.由图7和表3可知,Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金的总磁矩主要由Sc原子和V原子贡献,Z原子对总磁矩的贡献则很小.随着晶格常数的增大,Sc1和Sc2原子磁矩逐渐减小,而V原子磁矩则逐渐增大,从而使得原胞总磁矩能够在一定的晶格常数变化范围内保持为常数.
3 结 论
本文对Sc2VZ (Z=C,Si,Ge,Sn,Pb) Heusler合金进行了第一性原理研究,详细分析了它们的电子结构以及磁性.主要结论如下:
1) Sc2VZ (Z=C,Si,Ge,Sn,Pb) Heusler合金在基态下呈现铁磁性;
2) Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金具有一定的热力学稳定性,而Sc2VC不具有热力学稳定性;
3) Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金在平衡晶格常数下表现出半金属性,而且其半金属性在一定的晶格常数变化范围内保持稳定;
4) 计算得到Sc2VZ (Z=Si,Ge,Sn,Pb) Heusler合金的总磁矩符合Slater-Pauling规则,并且其总磁矩在一定的晶格常数变化范围内保持为常数.
[1] Fecher G H.Spintronics:from materials to devices [M].Germany:Springer Press,2013.
[2] Graf T,Felser C,Parkin S S P.Simple rules for the understanding of Heusler compounds [J].Progress in Solid State Chemistry,2011,39(1):1-50.
[3] Bergmann A,Grabis J,Toperverg B P,et al.Antiferromagnetic dipolar ordering in [Co2MnGe/V]Nmultilayers [J].Physical Review B,2005,72(21):214403.
[4] Xing N,Li H,Dong J,et al.First-principle prediction of half-metallic ferrimagnetism of the Heusler alloys Mn2CoZ(Z=Al,Ga,Si,Ge) with a high-ordered structure [J].Computational Materials Science,2008,42(4):600-605.
[5] de Groot R,Mueller F,van Engen P,et al.New class of materials:half-metallic ferromagnets [J].Physical Review Letters,1983,50(25):2024-2027.
[6] Kübler J,William A R,Sommers C B.Formation and coupling of magnetic moments in Heusler alloys [J].Physical Review B,1983,28(4):1745-1755.
[7] Liu G D,Dai X F,Liu H Y,et al.Mn2CoZ(Z=Al,Ga,In,Si,Ge,Sn,Sb) compounds:structural,electronic,and magnetic properties [J].Physical Review B,2008,77(1):014424.
[8] Fujii S,Ishida S,Asano S.A half-metallic band structure and Fe2MnZ(Z=Al,Si,P) [J].Journal of the Physical Society of Japan,1995,64(1):185-191.
[9] Luo H Z,Zhu Z Y,Ma L,et al.Electronic structure and magnetic properties of Fe2YSi(Y=Cr,Mn,Fe,Co,Ni) Heusler alloys:a theoretical and experimental study [J].Journal of Physics D:Applied Physics,2007,40(22):7121-7126.
[10] Ishida S,Kashiwagi S,Fujii S,et al.Magnetic and half-metallic properties of new Heusler alloys Ru2MnZ(Z=Si,Ge,Sn and Sb) [J].Physica B:Condensed Matter,1995,210(2):140-148.
[11] Deka B,Das R,Srinivasan A.Magnetic properties of Ge substituted Ru2FeSi alloys [J].Journal of Magnetism and Magnetic Materials,2013,347:101-104.
[12] Xing N,Gong Y,Zhang W,et al.First-principle prediction of half-metallic properties for the Heusler alloys V2YSb(Y=Cr,Mn,Fe,Co) [J].Computational Materials Science,2009,45(2):489-493.
[13] Barth J,Fecher G H,Balke B,et al.Itinerant half-metallic ferromagnets Co2TiZ(Z=Si,Ge,Sn):ab initio calculations and measurement of the electronic structure and transport properties [J].Physical Review B,2010,81(6):064404.
[14] Sargolzaei M,Richter M,Koepernik K,et al.Spin and orbital magnetism in full Heusler alloys:a density functional theory study of Co2YZ(Y=Mn,Fe;Z=Al,Si,Ga,Ge) [J].Physical Review B,2006,74(22):224410.

[16] Li J,Chen G,Li J,et al.The lower-valence coexisting ferrimagnetic Cr2VX(X=Ga,Si,Ge,Sb) Heusler compounds:a first-principles study [J].Scripta Materialia,2008,59(10):1107-1110.
[17] Nikolaev K,Kolbo P,Pokhil T,et al."All-Heusler alloy" current-perpendicular-to-plane giant magnetoresistance [J].Applied Physics Letters,2009,94(22):222501-222508.
[18] Chadov S,Graf T,Chadova K,et al.Efficient spin injector scheme based on Heusler materials [J].Physical Review Letters,2011,107(4):047202-047208.
[19] Karthik S V,Rajanikanth A,Takahashi Y K,et al.Microstructure and spin polarization of quaternary Co2Cr1-xVxAl,Co2V1-xFexAl and Co2Cr1-xFexAl Heusler alloys [J].Acta Materialia,2007,55(11):3867-3874.
[20] Ahmadian F,Alinajimi R.First-principles study of half-metallic properties for the Heusler alloys Sc2CrZ(Z=C,Si,Ge,Sn) [J].Computational Materials Science,2013,79(11):345-351.
[21] Ahmadian F,Salary A.Half-metallicity in the inverse Heusler compounds Sc2MnZ(Z=C,Si,Ge and Sn) [J].Intermetallics,2014,46(34):243-249.

[23] Kandpal H C,Fecher G H,Felser C.Calculated electronic and magnetic properties of the half-metallic,transition metal based Heusler compounds [J].Journal of Physics D:Applied Physics,2007,40(6):1507-1523.
[24] Graf T,Casper F,Winterlik J,et al.Crystal structure of new Heusler compounds [J].Zeitschrift Fur Anorganische Und Allgemeine Chemie,2009,635(6/7):976-981.
[25] Kresse G,Furthmüller J.Efficient iterative schemes for ab initio total energy calculations using a plane-wave basis set [J].Physical Review B,1996,54(16):11169-11186.
[26] Perdew J P,Burke K,Ernzerhof M.Generalized gradient approximation made simple [J].Physical Review Letters,1996,77(18):3865-3868.
[27] Murnaghan F D.The compressibility of media under extreme pressures [J].Proceedings of the National Academy of Sciences of the United States of America,1944,30(9):244-249.
[28] Hirohata A,Kurebayashi H,Okamura S,et al.Structural and magnetic properties of epitaxial L21-structured Co2(Cr,Fe)Al films grown on GaAs(001) substrates [J].Journal of Applied Physics,2005,97(10):103714-103719.
[29] Xie J,Dong J,Lu J,et al.Epitaxial growth of ferromagnetic Ni2MnIn on(001) InAs [J].Applied Physics Letters,2001,79(7):1003-1005.
[30] Galanakis I,Dederichs P H,Papanikolaou N.Slater-Pauling behavior and origin of the half-metallicity of the full Heusler alloys [J].Physical Review B,2002,66(17):174429.
[31] Sakuraba Y,Hattori M,Oogane M,et al.Giant tunneling magnetoresistance in Co2MnSi/Al-O/Co2MnSi magnetic tunnel junctions [J].Applied Physics Letters,2006,88(19):192508-192513.

