Cu-Pt和Pd-Pt二元合金系中fcc相扩散迁移率参数的优化与计算
王翠萍,张炎财,卢 勇,蔺金燕,余 涌,刘兴军
(厦门大学材料学院,福建 厦门 361005)
Cu-Pt和Pd-Pt二元合金具有良好的导电率、高温抗氧化性、化学稳定性和焊接性能[1-5].大多数合金的物理性能和机械性能都与扩散行为有着密切的关系,因此,扩散过程的研究对新材料的开发具有重要的指导意义[6].如,用作氧气传感器的Pd-Pt多孔薄膜材料是通过Pd/Pt双层薄膜互扩散而得到的[4];Pd在Cu中的扩散会导致Cu-Pt薄膜表面的电阻明显增加[2].因此,有必要对Cu-Pt和Pd-Pt二元合金系中fcc相的扩散迁移率参数进行优化与计算,同时有关Cu-Pt和Pd-Pt基础二元合金系扩散的研究可以为Pt基多元合金系扩散的研究提供理论信息.
近年来,扩散的计算模拟是相变研究的一个重要发展方向.DICTRA (diffusion controlled transformation) 软件包是其中一个有效的模拟工具,它在CALPHAD (calculation of phase diagram)框架下进行操作,是CALPHAD方法的扩展[7-11].在扩散实验数据的基础上,结合体系的热力学描述,用DICTRA软件优化与计算体系的扩散迁移率参数.近年来,本课题组在建立材料热力学数据库研究的基础上,进一步开展了材料动力学方面的研究[12-15],并建立动力学数据库,为新材料的开发提供理论依据.
本研究是在扩散实验数据的基础上,结合体系的热力学描述,用DICTRA软件优化Cu-Pt和Pd-Pt二元合金系中fcc相的扩散迁移率参数,进一步完善Pt基合金的扩散迁移率数据库.同时,通过模拟扩散偶的浓度曲线进一步验证所获得的原子迁移率的准确性和有效性.
1 实验与计算信息
1.1 Cu-Pt二元合金系
Mishra等[16]利用EPMA方法,实验测定了在1 273 K时Cu/Pt扩散偶的浓度曲线.结合实验测定的扩散偶浓度曲线,同时采用Wagner[17]的关系式,Mishra等[16]计算了Cu-Pt二元合金系中fcc相在1 198~1 273 K温度范围内的互扩散系数,最后利用外推法将互扩散系数外推至0%(原子分数)Cu,从而获得1 198~1 273 K温度范围内的Cu在fcc-Pt中的杂质扩散系数.
Johnson等[18]通过实验测定了1 372~1 651 K温度范围内的Cu在fcc-Pt中的杂质扩散系数.
Kubaschewski等[19]通过实验测定了1 311~1 673 K温度范围内的Cu在fcc-Pt中的杂质扩散系数,并研究了Pt-13.9%(原子分数)Cu合金在1 311~1 673 K温度范围内的互扩散系数.
Matano[20]研究了Cu/Cu(7%~10%(质量分数)Pt)扩散偶,假设互扩散系数与浓度无关,用误差函数计算了Cu-Pt二元合金系中fcc相763~1 233 K温度范围内的互扩散系数.Matano[20]假设互扩散系数与浓度无关,但是这与Mishra等[16]报道的互扩散系数随浓度显著变化的情况完全相反,并且Matano[20]研究报道的实验数据与Mishra等[16]和Kubaschewski等[19]报道的实验数据都相差较大.故本研究在计算时没有采用Matano[20]报道的实验数据.
Liu等[21]利用CALPHAD方法,对Cu-Pt二元合金系中Pt的自扩散参数、杂质扩散参数和二元互扩散参数进行了优化与计算.但是关于Cu在fcc-Pt中杂质扩散的实验数据有新的文献报道;以及Liu等[21]优化二元互扩散参数所采用的实验信息[19-20]很有限,而且计算结果和实验数据[20]相差较大,也没有考虑有关扩散偶方面的研究信息.所以本研究在综合考虑有关Cu-Pt二元合金系的实验信息[16,18-19]的基础上,对Cu-Pt二元合金系中fcc相的Cu在fcc-Pt中的杂质扩散与Cu-Pt二元合金系的互扩散迁移率参数进行重新优化与计算.
1.2 Pd-Pt二元合金系
Baheti等[6]利用EPMA方法,实验测定了在1 573 K时Pd/Pt扩散偶的浓度曲线.结合实验测定的扩散偶浓度曲线,同时采用Wagner[17]的关系式,Baheti等[6]计算了Pd-Pt二元合金系中fcc相1 423~1 573 K温度范围内的互扩散系数,最后利用外推法将互扩散系数外推至0和100%(原子分数)Pt,从而获得Pt在fcc-Pd和Pd在fcc-Pt中的杂质扩散系数.
Yelokhina等[22]利用X射线光谱分析方法,通过对比试样和标样的同种类型的X射线光谱强度来确定组元的成分,从而获得扩散偶浓度曲线.通过Matano-Boltzmann方法计算了Pd-Pt二元合金系中fcc相在1 340~1 685 K温度范围内的互扩散系数.但是Yelokhina等[22]报道的与Baheti等[6]报道的互扩散系数随浓度的变化趋势相差很大.
到目前为止,关于Pd-Pt二元合金系中fcc相的扩散迁移率参数的优化与计算还未见研究报道.因此本研究基于Baheti等[6]报道的最新实验数据,对Pd-Pt二元合金系中fcc相的扩散迁移率参数进行优化与计算.
2 模型描述
根据菲克第一定律,扩散组元k的时空演化可以表示为:
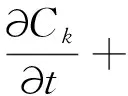
(1)
其中Ck为组元k的浓度,t为扩散时间.当组元i以摩尔分数表示时,多组元系统中组元i的扩散通量Jk可定义为:

(2)


(3)
其中δik是Kronecker符号(如果i=k则δik=1,否则δik=0),xi是摩尔分数,μi是元素i的化学势,Mi是与成分有关的原子迁移率参数.

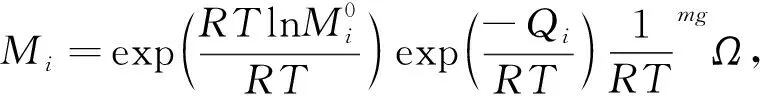
(4)

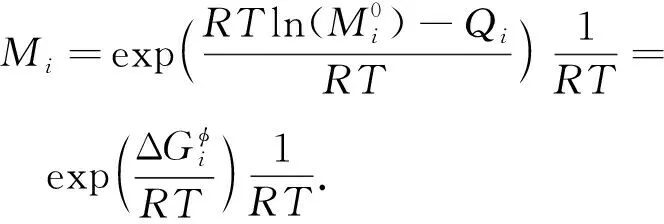
(5)


(6)
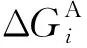
3 结果与讨论
3.1 Cu-Pt二元合金系
扩散迁移率参数的优化与计算需要对体系各相进行准确的热力学描述.Abe等[27]采用CALPHAD方法,对Cu-Pt二元合金系的相图进行了热力学优化与计算,计算的Cu-Pt二元合金系的相图如图1所示.本研究利用Abe等[27]优化的热力学参数及DICTRA软件的Parrot模块,对Cu-Pt二元合金系扩散迁移率参数进行了优化,其原理是利用最小二乘法来拟合实验数据.Cu和Pt在fcc相中的自扩散系数分别采用了Wang等[28]和Liu等[21]的研究结果,Pt在fcc-Cu中的杂质扩散系数利用了Liu等[21]的研究结果.本研究在Johnson等[18]和Kubaschewski等[19]报道的Cu在fcc-Pt中的杂质扩散实验数据基础上,结合Mishra等[16]报道的最新实验数据,对Cu在fcc-Pt中的扩散迁移率参数重新进行了优化与计算.基于Mishra等[16]和Kubaschewski等[19]报道的实验数据,对Cu-Pt二元合金系的互扩散迁移率参数进行了优化和计算,所获得的具体参数如表1所示.

图3 计算的Cu-Pt合金中fcc相的互扩散系数与成分(a)、温度(b,c)间的关系曲线Fig.3 Calculated concentration (a),temperature (b,c) dependence of inter-diffusion coefficients in Cu-Pt fcc alloys
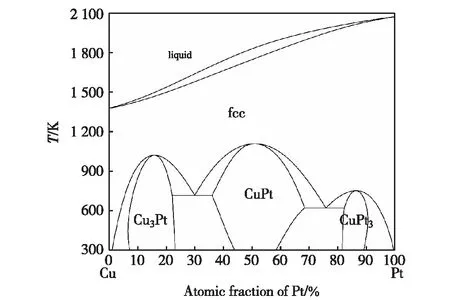
图1 Abe等[27]计算的Cu-Pt二元系相图Fig.1 The phase diagram of the Cu-Pt system calculated by Abe et al[27]
本研究计算的Cu在fcc-Pt中的杂质扩散系数与温度的变化关系如图2所示.从图2中可以看出,计算结果和实验结果[16,18-19]符合良好.
图3(a)是计算的在不同温度下,Cu-Pt二元合金系的互扩散系数与Cu浓度的关系曲线,从图可见,计算结果和Mishra等[16]报道的实验数据取得了较好的一致性.图3(b)是计算的Cu-Pt部分合金的互扩散系数与温度之间的关系曲线,从图可以看出,计算结果与实验数据[16]符合良好,但是与Kubaschewski等[19]测定的实验数据在高温处略有差别,但是总体来看,计算结果还是在可以接受的范围内.图3(c)是局部放大计算的Pt-10%Cu、Pt-20%Cu、Pt-30%Cu和Pt-40%Cu合金(其中的百分数均为原子分数)的互扩散系数与温度之间的关系曲线,如图所示,计算结果与实验数据[16]取得了良好的一致性.

表1 Cu-Pt二元合金系中fcc相的扩散迁移率参数Tab.1 Diffusion mobility parameters of Cu-Pt fcc alloys
注:ΔG单位为kJ/mol,T单位K,下同.
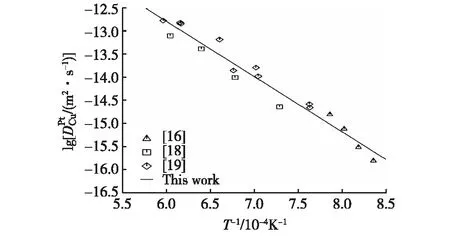
图2 计算的Cu在fcc-Pt中的杂质扩散系数Fig.2 Calculated impurity diffusion coefficients of Cu in fcc-Pt
为了进一步验证本研究所优化的扩散迁移率参数的准确性,利用表1中的动力学参数,对在1 273 K时退火处理32 400 s的Cu/Pt扩散偶浓度曲线进行了计算.计算结果和实验值的比较如图4所示.计算值和实验值[16]符合得很好,这进一步验证了所优化的Cu-Pt二元合金系扩散迁移率参数的准确性.
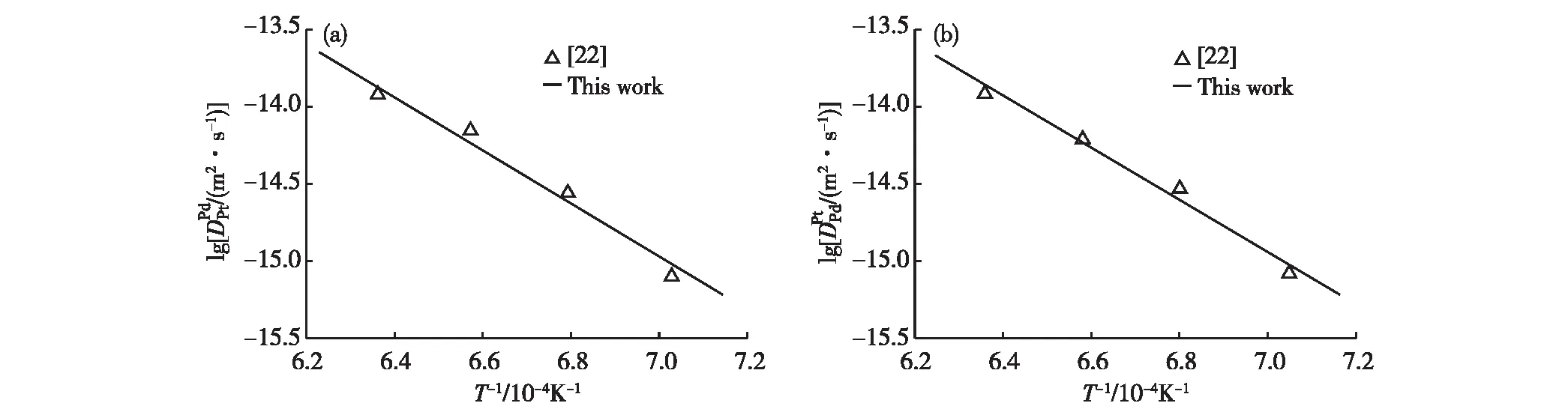
图6 计算的Pt在fcc-Pd(a)和Pd在fcc-Pt(b)中的杂质扩散系数Fig.6 Calculated impurity diffusion coefficients of Pt in fcc-Pd (a) and Pd in fcc-Pt (b)

图4 计算的Cu/Pt扩散偶在1 273 K下 退火32 400 s的浓度曲线Fig.4 Calculated concentration profile for Cu/Pt diffusion couple annealed at 1 273 K for 32 400 s
3.2 Pd-Pt二元合金系
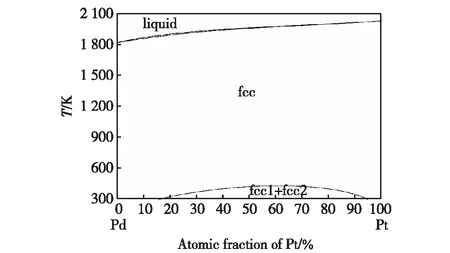
图5 Okamoto[29]计算的Pd-Pt二元系相图Fig.5 The phase diagram of the Pd-Pt system calculated by Okamoto[29]
Okamoto[29]采用CALPHAD方法,对Pd-Pt二元合金系的相图进行了热力学优化与计算,计算的Pd-Pt二元系相图如图5所示.本研究利用Okamoto[29]优化的热力学参数及DICTRA软件的Parrot模块,对Pd-Pt二元合金系扩散迁移率参数进行了优化.Pd在fcc相中的自扩散系数采用了Liu等[30]的研究结果.本研究基于Baheti等[6]报道的实验数据优化与计算了Pd-Pt二元合金系中Pt在fcc-Pd与Pd在fcc-Pt中的杂质扩散迁移率参数和二元互扩散迁移率参数,其具体参数如表2所示.
图6(a)和(b)是计算的Pt在fcc-Pd和Pd在fcc-Pt中的杂质扩散系数,如图所示,计算结果和Baheti等[6]报道的实验结果取得了较好的一致性.

表2 Pd-Pt二元合金系中fcc相的扩散迁移率参数Tab.2 Diffusion mobility parameters of Pd-Pt fcc alloys

图7 计算的Pd-Pt二元合金系中fcc相的互扩散系数与成分(a)、温度(b)之间的关系曲线Fig.7 Calculated concentration(a), temperature (b) dependence of inter-diffusion coefficients in Pd-Pt fcc alloys
本研究计算了在不同温度下,Pd-Pt二元合金系的互扩散系数与Pt浓度之间的关系曲线,如图7(a)所示,计算的互扩散系数与Baheti等[6]报道的实验数据符合良好.图7(b)是计算的Pd-3.5%Pt和Pd-50% Pt合金(其中的百分数均为原子分数)的互扩散系数与温度之间的关系曲线,如图所示,计算结果与实验结果[6]取得了良好的一致性.
本研究利用表2中的动力学参数,计算模拟了在1 573 K温度下,退火处理90 000 s的Pd/Pt扩散偶浓度曲线,如图8所示.从图8中可以看出,模拟结果与Baheti等[6]报道的实验数据符合良好,这进一步验证了所优化的Pd-Pt二元合金系扩散迁移率参数的准确性.
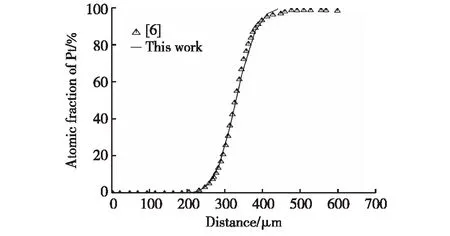
图8 计算的Pd/Pt扩散偶在1 573 K下 退火90 000 s的浓度曲线Fig.8 Calculated concentration profile for Pd/Pt diffusion couple annealed at 1 573 K for 90 000 s
4 结 论
基于Cu-Pt和Pd-Pt二元合金系的扩散实验数据,本研究采用DICTRA软件分别对Cu-Pt和Pd-Pt二元合金系中fcc相的扩散迁移率参数进行了优化与计算,计算结果和实验数据取得了良好的一致性.同时利用优化的扩散迁移率参数计算模拟了扩散偶浓度曲线,其模拟结果与实验数据符合良好,进一步验证了优化的扩散迁移率参数的准确性和有效性.
[1] Sausa R C,Gupta A.Laser decomposition of platinum metallo-organic films for electroless copper plating [J].J Electrochem Soc,1987,134(11):2707-2713.
[2] Shih D Y,Chang C A,Paraszczak J,et al.Thin-film interdiffusions in Cu/Pd,Cu/Pt,Cu/Ni,Cu/NiB,Cu/Co,Cu/Cr,Cu/Ti,and Cu/TiN bilayer films:correlations of sheet resistance with Rutherford backscattering spectrometries [J].J Appl Phys,1991,70(6):3052-3060.
[3] Zhang J Y,Boyd I W.Excimer lamp-induced decomposition of platinum acetylacetonate films for electroless copper plating [J].Solid-State Electronics,1999,43(6):1107-1111.
[4] Nazarpour S,Chaker M.Fabrication of porous Pt-Pd electrodes using solid state interdiffusion [J].Thin Solid Films,2012,520(14):4812-4815.
[5] Moysan I,Paul-Boncour V,Thiebaut S,et al.Pd-Pt alloys:correlation between electronic structure and hydrogenation properties [J].J Alloy Compd,2001,322(1):14-20.
[6] Baheti V A,Ravi R,Paul A.Interdiffusion study in the Pd-Pt system [J].J Mater Sci:Mater Electron,2013,24(8):2833-2838.
[7] Andersson J O,Höglund L,Jönsson B,et al.Fundamentals and applications of ternary diffusion [J].New York:Pergamon Press,1990:153-163.
[8] Andersson J O,Ågren J.Models for numerical treatment of multicomponent diffusion in simple phases [J].J Appl Phys,1992,72(4):1350-1355.
[9] Borgenstam A,Engström A,Höglund L,et al.DICTRA,a tool for simulation of diffusional transformations in alloys [J].J Phase Equilib,2000,21(3):269-280.
[10] Kaufman L,Bernstein H.Computer calculation of phase diagrams [M].New York:Academic Press,1970.
[11] Sundman B,Jansson B,Andersson J O.The thermo-calc databank system [J].CALPHAD,1985,9(2):153-190.
[12] Wang C P,Yan L N,Han J J.Diffusion mobilities in the fcc Ag-Cu and Ag-Pd alloys [J].CALPHAD,2012,37:57-64.
[13] Liu X J,Hu H H,Han J J,et al.Assessment of the diffusional mobilities in fcc Ni-Nb and fcc Ni-Mo alloys [J].CALPHAD,2012,38:140-145.
[14] Wang C P,Zhuang C P,Han J J,et al.Assessment of the atomic mobilities for binary Al-Ag fcc alloys [J].CALPHAD,2012,37:145-150.
[15] Wang C P,Yan L N,Han J J,et al.Diffusion mobilities in the fcc Ag-Cu and Ag-Pd alloys [J].CALPHAD,2012,37:57-64.
[16] Mishra B,Kiruthika P,Paul A.Interdiffusion in the Cu-Pt system [J].J Mater Sci:Mater Electron,2014,25(4):1778-1782.
[17] Wagner C.The evaluation of data obtained with diffusion couples of binary single-phase and multiphase systems [J].Acta Met,1969,17(2):99-107.
[18] Johnson R D,Faulkenberry B H.Diffusion coefficients of copper and platinum into copper-platinum alloys[M].[S.l.]:Air Force Materials Laboratory,Aeronautical Systems Division,Air Force Systems Command,1963.
[19] Kubaschewski O,Ebert H.Diffusion measurements in gold and platinum alloys [J].Z Elektrochem,1944,50:138-144.
[20] Matano C.X-ray studies on the diffusion of metals in copper [J].Jpn J Phys,1934,9(2):41-47.
[21] Liu Y,Zhang L,Yu D.Diffusion mobilities in fcc Cu-Au and fcc Cu-Pt alloys[J].J Ph Equilib Diff,2009,30(2):136-145.
[22] Yelokhina L V,Shalaev V I.Mutual diffusion in palladium-platinum alloys[J].Fiz Met Metalloved,1987,63(5):958-964.
[23] Jönsson B.Ferromagnetic ordering and diffusion of carbon and nitrogen in bcc Cr-Fe-Ni alloys [J].Z Metallkd,1994,85(7):498-501.
[24] Jönsson B.Assessment of the mobility of carbon in fcc C-Cr-Fe-Ni alloys [J].Z Metallkd,1994,85(7):502-509.
[25] Jönsson B.On ferromagnetic ordering and lattice diffusion:a simple model [J].Z Metallkd,1992,83(5):349-355.
[26] Redlich O,Kister A T.Thermodynamics of nonelectrolyte solutions-x-y-trelations in a binary system [J].Ind Eng Chem,1948,40(2):341-345.
[27] Abe T,Sundman B,Onodera H.Thermodynamic assessment of the Cu-Pt system [J].J Phase Equilib Diff,2006,27(1):5-13.
[28] Wang J,Liu H S,Liu L B,et al.Assessment of diffusion mobilities in fcc Cu-Ni alloys [J].CALPHAD,2008,32(1):94-100.
[29] Okamoto H.Pd-Pt (palladium-platinum) [J].J Phase Equilib,1991,12(5):617-618.
[30] Liu Y J,Liang D,Du Y,et al.Mobilities and diffusivities in fcc Co-X (X=Ag,Au,Cu,Pd and Pt) alloys [J].CALPHAD,2009,33(4):695-703.

