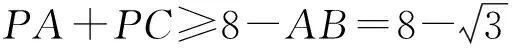异侧和最小 同侧差最大
——到两定点距离之和与差的最值问题的新观察
●
(海头高级中学 江苏赣榆 222111)
1 问题提出
解析几何中,我们常遇到1个动点到2个定点距离之和与差的最值问题,此类问题的条件通常是给出2个定点和1个动点,动点往往有固定的轨道,所求的问题一般是动点到2个定点的距离之和或差.此类问题往往因为定点处于轨道的异侧与同侧之分,轨道也有直线与曲线之别,距离又分和差,最值有最大也有最小,所以看起来解法各异,甚是灵活.不少学生遇到这些问题,往往都是不同问题应用不同方法,一题一议,一题一法.然而笔者在教学实践中却意外发现,它们的处理方式虽形式各异,但本质上都可以转化为初中学生都明白的2个简单的数学模型.
2 2个经典的最值应用模型
“两点之间,线段最短”,简单的8个字蕴涵着生活的哲理,它是我们都熟悉的一个“距离公理”,它的应用也非常广泛.大家最熟悉的一个例子:张庄和李庄是位于公路2旁的2个村庄,若要在公路上建一个汽车站,欲使2个村庄到该车站的距离之和最小,试设计出车站的最佳位置,并说明理由.这是该数学公理最简单也是最典型的实例,影响深远,由此可以抽象出如下的数学模型:
模型1
如图1,已知点A,B在直线l的异侧,在l上求一点M,使得MA+MB最小.
分析
根据两点之间,线段最短,联结AB,与直线l的交点是M′便是要求的点M.
证明
在直线l上任取一点M,得MA+MB≥AB,当且仅当点M与M′重合时有M′A+M′B=AB,因此MA+MB的最小值是AB的长度.
上面这个模型最典型的特征是:(1)定点A,B位于动点运动轨道的异侧;(2)可求距离之和的最小值.简单地说,就是“异侧和最小”
上述最值的证明所采用的原理是“两点之间,线段最短”,但事实上也可以理解为“三角形两边之和大于第三边”.从这一角度看,既然“三角形两边之和大于第三边”,那么同时也应该有“三角形两边之差小于第三边”所对应的最值问题存在,也就是说上述模型可以改编为求距离之差的问题,由此可以得到下面的新数学模型:

图1 图2
模型2
如图2,已知点A,B在直线l的同侧,在l上求一点M,使得MA-MB最大.
分析
延长AB交直线l于点M′,如图2,线段AB与直线l的交点是M′便是要求的点M.
证明
在直线l上任取一点M,得MA-MB≤AB,当且仅当点M与M′重合时有M′A-M′B=AB,因此MA-MB的最大值是AB的长度.
上面这个模型典型特征是:(1)定点A,B位于动点运动轨道的同侧;(2)可求距离之差的最大值.简单地说,就是“同侧差最大”.
3 对2个经典最值应用模型的解题体验与规律探究
3.1 定点在动点轨迹的位置可以相互转换
例1
[1]已知点A(-3,8),B(2,2),点P是x轴上的点,求PA+PB的最小值.

图3
解
如图3,在x轴上任取一点P,作B(2,2)关于x轴的对称点B1(2,-2),则PB=PB1.联结PB1,PA,PB,联结AB1交x轴于点P1,则PA+PB=PA+PB1≥AB1,也就是说点P移动到与点P1重合时,取到最小值

评注
本题中的2个定点在x轴的同侧,这和模型1中“定点位于动点轨迹的异侧”的条件不相符,不在异侧,2个定点与1个动点无法在一条直线上,也就无法直接利用“两点之间,线段最短”,但是利用对称将同侧的点转化为异侧的点,从而划归成模型1求解,确保“异侧和最小”.
变式1

解
原式可化为
相当于已知点A(-3,8),B(2,2),点P是x轴上的点,求PA-PB最大值.延长AB交x轴于点P′,则PA-PB≤AB,也就是说点P移动到与点P′重合时,取到最大值

评注
不少学生在配方转化时常有困惑,即定点A,B坐标的符号不好把控,比如有人怀疑定点要是误写成B(2,-2),还和原来的结果一样吗?答案是肯定的.因为虽不满足“同侧差最大”,但是完全可以通过对称把它们拉到“同侧”.
3.2 动点运动的轨道可以是直线也可以是曲线
例2
已知点P是抛物线y2=4x上的动点,F(1,0),A(4,5),则PA+PF的最小值是______.
解


图4 图5
评注
本题和例1一样,也是求动点P到2个定点距离之和的最小值问题,利用原理一致,和模型1极其相似.不同的是这里的动点运动轨道不是直线而是抛物线,但这并不影响我们利用“距离公理”求最值.可见动点的轨迹不一定局限于直线,还可以是抛物线、双曲线、椭圆,甚至是一般函数图像.
3.3 定点在动点运动轨迹的同侧与异侧也是相对的
例3
已知点P是函数f(x)=x3-3x上的动点,A(-2,-2),B(1,2),则PA+PB的最小值是______.
解
令f′(x)=3x2-3=0,得x=±1.若f′(x)>0,则x>1或x<-1;若f′(x)<0,则-1 PA+PB≥AB=P1A+P1B= 评注 本题把点A,B之间的部分曲线看成动点轨迹,由本题2个定点A,B可以看成位于轨迹异侧的2个点,符合“异侧和最小”的特征,因此可以直接求PA+PB的最小值. 变式2 已知点P是函数f(x)=x3-3x上的动点,A(-2,-2),B(1,2),若PA>PB,则PA-PB的最大值是______. 解 (同上)如图6.联结AB,延长交f(x)的图像于点P2,则 PA-PB≤AB=P2A-P2B= 评注 本题定点A,B并没有变动,轨迹也没有改变,但是动点在曲线上的位置可以自由移动.如果我们把点B右侧的部分曲线看成是点P的运动轨迹,那么AB就变成了轨迹同侧的2个点,符合“同侧差最大”特点,可直接求PA-PB的最大值. 图6 图7 例4 已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,点M,N分别是圆C1,C2上的动点,P为x轴上的动点,则PM+PN的最小值为______. 解 假设点P位置如图7所示,则 PMmin=PC1-1,PNmin=PC2-3, PM+PN≥PC1+PC2+4. 取C1(2,3)关于x轴的对称点C1′(2,-3),当且仅当点C1′,P,C2共线,距离之和最小,此时 PM+PN≥PC1+PC2-4= PC1′+PC2-4≥ 评注 本题条件中不见2个定点,但是当我们把动点暂时看作定点时,转化为圆外一点到圆上点的距离PM与PN的最小值,从而获得轨迹同侧的2个定点C1与C2,并最终转化为x轴上的动点到x轴异侧的2个定点距离之和的最小值问题. 例5 已知点P是抛物线y2=4x上的动点,F(1,0),A(4,3),则PA-PF的最大值和最小值是______. 解 如图8,可判断点A,F都在抛物线的内侧,直线AF与抛物线相交于2个点P1,P2,当PA≥PF时,根据“三角形两边之差小于第三边”,得PA-PF≤FA,而FA=P1A-P2F可以取到,于是 图8 图9 评注 一般地,若动点P在直线上,2个定点A,B位于直线的同侧,可以求PA-PF的最大值而不能求最小值,即“同侧差最大”.但是动点P在曲线上,为什么就可以求PA-PF的最大值和最小值呢?看了上面的曲线大家可能就明白了,这就是因为在延长线段AF的时候,与曲线可以有2个甚至更多的交点,而直线与直线最多只能有1个交点. 例6 已知B地在A地的正东方向4 km处,C地在B地的北偏东30°方向2 km处,河流的没岸PQ(曲线)上任意一点到A的距离比到B的距离远2 km.现要在曲线PQ上选一处M建一座码头,向B地和C地转运货物.经测算,从M到B,M到C修建公路的费用是每千米a万元,那么修建这2条公路的总费用最低是______万元. 解 Q=a·MB+a·MC=Q=a·(MB+MC)= a·(MA-2a+MC), 从而 评注 本题要求MA+MC最小值,本来定点在曲线同侧,怎么求最小值呢?要么把“和”改为“差”,要么把“同侧”改为“异侧”.本题利用双曲线的定义,把“同侧”改为“异侧”,问题就符合“异侧和最小”的特征了. 变式3 解 如图10,过点B作左准线的垂线,垂足为M.过点A作此准线的垂线,在x轴上的垂足为M′.根据椭圆的第二定义得 评注 图10 图11 例7 解 根据椭圆的定义,PB+PC=2a=8,从而 PA+PC=PA+(8-PB)=8-(PB-PA). 为使PA+PC取得最小值,只需PB-PA取得最大值,此时只有点A,B,P共线时才可以取得,这时 评注当定点在轨迹的同侧时,一般更适合于求PA-PC的最大值.而求PA+PC的最小值,通常是定点位于轨迹的异侧,于是借助第一定义改变定点的位置,最终2个定点虽然谁也没有越过轨迹到达异侧,却有意外收获.即本来要求PA+PC的最小值,却变成了求PB-PA的最大值,这也正好符合“同侧差最大”的要求. 综上所述,解析几何中求动点到2个点距离的和(差)的最值,是最常见的一类最值问题.其解题策略多种多样,但是本质上却可以划归成距离最值的简单应用模型.把2个数学模型研究透了,掌握定点与轨迹的位置关系,理清求最大值与最小值的基本规律,依据“异侧和最小,同侧差最大”的基本原理,便可以以不变应万变,以逸待劳,乐享其中. 参 考 文 献 [1] 薛胜菊,赵洋.与图形有关的最值问题[J].教学考试(数学),2013(11):63-70.


3.4 动中求静,化动为定
4 圆锥曲线中的几个最值问题的再认识
4.1 对于PA-PF,既可以求最大值也可以求最小值


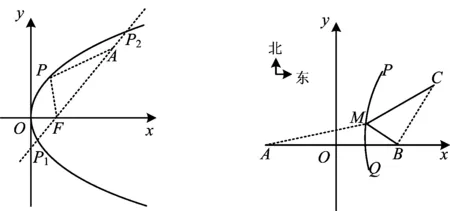
4.2 “求和”变不成“求差”,可改“同侧”为“异侧”



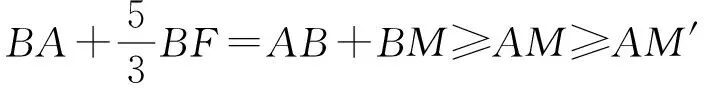



4.3 “同侧”不能变“异侧”,改“和”为“差”