基于蒙特卡罗-离散纵标双向耦合方法的堆坑粒子注量率计算

韩静茹，陈义学，袁龙军，张春明

(1.华北电力大学 核科学与工程学院，北京 102206；2.环境保护部 核与辐射安全中心，北京 100082)

在核电站设计中，反应堆压力容器位于反应堆堆坑内，压力容器和一次混凝土屏蔽墙之间构成的空间一般称为堆腔。反应堆运行过程中，堆芯中的一部分中子和光子从压力容器外表面逸出，进入堆腔，并继续向外泄漏，有一部分泄漏到压力容器下方的堆坑底部。堆坑底部设有堆坑通道、小室及堆内测量仪表间，用于压力容器绝热层、压力容器监测设备及堆内测量仪表的安装和维修。堆坑粒子注量率计算分析对于核电站设计和安全分析具有重要意义。

堆坑底部粒子注量率计算涉及的横向、纵向尺寸均达十多米，且中间的屏蔽构件几何复杂，显然这是一大尺寸复杂几何系统内的输运问题。由于反应堆厂房几何尺寸较大，且堆坑通道轴线与反应堆主轴垂直，则自压力容器外表面泄漏的粒子到达小室屏蔽门附近的几率很小。直接采用单一的蒙特卡罗(MC)方法难以在有效的时间内解决此类小概率事件问题。而在压力容器外，由于主冷却剂进、出口接管，堆外探测器孔道，堆坑通道及小室等的存在，堆腔几何结构极为复杂，单一的离散纵标(SN)法难以精确描述堆坑及小室的复杂几何，使计算结果产生较大误差。因此，本文提出结合两种方法优势的三维蒙特卡罗-离散纵标双向耦合(MC-SN双向耦合)方法，用于压水堆堆坑底部辐射泄漏粒子注量率的计算。

1 MC-SN双向耦合方法

MC和SN方法是求解中子输运问题的两种不同方法。MC方法通过对大量单个粒子的运动历史逐个进行跟踪模拟，然后用统计方法给出随机变量某个特征的估计量，作为问题的解，SN方法是在相空间(r×E×Ω)内对空间r、能量E和方向变量Ω采用直接离散方法数值求解中子输运方程，得到网格ri、能群Eg和离散方向Ωm区间内的粒子角通量密度ψ(ri,Eg,Ωm)。实现蒙特卡罗方法和离散纵标方法之间的耦合计算，关键在于MC模拟的粒子径迹信息与SN方法计算的角通量密度之间的相互转换。其中，MC粒子径迹信息到SN角通量密度的转换关系[1]如下：

(1)

式中：ψi,j,k,m,g为空间网格(i,j,k)中第g能群内m方向范围内的粒子角通量密度；weightn为MC粒子n的权重；wm为求积权重系数；N为MC模拟的源粒子数；ΔA为给定面元的面积；λn为MC粒子径迹和面法线方向夹角的余弦值；En、rn和Ωn分别为粒子的能量、空间位置和飞行方向。

SN角通量密度到MC粒子径迹信息的转换关系[2]如下：

(2)

(3)

(4)

式中：λm为粒子飞行方向与面法线方向夹角的余弦值；Ai为网格区间ri对应的连接面的面积；I、G和M分别为连接面网格数、能群数和离散方向数；p(ri)为MC抽样粒子位于网格区间ri内的概率；p(Eg/ri)为在网格区间ri内抽样，粒子位于能群区间Eg内的概率；p(Ωm/Eg/ri)为在网格区间ri、能群区间Eg内抽样，粒子位于离散方向Ωm内的概率。

2 MC-SN双向耦合系统框架

基于蒙特卡罗-离散纵标法的双向耦合计算框架如图1所示。根据MC-SN双向耦合转换方法，通过自主研发接口程序来实现。三维MC-SN双向耦合系统流程如图2所示，其中MC程序采用国际通用的粒子输运程序MCNP[3]；SN程序采用美国橡树岭国家实验室开发的三维离散纵标程序TORT[4]。在耦合系统中，为了充分发挥两种方法的优势，MCNP和TORT分别用以模拟复杂几何区和大块屏蔽区的计算。其中MCNP计算得到的穿过指定面的粒子数据被精确记录在SSW面源文件中，通过MC-SN接口程序用于生成TORT程序的边界源文件，作为TORT程序的输入之一，实现三维MC和SN耦合输运计算；TORT计算得到连接面的粒子角通量密度，SN-MC接口程序将连接面的角通量密度转换为粒子概率分布，再经MC-SOURCE源粒子抽样程序转换为MC源粒子信息参数，为MCNP计算提供源项，实现三维SN和MC耦合输运计算。

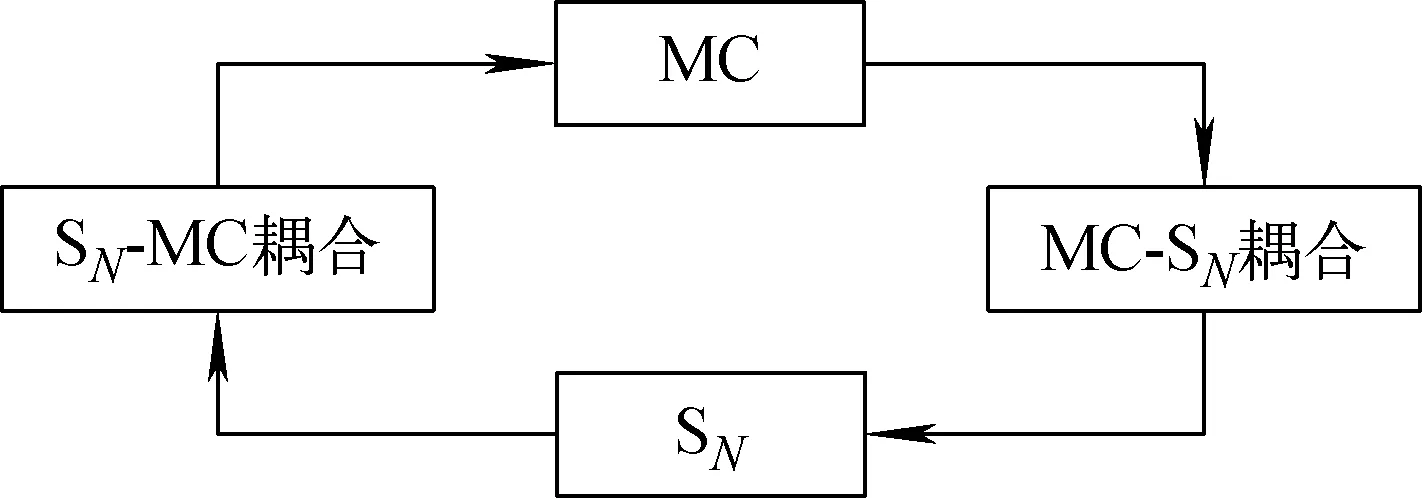
图1 MC-SN双向耦合系统框架

MC-SN双向耦合系统可处理三维x-y-z及R-θ-z几何。对于大尺寸复杂几何系统屏蔽计算问题，可选取MC-SN双向耦合方法，针对装置自身特点，设计较优的分割方案，灵活选择不同的耦合方法和程序进行屏蔽计算。既可提高对大型复杂核装置屏蔽问题计算结果的可靠性和精确度，同时又提高了收敛速度，节省了机时。

3 计算模型及步骤

3.1 计算模型

某反应堆及堆坑布置如图3所示。堆坑通道和小室相连通，布置在51°方位上，与反应堆主轴线相垂直。屏蔽门在小室侧部，通风孔布置在小室顶部[5]。根据计算模型特点，采用MC-SN-MC耦合程序系统对堆坑底部通道和小室进行中子、光子注量率分布计算，用以提供小室屏蔽门设计所需的辐照强度数据。

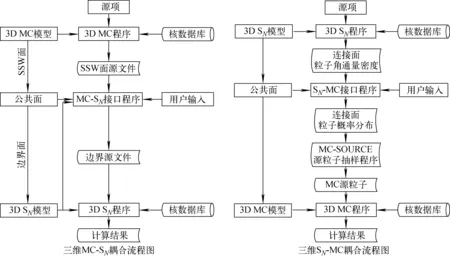
图2 三维MC-SN双向耦合系统流程图

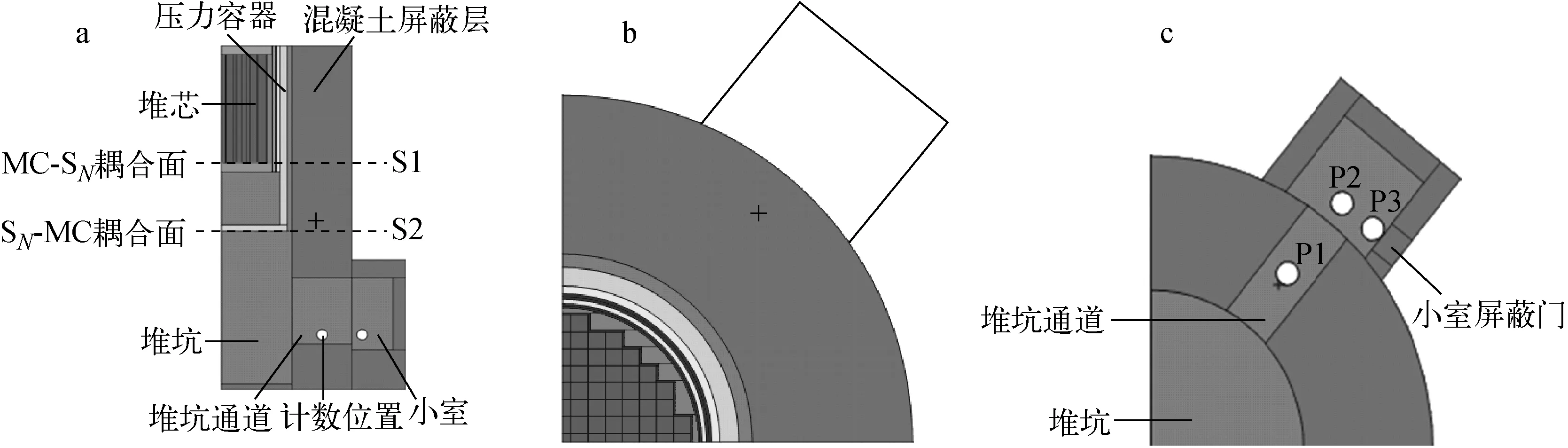
a——垂直剖面图；b——水平剖面图；c——堆坑底部及探测器示意图

本计算模型中，系统坐标原点设置在堆芯中平面处，坐标系z轴与反应堆轴心线重合，x轴和y轴分别与0°方位和90°方位重合。计算中设置了两个耦合面S1和S2(图3a)。位于堆芯下表面上的S1，其为高度z=-182.88 cm、半径为221.655 cm的90°圆平面，在此表面上实现MC-SN耦合计算；位于压力容器底面，高度z=-413.526 cm处，半径为221.655 cm的90°圆平面S2为第2耦合面，在此表面上实现SN-MC耦合。P1、P2和P3分别表示反应堆堆坑通道、小室及小室屏蔽门附近的探测器(图3c)，均为半径为18 cm的小球。表1列出3个探测器的具体坐标位置。

表1 反应堆堆坑探测器的位置

3.2 计算步骤

三维MC-SN-MC耦合计算具体步骤如下。1) MC计算：采用MCNP建立反应堆下反射层以上区域的精细模型进行计算，求得穿过S1表面的粒子(中子、光子)径迹信息，并存储到WSSA文件。2) MC-SN计算：采用MC-SN接口程序将WSSA文件中记录的粒子径迹信息转换为角通量密度分布，并生成SN边界源文件。3) SN计算：采用TORT建立S1表面到压力容器底面的R-θ-z模型，选取P3阶勒让德展开，S8全对称高斯求积组，进行边界源计算，得到S2面粒子角通量密度分布，完成三维MC-SN耦合计算。4) SN-MC计算：通过SN-MC接口程序，将TORT计算得到的S2面上的粒子角通量密度分布转换为中子在空间、能量和方向上的概率分布函数。5) MC计算：在压力容器底面S2以下，采用MCNP建立堆坑精细模型，通过已嵌入MCNP程序的源抽样程序MC-SOURCE对第4步中的概率分布函数进行抽样，跟踪模拟S2面上的粒子，计算求得堆坑底部3个探测器的中子和光子注量率分布，完成三维SN-MC耦合计算。耦合计算中MCNP计算采用点截面数据库，TORT计算采用包含30群中子和12群光子的TEXT10多群数据库。本计算中的模型结构尺寸及材料与实际反应堆存在一定差别，计算结果为1个中子源的归一化结果。

4 计算结果分析及讨论

4.1 MC-SN-MC耦合计算结果

采用三维MCNP-TORT-MCNP耦合程序，设置F4体探测器计数，计算得到3个探测器处的中子和光子注量率。同时根据NCRP-38[6]中的中子通量-剂量转换因子和光子通量-剂量转换因子求得指定探测器处的剂量率。耦合计算中，最耗时的为上节计算步骤中所描述的第1步和第5步中的MCNP程序计算过程。其中第1步MCNP计算300 min，S1面获得1.0×106个粒子径迹，第5步中MCNP中子光子输运计算分别进行，其中中子计算400 min，光子计算2 000 min，获得P1、P2和P3处中子和光子注量率分布。MC-SN-MC计算得到的3个探测器处归一化的中子注量率、中子剂量率、光子注量率及光子剂量率值列于表2。可看出：堆坑底部通道、小室及小室屏蔽门附近，对辐射剂量安全起主导作用的是中子，光子对剂量率的贡献较中子小1～2个数量级。

3个探测器处的中子能谱和光子能谱示于图4。可看出，P1、P2和P3处的粒子能谱分布趋势基本一致，小室屏蔽门附近P3探测器处的中子和光子注量率均为最低。

表2 堆坑底部探测器处粒子注量率和剂量率

注：括号内为统计误差

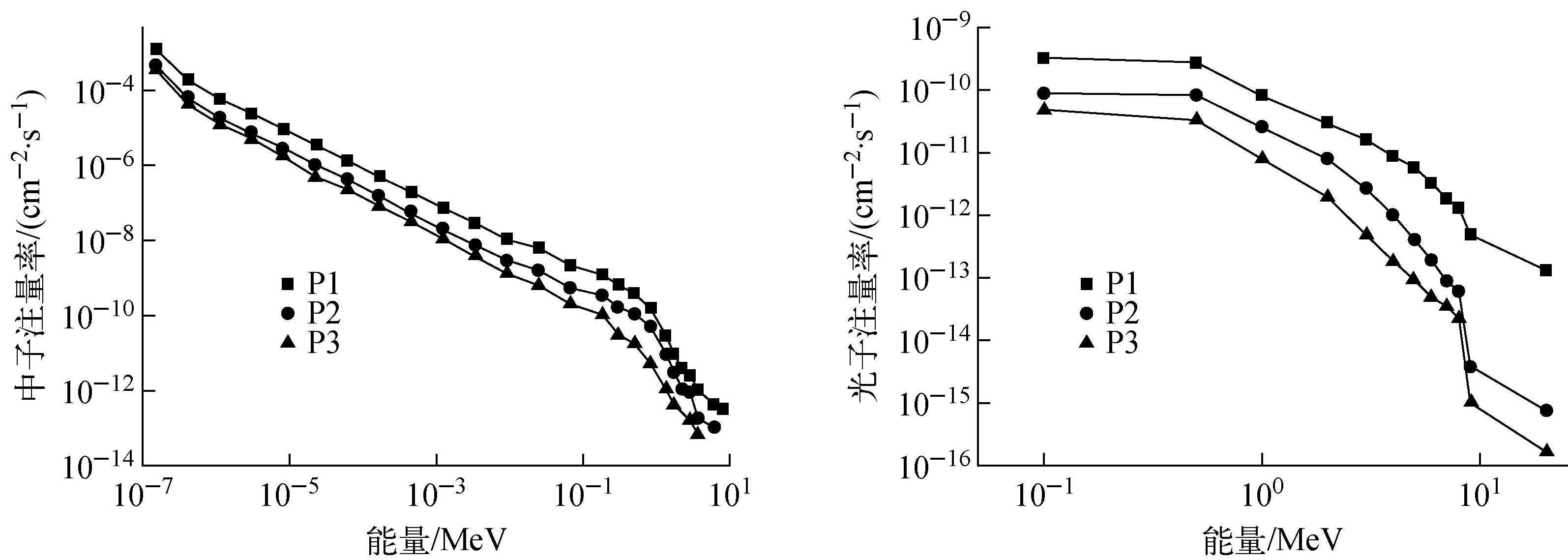
图4 探测器处中子能谱和光子能谱

4.2 计算结果验证比较

采用单一的MCNP程序建立整个模型，并采取相同的探测器计数，计算34 000 min后，跟踪模拟2.0×108个粒子，P1、P2和P3探测器处中子注量率的统计误差分别达到4.52%、7.78%和10.37%。由此可见，单一的蒙特卡罗方法在求解深穿透复杂屏蔽计算问题时很难收敛。选取单一的MCNP计算相对统计误差最小的P1探测器处的中子注量率分布与三维MCNP-TORT-MCNP计算结果比较，结果如图5所示，中子能谱分布趋势相同。耦合程序计算的P1处的中子注量率较MCNP的计算结果偏低约2.92%，主要是由于MCNP程序计算结果相比耦合计算统计误差相对偏大。单一MCNP程序随着计算时间的增加，结果呈变小趋势。初步证明了三维MC-SN双向耦合程序系统的正确性和有效性。

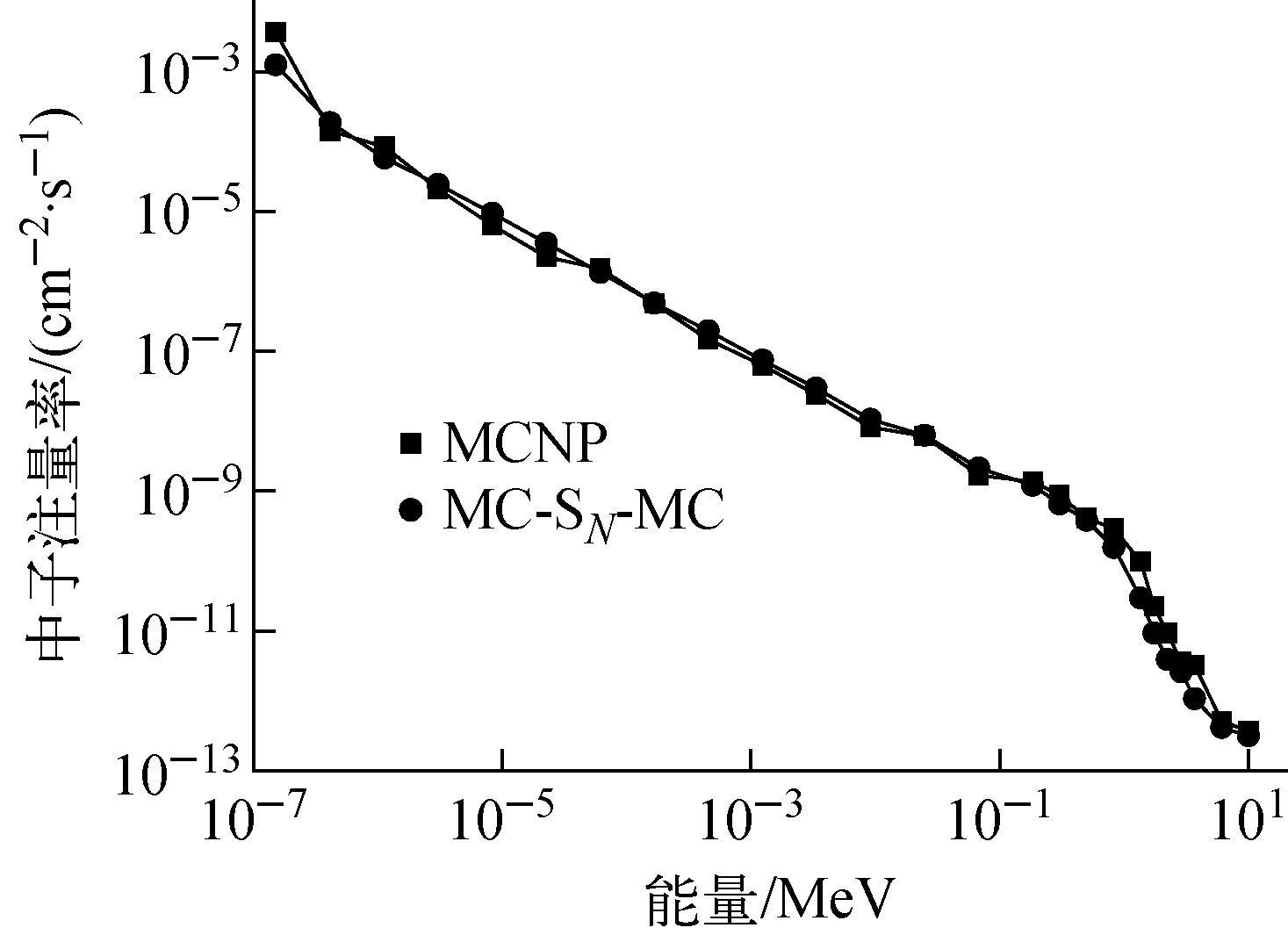
图5 P1处中子能谱

5 小结

为解决大尺寸复杂几何系统输运问题难以采用单一的模型及程序进行求解的难题，开发了三维蒙特卡罗-离散纵标双向耦合方法。将基于此耦合方法的MCNP-TORT-MCNP程序用于某压水堆堆坑粒子注量率计算，并与单一的MCNP程序计算进行比较，结果表明，蒙特卡罗-离散纵标双向耦合程序系统在速度和精度上均有很大优势，验证了三维蒙特卡罗-离散纵标双向耦合方法的正确性和可靠性。采用蒙特卡罗-离散纵标双向耦合程序系统使大型复杂核装置全三维屏蔽计算成为可能。

参考文献：

[1]CHEN Y, FISCHER U. Program system for three-dimensional coupled Monte Carlo: Deterministic shielding analysis with application to the accelerator-based IFMIF neutron source[J]. Nuclear Instruments and Methods in Physics Research A, 2005, 551: 387-395.

[2]韩静茹，陈义学，石生春，等. 基于离散纵标法与蒙特卡罗方法的三维耦合程序开发[J]. 核科学与工程，2012，32(2)：160-164.

HAN Jingru, CHEN Yixue, SHI Shengchun, et al. Development of three dimensional coupled code system based on discrete ordinates and Monte Carlo method[J]. Nuclear Science and Engineering, 2012, 32(2): 160-164(in Chinese).

[3]BRIESMEISTER J F. MCNP: A general Monte CarloN-particle transport code, version 4C, LA-13709-M[R]. USA: Los Alamos National Laboratory, 2000.

[4]RHOADES W A, SIMPSON D B. The TORT three-dimensional discrete ordinates neutron/photon transport code, ORNL/TM13221[R]. USA: Oak Ridge National Laboratory, 1997.

[5]刘桂莲. 秦山核电二期工程反应堆堆坑底部辐射通量分布计算[J]. 核动力工程，1998，19(4)：375-379.

LIU Guilian. Radiation flux calculation of reactor pit bottom in Qinshan Phase Ⅱ Nuclear Power project[J]. Nuclear Power Engineering, 1998, 19(4): 375-379(in Chinese).

[6]ROSSI H H. Protection against neutron radiation, NCRP-38[R]. US: National Council on Radiation Protection and Measurement, 1971.