线性空间中向量均衡问题解的最优性条件*
叶 琳, 仇秋生
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引 言
向量均衡问题包含向量优化、向量变分不等式等问题,一直受到广泛研究.Giannessi[1]首先在有限维空间中研究了向量变分不等式问题;文献[2]给出了无限维空间中的向量变分不等式并且把它应用于向量优化问题.随后越来越多的人开始把向量均衡问题扩展到抽象的空间,研究了不同情况下向量均衡问题的解的存在性[1]、灵敏性分析[3]、连续性[4]、连通性[5].最近,一些学者开始研究向量均衡问题的解的最优性条件.Giannessi等[6]把带约束的向量变分不等式问题转化成无约束的向量不等式问题,并给出了有限维空间中向量变分不等式的弱有效解的充分性和必要性条件;文献[7]在Banach空间中研究了向量变分不等式问题的近似解的最优性条件;文献[8]给出了锥凸条件下带约束的向量均衡问题的弱有效解、Henig有效解和超有效解的充分性和必要性条件;文献[9]在广义凸条件下得到了向量均衡问题的弱有效解的充分必要性条件;文献[10]在更弱的凸性下研究了Henig有效解的最优性条件.
线性空间是比拓扑空间更广的空间,但是很少有人研究线性空间中向量均衡问题的解的最优性条件,特别是对向量均衡问题的有效解的最优性条件的研究更少.本文首先给出线性空间中弱有效解的最优性条件;其次进一步研究了有效解的最优性条件;最后,以弱有效解为例给出了带约束的向量变分不等式的解的最优性条件.
1 定义和引理
本文假设X,Y,Z是实线性空间,C⊂Y和K⊂Z是点凸锥,Y*和Z*分别是Y和Z的代数对偶空间.因此,C的代数对偶锥和C的严格代数对偶锥分别为C*={y*∈Y*| 〈y*,y〉≥0,∀y∈C}和C+={y*∈Y*| 〈y*,y〉>0,∀y∈C{0}}.设M是Y中的非空子集,则M的锥包定义为coneM:=∪{tm:t≥0,m∈M}.
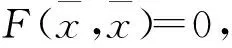

定义1[11]设N是Y中的非空子集,则N的代数内部、相对代数内部和代数闭集分别定义为:
corN={n∈N:∀v∈Y,∃t>0,∀α∈[0,t],n+αv∈N};
icrN={n∈N:∀v∈affN-n,∃t>0,∀α∈[0,t],n+αv∈N};
vclN={n∈N:∃v∈Y,∀λ′>0,∃λ∈(0,λ′],n+λv∈N}.


引理1[12]设C是Y中非平凡的点凸锥且corC≠Ø.若y∈corC,y*∈C*{0},则〈y*,y〉>0.
定义4[11,13]设D⊂X是非空子集,
1)若∀x1,x2∈D,∀λ∈(0,1),有λf(x1)+(1-λ)f(x2)∈f(D)+C,则称映射f:D→Y是C-似凸的.
2)若存在c∈corC,使得∀x1,x2∈D,∀λ∈(0,1),∀ε>0,有εc+λf(x1)+(1-λ)f(x2)∈F(D)+C,则称映射f:D→Y是C-次似凸的.
3)若存在c∈corC,使得∀x1,x2∈D,∀λ∈(0,1),∀ε>0,有εc+λf(x1)+(1-λ)f(x2)∈coneF(D)+C,则称映射f:D→Y是广义C-次似凸的.
定义5[11]设D⊂X是非空子集,若vcl(cone(f(D)+C))是Y中的凸集,则称映射f:D→Y在D上是近似C-次似凸的.
定义6[14]设D⊂X是非空子集,若1)cor(cone(f(D)+C))是Y中的凸集;2)cone(f(D)+C)⊆vcl(cor(cone(F(A)+C))),则称映射f:D→Y在D上是内部C-似凸的.
这几类广义凸性之间有以下关系:C-似凸⟹C-次似凸⟹广义C-次似凸,但反之不成立[13].
引理2[11]设D⊂X是非空子集,f:D→Y是映射,并设corC≠Ø.若f在D上是广义C-次似凸的,则f是近似C-次似凸的.
引理3[14]设D⊂X是非空子集,f:D→Y是映射.若corC≠Ø,则f在D上是内部C-似凸的当且仅当f是近似C-次似凸的.
引理4[15]设Y是线性空间,M,N⊂Y是2个凸集且M≠Ø,corN≠Ø.若M∩corN=Ø,则可用超平面将M与N分离.
引理5[15]设Y是线性空间,M⊂Y是凸集.若icrM≠Ø且0∉icrM,则可用超平面将0与M分离.
引理6[16]设Y是局部凸空间,C⊂Y是凸锥,c∈C,则c∈qiC当且仅当y*(c)>0,∀y*∈C*{0}.其中,qiC:={y∈C| cl(cone(C-y))=Y}.
2 最优性条件
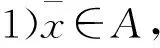
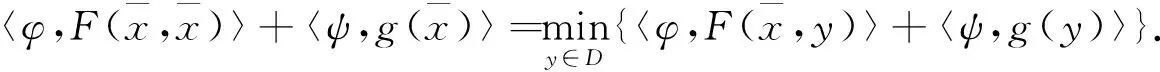
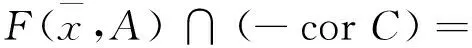
Ø.
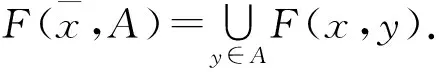
(h(D)+C×K)∩(-corC)×(-corK)=Ø.
(1)
若不然,则存在d∈D,c∈C和k∈K,使得

(2)
g(d)+k∈-corK.

由式(1)及C,K是点凸锥和corC,corK是代数开集得
vcl(cone(h(D)+C×K))∩(-corC)×(-corK)=Ø.
因h(y)在D上是近似C×K-次似凸的,所以vcl(cone(h(D)+C×K))是凸的.由引理4知,存在(φ,ψ)∈Y*×Z*{(0,0)}和β∈R,使得
〈(φ,ψ),vcl(cone(h(D)+C×K))〉≥β≥〈φ,-C〉+〈ψ,-K〉.
(3)

〈(φ,ψ),vcl(cone(h(D)+C×K))〉≥0.
(4)
而h(D)+C×K⊂vcl(cone(h(D)+C×K))且(0,0)∈C×K,故由式(4)有〈(φ,ψ),h(D)〉≥0,即
另外,(0,0) ∈vcl(cone(h(D)+C×K)),由式(3) 得
由C 是锥,∀c∈C,∀λ>0,得λc∈C,根据式(6) 有
〈φ,c〉≥1λ〈ψ,-k〉, ∀c∈C, ∀k∈K.
对固定的k,令λ→∞,有〈φ,c〉≥0,∀c∈C.因此,φ∈C*.同理可证ψ∈K*.
下证φ≠0.若φ=0,则ψ∈K*{0}.由式(5)得〈ψ,g(y)〉≥0,∀y∈D.由条件1),再根据引理1,有〈ψ,g(x0)〉<0.得出矛盾.故φ∈C*{0}.
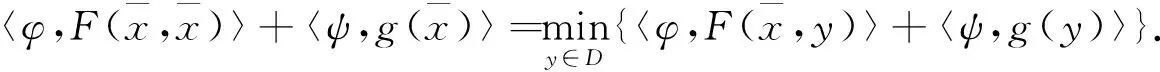



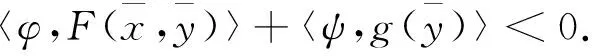
(7)


与式(7)矛盾.定理1证毕.
注1定理1是文献[9]中定理3.1在线性空间中的推广.
弱有效解仅在corC≠Ø时有意义,当corC=Ø时不能研究弱有效解.下面讨论有效解的最优性条件.
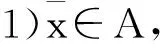
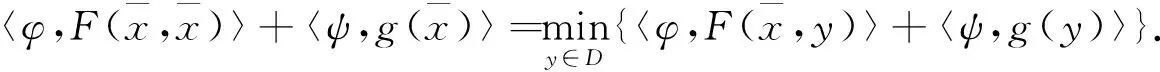

〈(φ,ψ),cor(cone(h(D)+C×K))〉≥0.
(8)
由此可得
〈(φ,ψ),vcl(cor(cone(h(D)+C×K)))〉≥0.
(9)

(10)


由式(8)得
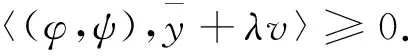
(11)
当λ′充分小时,由式(10)得

与式(11)矛盾.
由h(y)在D上是内部C×K-似凸的,有
h(D)+C×K⊂cone(h(D)+C×K)⊂vcl(cor(cone(h(D)+C×K))).
根据式(9)有
〈(φ,ψ),h(D)+C×K〉≥0.
(12)
再由(0,0)∈C×K及式(12)有〈(φ,ψ),h(D)〉≥0,即
且
若不然,存在(c,k)∈C×K,使得〈(φ,ψ),(c,k)〉<0.由C×K为锥知,对λ>0,有λ(c,k)∈C×K.因此,对给定的y∈D,当λ充分大时有〈(φ,ψ),h(y)+λ(c,k)〉< 0.与式( 12) 矛盾,因此,式( 14) 成立.再由C是锥知,对任意λ>0,有
〈φ,c〉≥-1λ〈ψ,k〉, ∀c∈C, ∀k∈K.
对固定的k,令λ→∞,则
〈φ,c〉≥0, ∀c∈C.
因此,φ∈C*,同理可证ψ∈K*.
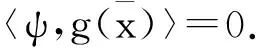
注2当Y和Z是有限维空间时,由于cor(cone(h(D)+C×K))是非空凸集,显然有icr(cor(cone(h(D)+C×K)))≠Ø.当Y和Z是局部凸空间时,由于锥包内部非空,由开凸集分离定理即可得到结论.因此,当Y和Z是有限维空间或局部凸空间时,条件icr(cor(cone(h(D)+C×K)))≠Ø可以去掉.
注3定理2中corC可为空集,icr(cor(cone(h(D)+C×K)))≠Ø比corC≠Ø条件更弱.因为当corC≠Ø时,由corK≠Ø可知cor(C×K)≠Ø,则cor(cor(cone(h(D)+C×K)))=cor(cone(h(D))+cor(C×K))=cone(h(D))+cor(C×K)≠Ø,所以icr(cor(cone(h(D)+C×K)))≠Ø.
设Y和Z是局部凸空间,则可得到下面的定义:
定义7[17]设D⊂X是非空子集,映射f:D→Y.若1)int(cone(f(D)+C))是Y中的凸集;2)f(D)+C⊆cl(int(cone(F(A)+C))),则称映射f:D→Y在D上是内部C-似凸的.
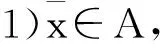
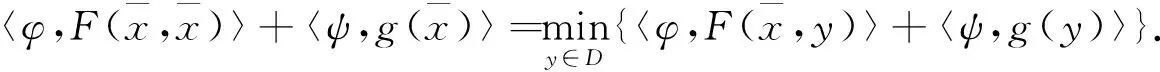

由h(y)在D上是内部C×K-似凸的知,int(cone(h(D)+C×K))是凸的,由凸集分离定理知,存在(φ,ψ)∈Y*×Z*{(0,0)},使得〈(φ,ψ),int(cone(h(D)+C×K))〉>0,由此可得
〈(φ,ψ),cl(int(cone(h(D)+C×K)))〉≥0.
类似于定理2的证明,可得
〈ψ,g()〉=0,
(16)
及φ∈C*和ψ∈K*.

注41)在定理3中,intC,intK可为空集.例如,K为lp或Lp(1 2)若K为内部非空的凸锥,则intK=qiK. (17) 与式(17)矛盾.定理4证毕. 下面将给出定理1在向量变分不等式问题中的应用. (Tx,y-x)∉-C{0}, ∀y∈A. 其中,T:D→L(X,Y)是向量值映射.显然,(VVIC)就是(VEPC)当F(x,y)=(Tx,y-x),x,y∈D时的特殊情况. 注5用类似的方法可以得到向量变分不等式问题的有效解的最优性条件. 注6若F(x,y)=f(y)-f(x),x,y∈D,则可以获得向量优化问题的最优性条件. 参考文献: [1]Giannessi F.Theorem of alternative,quadratic programs and complementarity problem[C]//Cottle R W,Giannessi F,Lions J L.Variational inequality and complementarity problem.Wiley:Chichester,1980:151-186. [2]Chen Guangya,Cheng Gingmin.Vector variational inequality and vector optimization[C]//Bechmann M,Kunzi H P.Lecture notes in economics and mathematical systems.New York:Springer,1987:408-416. [3]Kimura K,Yao J C.Sensitivity analysis of vector equilibrium problems[J].Taiwanese J Math,2008,12(3):649-669. [4]Kimura K,Yao J C.Semicontinuity of solution mappings of parametric generalized strong vector equilibrium problems[J].J Ind Manag Optim,2008,4(1):167-181. [5]Gong X H,Yao J C.Connectedness of the set of efficient solutions for generalized systems[J].J Optim Theory Appl,2008,138(2):189-196. [6]Giannessi F,Mastroeni G,Pellegrini L.On the theory of vector optimization and variational inequalities.Image space analysis and separation[C]//Giannessi F.Vector variational inequalities and vector equilibria:mathematical theories.Dordrecht:Kluwer Acad Publ,2000:153-215. [7]Yang X Q,Zheng X Y.Approximate solutions and optimality conditions of vector variational inequalites in Banach space[J].J Global Optim,2008,40(1):455-462. [8]Gong Xunhua.Optimality conditioins for vector equilibrium problems[J].J Math Anal Appl,2008,342(2):1455-1466. [9]Qiu Qiusheng.Optimality conditions for vector equilibrium problems with constration[J].J Ind Manag Optim,2009,5(4):783-790. [10]Long X J,Huang Y Q,Peng Z Y.Optimality condition for the Henig efficient solution of vector equilibrium problems with constraints[J].J Optim Lett,2011,5(4):717-728. [11]Adán M,Novo V.Weak efficiency in vector optimization using a closure of algebraic type under cone-convexlikeness[J].European Journal of Operational Research,2003,149(3):641-653. [12]Li Zemin.The optimality conditons for vector optimization of set-valued maps[J].J Math Anal Appl,1999,237(1):413-424. [13]Zhou Z A,Peng J W.Scalarization of set-valued optimization problems with generalized cone subconvexlikeness in real ordered linear spaces[J].J Optim Theory Appl,2012,154(3):830-841. [14]Zhou Zhiang.The relationship between two kinds of generalized convex set-valued maps in real ordered linear spaces[J/OL].J Abst Appl Anal,2013,2013:105617.(2013-03-12)[2013-05-14].http://dx.doi.org/10.1155/2013/105617. [15]史树中.凸分析[M].上海:上海科技大学出版社,1990. [16]Gong Xunhua.Optimality conditioins for Henig and globally proper efficient solutions with ordering cone has empty interior[J].J Math Anal,2005,307(1):12-31. [17]Sach P H.New generalized convexity notion for set-valued maps and applicatin to vector optimization[J].J Optim Theory Appl,2005,125(1):157-179.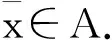
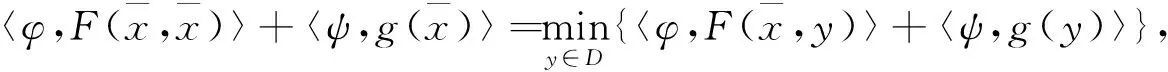



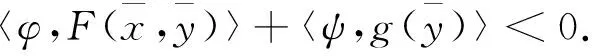


3 应 用