基于摩擦效应的砂岩裂缝密度定量预测
宋 璠,苏妮娜,冯建伟,罗彩明,陈静静,宋明福
(1.中国石油大学地球科学与技术学院,山东青岛266580;2.中石油塔里木油田勘探开发研究院,新疆库尔勒841000;3.胜利油田鲁明油气勘探开发有限公司,山东东营257001)
随着油气勘探开发逐渐向非常规储层转移,寻找裂缝性储集层已成为热点,其中如何预测构造裂缝及其参数的空间分布是该领域的前沿问题。构造裂缝主要受控于构造应力场和岩石物理性质,目前主要采用应力场分析法进行预测,此外还有构造曲率法、测井分析法、应变量分析法等[1-4]。王仁等[5]尝试从应力场角度出发,以岩石破裂准则为依据进行裂缝预测;丁中一等[6]基于裂缝产生机制,提出了二元法裂缝预测方法;随着地质力学和应力场模拟技术的发展,出现了基于三维构造模型的裂缝数值模拟技术[7-9];国内外学者基于岩石破裂准则,提出了多元统计法定量计算裂缝密度和开度,将裂缝预测技术提高到了新的水平[10-11];戴俊生等[12]提出了基于古、今应力场改造叠加效应的裂缝定量预测方法,并通过岩石力学实验建立了应力-应变和裂缝参数之间的定量模型,并提出裂缝表面能的概念,推动储层裂缝研究技术迈上新的台阶。前人通过应力场进行裂缝预测取得了一定成果,但也存在许多问题,例如在脆性砂岩中,当发生压性剪切破裂时,裂缝开裂后裂缝面上仍有残余应力存在,这部分应力形成了摩擦阻力,并且在裂缝继续扩展过程中消耗一部分弹性能。前人在重视能量守恒和应变产生裂缝的同时,忽略了岩石变形过程中这种能量的转换与传递的关系。笔者选取准噶尔盆地某砂岩储层为对象,在岩石力学实验的基础上,分析岩石受力变形过程中能量的转换关系,在考虑裂缝面摩擦能的情况下,结合单轴压缩状态下应力-应变和裂缝密度的关系,推导复杂应力条件下砂岩裂缝体密度的解析表达式,建立应力-应变与裂缝密度的力学模型,指导应力场数值模拟,从而提高裂缝参数的预测精度。
1 岩石力学实验
深埋于地下的岩石在漫长的地质时间内不断发生变形,通常在一定的温压条件下,快速单轴压缩易形成平行于受力方向的张性断裂,而慢速单轴压缩主要形成剪性断裂[13]。为了研究砂岩受力变形直至破裂过程中的能量转换关系,分别设计了单轴、三轴压缩实验,选取准噶尔盆地某油田近20块胶结致密的低渗砂岩样品,参照“国际岩石力学协会”岩石力学测试标准进行制样,以恒应变速率进行加载、卸载和全过程岩石力学实验,同时用AE210声发射测试系统测量其声发射能。通过实验获取各样品的密度以及在不同围压条件下的强度等参数(表1),绘制相应的应力-应变曲线(图1)。

表1 砂岩样品力学性质实验结果Table 1 Results of mechanical property experiment of sandstone

图1 砂岩样品单轴、三轴实验应力-应变曲线Fig.1 Stress-strain curves of single axis and three axis experiment of sandstone

图2 砂岩压缩实验应力-应变曲线Fig.2 Stress-strain curve of compression test on sandstone
在岩石力学实验的基础上,对剩余样品施加分别为单轴压缩强度的10%、20%、30%直至90%的最大载荷,进而磨片进行裂缝观察与统计,发现随着压缩强度增大,砂岩样品微裂缝具有如下演化特征(图2)。在压密段(OA段),砂岩样品中的微裂缝被压缩,裂缝开度、渗透性均大幅降低,砂岩变得致密坚硬;AB段为岩样弹性形变阶段,应力-应变曲线近似呈直线,样品中无明显的张裂缝,少数杂乱的微裂纹开度延伸不足0.2mm,主要为网状的粒内缝;BC段又称扩容段,此阶段径向应变明显增加,B点代表岩石的屈服极限,对应的应力σs是峰值应力σc的0.85倍,镜下观察表明当应力大于0.85σc时出现大量方向性显著的微裂缝;当应力达到峰值应力σc时,岩样发生宏观破裂,应力逐渐降低。
上述实验表明:砂岩样品承受低载荷初期,前期微裂缝发生闭合,随着应力增加形成新的微裂缝,造成径向扩容显著。大量前兆微裂缝出现时间的对应于峰值应力的0.85倍,相应应力开始出现回落现象,表明在总能量缓慢增加的情况下,裂缝随着延伸长度的增加,缝面之间出现了摩擦耗能。综合实验成果编绘微裂缝形态随应力变化示意图(图3),图中σc为峰值应力,ε为岩样的轴向应变,εc为峰值应力的应变值。可以看出,OA-AB区属于压密及弹性形变阶段,无明显微裂缝形成;当应力达到0.85σc时,进入体积扩容阶段(BC区),微裂缝数量显著增加,且具有明显的方向性,其中与轴向应力方向呈较小角度(小于等于30°)的微裂缝生成速度最快;CD区为岩样破坏阶段,宏观裂缝形成,裂缝的开度、密度均有所增加。

图3 砂岩样品微裂缝随应力增加的发展过程Fig.3 Developing process of micro-fractures in sandstone under increasing stress
2 岩石变形过程中能量的转换关系
岩石受力后产生应变,使得能量不断积聚,最终导致岩石变形破坏。另一方面,岩石在变形破坏过程中会伴随能量的耗散和释放,岩石中弹性能的增加会造成岩石破坏驱动能量增加,而非线性能量耗散会使得岩石的破坏阈值降低。释放能量包括声波能、动能和摩擦热能,由于相对于断裂来说裂缝产生的声波能很小,一般忽略不计,因此摩擦热能占主导地位。陈旭光等[14]以实验为基础证明了摩擦耗能的存在,并认为脆性岩石中摩擦耗能随着岩石内摩擦角的增加而增大,约占总能量的30%~40%。拉张裂缝形成过程中除了能量转化为裂缝外,剩余的能量仍残留在岩石中;剪切裂缝则不同,在裂缝产生、能量释放的一瞬间,裂缝面发生相对运动。
2.1 能量转换原理
根据弹性力学原理,岩石在受力时,外界会以力作用施加的方式将能量传递到岩石内部储存起来,随着岩石发生破坏,能量会以非线性变化的方式释放和耗散掉。能量耗散一般有两种方式:一是裂缝表面能产生单位面积裂缝所需要的能量;二是岩石内部微裂纹尖端区域的塑性变形消耗能,主要位于裂纹尖端区[15]。岩石将外界输入的能量以弹性形变能的方式积累,存储到一定程度后突然向外界剧烈释放,释放的能量包括声波能、动能、摩擦热能等多种形式。整个过程可以表示为:U=Ue+Us+Uf+Um+Ua,其中Ue为岩石的弹性能,为由外力引起的储存能量,Us为塑性变形能,Uf为形成裂缝需要的表面能,Um为裂缝面产生后的摩擦耗能,Ua为其他一切尚未被发现或定义的能量部分。
假设岩石处于正常压缩状态,在三轴压力作用下,获得的总能量为

式中,U为输入岩石的总能量,即对岩石作的功,可由应力 -应变曲线求得,J;σ1、σ2和σ3分别为最大、中等和最小主应力,MPa;ε1、ε2和ε3分别为相应的3个主应变。可以得出存储的弹性应变能为

弹性应变服从胡克定律,由此可得

其中,E为弹性模量,MPa。将(3)、(4)和(5)代入(2)得到由主应力表示的弹性应变能为

2.2 能量转换关系
对于单轴压缩,岩石样品会发生沿着与轴向呈大约30°的方向破裂。单轴表达式为,由于岩石发展到弹性破裂之前主要是以弹性变形为主,只有裂纹区会发生一定塑性变形,而脆性岩石样品的塑性能比例很小,可以忽略,弹性变形区不消耗弹性能,只有裂缝产生损耗的裂缝表面能,因此岩石加载过程中存储的弹性应变能为

随着裂纹的扩展逐渐形成宏观裂缝,由于裂纹尖端应力的集中产生塑性变形区,剪切裂纹尖端的3个主应力分别为

式中,σ12为裂纹尖端剪应力,MPa;σ11和σ22为裂纹尖端主应力,MPa;K∏为二类强度因子;r为裂纹尖端矢径,m;θ为裂纹尖端夹角;σn为裂纹间相互压力,MPa;σf为裂纹完全贯通后新形成两断面间的剩余摩擦力,MPa。
为了建立复杂状态下岩石裂缝体密度与应力、应变的关系,选取边长分别为L1、L2、L3的平行六面表征单元体进行研究,且有正应力σ1>σ2>σ3(图4)。单元体在应力作用下产生裂缝,由库伦 -莫尔强度原理可知,裂缝的主方向与最大主应力成θ角,,φ为内摩擦角。根据弹性力学理论认为裂纹尖端表面的剪切滑动位移为:L=(1-μ)/GK∏(8r/π)1/2,其中G为剪切模量,则裂缝从开始到贯穿所需要的表面能为
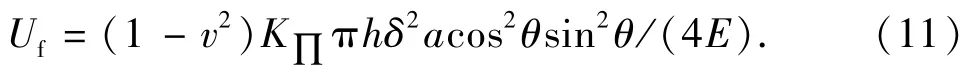

图4 表征单元体内应力方向及裂缝形态Fig.4 Stress direction and fracture pattern of unit body
在裂缝即将产生的临界区,裂缝面之间依靠摩擦力维系稳定,当裂缝瞬间产生并滑动时,裂缝面存在正应力和剪切力,需要消耗一部分能量,另一部分转化为热能,则摩擦力作功为
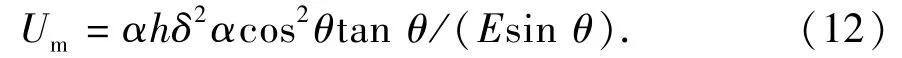
式中,a为裂缝贯穿后的长度。2hacosθ为岩石内六面体单元的体积,因此裂缝产生之前累积的应变能为,岩石破坏裂缝产生并停止前的释放能为
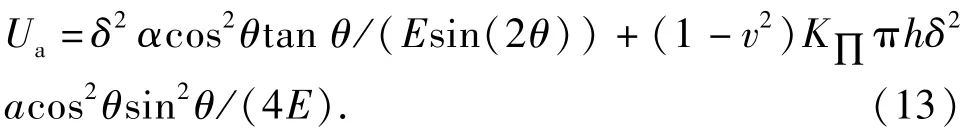
据弹性力学理论,固体变形时在其内部只能积聚弹性应变能,固体内部的应变能可用应变能密度来衡量,故将(6)式改写为

释放后一部分用来抵消新增裂缝表面积需要的表面能量,一部分用来克服缝面,其他的可忽略不计,故根据能量守恒原理可建立公式:

式中,V为表征单元体体积,m3;f为新增裂缝表面积的应变能密度,J/m3;m为新增裂缝表面积的摩擦能密度;S为新增裂缝表面积,m2;J为裂缝总表面能,J/m2。将上式变换可得单元体内裂缝体密度Dvf为

式中,e为弹性应变能密度,J/m3;转换后的均为应变系数,可通过物理概念方程或实验数据拟合求取。物理概念方程物理意义明确,只需少量数即可获得需要的结果,然而其准确度缺乏有效验证手段;第二种方法通常要大量的实验数据才能获得较好的参数值,准确性较好。
3 裂缝密度与应力-应变的关系
3.1 单轴压缩状态下的关系
岩石力学实验表明,单轴压缩下应力值0.85σc是大量微裂缝出现的临界点,对应的应变能密度值与式(16)中的e相似。假设临界应变能密度为e,摩擦耗能密度为m,代入公式求解J值以及a、b、c参数。由岩石力学测试结果求得0.85σc=36.28 MPa、e=1.133 kJ/m3、m=0.341 kJ/m3,代入式(16)即可建立裂缝体密度与应变能密度的关系为Dvf=9.2×10-4-104.2。
3.2 复杂应力状态下的关系
实际情况下,地下岩石常处于三轴复杂应力状态,需要对上述公式进行校正。三轴压应力状态下,产生裂缝必须克服的弹性应变能密度除与岩石本身的力学性质有关以外,还与其周围的应力环境有关。岩石力学实验表明三轴压缩曲线与单轴曲线特征具有一定相似性,因此在综合考虑围压及摩擦效应的条件下,推导出三轴压缩状态下应力 -应变与产生裂缝体密度的关系为

式中,J0为代表围压值为0时的裂缝表面能,其数值与单轴压缩实验结果相等,J;ΔJ为代表围压所产生的附加表面能,J;J1为代表附加摩擦能,J。
为了验证公式(17)的准确性,以陶振宇等[16]开展的砂岩真三轴实验结果为基础,利用该公式计算裂缝体密度,并与实测密度值进行对比,结果表明样品相对误差较小(表2),证实计算方法的有效性。

表2 三轴压缩状态下裂缝体密度计算结果与实验结果对比Table 2 Contrasts of calculate and test results of fracture density under three axis stress
综上所述,当砂岩地层承受挤压应力时,裂缝的形成除了要克服由分子间作用力形成的内在黏聚力外,还要克服围压与摩擦效应形成的阻力,可使用库仑-莫尔破裂准则进行岩石破裂判别,进而利用式(17)进行岩石内应力 -应变和裂缝密度关系的计算,其中黏聚力和内摩擦角可以通过莫尔包络线求出。
此外,对于挤压型盆地,局部也存在一些张应力,此时岩石的脆性特征更为明显,力学实验表明在张应力未达到峰值强度前,应力 -应变呈线性相关,而超到峰值应力σc后迅速降至0,样品迅速破裂,未形成前兆微裂缝[17]。因此当张应力存在时,岩石受力后会出现张剪破裂、张破裂等多种破裂方式,破裂条件需要利用格里菲斯准则进行判别,应力-应变与裂缝密度的推导关系也需适当修正。式(16)中的弹性应变能密度e可利用单轴拉伸时峰值应力所对应的应变能密度来代替,进而推导出拉张应力条件下裂缝体密度计算公式为
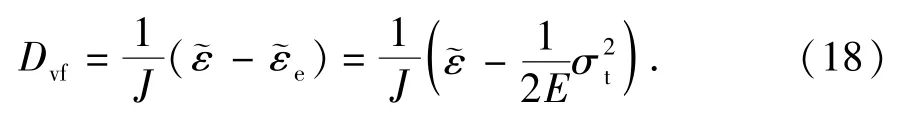
4 应用实例
以准噶尔盆地西北缘二叠系低渗砂岩储层为例,其岩性主要为中—细砂岩以及泥质粉砂岩。地层埋深4000~5000 m,早期经历了强烈的推覆挤压变形,主要发育逆冲断裂,形成了大量高角度裂缝以及直立缝。为了研究裂缝的分布密度,以岩石力学实验为基础,采用上述理论计算模型,借助ANSYS应力场模拟软件进行模拟,实现了基于应力、应变并考虑摩擦效应的裂缝密度定量预测。
对研究区砂岩样品进行声发射测试,结果表明新生代岩石记录了500 MPa和300 MPa两期应力值,分别对应二叠纪末和三叠纪末,其中二叠纪末为主要造缝期。根据最大主应力方向与共轭裂缝锐夹角的平分线方向相同的原则,认为二叠世裂缝形成时期的最大主应力为北西-南东向。同时,由裂缝形成和发育的时间可计算出裂缝产生时期的埋藏深度,进而估算重力值,利用破裂准则法求取最大主应力。二叠系造缝期时地层埋藏较浅[18],利用公式F=ρgh计算出火山岩产生的垂向压力为0~97.7 MPa,根据库仑-摩尔破裂准则最终求得σ1≥486 MPa。
由构造平面图和剖面图建立三维有限元模型,并进行边界约束,边界力主要包括水平构造力、重力、上覆岩层压力。在进行古应力场模拟时对南北方向反复加载,观察模型的变形结果,拟合出接近于现今构造的加载方案,即北西-南东315°方向为最大主应力方向,为500 MPa;北东-南西向为中间主应力方向,为150 MPa;垂向为最小主应力方向,由自身重力产生。通过古、今应力场数值模拟,并将应力、应变数据导入上述裂缝密度计算模型,预测该地区二叠系裂缝密度分布。结果显示:二叠纪末古应力场有明显的分带性(图5),西部百乌井区古应力场整体受背斜影响较大,以背斜区附近最大主应力偏小为主要特征;东部夏字井区出现应力高值区,高于590 MPa;中部风字号井区表现为应力低值区,约为550 MPa。由此可见东部最大主应力值较西部高,表现出强烈的挤压特性。裂缝整体分布广泛,区内裂缝线密度变化较小,平均约为15条/m,裂缝相对较少的地区一般大于5条/m(图6)。结合应力分布可以看出:挤压应力相对低的部位,由于张应力的存在,裂缝也可大量发育;强挤压区裂缝发育密度并不一定最大,主要由于挤压增加了裂缝面的摩擦耗能,占释放能量的比重较大。

图5 模拟区古应力场最大主应力分布Fig.5 Distribution of maximum principal paleostress of modeling area

图6 模拟区裂缝线密度分布Fig.6 Distribution of fracture linear density of modeling area
5 结 论
(1)岩石在受力变形过程中,能量会以非线性变化的方式释放和耗散,能量的耗散一般有裂缝表面能产生单位面积裂缝所需要能量和岩石内部微裂纹尖端区域的塑性变形消耗能两种方式。其中摩擦耗能最为重要,随着岩石内摩擦角的增大而增大,平均占总释放能量的30%~40%。
(2)脆性砂岩内破裂是颗粒内部或颗粒间微裂隙进一步发展、集结的结果。砂岩样品承受低载荷初期,前期微裂缝发生闭合,随着应力增加形成新的微裂缝,造成径向扩容显著。大量前兆微裂缝出现时间对应于峰值应力的85%,相应应力开始出现回落现象,表明在总能量缓慢增加的情况下,裂缝随着延伸长度的增加,缝面之间出现了摩擦耗能。
(3)当砂岩地层中不存在拉张应力时,可使用库仑-莫尔破裂准则进行岩石破裂判别,在判别的基础上进行岩石内应力-应变和裂缝密度关系的计算;当有张应力存在时,破裂条件需要利用格里菲斯准则进行判别,应力-应变与裂缝密度的关系也需修正。
[1] 周新桂,张林炎,范昆.油气盆地低渗透储层裂缝预测研究现状及进展[J].地质论评,2006,52(6):777-782.ZHOU Xingui,ZHANG Linyan,FAN Kun.The research situation and progresses of natural fracture for low permeability reservoirs in oil and gas basin[J].Geological Re-view,2006,52(6):777-782.
[2] 刘金华,杨少春,陈宁宁,等.火成岩油气储层中构造裂缝的微构造曲率预测法[J].中国矿业大学学报,2009,38(6):815-819.LIU Jinhua,YANG Shaochun,CHEN Ningning,et al.Forecasting method of tectoclase in the igneous reservoirs using a curvature of the microtectonics[J].Journal of China University of Mining&Technology,2009,38(6):815-819.
[3] 孙建孟,闫国亮,姜黎明,等.基于数字岩心研究流体性质对裂缝性低渗透储层弹性参数的影响规律[J].中国石油大学学报:自然科学版,2014,38(3):39-44.SUN Jianmeng,YAN Guoliang,JIANG Liming,et al.Research of influence laws of fluid properties on elastic parameters of fractured low permeability reservoir rocks based on digital core[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(3):39-44.
[4] 牛虎林,胡欣,徐志强,等.基岩油气藏裂缝性储层的成像测井评价及裂缝预测[J].石油学报,2010,31(2):264-269.NIU Hulin,HU Xin,XU Zhiqiang,et al.Evaluation of imaging logging and fracture prediction in fractured basement reservoirs[J].Acta Petrolei Sinica,2010,31(2):264-269.
[5] 王仁.有限单元等数值方法在我国地球科学中的应用和发展[J].地球物理学报,1994,37(1):128-139.WANG Ren.Application and development of finite element and other numerical simulation methods in earth sciences in China[J].Acta Geophysica Sinica,1994,37(1):128-139.
[6] 丁中一,钱祥麟,霍红,等.构造裂缝定量预测的一种新方法:二元法[J].石油与天然气地质,1998,19(1):1-7.DING Zhongyi,QIAN Xianglin,HUO Hong,et al.A new method for quantitative prediction of tectonic fractures—two-factor method[J].Oil&Gas Geology,1998,19(1):1-7.
[7] 吴时国,王秀玲,季玉新,等.3Dmove构造裂缝预测技术在古潜山的应用研究[J].中国科学D辑:地球科学,2004,34(9):795-806.WU Shiguo,WANG Xiuling,JI Yuxin,et al.Applications of 3Dmove tectonic fracture prediction in buried hill[J].Science in China(ser D):Earth Sciences,2004,34(9):795-806.
[8] 孙致学,姚军,樊冬艳.基于离散裂缝模型的复杂裂缝系统水平井动态分析[J].中国石油大学学报:自然科学版,2014,38(2):109-115.SUN Zhixue,YAO Jun,FAN Dongyan.Dynamic analysis of horizontal wells with complex fractures based on a discrete-fracture model[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(2):109-115.
[9] 张亚中,周晶,李建华,等.青西凹陷青南次凹裂缝性储层地震综合预测[J].石油地球物理勘探,2009,44(2):225-230.ZHANG Yazhong,ZHOU Jing,LI Jianhua,et al.Seismic integrative prediction of fractural reservoir in Qingnan sub-sag of Qingxi sag[J].Oil Geophysical Prospecting,2009,44(2):225-230.
[10] 闫相祯,王志刚,刘钦节,等.储集层裂缝预测分析的多参数判据法[J].石油勘探与开发,2009,36(6):749-755.YAN Xiangzhen,WANG Zhigang,LIU Qinjie,et al.Reservoir fracture prediction by multi-parameter criteria method[J].Petroleum Exploration and Development,2009,36(6):749-755.
[11] GRAY D,HEAD K V.Fracture detection in the Manderson field:a 3D AVAZ case history[J].Leading Edge,2000,19(11):1214-1221.
[12] 戴俊生,汪必峰.综合方法识别和预测储层裂缝[J].油气地质与采收率,2003,10(1):1-3.DAI Junsheng,WANG Bifeng.Integrated approach of identifying and predicting fracture in reservoir[J].Petroleum Geology and Recovery Efficiency,2003,10(1):1-3.
[13] 张惠良,张荣虎,杨海军,等.构造裂缝发育型砂岩储层定量评价方法及应用:以库车前陆盆地白垩系为例[J].岩石学报,2012,28(3):827-835.ZHANG Huiliang,ZHANG Ronghu,YANG Haijun,et al.Quantitative evaluation methods and applications of tectonic fracture developed sand reservoir:a Cretaceous example from Kuqa foreland basin[J].Acta Petrologica Sinica,2012,28(3):827-835.
[14] 陈旭光,张强勇.岩石剪切破坏过程的能量耗散和释放研究[J].采矿与安全工程学报,2010,27(2):179-184.CHEN Xuguang,ZHANG Qiangyong.Research on the energy dissipation and release in the process of rock shear failure[J].Journal of Mining&Safety Engineering,2010,27(2):179-184.
[15] 季宗镇,戴俊生,汪必峰,等.构造裂缝多参数定量计算模型[J].中国石油大学学报:自然科学版,2010,34(1):24-28.JI Zongzhen,DAI Junsheng,WANG Bifeng,et al.Muti-parameter quantitative calculation model for tectonic fracture[J].Journal of China University of Petroleum(Edition of Natural Science),2010,34(1):24-28.
[16] 陶振宇,朱焕春,高延法,等.岩石力学的地质与物理基础[M].北京:中国地质大学出版社,1996:20-23.
[17] 王平.含油盆地构造力学原理[M].北京:石油工业出版社,2001:44-48.
[18] 王军,戴俊生,冯建伟,等.乌夏断裂带二叠系火山岩碎屑岩混杂地层裂缝预测[J].中国石油大学学报:自然科学版,2010,34(4):19-24.WANG Jun,DAI Junsheng,FENG Jianwei,et al.Fracture prediction of Permian volcanic-clastic rock formation in Wuxia fault belt[J].Journal of China University of Petroleum(Edition of Natural Science),2010,34(4):19-24.
——以淮南矿区为例

