游梁式抽油机传动系统的扭转振动与传动效率

邢明明,董世民

(燕山大学机械工程系,河北秦皇岛066004)

游梁式抽油系统的节能降耗一直是国内外专家学者关注的重点。进行系统参数的动态仿真、实现参数最优化组合是提高有杆抽油系统的系统效率、降低能量损耗的有效方法[1-5]。以系统动态仿真为基础的抽油机井节能仿真优化技术已经广泛应用于油田实践[6-10]。游梁式抽油机井动态仿真模型包括[5-7]：游梁式抽油机地面装置动力学仿真模型和井下杆管液柱耦合振动仿真模型。目前在研究游梁式抽油系统地面装置的动力学时，未考虑地面传动系统的弹性，将游梁式抽油系统地面装置简化为单自由度的等效曲柄，建立了电动机转子或曲柄瞬时运动规律的仿真模型[5-7]。根据曲柄运动规律的仿真结果，可以进一步分析抽油机各运动部件的运动规律[1，8-10]。皮带减速箱平均运行效率的计算机仿真结果约为85%[9]，而实际皮带减速箱的平均传动效率仅为68.47%～82%，可见取皮带减速箱的传动效率为常数会直接影响仿真精度。为此，笔者以游梁式抽油机皮带减速箱传动系统为研究对象，考虑皮带减速箱传动系统的弹性，建立皮带减速箱传动系统扭转振动的仿真模型，以完善游梁式抽油机地面装置的动力学仿真模型，提高抽油机井动态参数的仿真精度。

1 传动系统的力学与数学模型

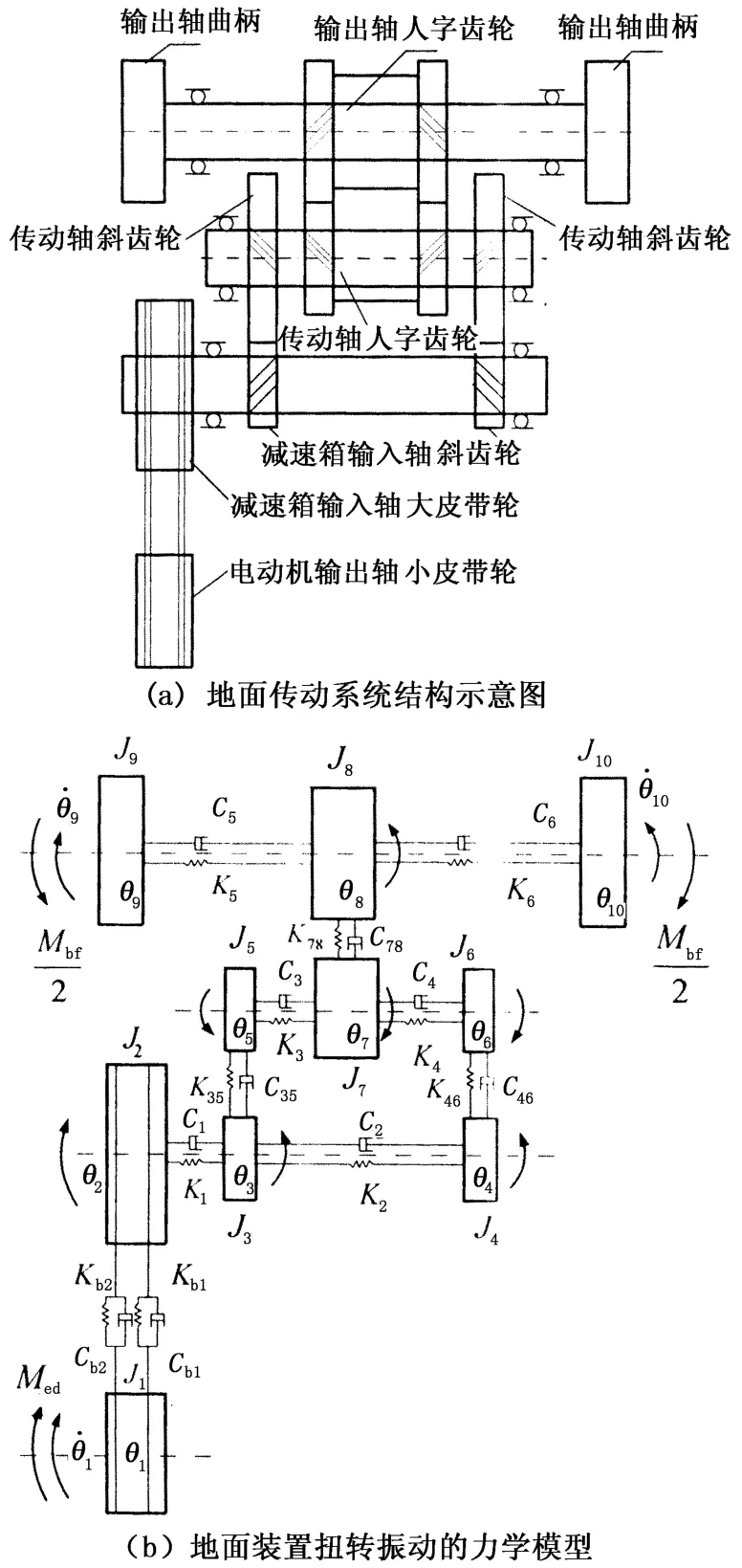
图1 抽油机地面传动系统力学模型Fig.1 Mechanical model of surface transmission system for beam pumping unit

游梁式抽油系统的地面装置由电动机、皮带减速箱传动系统与曲柄摇杆换向机构组成。图1为抽油机地面传动系统力学模型。为便于研究，做如下假设和简化：①不考虑各传动轴支撑部分的弹性变形；②将皮带简化为无质量的抗拉弹簧；③只考虑减速箱传动系统的扭转振动，不考虑各传动轴的横向振动；④齿轮轮齿为线弹性体，考虑轮齿弯曲对传动系统扭转刚度的影响；⑤不考虑齿面啮合误差对齿轮系统的内部激励；⑥带轮与齿轮体为刚性体，并将各个带轮、齿轮简化为刚性圆盘，其轴向位置位于带轮、齿轮的轴向对称面处；⑦将相邻两圆盘之间的轴段简化为无质量的抗扭弹簧，并将该轴段的转动惯量简化到相邻圆盘上；⑧曲柄轴净扭矩Mbf均匀地分配到两个曲柄上。

建立图1(b)所示的传动系统扭转振动的力学模型。

图中，Ji为各构件等效转动惯量；Kb1、Kb2分别为皮带的紧边和松边等效拉伸刚度；Cb1、Cb2分别为皮带的紧边和松边等效阻尼；Ki、Ci分别为传动轴等效扭转刚度及等效阻尼；Kij、Cij分别为齿轮副的啮合刚度及啮合阻尼；θi为各圆盘的转角；Mbf为曲柄轴净扭矩(曲柄轴处的等效阻力矩)；Med为电动机输出轴扭矩(小皮带轮处的等效驱动力矩)。

根据Lagrange方程，可以建立图1(b)所示的游梁式抽油机皮带减速箱传动系统的运动微分方程为

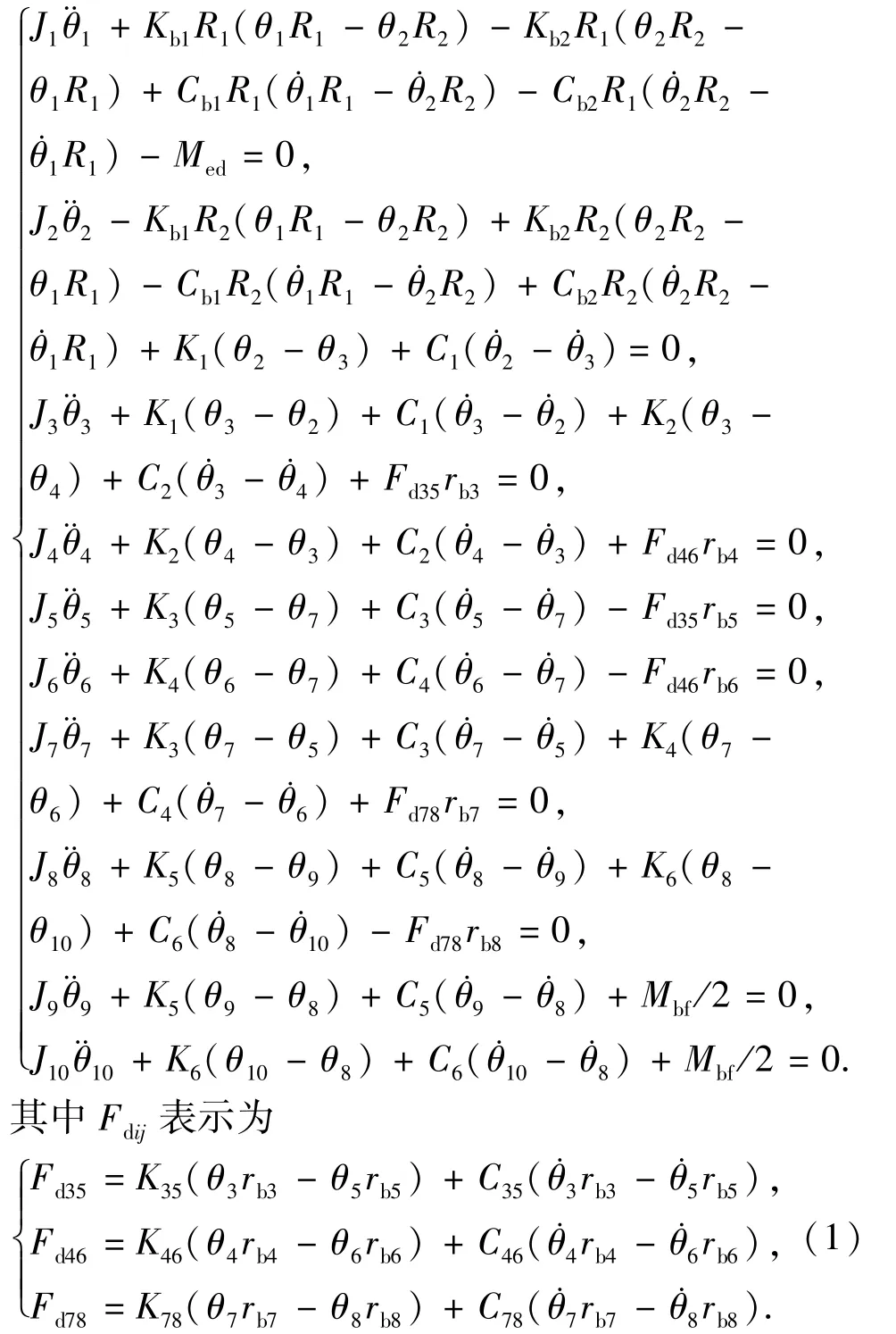
式中，rbi为各齿轮或齿轮轴的齿根圆半径，m；Fdij为轮齿的动态啮合力，N。

1.1 等效驱动力矩和等效阻力矩

根据电动机的额定参数，等效驱动力矩[8]为

式中，MH为系统动力输入电机的额定转矩，N·m；ω0为动力输入电机的同步角速度，rad/s；λk为动力输入电机的过载系数；PH为额定功率，kW；n0为同步转速，r·min-1；nH为额定转速，r·min-1。

对于曲柄平衡的游梁式抽油机，曲柄轴净扭矩[8]为

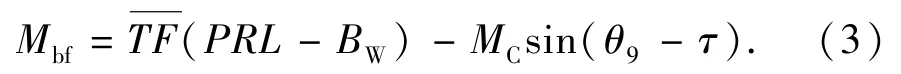
式中，为抽油机扭矩系数，m；PRL为悬点载荷，N；BW为结构不平衡重，N；MC为曲柄最大平衡扭矩，N·m；τ为曲柄平衡重偏置角，rad。

以抽油杆柱轴向振动的波动方程为基础，建立悬点载荷的仿真模型，具体模型参考文献[8]。

1.2 等效刚度和等效阻尼

1.2.1 带刚度与阻尼

根据图1(b)，皮带传动的力学模型简化为图2。图中，R1、R2分别为小带轮与大带轮半径，m；Lt为皮带切线段长度，m；Mf为大带轮阻力矩，N·m。

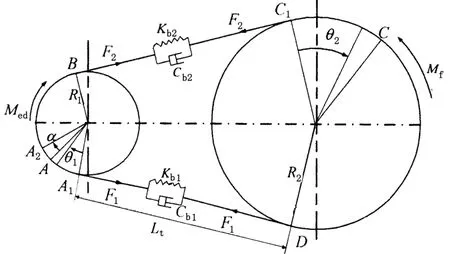
图2 带传动系统的力学模型Fig.2 Mechanical model of belt driving system

图2中，圆弧A1A、AB分别为任意时刻t小带轮静弧和动弧；圆弧C1C、CD分别为大带轮静弧和动弧。在静弧段带轮与皮带同速；在动弧段带轮与皮带之间存在相对滑动，其相对滑动速度随动弧段的圆周位置而变化[10]。将动弧段对应的圆周角αM定义为滑动角。目前在计算皮带紧边与松边的等效弹簧刚度系数Kb1、Kb2时，未考虑带轮滑动角对弹性刚度的影响，将等效刚度视为常数，并认为紧边与松边的刚度系数相等[11]：

式中，E为皮带材料的弹性模量，Pa；A为皮带横截面积，m2；Lt为皮带节线长度，m。

皮带传动系统带轮包角处的滑动角随着负载不断变化，导致皮带紧边和松边的长度随负载发生变化，进而影响皮带紧边与松边的等效刚度系数。当考虑带轮滑动角对皮带紧边与松边长度的影响时，皮带等效刚度系数计算公式为

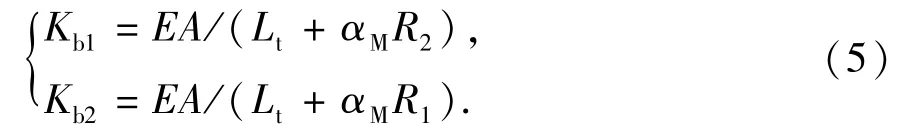
其中，滑动角αM由下式计算：

皮带传动系统等效阻尼由下式[11]计算：

式中，γ为阻尼系数，s/m。

1.2.2 传动轴等效扭转阻尼与等效扭转刚度

传动轴的等效扭转刚度为

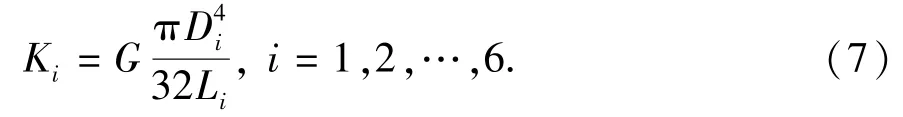
式中，G为材料切变模量，Pa；Li为计算轴段的长度，m。

传动轴扭转振动的等效阻尼主要是材料阻力，传动轴扭转阻尼[12-14]可表示为

式中，ζs为传动轴扭转阻尼比。

1.2.3 轮齿啮合刚度与啮合阻尼

考虑轮齿的弯曲变形、啮合点处的接触变形，根部剪切和轮齿弹性变形引起的啮合点的位移，用弹性力学方法，建立啮合齿副的啮合刚度为[12-13]

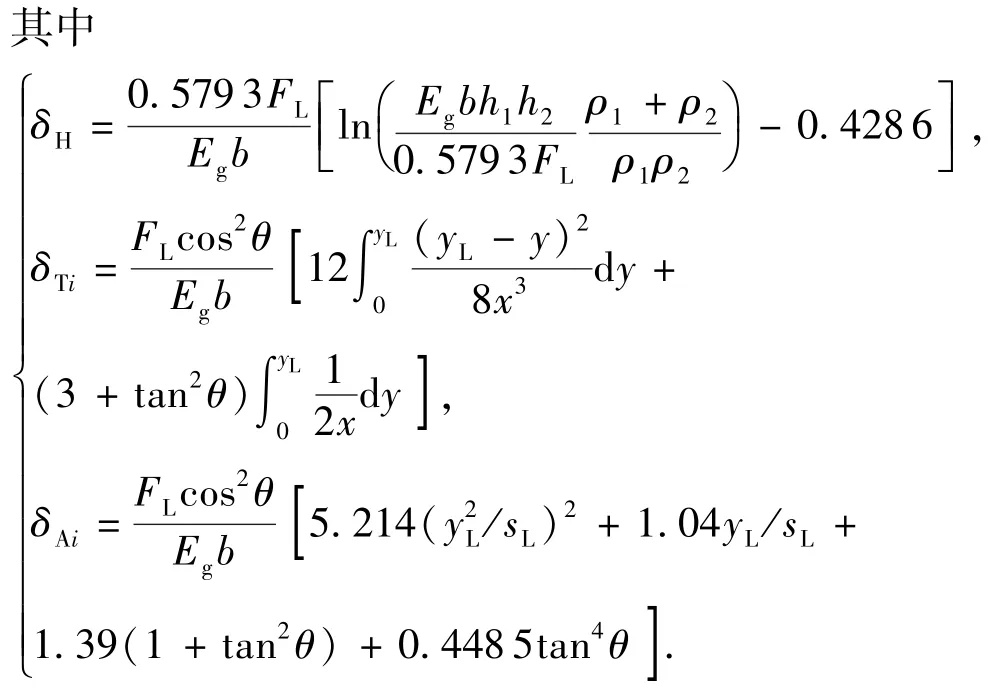
式中，FL为轮齿啮合法向分配载荷，N；δH为轮齿接触变形，m；δTi为轮齿弯曲及根部剪切引起的变形，m；δAi为轮齿弹性变形，m；Eg为轮齿材料弹性模量，Pa；b为齿轮齿宽，m；ρ为齿廓曲线曲率半径，m；hi、yL、sL、θ为齿轮几何尺寸；x、y为齿廓曲线坐标。

对于轮齿啮合时的载荷分配及啮合处的轮齿变形具体计算方法见文献[12]、[13]。

当考虑流体阻尼时，齿轮传动啮合阻尼为

轮齿的啮合阻尼计算公式[13-14]为

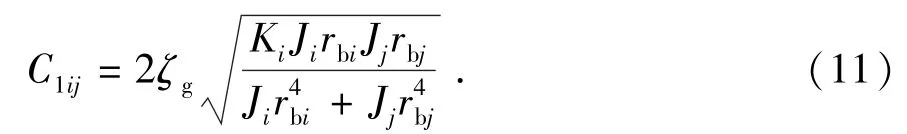
式中，ζg为轮齿啮合阻尼比。

考虑润滑油的影响，齿轮传动流体阻尼[13-16]为

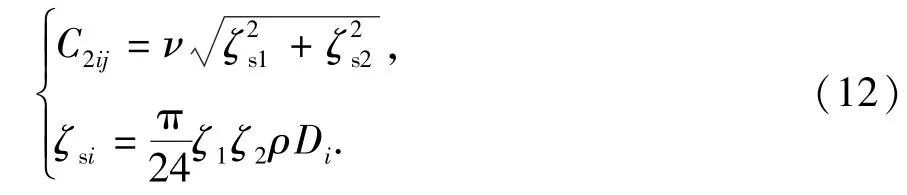
式中，ζ1为附加质量系数；ζ2为摩擦系数(根据润滑油匹配试验数据求得)；Di为相互啮合齿轮分度圆直径，m；ρ为润滑油密度，kg·m-3；ν为润滑油运动黏度，m2/s。

1.3 转动惯量计算

根据能量守恒原理将游梁式抽油机地面传动装置中悬点到曲柄的所有运动部件的转动惯量和质量转化到曲柄处，则等效转动惯量J9(10)为

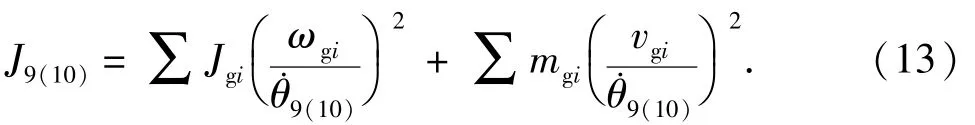
式中，Jgi、ωgi、vgi分别为摇杆机构中各机构转动惯量、角速度和速度。

2 仿真模型

2.1 系 统

游梁式抽油系统动力学仿真模型包括：描述皮带减速箱传动系统扭转振动的二阶常微分方程组和抽油杆柱轴向振动的波动方程。该模型是一个动力耦合的混合数学模型。将皮带减速箱传动系统微分方程(1)所示的二阶常微分方程组进行降阶，即简化为一阶常微分方程组，应用龙格库塔法建立地面常微分方程组数值积分形式的数值仿真模型；应用差分法建立抽油杆柱波动方程的数值仿真模型。并应用迭代法求解系统受迫振动响应，具体解法见文献[8]。

2.2 传动效率

建立系统各节点瞬时效率仿真模型、分析有杆抽油系统效率影响因素是进行有杆抽油机井能耗节点优化、系统故障诊断、提高系统效率的基础。皮带减速箱瞬时传动效率和平均传动效率分别为ηbg、ηA；皮带与减速箱的瞬时传动效率ηb、ηg的计算公式为

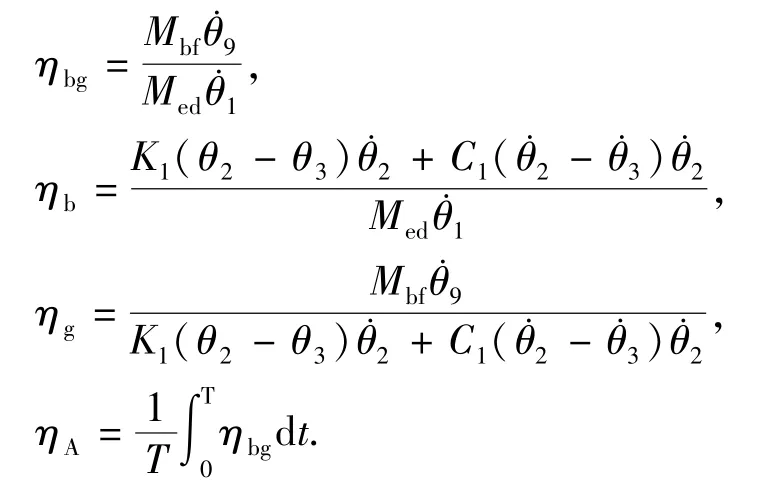
3 仿真实例及其分析

仿真计算的基本参数为：电动机额定功率PH=55 kW，额定转速nH=807 r/min，同步转速n0=1000 r/min；皮带长度L=4 m，单根皮带线密度ρ=0.37 kg/m；皮带根数z=4；单根皮带横截面积A=1.55×10-4m2；摩擦系数μ=0.6；小皮带轮直径D1=0.3 m；小皮带轮转动惯量J1=0.073 kg·m2；大皮带轮直径D2=0.9 m；大皮带轮转动惯量J2=1.13 kg·m2；第一根传动轴半径及长度为R23=0.056 94 m，R34=0.06175 m，L23=0.342 m，L34=0.536 m；第二根传动轴半径及长度为R57(R67)=0.088 5 m，L57(L67)=0.278 m；第三根传动轴半径及长度R89(R810)=0.11937 m，L89(L910)=1.205 m；第一根传动轴上的齿轮齿数z3(z4)=1，模数mn3(mn4)=0.006 m，齿宽b3(b4)=0.159 m，齿厚S3(S4)=0.0096 m，轮齿悬臂长度l3(l4)=0.009 m，齿根圆半径r3(r4)=0.062 m，转动惯量J3(J4)=0.25 kg·m2；第二根传动轴上的齿轮齿数z5(z6)=100，z7=19，模数mn5(mn6)=0.006 m，mn7=0.009 m，齿宽b5(b6)=0.159 m，b7=0.238 m，齿厚S5(S6)=0.0096 m，S7=0.0144 m，轮齿悬臂长度l5(l6)=0.008 16 m，l7=0.0135 m，齿根圆半径r5(r6)= 0.326 m，r7=0.091 m，转动惯量J5(J6)= 0.75 kg·m2，J7=2.75 kg·m2；第三根传动轴上齿轮齿数z8=102，模数mn8=0.009 m，齿宽b8=0.238 m，齿厚S8=0.0144 m，轮齿悬臂长度l8=0.01224 m，齿根圆半径r8=0.490 m，转动惯量J8=2.75 kg·m2；抽油机机构尺寸Rcyj=0.971772 1 m，Pcyj=2.602525 m，Ccyj=2 m，Kcyj=3.197813 m，Acyj=2.5 m，Icyj=1.861722 m。

3.1 系统动态特性

用单自由度等效曲柄仿真模型[8-9]和本文所建立的多自由扭转振动仿真模型进行对比仿真计算。图3给出了曲柄瞬时转速、扭矩、悬点示功图与皮带

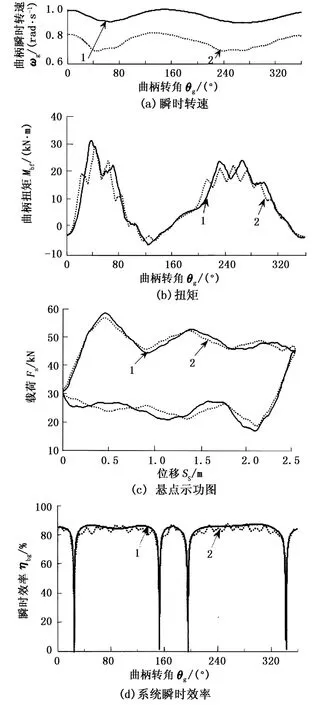
图3 系统动态参数仿真结果对比曲线Fig.3 Curves of comparison of dynamic parameters

减速箱瞬时传动效率的变化曲线(图中，箭头1指向单自由度等效曲柄模型仿真结果，箭头2指向多自由度扭转振动仿真结果)。

3.2 瞬时传动效率及影响因素分析

皮带减速箱瞬时传动效率仿真结果如图4所示。

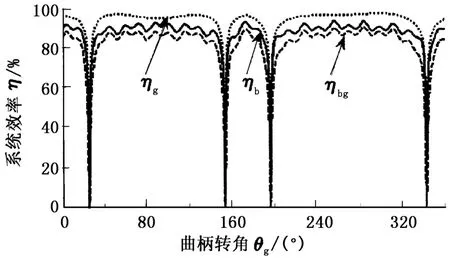
图4 瞬时传动效率变化规律Fig.4 Change rules of instantaneous efficiency of each node

图5给出了皮带减速箱平均传动效率随皮带预紧力、曲柄轴最大扭矩的变化规律。

图5 系统平均传动效率随皮带预紧力、曲柄最大负载扭矩变化规律Fig.5 Change of average transmission efficiency of system with initial tension of belt and maximum load torque of crank

由图5可知：①当皮带未打滑时，预紧力越大，皮带减速箱传动系统的平均传动效率越大；②皮带减速箱传动系统平均传动效率受负载扭矩最大值影响，曲柄扭矩最大值越大，平均传动效率越小。

4 结 论

(1)考虑地面传动装置的弹性时，曲柄扭矩、曲柄角速度波动明显，皮带减速箱瞬时传动效率不为常数，在进行游梁式抽油机地面传动装置动态仿真分析时，设定皮带减速箱传动效率为常数是不合理的。

(2)多自由度弹性系统扭转振动降低了系统传动效率，与减速箱传动系统扭转振动相比，皮带传动系统扭转振动对地面传动系统传动效率影响较大，进行多自由度弹性系统仿真分析是必要的。

(3)当负载扭矩幅值较小、皮带预紧力较大时，游梁式抽油机地面传动装置的传动效率较高；为此在油田实际操作中可通过合理配置抽汲参数降低负载扭矩幅值，增大皮带预紧力提高系统效率。

[1] 姚春东.提高抽油机井系统效率有效途径的计算机仿真分析[J].石油学报，2005，26(4)：106-110.YAO Chun-dong.Computer simulation for enhancing system efficiency of rod pumping well[J].Acta Petrolei Sinica，2005，26(4)：106-110.

[2] 冯国强，谢雄，韩岐清，等.抽油机井系统动态实时分析模型[J].中国石油大学学报：自然科学版，2010，34(4)：84-88.FENG Guo-qiang，XIE Xiong，HAN Qi-qing，et al.Real time analysis model of rod-pumped well system performance[J].Journal of China University of Petroleum(Edition of Natural Science)，2010，34(4)：84-88.

[3] 林日亿，孙茂盛，张邵东，等.有杆抽油泵沉没度的优化设计方法[J].石油大学学报：自然科学版，2005，29(4)：87-90.LIN Ri-yi，SUN Mao-sheng，ZHANG Shao-dong，et al.Optimization design method to determine submergence depth of sucker rod pump[J].Journal of the University of Petroleum，China(Edition of Natural Science)，2005，29(4)：87-90.

[4] 狄勤丰，王文昌，胡以宝，等.定向井抽油杆柱空间形态的计算方法[J].中国石油大学学报：自然科学版，2011，35(3)：72-75.DI Qin-feng，WANG Wen-chang，HU Yi-bao，et al.Calculation method of sucker rod strings space configuration in directional well[J].Journal of China University of Petroleum(Edition of Natural Science)，2011，35(3)：72-75.

[5] 王凯.定向井有杆抽油泵系统诊断模型的建立[J].中国石油大学学报：自然科学版，2010，34(2)：130-135.WANG Kai.Modeling method for fault diagnosis to sucker rod pumping system in directional well[J].Journal of China University of Petroleum(Edition of Natural Science)，2010，34(2)：130-135.

[6] 董世民，马德坤，李学丰.游梁式抽油系统动态参数仿真的综合数学模型[J].石油机械，2001(6)：46-48.DONG Shi-min，MA De-kun，LI Xue-feng.A comprehensive mathematical model for simulation of dynamic parameters of beam pumping system[J].China Petroleum Machinery，2001(6)：46-48.

[7] 吴晓东，李兆文，郜云飞，等.抽油机井系统数学仿真技术[J].石油学报，2000，21(5)：95-98.WU Xiao-dong，LI Zhao-wen，GAO Yun-fei，et al.Digital simulation technique of rod pumping system[J].Acta Petrolei Sinica，2000，21(5)：95-98.

[8] 董世民.抽油机井动态参数的计算机仿真与系统优化[M].北京：石油工业出版社，2003：52-72.

[9] 董世民，李海琴.抽油机井系统效率极限值的仿真研究[J].系统仿真学报，2008，20(13)：3533-3537.DONG Shi-min，LI Hai-qin.Simulating maximum of system efficiency of rod pumping wells[J].Journal of System Simulating，2008，20(13)：3533-3537.

[10] XU Jin-chao，LI Ju-hui，CHEN Jian，et al.Research on power saving positive torque and constant power pumping unit and tracking technique system[J].Procedia Engineering，2012(29)：1034-1041.

[11] 罗善明，余以道，郭迎福，等.带传动理论与新型带传动[M].北京：国防工业出版社，2006：62-78.

[12] 邵忍平.机械系统动力学[M].北京：机械工业出版社，2005：244-258.

[13] 李润方，王建军.齿轮系统动力学[M].北京：科学出版社，1996：154-188.

[14] ANDERSSON A，VEDMAR L.A dynamic model to determine vibrations in involute helical gears[J].Journal of Sound and Vibration，2003(260)：195-212.

[15] 綦耀光.二级分流式双圆弧齿轮减速箱结构特性对其振动性能的影响[J].石油大学学报：自然科学版，1998，22(6)：68-73.QI Yao-guang.Effects of structure parameters on the vibration behaviors of reducing box with two stage split flow Novikov gears of double circular arc tooth profiles[J].Journal of the University of Petroleum，China(Edition of Natural Science)，1998，22(6)：68-73.

[16] 曹宇光，张士华，刘海超，等.大型开式齿轮损伤强度数值模拟分析[J].中国石油大学学报：自然科学版，2012，36(5)：129-135.CAO Yu-guang，ZHANG Shi-hua，LIU Hai-chao，et al.Numerical simulation analysis of damages on strength of large-scale open gears[J].Journal of China University of Petroleum(Edition of Natural Science)，2012，36(5)：129-135.