三维油藏流动电位数值模拟及油水前缘预测

卜亚辉,姚 军,李爱芬,刘均荣,于伟强

(中国石油大学石油工程学院,山东青岛266580)

流动电位效应是一种广泛存在于油气田开发过程中的耦合流动现象，因具有反映地层及流体性质的能力而受地球物理界关注[1-4]，特别是油水两相流动时其前缘位置具有显著的流动电位效应，对该效应的测量解释可以实现前缘位置的预测。前人对油气田开发过程中电位耦合系数的变化进行了研究和测量[5-9]。由于油田开发过程中的流动电位信号伴随地层流体运动而产生因而具有低压直流的特点，采用常规测井工具可以获得较高精度的观测值[10-13]。笔者从耦合流动的基本原理出发，建立电场和渗流场的耦合模型并采用有限差分方法求解，模拟计算油藏生产过程中的井底电位变化响应，分析电位随油水前缘位置的变化规律。

1 基本原理

1.1 流动电位

流动电位的产生与岩石表面的带电现象有关，通常砂岩油藏表面带负电。当电解质溶液存在时，固液界面上会形成“双电子层”[14]，该结构中“扩散层”中的离子能够随流体迁移。如图1所示，当电解质溶液沿压力差(Δp)方向流动时，扩散层中的电荷发生定向移动形成流动电流 (Js)及流动电位(ΔU)；与此同时，远离固液界面的电荷在该电位驱动下将产生移动，形成传导电流(Jc)。当外加电源为零时，两个电流相互抵消维持整体电中性，流动电流可以看作传导电流的电源，虽然该电源只产生在储层区域，但传导电流能够穿越储层延伸到更远的空间范围。

图1 流动电流和传导电流示意图Fig.1 Sketch map of streaming current and conduct current

1.2 耦合流动理论

耦合流动理论是在非平衡热力学条件下提出的，假设流量qi与其驱动力Xi呈线性关系，

式(1)耦合现象的关系式称为“翁萨格倒易关系”(Onsager's reciprocal relation)，其中Lij称为耦合系数，具有对称的性质(Lij=Lji)，常见的流量和对应驱动力包括电流与电场梯度、液体流量与液体压力梯度、浓度流量和浓度梯度、热流量和温度梯度。

流动电位是渗流场与电流场之间的耦合问题，其关系可用线性方程组描述，即

式中，q1为液体的流速，对应的作用力X1等于压力梯度▽p；q2为电流密度，对应的作用力X2等于电压梯度▽U。

当不考虑耦合效应时(Lij=0)，式(2)可分别简化为达西定律和欧姆定律方程，L11=-kμ-1，L22=-σ，于是式(2)变为

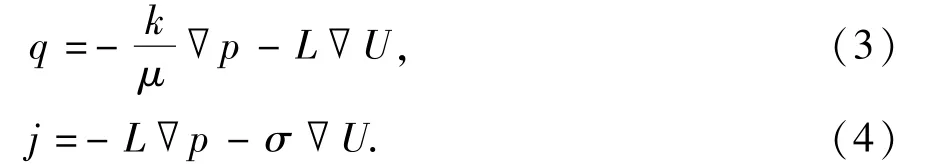
式中，q为流速，m·s-1；k为岩石的渗透率，m2；μ为流体黏度，Pa·s；p为压力，Pa；j为电流密度，A·m-2；U为电位，V；L为流动电流耦合系数，A·m-1·Pa-1；σ为岩石饱和地层流体时的电导率，S·m-1。

式(3)等号右边第二项可以看作电流对渗流的回馈作用，Fitterman等[15]研究认为，油藏条件下这种回馈作用影响很小可以忽略，因此该耦合问题简化为渗流产生电流的单向过程。此外，相比压力波较慢的传播速度，电位会在极短时间内达到平衡状态，电流问题可以按照稳态进行处理，从而耦合问题的求解得到简化。

当没有外加电源时，即▽·j=0，式(4)变为

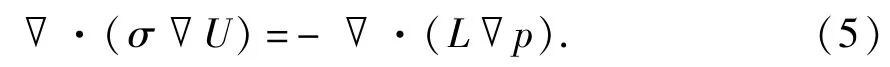
将式(5)等号右边看作电源项，用qe(x，y，z)表示，则有

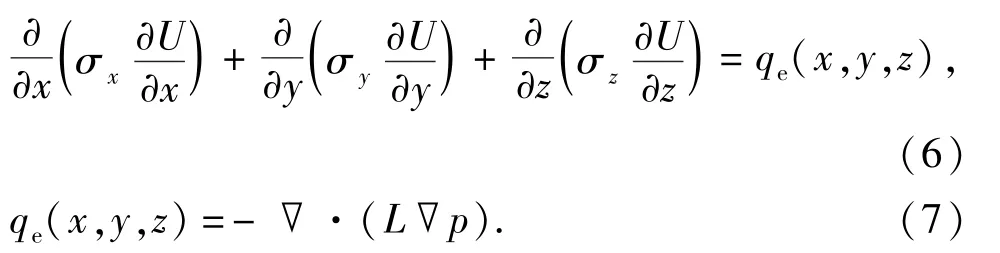
其中，σx、σy和σz是同一位置3个方向上的电导率，反映饱和流体岩石电导率的各向异性。以上方程组可按Sill[16]提出的方法进行求解：首先求解渗流问题，得到压力和饱和度的分布；其次代入方程(7)求解电源项qe(x，y，z)的位置和大小；最后求解电流方程(6)得到整个模型中的电位分布。电流问题的求解与渗流问题具有相似性，本文中采用的是有限差分方法。

图2为直角坐标下离散后的网格单元及其参数。网格单元3个方向上的尺寸为Δx、Δy和Δz；图2(a)中x方向上通过左右两个侧面的流量分别为，y方向上的流量为和，z方向上为；孔隙度φi，j，k、渗透率ki，j，k和压力pi，j，k定义在网格单元的中心；图2(b)中，x方向上两个面上的电流密度为和，y方向上为，z方向上为；饱和流体的岩石电导率σi，j，k、流动电流耦合系数Li，j，k和电位Ui，j，k定义在网格单元的中心，则式(6)三维不等距网格有限差分格式为

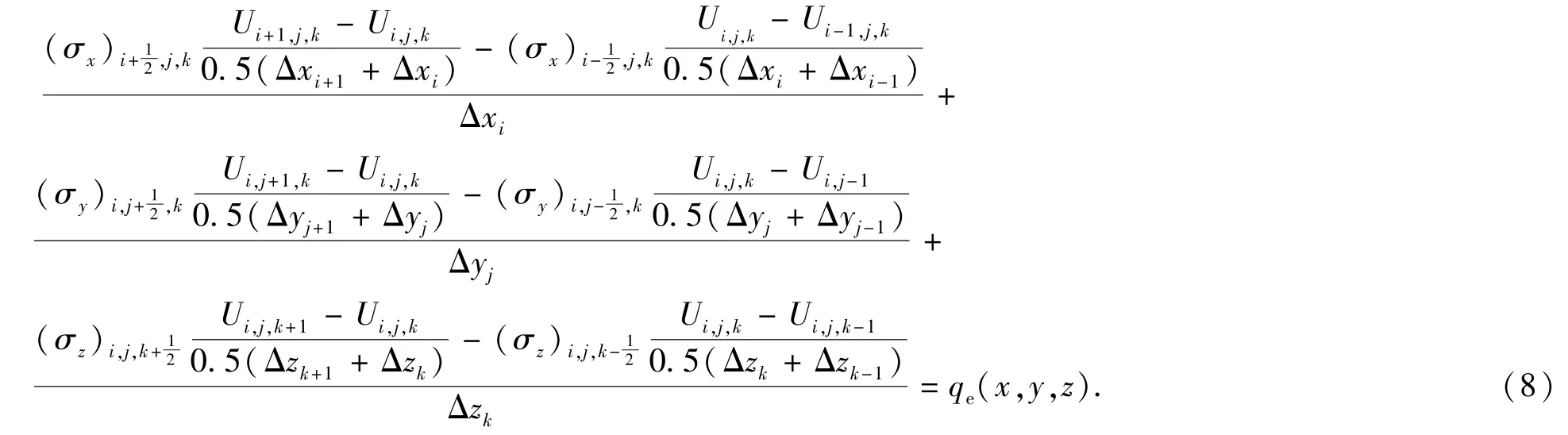
其中，网格单元x方向上两侧面位置的电导率分别为，其他方向上表示方法相同。

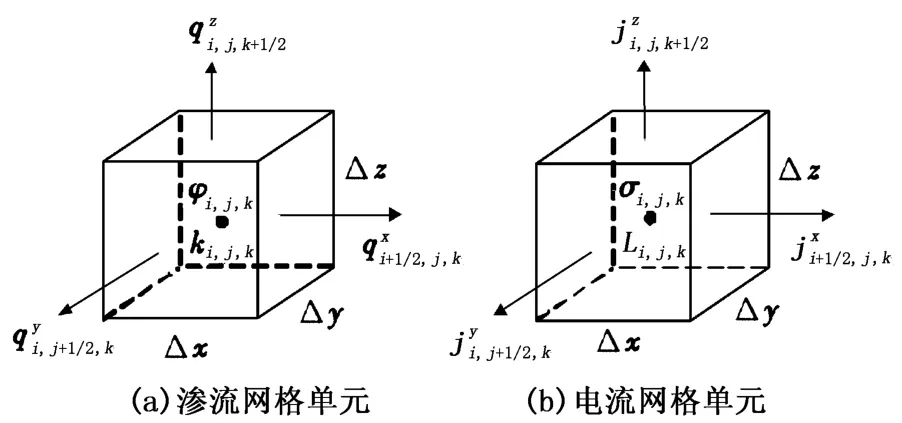
图2 网格单元中流体及电学参数示意图Fig.2 Sketch map of hydraulic and electrical parameters in grid cell

求解过程的关键是确定电流源位置，通过理论推导说明电流源的位置，将电流源qe展开可得

将达西方程代入▽·q展开后可得

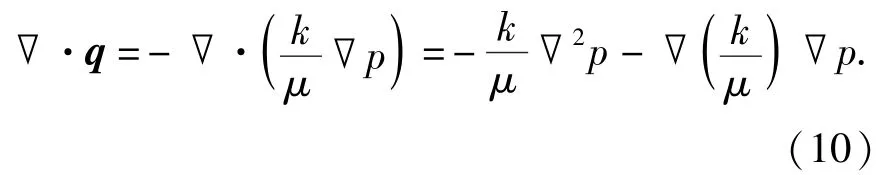
式(10)整理可得

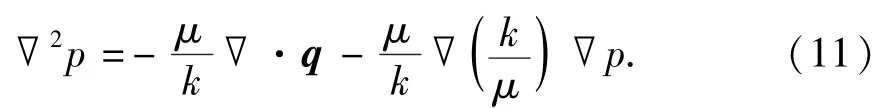
将(11)代入式(9)得

式(12)中等号右边的3项分别代表：第一项来自▽·q，即流体源汇处，通常是注入井或生产井所在位置，该项只在近井处影响显著，且稳定生产时电位的空间分布不随时间变化；第二项来自▽(kμ-1)▽p，即地层性质有明显变化的地方，比如裂缝或断层；第三项来自▽L▽p，由于电流耦合系数L=σ(Sw)Cv(Sw)与含水饱和度Sw有关，而油水两相流动时Sw随时间改变，特别是油水交界面变化显著，这是通过流动电位预测油水前缘位置的物理基础。

2 三维流动电位数值模拟

2.1 模型及参数

数值模型如图3所示。模型分为油藏区域和扩展区域两部分，油水渗流只发生在油藏区域，而电流能够穿过油藏边界向更广阔的空间传播，扩展区域代表了油藏的盖层、底层和周围封闭油藏的岩层。模型尺寸为3 km×3 km×1 km，网格数为100×100×25，零电位参考点选在边界角，油藏尺寸为300 m×300 m×15 m，网格数为50×50×7，油藏顶面埋藏深度500 m。油藏区域采用等距网格，扩展区域的网格尺寸呈等比递增，越靠近油藏区域网格越密。

图3 数值模型示意图Fig.3 Sketch map of numerical model

油藏参数：孔隙度为0.25，平面渗透率为0.4 μm2，垂向渗透率为0.02 μm2；考虑地层非均质性油层中部有渗透率为0.6 μm2的高渗层夹层；束缚水饱和度为0.2，残余油饱和度为0.2；地层条件下原油黏度为5 mPa·s，地层水黏度为1 mPa·s；原始地层压力为14 MPa；地层水电导率为0.118 S·m-1，原油电导率为1×10-5S·m-1；外部扩展区域假设被均质泥页岩包裹，其电导率为1×10-3S·m-1；流动电位耦合系数采用文献[12]中砂岩岩心测量值2.7×10-7V·Pa-1。以四分之一“五点法”井网为对象，注水井和生产井各1口分别位于油藏对角位置，生产井定产液量120 m3·d-1，注水井定井底压力17 MPa，模拟生产3 600 d。渗流问题使用Eclipse求解，获取其压力场和饱和度场作为电流问题的已知条件，使用Fortran编写的有限差分程序求解电位分布[17]。

2.2 模拟结果

x-y平面电位U和含油饱和度So模拟结果如图4所示。随着注入水沿对角方向向生产井推进，油水前缘位置出现了高电位区域，且该区域的形态与油水前缘的形态基本一致。对比图5沿I1井到P1井连线上的电位分布，生产120 d时电位的最大值8 mV出现在注水井附近，随后其绝对值逐渐变小，但注水井底的电位与前缘位置依然保持5 mV的电位差；1200 d时电位开始增大，此时注入水已经波及到了油藏二分之一的区域，前缘位置的流速开始加快；3000 d时前缘电位高出注水井底电位近30 mV。该变化过程的原因是越靠近井底流体的压力梯度越大，油水前缘的电源效应越强。从单条曲线形态来看，峰值右侧的曲线相对平缓，而左侧电位下降更加剧烈，这是因为以油水过渡带为界，两侧流体的电学性质存在明显差异，水相电导率远大于油相的；2 000 d的曲线末端出现先下降后上升的形态，因为此时受到油水前缘和生产井两个电源的影响，且两源的影响作用大致相等，其后则前者逐渐占据优势。

图4 x-y平面电位U和含油饱和度So模拟结果Fig.4 Electrical potential and oil saturation distribution plot in x-y plane

图5 沿I1井到P1井连线的电位模拟结果(I1 0 m，P1 420 m)Fig.5 Electrical potential distribution along diagonal line of I1 to P1(I1 0 m，P1 420 m)

图6为沿I1井到P1井连线的电位剖面。受中部高渗透层影响，注入水沿该层快速推进，该层高电位区域较其他层位更接近生产井。1 200 d时电位绝对值最小，其后电位开始出现上升趋势。

如图7，如果在垂直方向沿井壁取出各层的电位，120 d时生产井井底电位呈一条直线，480 d开始出现变化，中部高渗透层出现明显电位异常，其差值约为5 mV，随后电位差距更加明显，最大差值可超过20 mV。地层非均质性在注水井井底也有反映，该电位曲线也出现向高渗透层弯曲的形态，电位差异超过10 mV。

图7中注水井井底电位呈现较为复杂的变化过程，1200 d之前逐渐降低，1200 d以后逐渐增大，这是油水前缘电源信号的特征决定的。由式(12)第三项▽L▽p可知，电源值不仅取决于两个梯度模的大小，还取决与二者之间的夹角，1 200 d时注入水波及到油藏约一半的区域，此时前缘位置的水相流速减慢，电源的强度也减弱。同时随着油水前缘向生产井移动，电源距注水井越来越远，该位置接收到的信号强度减弱，所以井底位置的电位信号响应是油水前缘信号源强度和距离两因素的综合结果，解释过程中需要注意区分判别。

图6 沿I1井到P1井连线剖面的电位U和含油饱和度So模拟结果Fig.6 Electrical potential and oil saturation distribution plot along I1-P1 diagonal section

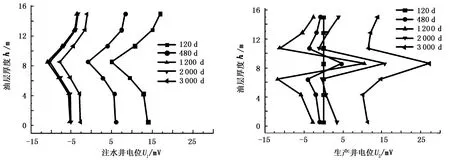
图7 沿井壁方向电位分布曲线Fig.7 Electrical potential distribution along borehole wall

如果以含水饱和度0.5为边界标记油水前缘位置，井底电位与油水前缘的位置关系如图8所示。对于 I1井，当距离280 m时电位值约为3 mV，随后开始缓慢下降，到150 m时电位趋于平稳保持在-10 mV，当油水前缘接近P1井约10 m时开始上升；对于P1井，生产前期电位始终保持在0 mV，当距离75 m时电位开始明显变化，说明通过对生产井井底的电位连续测量有可能实现远距离预测油水前缘的位置。根据文献[8]，油藏实测的环境噪声界限是0.1 mV，即该信号之下的电位测量值不可解释，若以该值为判断标准，模拟结果的预测距离是107 m，即使以5 mV为下界，该距离也能够达到48 m，说明该方法理论上具有远距离预测油水前缘位置的能力。以上研究主要针对均质模型，对于非均质模型，油水前缘将呈现更加复杂的形态，通过多个测点的观测值可以实现其位置的预测。

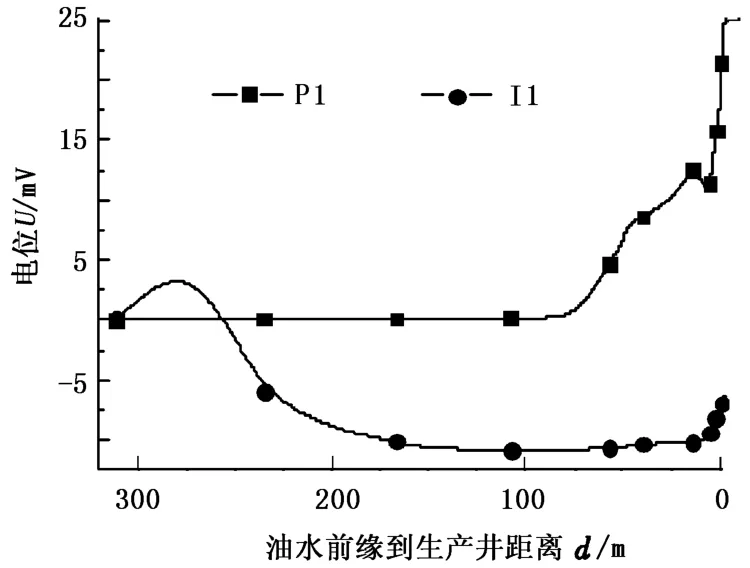
图8 井底电位与油水前缘到生产井距离的关系Fig.8 Plot of electrical potential in borehole with oil-water front distance to production well

3 结论及建议

(1)高电位出现在油水前缘位置并随着注入水向生产井推进，生产井井底电位曲线显示油水前缘距生产井75 m时即可被识别，因而具备远距离识别油水前缘的能力。

(2)注入水沿高渗透层的快速前进会引起明显的电位异常，注水井底电位差异约5 mV，生产井底电位差异约15 mV，最大值出现在高渗层所在位置，所以沿井壁布置的多个电极测量数据可以评价地层非均质性及注入水的不均匀推进。

(3)油水前缘越接近生产井，电位异常信号越明显，一方面是由于电源位置不断向生产井接近，另一方面因为越靠近井底压力梯度越大，电源的作用越强，所以储层渗透率越小、油井产量越大、油水性质差异越明显时，该方法的应用可行性越大。

[1] 杨春梅，李洪奇，陆大卫，等.油田开发过程中的动电现象研究[J].地球物理学展，2005，20(4)：1140-1144.YANG Chun-mei，LI Hong-qi，LU Da-wei，et al.Electrokinetic phenomena in oilfield development[J].Progress in Geophysics，2005，20(4)：1140-1144.

[2] 牛建军，张晓培，杜立志.稠油汽驱电位法动态监测技术[J].吉林大学学报：地球科学版，2008，38(5)：887-891.NIU Jian-jun，ZHANG Xiao-pei，DU Li-zhi.The potential monitoring technique during inject steam to drive thick oil[J].Journal of Jilin University(Earth Science E-dition)，2008，38(5)：887-891.

[3] 丁次乾.矿场地球物理[M].东营：石油大学出版社，2002.

[4] MITCHELL J K.Conduction phenomena：from theory to geotechnical practice[J].Geotechnique，1991，3(3)：299-340.

[5] GUICHET X，JOUNIAUX L，POZZI J P.Streaming potential of a sand column in partial saturation conditions[J].Journal of Geophysical Research，2003，108(B3)：2141.

[6] REVIL A，LINDE N，CEREPI A，et al.Electrokinetic coupling in unsaturated porous media[J].Journal of Colloid and Interface Science，2007，313(1)：315-327.

[7] GLOVER P W J，NICHOLAS D.Streaming potential coupling coefficient of quartz glass bead packs：dependence on grain diameter，pore size，and pore throat radius[J].Geophysics，2010，75(6)：F225-241.

[8] ALLEGRE V，JOUNIAUX L，LEHMANN F，et al.Streaming potential dependence on water-content in Fontainebleau sand[J].2010，182：1248-1266.

[9] VINOGRADOV J，JACKSON M D.Multiphase streaming potential in sandstones saturated with gas/brine and oil/brine during drainage and imbibition[J].Geophys Res Lett，2011，38(1)：L01301.

[10] WURMSTICH B，MORGAN F D.Modeling of streaming potential responses caused by oil well pumping[J].Geophysics，1994，59(1)：46-56.

[11] CHEN M Y，RAGHURAMAN B，BRYANT I D.Streaming potential applications in oil fields[R].SPE 102106，2006.

[12] SAUNDERS J H，JACKSON M D，PAIN C C.Fluid flow monitoring in oilfields using downhole measurements of electrokinetic potential[J].Geophysics，2008，73(5)：E165-180.

[13] JACKSON M D，GUIAMALI M Y.Real-time measurements of spontaneous potential for inflow monitoring in intelligent wells[R].SPE 135146，2010.

[14] 赵福麟.EOR原理[M].东营：石油大学出版社，2000.

[15] FITTERMAN D V.Electrokinetic and magnetic anomalies associated with dilatant regions in a layered earth[J].J Geophys Res，1978，83：5293-5928.

[16] SILL W R.Self-potential modeling from primary flows[J].Geophysics，1983，48(1)：73-46.

[17] 倪光正.工程电磁场数值计算[M].2版.北京：机械工业出版社，2010.