振动条件下机载合成孔径激光雷达成像处理
马 萌 李道京 杜剑波③①(中国科学院电子学研究所 北京 100190)(微波成像技术重点实验室 北京 100190)
③(中国科学院大学 北京 100049)
振动条件下机载合成孔径激光雷达成像处理
马 萌*①②③李道京①②杜剑波①②③①(中国科学院电子学研究所 北京 100190)②(微波成像技术重点实验室 北京 100190)
③(中国科学院大学 北京 100049)
该文研究了单探测器和顺轨双探测器机载合成孔径激光雷达在振动条件下的成像处理问题。根据平台振动在短时间内对成像影响小的特点,基于单探测器激光雷达研究了子孔径成像与相位梯度自聚焦相结合的成像处理方法。为获得方位向长条带图像,分别使用了条带相位梯度自聚焦方法和基于多普勒中心频率估计的子孔径图像拼接方法,并分析比较了二者的性能。针对单探测器激光雷达的不足,提出了基于顺轨双探测器干涉处理的振动相位误差估计与补偿方法。仿真分析结果验证了该文方法的有效性。
激光雷达;合成孔径;成像处理;载机振动
1 引言
合成孔径激光雷达(Synthetic Aperture Ladar, SAL)为激光雷达实现远距离高分率成像提供了可能,在军事侦察与空间探测方面具有重要的应用潜力。目前,国内外关于SAL的相关理论研究与试验工作已广泛展开[1-4],其中以2011年美国洛克希德马丁公司的机载SAL飞行试验最具代表性[4]。该次试验对距离1.6 km的地面目标实现了幅宽1 m,分辨率优于3.3 cm的成像。
机载SAL工作在光学频段,相比微波合成孔径雷达(Synthetic Aperture Radar, SAR)波长较短,使其具有短时间获得高分辨率图像的可能性,但与之相对应,载机平台的微小振动都会引起信号相位的显著变化,这给机载SAL成像处理带来许多困难。
为抑制载机平台振动带来的影响,国内外开展了广泛的研究。文献[5,6]主要分析了振动对成像的影响,文献[7,8]提出了对振动估计与抑制的方法。值得注意的是,洛克希德马丁公司在飞行样机的设计中特别明确了减振器的作用,同时在成像处理中采用了微波 SAR常用的相位梯度自聚焦(Phase Gradient Autofocus, PGA)方法来进一步抑制振动的影响。受其启发,文献[9]分析了机载SAL关键技术和实现方案,提出了使用稳定平台(包括磁悬浮稳定平台)来初步抑制载机振动的思路。
本文是文献[9]工作的继续,主要内容包括:从方位频谱角度分析了平台振动对回波信号的影响;在单探测器情况下,为解决子孔径PGA处理后无法获得长条带图像的问题,借鉴了条带相位梯度自聚焦(Stripmap Phase Gradient Autofocus, SPGA)方法,并研究了基于多普勒中心频率估计的图像拼接方法;针对单探测器的不足,研究了顺轨双探测器情况下利用干涉相位对振动引起的相位误差进行估计与补偿的方法;通过仿真,对以上方法进行验证。
2 振动对回波信号的影响
为抑制载机振动对成像的影响,首先需考虑将机载SAL安装在稳定平台上。目前的机载稳定平台能够将振动限制在幅度小于20 μm,频率低于50 Hz的范围内。在此条件下,由振动产生的激光信号多普勒频率范围可控制在10 kHz以内,故使用稳定平台对机载SAL高分辨率成像具有重要意义。即便如此,对于波长在1 μm数量级的激光而言,由平台振动造成的相位误差能达到100 rad数量级,使图像在方位向严重散焦[6]。下面以正侧视工作模式为例,对平台振动的影响进行分析。正侧视工作模式的成像几何模型如图1所示。其中,tk代表慢时间,P为地面目标散射点,飞机平台速度为V, α为激光入射角,H0为平台飞行高度,x0为零多普勒位置时斜距在X轴的投影。
由于激光以光速传播,可认为在信号发射与接收过程中平台振动保持不变,即振动仅随慢时间变化。将振动在3维坐标系下进行分解:X (tk),Y(tk), Z(tk)。则飞机平台相对于目标点P的斜距历程为:

图1 正侧视机载SAL成像几何模型Fig. 1 Geometric model of side-looking airborne SAL imaging

其中R0为零多普勒位置处的斜距,RV(tk)是由于振动引起的斜距:

观察式(3),发现前两项与传统的SAR的斜距相同,而第3项是由振动引起的,对其进行分析。假设各个分量的振动均为正弦振动,且在稳定平台的限制下其振幅小于20 μm。对式(3)第3项进行近似处理,只保留能够引起回波相位显著变化的项(与激光波长λ能够比拟的项)得到:

对于SAL,由于束散角较小,通常在毫弧度量级,全孔径长度远小于零多普勒位置处斜距,因此可忽略上式分子中的第2项,得到斜距的表达式为:

可见,实际对信号相位产生影响的主要是X轴和Z轴 方 向 上 的 振 动 。 现 另δR(tk)=(x0X(tk)+H0Z(tk))/R0,则式(5)可进一步简化:

值得注意的是,由于束散角较小,同一时刻对于波束覆盖区域内的所有目标散射点,可认为斜距上振动带来的影响是相同的[10];而且由振动引起的距离向位置变化远小于距离向采样间隔,因此不会产生距离走动。根据斜距表达式,可计算回波信号的多普勒相位:

其中 ϕr(tk)和 ϕe(tk)分别为SAL平台匀速直线运动产生的多普勒相位和由振动产生的多普勒相位:

由此获得方位向的信号模型(不考虑距离向):

A0是与慢时间无关的幅度值。则回波信号的方位向频谱为:

其中,Hr(fd)和 He(fd)分别对应式(9)中两个指数项的傅里叶变换。
从式(10)可以看到,实际回波的频谱为理想回波频谱与振动信号频谱的卷积。由于激光波长短的特点,振动信号的微小变化都会显著提高其频谱带宽,对回波信号的方位谱进行调制,增加成像难度。因此,限制振动信号的频谱带宽对成像尤为重要。
由于SAL合成孔径时间较短,可对振动作进一步假设,认为其在短成像时间内为单频正弦振动,且频率稳定,因此可认为振动产生的斜距变化具有单频正弦信号的形式,设其为:

其中A为振动幅度,fV为振动频率,ϕV为振动的初相位。则由振动引起的相位误差为:

根据式(12)可计算出振动引起的瞬时多普勒频率为:

这与振动的瞬时速度δVr(tk)=2πfVA cos(2πfVtk+ϕV)成正比。可见,决定振动信号方谱带宽的因素是成像时间内振动瞬时速度的变化范围。所以,在实际成像中,应考虑限制振动瞬时速度变化范围,以减小其带宽。
3 单探测器机载SAL成像处理
根据第2节的分析,限制成像时间内振动信号的频谱带宽是减少振动对SAL成像影响的关键。文献[9]中提到,由于激光波长较短,SAL系统在短合成孔径时间内即可获得足够大的方位带宽,以满足高分辨率的系统设计。这使得SAL在慢时间域的子孔径成像成为可能。同时,受到稳定平台的限制,平台振动的频率有限,在子孔径时间内振动的瞬时速度变化较小,振动信号产生的方位带宽相比全孔径时间被大大削减。因此,对于单探测器SAL系统可采用子孔径结合PGA的方法进行成像处理,以减少成像时间来限制振动信号带宽。
PGA算法最早由文献[11]提出,广泛应用于微波 SAR自聚焦中。该方法不基于模型,可鲁棒地依靠图像中的强点进行相位误差估计,其主要分为圆周移位、加窗、相位估计和相位补偿迭代4个步骤。其中的圆周移位操作是为了补偿强点的线性相位,然而在实际处理中,由于目标点散焦严重,圆周移位后仍残余有线性相位,该项会对相位估计产生影响,使PGA无法准确估计线性相位误差。
由于PGA无法准确估计线性相位,甚至会引入新的线性相位误差,子孔径成像结果在方位向会存在位置偏移,这给获得长条带图像带来困难。这里,考虑使用SPGA来解决该问题。文献[12]给出了一种基于相位梯度拼接的SPGA方法,该方法利用图像中的强点估计出该点所在合成孔径的相位误差梯度,然后使用相邻强点间合成孔径重复区域的相位梯度信息进行相位梯度的拼接,从而得到整个方位向的相位梯度,进而估计出全方位向相位误差。该方法相当于每次迭代都是对整个方位向的数据进行相位补偿,由于补偿相位连续,保证了图像相对几何位置的准确性。
借鉴上述方法,可对SAL信号在慢时间域划分子孔径,对各个子孔径进行PGA处理,估计相位误差梯度。为实现子孔径相位梯度的拼接,相邻子孔径间应设有一定的重复数据。使用该方法可获得全孔径成像结果,但由于PGA无法完全准确估计相位误差,且激光频段下由目标几何形状引起的相干斑严重,使得图像实际分辨率无法达到全孔径成像的理论值。为抑制振动和相干斑的影响,可在多普勒域重新划分频域子孔径,进行多视处理。整个成像方法的流程图如图2(a)所示。
当成像场景中无明显强点的时候,经PGA处理后的图像仍残存有较大的相位误差,此时采用上述的成像方法,在进行多视处理时得到的频域子孔径图像在方位向仍有几何位置错位,这使得非相干叠加后的图像分辨率进一步降低。而且,上述成像方法在时域和频域都划分子孔径,步骤较为繁琐,成像效率不高。本文研究了基于多普勒中心频率估计的图像拼接方法来获得方位向长条带图像。
对于时域子孔径PGA处理后的图像,在高阶(2阶及以上)相位误差完全补偿的假设下,可认为图像仅残存有1阶线性误差,该相位误差在方位频谱上表现为频谱搬移。因此,对子孔径进行多普勒中心频率估计,并将其频谱搬移到零频位置即相当于补偿了残存的线性相位误差。对频谱搬移后的各个子孔径进行成像,然后根据子孔径中心时刻对应的几何位置可对图像进行多视拼接,这与频谱分析(SPECtral ANalysis, SPECAN)成像算法[13]后期的图像多视拼接类似。同样,该方法需要对子孔径图像进行有效成像区域的选取。需要注意的是,经过PGA处理后的数据相位信息发生改变,无法使用基于相位的多普勒中心估计方法。该成像方法的流程图见图2(b)。
比较上述两种方法,二者的主要区别体现在对PGA无法估计线性相位的解决方法不同:SPGA法利用子孔径间的重叠数据,进行相位梯度拼接,实际上是将各个子孔径间的线性相位误差一致化;而图像拼接法则假设PGA对各个子孔径的高阶相位误差补偿效果一致,利用多普勒中心频率搬移补偿残余的线性相位误差。在成像效率方面,图像拼接法多视成像效率较高,若使用非迭代的优质 PGA (Quality Phase Gradient Autofocus, QPGA)[14]有望进行快视处理,充分发挥SAL短时成像的优点。然而,SPGA法能够得到相位连续的全孔径图像,而图像拼接法获得相位连续的全孔径图像较为复杂[13]。因此,在实际应用中应综合考虑场景条件和应用需求,在二者中选择合适的方法进行成像处理。

图2 两种方法的流程图Fig. 2 Flow diagram of the two methods
4 顺轨双探测器机载SAL成像处理
单探测器下的成像方法主要依赖PGA对振动相位误差进行估计与补偿,当场景中缺少孤立强点时,PGA效果会受到限制,影响相位误差估计的准确性。针对这一问题,本文考虑将微波 SAR中的顺轨干涉对运动目标的测速技术引入到机载 SAL系统中,利用顺轨干涉相位对振动引起的相位误差进行估计,在补偿相位误差后采用PGA进一步提高图像质量。
4.1 顺轨干涉测速原理
微波 SAR中的顺轨干涉技术主要是利用在顺轨方向设置两个或多个探测器来实现对场景中运动目标径向速度的测量。典型的一发两收顺轨干涉测速原理图如图3所示。
在顺轨方向依次安置信号接收单元R1,发射单元T和接收单元R2。由T发射信号,R1和R2同时接收信号,这样可在C1与C2处形成两个等效相位中心。两个接收单元的间隔即为基线长度d。这样的观测结构,可实现同一时刻在不同空间位置对同一场景进行观测;也可等效看作延时Δt后(tk+Δt时刻C1到达tk时刻时C2的位置),在同一空间位置对同一场景进行了两次观测。由于在Δt时间内运动目标位置发生改变,造成回波信号相位变化,对两路接收单元信号的成像结果进行干涉处理,即可对目标的径向速度Vr进行估计。目标径向速度的估计方程[15]为:

其中Δϕ为干涉相位,λ为载波波长,V为平台速度。

图3 顺轨干涉测速原理图Fig. 3 Schematic diagram of velocity estimation using along-track interferometry
在实际飞行中,难以保证延时Δt为脉冲重复时间的整数倍,通常作法是在多普勒域对某个接收单元的接收信号进行相位补偿,以达到时域延时目的[16]。在基线长度较短,由视差引起的多普勒频率差较小的情况下,可近似认为多普勒域相位补偿后的信号即为实际延时信号。
受到相位以2π为周期的影响,可检测的最大不模糊径向速度为:

因此在设计基线时应考虑目标的最大径向速度。
4.2 振动相位误差估计与补偿
对于机载SAL系统,上述的双探测器结构可以利用光纤阵列实现。2012年,美国学者Crouch进行了交轨双探测器桌面SAL系统的干涉测高试验,成功获得了目标的干涉相位图并得到了一枚硬币的高程信息[17,18]。其中文献[18]提到了使用光纤阵列进行单航过干涉试验,其实验结果表明了机载SAL系统利用光纤阵列实现顺轨双探测器提取干涉相位具有可行性。
机载SAL系统中的平台振动,可等效为平台稳定飞行而目标处于振动状态。利用稳定平台把振动频率限制在一定范围内,此时进行慢时间域子孔径划分,可把子孔径时间内的振动近似为匀速直线运动。对各个子孔径进行成像,提取干涉相位信息估计出振动速度。由振动速度和慢时间可计算出振动产生的斜距:
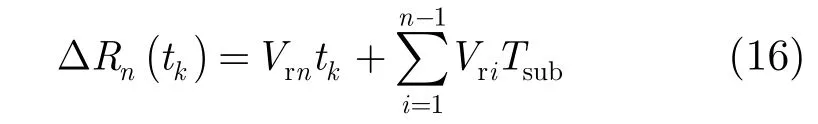
其中δ Rn(tk)为第n个子孔径振动产生的斜距,Vrn表示第n个子孔径估计的振动速度,Tsub为子孔径时间长度。这里将初始斜距设为 0,不会影响相位误差补偿。得到振动产生的斜距后即可由式(12)对回波数据进行相位补偿。由于子孔径成像结果受到振动影响,会使提取的干涉相位不准确,在处理过程中可选取相干系数高的区域提取相位信息。
利用该方法估计振动速度相当于是对振动瞬时速度进行时域采样,采样间隔为子孔径时间Tsub。为满足 Nyquist采样定理,选择的Tsub应满足1/Tsub≥ 2fVmax, fVmax为振动可达到的最高频率。而实际中,为得到更为精确的振动相位误差,Tsub可尽量选取较小的值,这样也可以减少振动对子孔径成像的影响,得到更为准确的干涉相位。受到最大不模糊速度的限制,基线长度应能够满足对振动最大瞬时速度的测量。
由于无法提取准确的干涉相位和对振动在子孔径内作匀速直线运动的近似,利用干涉测速估计的相位误差仍不精确,因此在相位误差粗补偿后,可使用PGA进一步对残余的相位误差进行估计补偿。此时,大部分相位误差已被粗补偿掉,故可直接对全孔径数据进行PGA处理。
5 仿真分析
文献[9]中提及,因为机载 SAL系统束散角较小,在斜距为1.5 km时,成像幅宽仅有1 m左右,距离徙动对成像影响较小,可采用距离多普勒(Range Doppler, RD)算法进行成像。对振动条件下正侧视机载SAL进行成像仿真,仿真参数见表1。
5.1 振动影响仿真分析
在振动条件下检查回波信号全孔径时间与子孔径时间内的方位频谱,结果如图4与图5所示。在全孔径时间内,由于振动引起的相位误差变化较大,其带宽较宽,与原始发射信号方位频谱卷积后,使得接收信号的方位频谱明显展宽;反之,对于子孔径时间回波信号,由于在子孔径短时间内,振动引起的相位误差变化不大,接近线性相位,其与原始发射信号方位频谱卷积后,主要影响体现为频谱搬移。

表1 振动条件下正侧视机载SAL仿真参数Tab. 1 Simulation parameters of side-looking airborne SAL under vibration condition

图4 全孔径成像振动对信号方位频谱影响Fig. 4 Effect of vibration on signal azimuth frequency spectrum under full-aperture imaging condition
对5点十字目标场景(目标点距离向间距10 cm,方位向间距5 cm)分别进行全孔径与子孔径成像,成像结果见图6与图7。可以看到,全孔径成像时,目标在方位向散焦严重;而子孔径成像时,目标方位向轻微散焦,但几何位置发生明显错位,且不同子孔径位置偏离不同,无法直接进行多视处理。
5.2 单探测器仿真分析
使用文献[12]中的SPGA方法进行成像,全孔径成像结果和相位补偿后残余的相位误差分别见图8和图10。可以看到,残余相位误差接近1阶线性误差,这造成图8中目标点方位位置发生偏移。对目标中心点进行放大,中心点细节见图 9,发现在全孔径成像时,由于PGA估计的相位误差不够准确,无法达到理论分辨率(全孔径理论分辨率优于1 mm)。分别对原始回波数据与相位补偿后的数据进行多普勒域 26视处理,非相干叠加后的图像见图11和图12。经SPGA处理后的多视图像聚焦较好,能够达到方位向5 cm分辨率的系统设计要求(考虑到SPGA相位补偿不准确,将多视处理理论分辨率选为2.5 cm)。

图5 子孔径成像振动对信号方位频谱影响Fig. 5 Effect of vibration on signal azimuth frequency spectrum under sub-aperture imaging condition
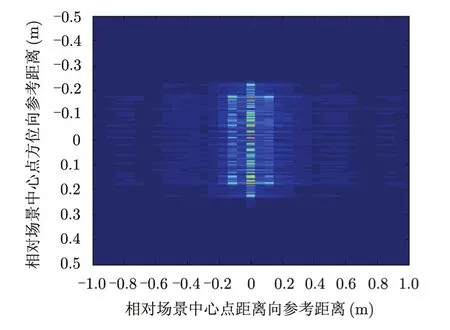
图6 全孔径RD成像结果Fig. 6 Full-aperture imaging result using RD algorithm

图7 单个子孔径RD成像结果Fig. 7 Sub-aperture imaging result using RD algorithm
采用图像拼接法进行成像处理,得到的多视非相干叠加图像见图14。作为比较,对各个慢时间子孔径不进行PGA处理和频谱搬移操作得到的多视结果见图13。可以看到,使用该方法得到的图像在方位向聚焦良好,且方位向位置准确。
为进一步验证单探测器情况下的两种成像方法的有效性,对全孔径方位分辨率约为0.1 m (距离分辨率0.5 m,方位向进行16视处理后分辨率约为1.6 m)的毫米波SAR数据添加振幅为20 mm,频率为1 Hz的等效振动相位误差,分别采用单探测器的两种方法进行成像处理。添加振动相位误差前后的多视成像结果分别见图15与图16,比较发现,添加振动相位误差后图像散焦严重,地物边缘十分模糊。使用两种方法进行多视成像,结果分别见图17与图18。使用两种方法得到的图像聚焦情况得到明显好转,且采用图像拼接方法得到的图像效果较好,接近添加振动相位误差前的图像,这验证了图像拼接法更适用于场景中缺少强点的情况。
5.3 顺轨双探测器仿真分析

图8 SPGA处理后全孔径成像结果Fig. 8 Full-aperture imaging result after SPGA processing

图9 对全孔径成像结果中心点放大Fig. 9 Detail of center point in full-aperture imaging result

图11 不进行SPGA处理的多视结果Fig. 11 Multilook result without SPGA processing

图12 SPGA处理后的多视结果Fig. 12 Multilook result after SPGA processing

图13 各子孔径不进行PGA处理多视结果Fig. 13 Multilook result without PGA for each sub-aperture

图14 各子孔径PGA处理后频谱搬移多视结果Fig. 14 Multilook result after PGA and frequency spectrum shifting for each sub-aperture

图16 添加振动相位误差的多视结果Fig. 16 Multilook result with vibration phase error

图17 SPGA处理后的多视结果Fig. 17 Multilook result after SPGA processing

图18 图像拼接法多视结果Fig. 18 Multilook result using image mosaic
下面对顺轨双探测器情况进行仿真,根据干涉测速结果估计振动相位误差,得到的结果见图19。可以看到,估计值与实际值十分接近,只是在数据边缘及相位误差大的地方有较大差异。补偿估计相位误差后,对全孔径进行PGA处理,得到的残余相位误差见图20,除数据边缘处,全方位向相位误差可控制在0.4 rad以内。采用干涉测速进行相位误差估计,减轻了全孔径进行PGA处理的压力,补偿相位误差后的数据可选择更小的窗口,这样提取的强点信息受到邻近目标的干扰更小,PGA估计的相位误差更为准确。下面选择同样的初始窗口进行全孔径PGA处理,图21与图23分别为直接进行全孔径PGA处理的全孔径成像结果与频域多视结果,图22与图24分别为补偿干涉估计的相位误差后进行全孔径PGA处理的全孔径成像结果与频域多视结果。比较发现,补偿干涉估计的相位误差后进行PGA处理,无论是全孔径成像还是频域多视处理都会得到聚焦良好的厘米级分辨率图像。

图19 由干涉相位估计的振动相位误差Fig. 19 Vibration phase error estimated by interferomatric phase

图20 相位补偿与PGA处理后的残余相位误差Fig. 20 Residual phase error after phase compensation and PGA processing

图21 仅使用PGA处理的全孔径成像Fig. 21 Full-aperture image only using PGA processing

图22 相位补偿与PGA处理后全孔径成像 Fig. 22 Full-aperture image after phase compensation and PGA processing

图23 仅使用PGA处理的多视结果Fig. 23 Multilook result only using PGA processing

图24 相位补偿与PGA处理后的多视结果 Fig. 24 Multilook result after phase compensation and PGA processing
6 结束语
本文分析了平台振动对机载 SAL成像的影响,研究了振动条件下单探测器与顺轨双探测器的成像处理方法,仿真结果验证了本文成像方法的有效性。
在振动条件下,本文首先考虑将机载SAL安装在稳定平台上,目前磁悬浮稳定平台有望将振动限制在更小的范围内,这将进一步减少振动对成像的影响,磁悬浮稳定平台的研究进展和应用很值得关注。与此同时,本文提出的顺轨双探测器成像方法在原理上也可解决大气湍流对 SAL成像的影响问题,相关的研究工作值得下一步深入开展。
[1] Liu Li-ren. Coherent and incoherent synthetic-aperture imaging ladars and laboratory-space experimental demonstrations[J]. Applied Optics, 2013, 52(4): 579-599.
[2]吴谨. 关于合成孔径激光雷达成像研究[J]. 雷达学报, 2012, 1(4): 353-360.
Wu Jin. On the development of synthetic aperture ladar imaging[J]. Journal of Radars, 2012, 1(4): 353-360.
[3]郭亮, 邢孟道, 张龙, 等. 室内距离向合成孔径激光雷达成像的实验研究[J]. 中国科学 E辑: 技术科学, 2009, 39(10): 1678-1684.
Guo Liang, Xing Meng-dao, Zhang Long, et al.. Research on indoor experimentation of range SAL imaging system[J]. Science China Technological Sciences, 2009, 39(10): 1678-1684.
[4] Krause B W, Buck J, Ryan C, et al.. Synthetic aperture ladar flight demonstration[C]. Optical Society of America/ Conference on Lasers and Electro-optics (OSA/CLEO), Maryland, USA, 2011: PDPB7.
[5]李增局, 吴谨, 刘国国, 等. 振动影响机载合成孔径激光雷达成像初步研究[J]. 光学学报, 2010, 30(4): 994-1001.
Li Zeng-ju, Wu Jin, Liu Guo-guo, et al.. Preliminary investigation on airborne SAL imaging with platform vibration[J]. Acta Optica Sinica, 2010, 30(4): 994-1001.
[6]洪光烈, 郭亮. 线振动对合成孔径激光雷达成像的影响分析[J].光学学报, 2012, 32(4): 0428001-1-0428001-7.
Hong Guang-lie and Guo Liang. Analysis of effects of line vibration on imaging quality of synthetic aperture ladar[J]. Acta Optica Sinica, 2012, 32(4): 0428001-1-0428001-7.
[7]徐显文, 洪光烈, 凌元, 等. 合成孔径激光雷达振动相位误差的模拟探测[J]. 光学学报, 2011, 31(5): 0512001-1-0512001-7.
Xu Xian-wen, Hong Guang-lie, Ling Yuan, et al.. Simulative detection of vibration phase error of synthetic aperture lidar[J]. Acta Optica Sinica, 2011, 31(5): 0512001-1-0512001-7.
[8]吕旭光, 郝士琦, 冷蛟锋, 等. 基于自适应窗的合成孔径激光雷达联合时频成像方法[J]. 光子学报, 2012, 41(5): 575-580.
Lv Xu-guang, Hao Shi-qi, Leng Jiao-feng, et al.. Combined time-frequency imaging method of SAL based on adaptive windowing[J]. Acta Photonica Sinica, 2012, 41(5): 575-580.
[9]李道京, 张清娟, 刘波, 等. 机载合成孔径激光雷达关键技术和实现方案分析[J]. 雷达学报, 2013, 2(2): 143-151.
Li Dao-jing, Zhang Qing-juan, Liu Bo, et al.. Key technology and implementation scheme analysis of air-borne synthetic aperture ladar[J]. Journal of Radars, 2013, 2(2): 143-151.
[10]保铮,邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 196-200.
Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 196-200.
[11]Eichel P H, Ghiglia D C, and Jakowatz Jr C V. Speckle processing method for synthetic-aperture-radar phase correction[J]. Optics Letters, 1989, 14(1): 1-3.
[12]孟大地, 丁赤飚. 一种用于条带式 SAR的自聚焦算法[J]. 电子与信息学报, 2005, 27(9): 1349-1352.
Meng Da-di and Ding Chi-biao. A new approach to autofocus considering strip map SAR[J]. Journal of Electronics & Information Technology, 2005, 27(9): 1349-1352.
[13]Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Norwood, MA, USA, Artech House, Inc., 2005: 369-421.
[14]Chan H L and Yeo T S. Noniterative Quality Phase-Gradient Autofocus (QPGA) algorithm for spotlight SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1531-1539.
[15]尹建凤, 李道京, 吴一戎. 顺轨三频三孔径星载 SAR的运动目标检测及定位方法研究[J]. 电子与信息学报, 2010, 32(4): 902-907.
Yin Jian-feng, Li Dao-jing, and Wu Yi-rong. Research on the method of moving target detection and location with three-frequency three-aperture along-track spaceborne SAR[J]. Journal of Electronics & Information Technology, 2010, 32(4): 902-907.
[16]李道京, 汤立波, 吴一戎, 等. 顺轨双天线机载 InSAR的地面运动目标检测研究[J]. 电子与信息学报, 2006, 28(6): 961-964.
Li Dao-jing, Tang Li-bo, Wu Yi-rong, et al.. Ground moving target indication based on along track airborne InSAR with two antennas[J]. Journal of Electronics & Information Technology, 2006, 28(6): 961-964.
[17]Crouch S C and Barber Z W. Laboratory demonstrations of interferometric and spotlight synthetic aperture ladar techniques[J]. Optics Express, 2012, 20(22): 24237-24246.
[18]Crouch S C. Synthetic aperture ladar techniques[D]. [Master dissertation], Montana State University, 2012: 59-77.

马 萌(1989-),男,河南周口人,中国科学院电子学研究所在读硕博连读生,研究方向为雷达信号处理。
E-mail: mameng_ee@163.com

李道京(1964-),男,陕西西安人,中国科学院电子学研究所研究员,博士生导师,主要研究方向为雷达系统和雷达信号处理。
E-mail: lidj@mail.ie.ac.cn

杜剑波(1991-),男,安徽滁州人,中国科学院电子学研究所在读硕博连读生,研究方向为雷达信号处理。
E-mail: jianbodu1991@163.com
Imaging of Airborne Synthetic Aperture Ladar under Platform Vibration Condition
Ma Meng①②③Li Dao-jing①②Du Jian-bo①②③①(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)②(Science and Technology on Microwave Imaging Laboratory, Beijing 100190, China)
③(University of Chinese Academy of Sciences, Beijing 100049, China)
This study examines the imaging problems in airborne synthetic aperture ladar with single detector and dual detectors along tracks under platform vibration condition. Because platform vibrations affect imaging processing for short intervals negligibly, a method uniting the subaperture imaging and phase gradient autofocus is considered for single-detector ladar. To obtain long stripmap images in azimuth, the stripmap phase gradient autofocus method and the subaperture image mosaic process using Doppler centroid estimation are used. Their performance is analyzed and compared. Considering the shortage of single-detector ladar, a method based on along-track dual-detector interferometric processing is proposed to estimate and compensate for the vibration phase error. The simulation verifies the effectiveness of the proposed methods.
Ladar; Synthetic aperture; Imaging processing; Platform vibration
TN958.98
A
2095-283X(2014)05-0591-12
10.3724/SP.J.1300.2014.13132
2013-12-18 收到,2014-03-12改回;2014-10-14网络优先出版国家自然科学基金(61271422)资助课题
*通信作者: 马萌 mameng_ee@163.com

