基于PCNN和非线性滤波万有引力的医学图像融合

刘雯敏，陈秀宏

江南大学 数字媒体学院，江苏 无锡 214122

基于PCNN和非线性滤波万有引力的医学图像融合

刘雯敏，陈秀宏

江南大学 数字媒体学院，江苏 无锡 214122

1 引言

图像融合技术[1]是通过多个成像方式不同的传感器采集到关于同一个具体目标或场景的图像信息，然后按照一定的规则加以综合处理，生成一个新的信息量更大、对周围环境适应性更高的解释。这个解释是从单一传感器获取的信息中无法得到的，是对目标或场景的描述更加准确、可靠和全面的图像。目前，图像融合技术在计算机视觉、遥感技术、军事应用以及医学图像处理等领域都表现出巨大的应用潜力。特别是当今医学成像已经成为现代医疗诊断不可或缺的一部分，迫切需要高质量的医学图像融合方法将有效的信息进行融合。

近年来国内外常见的医学图像融合方法有加权平均、局域方差、基于多分辨率塔式融合算法和神经网络方法[2-4]等。其中，基于小波变换的多分辨率融合算法应用最为广泛，但该方法存在丢失某些微弱细节信息等不足，在处理大量的医学图像数据时计算复杂、实时性差。针对这一问题，本文采用提升小波变换对医学图像进行处理。提升小波变换能够降低运算的复杂程度、减少存储器开销和提高运算速度，从而降低了医学图像融合过程的难度。为了使融合图像反映出更加真实完整的信息，本文将提升小波变换和符合生物视觉特性的脉冲耦合神经网络[5]（Pulse Coupled Neural Networks，PCNN）相结合，并将图像像素非线性滤波的万有引力定义为PCNN的链接强度，使得链接强度的大小能够根据图像自适应调整，保留更多的细节信息。实验结果表明，该方法能够更加有效地保留源图像中的边缘及细节信息，提高了医学图像的融合质量。

2 理论基础

2.1 提升小波变换

传统的小波变换是在欧氏空间内通过基底的平移和伸缩构造小波基的，不适合于非欧氏空间的应用，因此小波提升方案应运而生。1995年Sweldens等人提出了一种区别于小波变换，不依赖于傅里叶变换的新的小波构造方法——提升格式[6]（Lifting Scheme），称之为第二代小波变换，它在保持第一代小波特性的基础上克服了其平移和伸缩的不变性，同时提供了一种快速的实现方式，使小波变换的运算复杂度降低一半，提高了运算速度。提升的实现形式给出了小波完全的空间域解释，可以在原有小波的基础上构造出更有效地适用于特殊应用的小波。它从另一个角度给小波的构造和性质作出了解答。同时它也把数值分析领域的“细分插值”、“均值插值”、“高阶矩”、“欧拉算法”等概念和小波分析的“消失矩”、“尺度函数”、“小波函数”等概念巧妙地融合为一体。

提升算法给出了双正交小波简单而有效的构造方法，使用了基本的多项式插补来获取信号的高频分量，然后通过“保持原信号的均值和高阶矩不变”的限制条件来获取信号的低频分量。提升算法的基本思想是，将现有的小波滤波器分解成基本的构造模块，分步骤完成小波变换。

提升方案把第一代小波变换过程分为以下三个步骤[6-7]：分裂（Split）、预测（Predict）和更新（Update）。

（1）分裂：将原始数集S(j)={s(kj),k∈Z}（j=0，1，…，N为分裂层次）分为两个较小子集，最简单的分裂方法就是输入信号根据奇偶性分为两组。分别为偶数样本集 S(j0)={,k∈Z}和奇数样本集 S(j1)={,k∈Z}，即 split(S(j))=(S(j0)，S(j1))。这个过程称为懒小波（Lazy Wavelet）变换。

（2）预测：在这个阶段，保持偶数样本S(j0)不变，在基于原始数据相关性的基础上，利用偶数样本S(j0)来对奇数样本S(j1)做出预测，即将滤波器P对偶数样本作用后作为奇样本的预测值，用奇样本的实际值与预测值P(S(j0))相减得到残差信号（又可称为细节系数）来代替奇数样本S(j1)，即令S(j1)=S(j1)-P(S(j0))，其中 P为预测算子。这一差值反映了两者之间的逼近程度，称之为细节系数或者小波系数，对应于原始信号S(j)的高频部分。一般来说，数据的相关性越强，小波系数的幅值就越小，预测就越准确。

（3）更新：经过分裂步骤后产生子集的某些特征可能与原始数据并不一致，更新操作的思想就是要找到一个更好的子数据集S(j-1)，使它能够保持原始数据集S(j)的某些特性。可以利用已经计算好的小波系数S(j1)，构造算子U，作用在S(j1)上并叠加到偶数样本S(j0)上，从而得到更新后的近似信号，即：S(j0)=S(j0)+U(S(j1))。

P和U取不同的函数，可构造出不同的小波变换。

经过小波提升，可将样本 S(j)分解为低频部分S(j0)和高频部分S(j1)；对于低频数据子集S(j0)可以再进行相同的分裂、预测和更新，把S(j0)进一步分解为S(j-1，0)和S(j-1，1)；…；如此下去，经过n次分解后，原始数据S(j)的提升小波表示为{S(j-n，0)，S(j-n，1)，S(j-n+1，1)，…，S(j-1，1)}。其中S(j-n，0)表示信号的低频部分，而{S(j-n,1),S(j-n+1,1),…, S(j-1，1)}则是信号从低到高的高频部分系列[7-9]。

由于图像的小波提升是一个完全可逆的过程，反变换与正变换运算相反并且结构对称，可以实现精确的重构。重构过程是分解过程的逆步骤，三个步骤分别为：

（1）反更新：S(j0)=S(j0)-U(S(j1))。

（2）反预测：S(j1)=S(j1)+P(S(j0))。

（3）合并：把偶数样本S(j0)和奇数样本S(j1)合并成新的数据集S(j)，即S(j)=merge(S(j0)，S(j1))。

提升算法的分解和重构过程如图1所示。

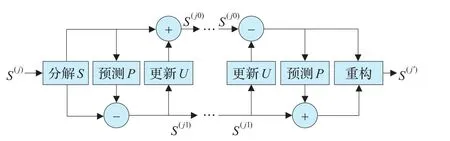
图1 提升算法的分解和重构过程

2.2 脉冲耦合神经网络（PCNN）

脉冲耦合神经网络是由若干个神经元相互链接所构成的反馈型神经网络，每个神经元由三个功能单元构成：反馈输入域、耦合链接输入域和脉冲发生器。Eckhorn神经元模型[5]参数较多，在具体应用中参数的设定十分麻烦。也缺乏诱异激发所指的同步振荡的明确描述，就是说在图像分析时，缺乏灰度值相近的相邻（像素对应）神经元产生同步振荡脉冲输出所构成的相似像素集群概念的清晰数学描述，导致类似研究成果的分析比较困难。为此，众多文献对Eckhorn神经元模型做了种种改进，得到许多改进的神经元模型[10-12]。文献[12]中修正后的模型简洁直观，如图2所示。因此，本文在进行医学图像融合时就采用这个简化的PCNN模型。

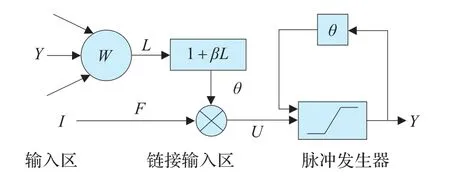
图2 脉冲耦合神经元的简化模型

PCNN模型在用于图像处理时是一个单层二维并且横向连接的神经网络，网络中的神经元是与图像中的像素点一一对应的，即图像中任意像素点(i，j)对应在PCNN中神经元的位置也为(i，j)。神经元Nij经过n次迭代的数学表达式如下：

其中，i，j表示像素在图像矩阵中的位置；Iij为外部刺激输入，图像处理时为对应点像素的灰度值；n为迭代次数；Uij、Yij分别为神经元的内部状态信号和外部输出；Lij、Fij分别为链接输入和反馈输入；β为链接强度；Wijkl为链接权值矩阵；αL、αθ和θij分别为衰减时间常数和动态门限；VL、Vθ分别为链接输入和动态门限的放大系数。

在上述模型中，首先接收域接收到外部的输入刺激Iij；在接受输入后调制部分就利用周围神经元的耦合链接Lij和链接强度 β，来确定神经元耦合关系的强弱并对接收部分的信号进行调制，来确定神经元耦合关系的强弱并对接收部分的信号进行调制，则产生神经元内部活动信号Uij；之后Uij与此时脉冲发生器产生的动态阈值θij做比较，便可产生此刻的输出信号Yij。如果Uij＞θij，则Yij=1，称为神经元点火，点火成功则输出一个脉冲；如果Uij≤θij，则Yij=0，没有点火则不输出脉冲。若神经元点火成功有脉冲输出，则其动态阈值就会突然增加，又因为阈值突然增大使第二次不可能再次点火成功而产生脉冲输出，于是之后阈值又开始呈指数衰减，直到阈值衰减到小于其内部活动项时，脉冲又再次产生，如此不断地周而复始直至达到迭代次数n。

式（1）中描述的PCNN模型有很多参数，这些参数的设定对图像处理的结果也有很大的影响，但在理论上其参数的设定与图像处理结果之间的机理还不十分清楚。因此参数设定一直是PCNN应用的一个难题。大多数情况下，这些参数的设定都是根据具体的应用环境通过多次实验的方法确定的，近年也出现了一些PCNN参数自动设定方法的相关研究[13-14]。

（1）VL和Vθ分别为PCNN链接输入和动态门限的放大系数，VL对周围神经元的耦合输入进行比例限制，通常取值为1。Vθ对神经元的点火周期起着重要的调节作用，它决定了神经元点火时刻阈值将被提升的程度。通常Vθ取值较大[8]，本文中取Vθ=25。

（2）αL和αθ分别为链接输入和动态门限的衰减时间常数，αθ控制着动态门限下降的速度，αθ越大，动态门限下降越慢，PCNN模型运行时间越长；反之，动态门限下降越快，模型运行时间越短。通常这两个参数都是根据经验值再结合具体应用多次实验设定的，本文中通过多次实验取αL=0.2，αθ=0.2。

（3）Wijkl为链接权值矩阵，表示了中心神经元受周围神经元影响的大小，反映邻近神经元对中心神经元传递信息的强弱。Wijkl有多种取值方式，本文中用到的取值方式为欧几里德距离的倒数，在3×3的区域则有W=

（4）β为链接强度系数，调节着周围神经元之间的相互影响，同时影响中心神经元点火周期，较大的链接系数能引起较大范围的脉冲同步。链接强度系数通常都是根据经验和多次实验手工设定的固定值，大多数情况下 β是一个在[0，1]区间上的常数。本文中为了提高医学图像融合的质量，并增强PCNN的自适应能力，链接强度系数β并不设定为一个常数，而设置为一个动态变化的参数。

2.3 基于非线性滤波的万有引力

万有引力定律是经典物理学中的一个定义，它描述了宇宙中任何两个物体间都存在着相互吸引力，有其中任一物体所受到的引力大小与两个物体质量的乘积成正比，与两物体之间距离的平方成反比，可用式（2）表示：

其中，m1，m2分别为两物体的质量，G为万有引力常量，||r||为两物体之间的距离。

Sun等人[15]将这一经典的物理概念运用到图像处理中，将图像中的每个像素点都看作为宇宙中的一个物体，并认为每两个像素点之间都存在引力，这样一幅图像就可以被理解为一个由许多物体组成的网格结构。为了方便处理，在简化模型中规定引力的作用范围是中心像素点3×3或5×5的邻域内，在邻域外的点对中心像素点的万有引力则忽略不计。其中，每一对水平或竖直方向邻接的像素间的距离为1，像素的质量取其对应的灰度值。如式（2）中所示，引力用向量表示，即两个像素点之间的万有引力为 f，窗口内所有其他像素点对中心像素点的引力合力为F。对图像的每一个像素点，首先计算它的领域内其他像素点对它的引力 f，然后合并所有的 f，得到这个像素点在领域内所受的水平方向和垂直方向的合力Fx和Fy，最后得到总合力的大小为||F||=。文献[15]将这个合力运用到边缘检测中，通过设置一个阈值，合力大于阈值的即为边缘点，否则为非边缘点。这个方法大胆新颖，并在边缘检测上取得了很好的效果。但是检测到的边缘较宽，并且严重依赖图像的灰度值。

文献[16]就在此基础上进行了改进，提出了基于非线性滤波的万有引力边缘检测方法。对图像中任一像素点(i，j)，其灰度值为 I(i，j)，则基于非线性滤波的万有引力方法如下：

（1）计算其水平方向质量为：

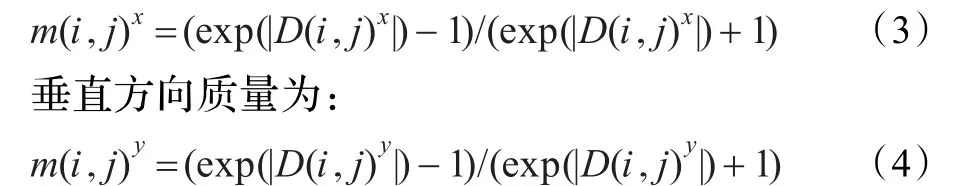
其中，引入了一个非线性梯度的概念，D(i，j)x=+ D(i，j)-x为像素点的水平梯度，而 D(i，j)+x=T(I(i，j)-I(i-1，j))和 D(i，j)-x=-T(-(I(i+1，j)-I(i，j)))分别为水平梯度的左右梯度信息；D(i，j)y=D(i，j)+y+D(i，j)-y为垂 直 梯度，D(i，j)+y=T(I(i，j)-I(i，j-1))和 D(i，j)-y= -T(-(I(i，j+1)-I(i，j)))分别为垂直梯度的左右梯度信息；非线性算子T是一个简单的阈值，如果X≥0，T(X)= X；否则T(X)=0。

这个梯度不仅定位准确，而且有一定的平滑噪声的能力，所以构造以这个梯度为自变量的函数，替代中心像素点的灰度值，作为万有引力中心物体的质量。这个函数需要满足下列特性：当像素点梯度为零时，函数值为零；函数值随梯度值增加而增加；当梯度值趋向无限大时，函数值趋近于1。所以构造出了求质量的式（3）和（4）。

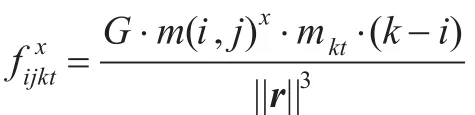
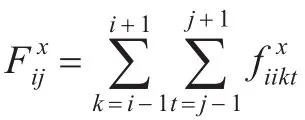
（4）计算中心像素点I(i，j)所受总合力大小及方向。大小为||Fij||=；方向为θ=arctan()。

在文献中使用到非线性滤波的万有引力来与阈值比较，从而判断图像中的某一点是否为边缘点，该方法具有很好的图像边缘定位能力[16]，能够高质量地反映出图像中微小细节的反差和边缘化的程度。鉴于这个优点，于是本文中就引入这一概念和方法，通过该方法求出图像中每个像素的非线性滤波万有引力，并构成矩阵B。将矩阵B归一化后作为链接强度系数输入到耦合神经网络中，作为中心神经元调节与周围神经元之间关系的一个依据。

3 基于PCNN和非线性滤波万有引力的图像融合方法

在提升小波变换的基础上，并且结合耦合神经网络和像素点非线性滤波的万有引力，本文中的医学图像融合过程如下：

（1）将已精确配准的CT和MRI图像分别进行N层提升小波分解，得到1个低频分量和3N个高频分量，则原图像CT和MRI经过N层提升小波分解得到的低频分量为 LCT和 LMRI，高频分量为和(k=1，2，…，3N)。

（2）低频系数的融合规则。由于低频分量(L)代表图像的近似特征和缓变的区域信息，特别是在医学图像中能够对病灶的定位起到重要的作用。因此采用区域灰度均值作为判断的标准。窗口宽度为n×n的局部灰度均值定义为：

其中I(i，j)为像素点(i，j)的灰度值，w是窗口范围。从而得低频部分融合后图像像素点灰度值LF(i，j)为：

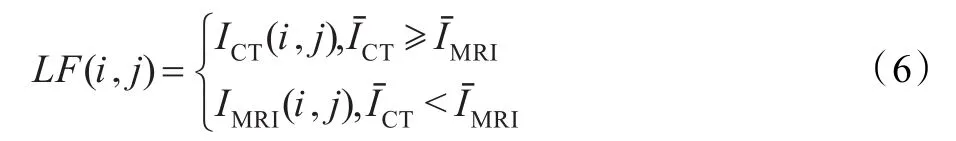
（3）高频系数的融合规则。高频分量(H)代表的是图像边缘等突变的细节信息，对最后融合图像的边缘细节信息有决定性的作用，因此将PCNN和利于保留像素边缘的非线性滤波万有引力方法相结合作为高频分量的融合规则。

简化PCNN模型的关键点就在于链接强度β上，以往使用PCNN进行图像处理时，都是根据经验或大量实验设定β为一个固定的数值，这样的方法就缺少自适应性，无法获得微小的细节信息。由人眼的视觉系统对图像的边缘信息以及微小的细节信息较为敏感的特性可知，脉冲耦合神经网络中神经元的链接强度也应该是与图像的边缘细节信息有关的。因此，本文考虑到利用像素点的非线性滤波万有引力来对链接系数进行动态调整，即有 β=B，使网络中的神经元有不同的链接强度。像素点的非线性滤波万有引力较大，对应神经元的链接强度就较大，该像素点对应的神经元被捕获点火就越早。就可以根据图像领域大小内其他像素点对中心像素的非线性滤波万有引力的变化来自适应调整PCNN的链接强度，使融合结果更加符合人类视觉的特点，就更有利于提高图像的融合效果。

③设置PCNN中各参数的初始值，如放大系数、衰减时间常数和链接权值矩阵等。

④采用式（1）计算各个中间结果，完成N次迭代的过程。最后输出两个点火矩阵和。

⑤最后由下式得到高频子系数的融合结果HF，

（4）对融合后的子系数LF和HFk(k=1，2，…，3N)进行提升小波逆变换，得到最终的融合图像F。

上述融合过程如图3所示。

图3 融合算法流程图

4 评价指标

医学图像的融合目的一方面是提高信息量，并保留图像的边缘等细节信息以加强图像的视觉效果。另一方面，医学图像融合的结果需要与原图像保持最大的一致，同时保持与两幅待融合图像最大的相关性。基于以上原因在图像融合现有的评价指标中选取下列指标对融合效果进行评价[17]。

4.1 信息熵

图像的信息熵的含义为图像的平均信息量，而信息量的增加是图像融合的最基本要求。因此信息熵是衡量融合图像信息丰富程度的一个重要指标，体现了融合图像的细节表达能力。融合图像的熵值越大，就表明图像携带的信息量越大，包含的信息越丰富，图像的表达能力越好。信息熵定义为：

其中，L为图像的总灰度级数，Pi为图像中灰度级数为i的像素出现的概率。

4.2 均值

均值是图像中所有像素的灰度的平均值，反映了融合图像的平均亮度。最后得到的融合图像的均值适中则该融合图像的视觉效果好。

其中，图像大小为m×n，I(i，j)为像素点(i，j)的灰度值。

4.3 平均梯度

融合图像质量的改进可以用平均梯度来表示，因为图像的平均梯度反映的是图像的清晰度，同时还反映出图像中微小细节反差和纹理变换特征。融合图像的平均梯度越大，就表示图像的成像越清晰。图像的平均梯度定义为：

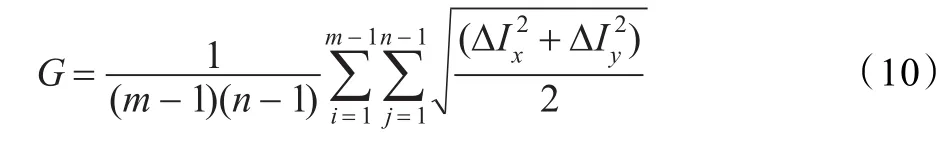
其中，图像大小为 m×n，ΔIx=I(i，j)-I(i+1，j)，ΔIy= I(i，j)-I(i，j+1)分别为像素值(i，j)在x/y方向上的一阶差分。

4.4 空间频率

图像的空间频率[18]是反映图像空间域的总体活跃度。融合图像的空间频率越大，则其总体活跃度越高，融合图像的效果就越好。

4.5 边缘保持度

图像的边缘保持度可以衡量融合图像对输入的源图像中的边缘信息的保持程度[19]。该方法在对源图像和融合图像进行边缘提取的基础上，计算边缘信息的保持量，将加权的边缘信息保存量作为评价融合结果的衡量指标，边缘保持度越大，说明融合图像保留的源图像的边缘信息越多。边缘保持度的具体求解步骤如下：

（1）计算源图像IA、IB以及融合图像IF的梯度幅值和相角，以计算IA的为例：

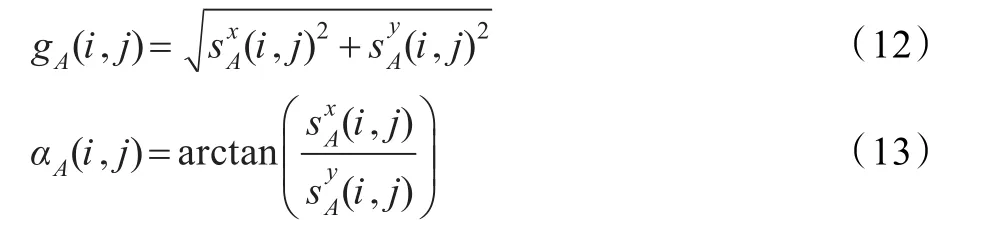
式中，sAx(i，j)和 sAy(i，j)分别为应用Sobel算子对图像IA进行横向和纵向滤波的结果。

（2）计算 IA与 IF、IB与 IF的相对幅值GAF(i，j)、GBF(i，j)和相角 AAF(i，j)、ABF(i，j)。以计算GAF(i，j)和AAF(i，j)为例。

（4）计算各像素边缘信息的保留程度：

式中，图像大小为 m×n，wA(i，j)=|gA(i，j)|L，wB(i，j)= |gB(i，j)|L。L为常数，本文中取1。

5 实验与结果分析

实验采用两组CT和MRI医学图像进行融合，两组源图像来自人体脑部的不同横断面。数据的源图像都来自同一个人、同一生理部位的不同成像设备，空间位置和解剖结构都是精确对准的。源图像如图4所示。

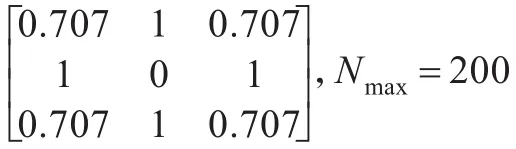
为了更加客观定量评价融合效果，本文采用信息熵、平均梯度、边缘保持度、均值和空间频率作为融合结果的评价参数。其中信息熵反映了图像信息的丰富程度；平均梯度反映了图像的清晰度；边缘保持度用于衡量融合图像对输入图像中的边缘信息的保持程度；均值反映了图像的平均亮度；空间频率则反映了图像空间域的总体活跃度。这些参数均是越大，融合图像的效果越好。比较结果如表1和表2所示。

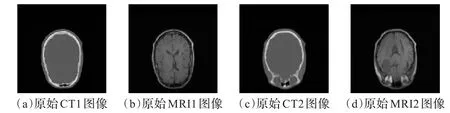
图4 两组源图像

图5 CT1与MRI1各方法融合结果比较

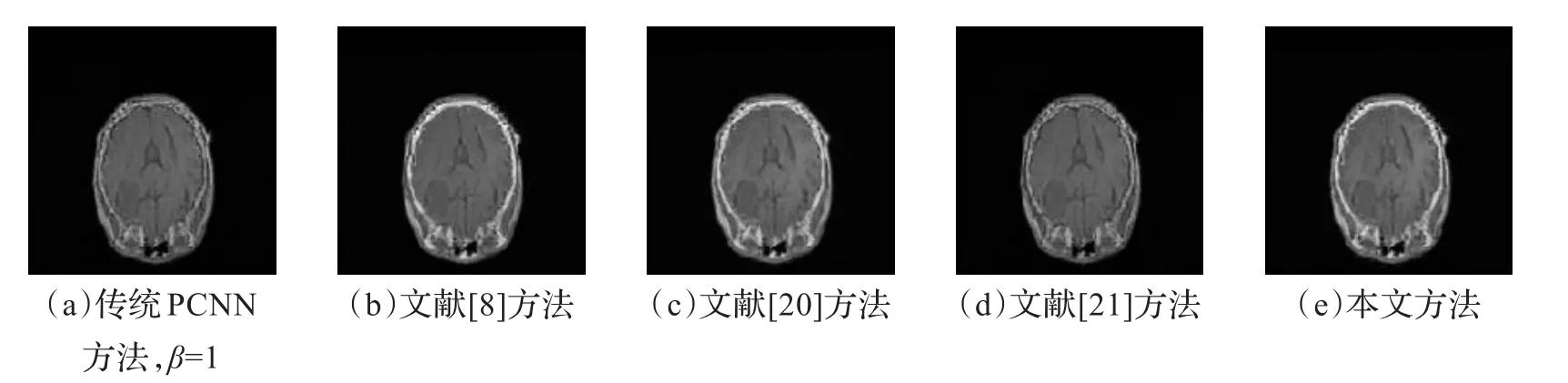
图6 CT2与MRI2各方法融合结果比较

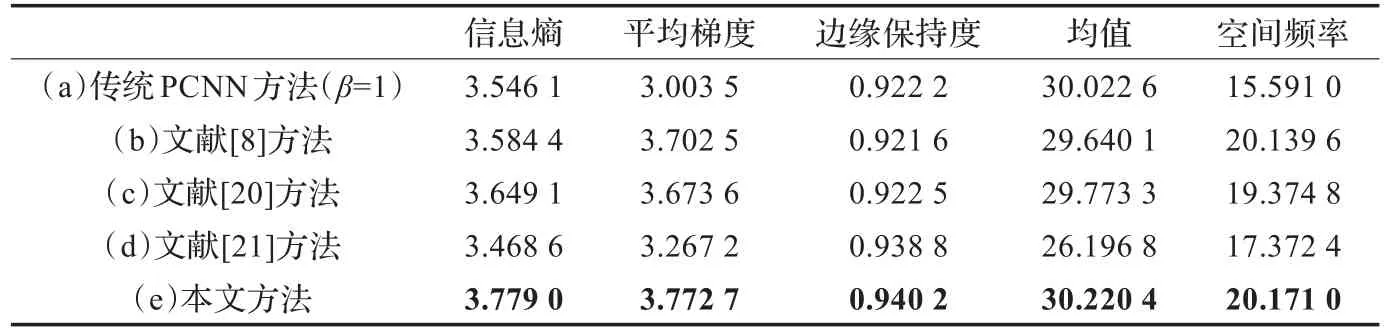
表1 图5中各个融合结果的评价参数

表2 图6中各个融合结果的评价参数

图7 CT1与MRI1各方法融合结果边缘提取图

图8 CT2与MRI2各方法融合结果边缘提取图

由表1和表2可知，这些融合方法都取得了不错的融合效果，其中，传统的融合方法参数相较之下均值较大，即有较好的视觉效果；文献[8]的方法空间频率较高；文献[20]的方法信息熵较高，包含的信息较丰富；文献[21]的方法则是有较高的边缘保持度。本文方法融合图像的信息熵最大，即包含了更多细节信息；平均梯度相比也有所提高，即增加了融合图像的清晰度；均值即平均亮度的提高改善了视觉效果；空间域的总体活跃度也较高。所以本文中的融合方法得到的融合图像质量最好。

为了更直观地表现融合算法的效果，对上述实验结果再采用Canny算子进行边缘提取，提取结果如图7和图8所示。可以发现，本文方法的边缘细节信息得到了更好的保留，边缘更加连续。因此，本文方法在进行医学图像诊断时能够提供更多的细节信息，满足医学图像日益多样化和复杂化的需要。

6 结束语

图像中目标的边缘和轮廓是其重要的特征，特别是在医学图像中，不同的边缘代表的是不同组织或器官的界限。本文在提升小波变换的基础上，将脉冲耦合神经网络和边缘提取性能很好的非线性滤波万有引力方法相结合，构成具有自适应能力的PCNN，并将其应用到反映图像边缘细节信息的高频子图像的融合规则中，这样可有效地保留源图像的不同信息，强化了边缘和纹理特征。实验结果表明，本文的图像融合方法改善了融合图像的视觉效果，提高了各个评价参数质量，为医学诊断和治疗提供了更有效、更细节、更清晰的信息，在多模态医学图像融合处理中具有有效性和先进性以及广阔的应用前景。

[1]Mallat S G.A theory for multiresolution signal decomposition：the wavelet representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11（7）：674-693.

[2]张强，周海银，王炯琦.基于局部方差和高通滤波的小波变换图像融合[J].计算机仿真，2008，25（8）：223-226.

[3]Wen C Y，Chen L K.Multi-resolution image fusion technique and its application to forensic science[J].Forensic Science International，2004，140：217-232.

[4]Li Wei，Zhu Xuefeng.A new algorithm of multi-modality medical image fusion based on pulse-coupled neural networks[C]//Lecture Notes in Computer Science，2005，3610：995-1001.

[5]Eckhorn R，Reitboeck H J，Arndt M，et al.Feature linking via synchronization among distributed assemblies：simulation of results from cat cortex[J].Neural Computation，1990，2（3）：293-307.

[6]Daubechies I，Sweldens W.Factoring wavelet transforms into lifting steps[J].Journal of Fourier Analysis and Application，1998，4（3）：247-269.

[7]Peng Lizhong，Chu Xiaoyong.The lifting scheme of 4-channel orthogonal wavelet transforms[J].Progress in Natural Science，2006，16（1）：100-104.

[8]杨艳春，党建武，王阳萍.基于提升小波变换与自适应PCNN的医学图像融合方法[J].计算机辅助设计与图形学学报，2012，24（4）：494-499.

[9]Ranganath H S，Kuntimad G，Johnson J L.Pulse coupled neural networks for image processing[C]//Southeastcon’95，Raleigh，NC，1995：37-43.

[10]Kuntimad G，Ranganath H S.Perfect image segmentation using pulse coupled neural networks[J].IEEE Transactions on Neural Networks，1999，10（3）：591-598.

[11]Johnson J L，Padgett M L.PCNN models and applications[J].IEEE Transactions on Neural Networks，1999，10（3）：480-498.

[12]Ranganath H S，Kuntimad G.Iterative segmentation using pulse coupled neural networks[C]//Proceedings SPIE，1996，2760：543-554.

[13]Ma Yide，Dai Rolan，Li Lian，et al.Image segmentation of embryonic plant cell using pulse-coupled neural networks[J].Chinese Science Bulletin，2002，47（2）：167-172.

[14]马义德，齐春亮.基于遗传算法的脉冲耦合神经网络自动系统的研究[J].系统仿真学报，2006，18（3）：722-724.

[15]Sun G Y，Liu Q H，Liu Q，et al.A novel approach for edge detection based on the theory of universal gravity[J]. Pattern Recognition，2007，40（10）：2766-2775.

[16]张春雪，陈秀宏.基于非线性滤波的万有引力边缘检测方法[J].计算机应用，2011，31（3）：763-766.

[17]Qu Guihong，Zhang Dali，Yan Pingfan.Information measure for performance of image fusion[J].Electronic Letters，2002，38（7）：548-551.

[18]陈美玲，陶玲，钱志余.一种改进的医学图像融合技术及其效果[J].生物医学工程学杂志，2009，26（4）：711-715.

[19]Xydeas C S，Petrovic V.Objective image fusion performance measure[J].Electronic Letters，2000，36（4）：308-309.

[20]薛寺中，周爱平，梁久祯.基于小波变换的自适应脉冲耦合神经网络图像融合[J].计算机应用，2010，30（12）：3225-3228. [21]邹北骥，胡艺龄，辛国江.基于小波分解和PCNN的图像融合方法[J].计算机工程与科学，2011，33（2）：102-106.

LIU Wenmin,CHEN Xiuhong

School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China

In order to better meet the modern medicine clinical diagnosis and treatment needs,improve the medical image fusion quality,this paper proposes a new medical image fusion algorithm based on lifting wavelet transform,combined with the Pulse Coupled Neural Networks（PCNN）and pixel point of nonlinear filtering gravitation.A fusion rule based on the area average gray is adopted in low-frequency coefficients.Adaptive PCNN fusion rule is adopted in high-frequency coefficients.It makes the pixel’s nonlinear filtering gravitation as the linking strength of simplified PCNN model.So PCNN can adaptively control the size of linking strength,and according to the ignition matrix to determine the fusion of high-frequency coefficients.Experiments show that the fused image obtains more edge detail information than other methods and every index has improved.It has a better fusion performance.

medical image fusion;lifting wavelet transform;Pulse Coupled Neural Networks（PCNN）;nonlinear filtering gravitation;linking strength

为了更好地满足现代医学临床诊断和治疗的需要，提高医学图像的融合质量，提出在提升小波变换的基础上，结合脉冲耦合神经网络（PCNN）和像素点的非线性滤波万有引力的医学图像融合方法。低频子系数采用基于区域灰度均值的融合规则；高频子系数采用自适应PCNN的融合规则，将像素的非线性滤波万有引力作为简化的PCNN模型中的链接强度，使PCNN能够自适应调节链接强度的大小，并根据点火矩阵确定高频子系数。实验结果表明，该方法得到的融合图像比其他融合方法保留了更多的边缘细节信息，各项评价指标均有所提高，有更好的融合性能。

医学图像融合；提升小波变换；脉冲耦合神经网络；非线性滤波万有引力；链接强度

A

TP391.4

10.3778/j.issn.1002-8331.1301-0250

LIU Wenmin,CHEN Xiuhong.Medical image fusion method based on PCNN and nonlinear filtering of gravitation. Computer Engineering and Applications,2014,50（24）：191-198.

中央高校基本科研业务费专项资金资助（No.JUSRP211A70）。

刘雯敏（1989—），女，硕士研究生，主要研究方向：计算机图形与图像处理；陈秀宏（1964—），男，博士，教授。

2013-01-22

2013-04-02

1002-8331（2014）24-0191-08

CNKI网络优先出版：2013-04-18，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130418.1618.015.html