基于量子信息拆分的多人验证签名方案

张 琼，谭晓青

暨南大学 信息科学技术学院 数学系，广州 510632

基于量子信息拆分的多人验证签名方案

张 琼，谭晓青

暨南大学 信息科学技术学院 数学系，广州 510632

1 引言

数字签名作为密码学的重要分支是实现网络身份认证、数据完整性保护和非否认性服务的基础，也是开展电子商务和签订电子合同的重要工具。经典密码学的数字签名方案由于是基于计算上安全的，它们的安全性受到像量子计算机等高运算能力计算机的严重威胁，届时几乎所有的方案将会被轻易地攻破。自2001年Gottesman和Chuang[1]利用量子单向函数和量子交换实验提出第一个对数字消息的量子签名方案以来，之后研究者把签名的消息从经典消息扩展到任意的已知和未知的量子消息，并基于量子特性设计了很多新颖的量子签名方案[2-22]，主要可以分为仲裁量子签名[2-8]、量子多重签名[9-11]、量子盲签名[12-14]、量子代理签名[15-16]和量子群签名[17-18]等不同应用背景的签名方案，还有一些复杂类型的签名方案，如量子群盲签名[19]、量子代理弱盲签名[20]、量子广播多重盲签名[21]、量子代理多重签名[22]等。量子签名已成为人们研究量子密码学进程中的研究热点。

在诸多类型的签名方案中，目前所见到的大部分方案都是以单用户签名及单用户验证居多，关于多用户签名或多用户验证的签名方案研究得相对较少，尤其是多用户验证。然而在现实生活当中，一份重要的签名文件可能需要多个验证者合作验证签名。

本文提出一种多人验证的量子签名方案。它以三粒子纠缠W态[23]为量子通道，各方的共享密钥采用著名的BB84[24]协议分发，加密均采用一次一密算法和量子单向函数，以确保信息的安全发送。利用量子信息拆分（quantum information splitting）的思想（即秘密信息的拥有者通过量子方法将信息分成若干部分，发送给每个参与者，以至于只有所有的参与者一起才能够重新恢复出秘密消息）达到多人验证的目的。签名算法确保了经典安全性，为了检测是否存在窃听者，在粒子的分发过程中还随机插入了诱骗光子[24-25]确保传输的安全，更能抵御不诚实的攻击者的截获重发攻击与纠缠附加粒子攻击。最后，通过比较分析，提出的多人验证签名方案比一些已提出的量子签名方案在效率和安全性上都有所提高。

2 基于W态的量子信息拆分

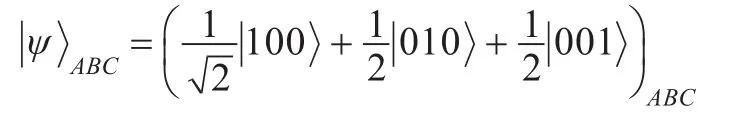
假设粒子A，B，C处于3量子比特W态：其中粒子A属于发送者Alice，粒子B，C分别属于接收者Bob1和Bob2，这里假设Bob1和Bob2至少有一个是诚实的。设Alice要共享的未知量子态为=+。

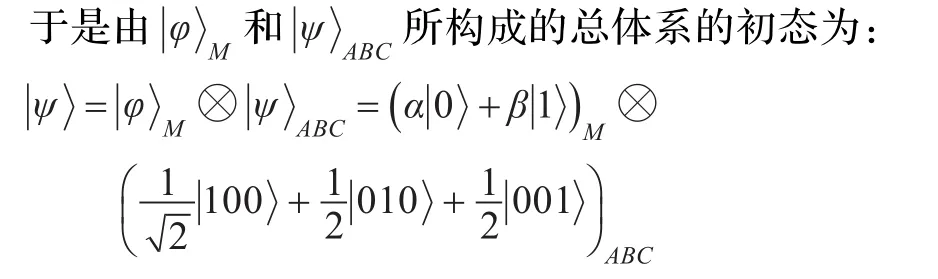
Alice对粒子M与粒子A作Bell测量，结果将等可能地塌缩为下面的式子之一：

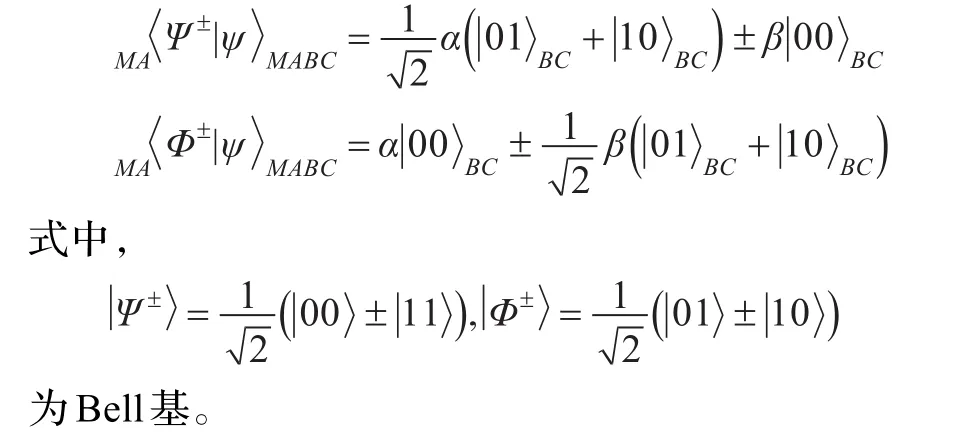
Alice通过经典信道告诉Bob1和Bob2与上述测量结果所对应的2比特的经典信息，对应规则如下：

显然，Bob1和Bob2不能通过对各自的粒子作局域操作恢复粒子M的量子态，为了重新恢复粒子M的量子态，Bob1和Bob2只能根据上述经典信息对他们手上的粒子B、C做联合幺正变换，即如果Bob2同意让Bob1恢复原始量子态的话，则他们作以下联合变换：

反之，如果Bob1同意让Bob2恢复原始量子态的话，则他们作以下联合变换：

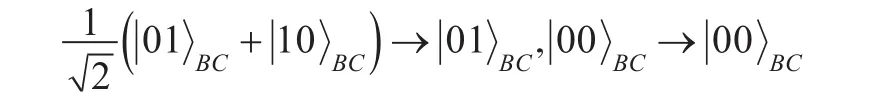
3 签名算法

签名的过程包括三个阶段：初始化阶段、签名阶段和验证阶段。参与者包括签名人Alice和验证人Bob1，Bob2（这两个验证人至少有一个是诚实的）。方案实施的直观过程如图1所示。

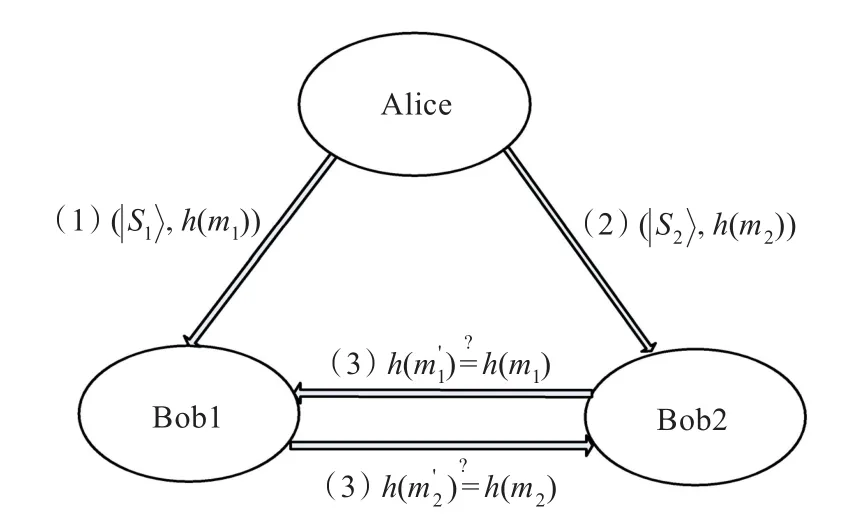
图1 多人验证签名的直观模型

3.1 初始化阶段

（1）假设Alice要签名的消息是m={m(1)，m(2)，…，m(n)}，i=1，2，…，n，将m分成m1和m2两部分，其中：m=m1⊕m2，“⊕”为异或运算。例如：对于n=6，分别有：m={011001}，m1={110010}，m2={101011}。

（2）根据m1和m2，Alice制备两份相应的量子态：

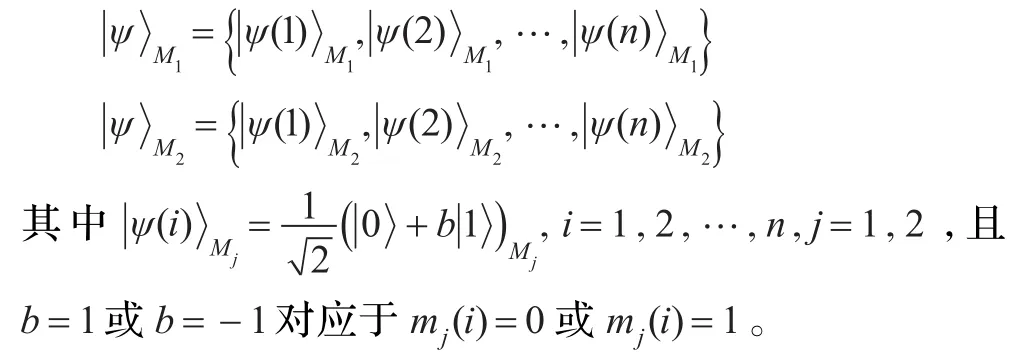
（3）Alice与Bob1通过无条件安全的BB84[24]协议共享2n-bit密钥KAB1，同样地，Alice与Bob2共享2n-bit密钥KAB2。

（4）Alice制备两组处于相同三粒子纠缠W态的序列，假设为：

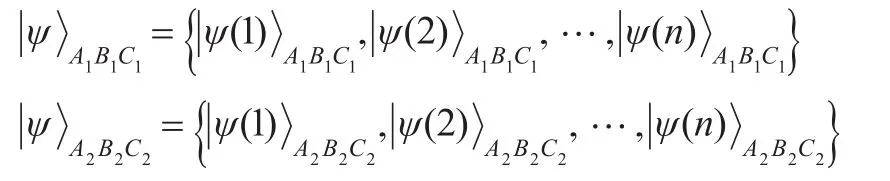
得到如下粒子序列：

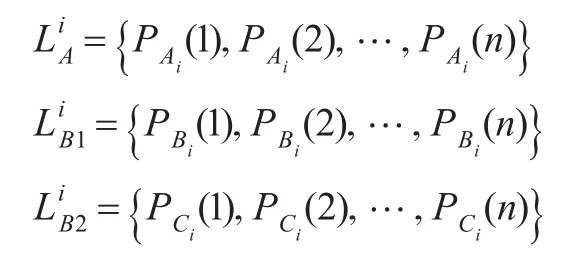
其中i=1，2。

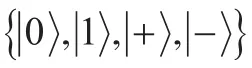
3.2 签名阶段

（3）Alice将(S1，h(m1))和(S2，h(m2))分别发送给Bob1和Bob2，这里h是指hash函数，h(m1)和h(m2)均为k位。

3.3 验证阶段

（1）Bob1收到(S1，h(m1))之后，首先用密钥KAB1解密S1得 βM1A1，根据 βM1A1和第2章中的量子信息拆分原理，Bob1在Bob2的帮助下对他们的粒子PB1(i)与PC1(i)作联合幺正变换。然后Bob1对自己的粒子PB1(i)作相应

（2）同样地，Bob2收到(S2，h(m2))之后，首先用密钥KAB2解密S2得 βM2A2。根据 βM2A2和第2章中的量子信息拆分原理，Bob2在Bob1的帮助下对他们的粒子PC2(i)与PB2(i)作联合幺正变换，然后Bob2对自己的粒子(i)作相应的幺正变换，可以重新恢复。最后Bob2用基测量粒子序列得，比较h()及h(m2)，若相等，则继续下面的验证，否则的话，终止验证。

4 安全性分析

4.1不可伪造性

假设敌手Eve想要冒充Alice对某消息m进行签名，他截取了Alice发送给Bob1和Bob2的粒子，自己制备新的2n个三粒子W态，将每个W态中的两个粒子分别发送给Bob1和Bob2，这种攻击虽然没有破坏三重态粒子对的纠缠性，但Eve也肯定不能取得成功。因为他没有Alice与Bob1和Bob2的共享密钥KAB1和KAB2，且从本方案公布的参数(S1，S2，h(m1)，h(m2))中，Eve无法获取密钥KAB1和KAB2，尤其是当通信者采用一次一密方式和量子单向函数加密时，系统将是无条件安全的，因此Eve无法对测量结果进行加密，这样就很容易被Bob1和Bob2识破。即使是发生了最坏的情况，比如说密钥KAB1和KAB2泄漏给了Eve，他仍然不能冒充Alice进行签名，因为Alice发送给Bob1和Bob2的粒子序列和中加入了诱骗粒子，而非正交态粒子是不可区分的，诱骗态的位置只有Alice知道，在Bob1和Bob2收到粒子序列之后，Alice才会公布这些插入的非正交态粒子的位置和测量基。所以，Eve不能伪造消息m及签名(S1，S2)。

假设签名验证者Bob1是不诚实的，他想要伪造Alice的消息和签名，在此之前，已经假设Bob1和Bob2中至少有一个人是诚实的，因此Bob2一定是诚实的。在签名算法的验证阶段，Bob1需要解密S1得到 βM1A1，并根据 βM1A1对自己手上的粒子序列作相应的幺正变化后再用基测量这个粒子序列，得到m1'，似乎Bob1已经可以任意地篡改消息m1'和签名S1了，但是他不知道Bob2通过测量得到的，而最有可能Bob1能够得到的攻击方式是纠缠附加粒子攻击（即通过某种方法将自己的量子比特和Bob2的量子比特相纠缠，从而相干地测量处理这些量子比特来非法获取信息），但本文采取的诱骗态技术能够很好地防止这种攻击方式。假设Bob1通过局域酉操作作用在Hilbert空间HBob1⊗HBob2上，Bob1的攻击对诱骗态的影响如下：

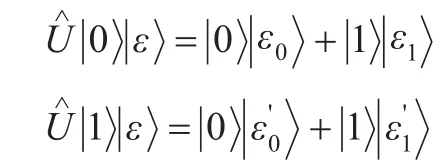
4.2 不可否认性

Alice不能否认她对消息m的签名。因为Alice需要发送签名(S1，S2)给Bob1和Bob2，其中用到的加密密钥KAB1和KAB2只有Alice与Bob1和Bob2知道，且没有Alice对自己粒子的Bell基测量结果，Bob1和Bob2不可能进行对签名的验证。

签名验证人Bob1和Bob2均不能否认收到Alice的签名。一方面，因为在验证签名(S1，S2)时，需要先用解密密钥KAB1和KAB2对(S1，S2)解密，这说明Bob1和Bob2是签名算法的参与者。另一方面，在签名算法的验证阶段，最后要验证h()h(m1)及h()h(m2)，有一种可能是不诚实的Bob1明明收到了来自Alice的签名，却否认这一事实，即Bob1宣布h()≠h(m1)，那么签名(S1，S2)不被接受。但作为诚实方的Bob2不会接受这一结果，因为是他协助Bob1完成对签名S1的验证。同样地，如果Bob2是不诚实的，他也不能否认接收了签名。

5 效率分析

这里，对N比特消息签名时所需要的传输量子比特数为指标来比较几种量子签名协议的效率。文献[5]定义签名效率为η=Bs/(Qt+Bt)，其中Bs表示签名消息比特数，Qt表示协议中传输的量子比特数，Bt表示协议中传输的经典比特数。

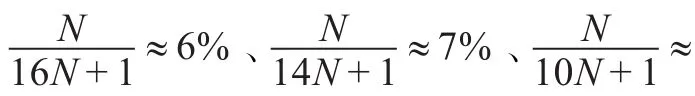
此外，文献[2，6-7]所提出的签名方案，是在一个仲裁者的监督下完成对未知量子态的签名和验证，但这三个方案均不能同时满足安全性要求的不可伪造性和不可否认性。本文提出的方案是在两个验证者相互监督的情况下完成对签名的验证，并且方案能够同时保证不可伪造性和不可否认性。本文与Gottesman和Chuang提出的量子签名协议[1]虽然都是多人验证签名方案，Gottesman和Chuang的方案在每签名1-bit的消息时要产生多个公钥的副本并在签名后被丢弃。而本文的方案，签名N-bit的消息，只需要制备2N个三粒子W态，共享4N比特的密钥。相比之下，本文的方案效率明显比Gottesman和Chuang的要高很多，复杂度也较低。

综上分析，得到效率比较表如表1所示。

表1 各量子签名的效率 （%）

相比之下，本文的方案较之前所提出的一些量子签名方案，协议的效率和安全性都有所提高。

6 结束语

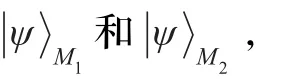
[1]Gottesman D，Chuang I.Quantum digital signatures[EB/OL]. [2014-01-04].http：//arxiv.org/abs/quant-ph/0105032.

[2]Zeng G H，Christoph K.Arbitrated quantum-signature scheme[J].Physical Review A，2002，65（4）：1-6.

[3]Lee H，Hong C，Kim H，et al.Arbitrated quantum signature scheme with message recovery[J].Physics Letters A，2004，321（5）：295-300.

[4]Lu X，Feng D G.Quantum digital signature based on quantum one-way functions[EB/OL].[2014-01-04].http：//arxiv. org/abs/quant-ph/0403046.

[5]王剑，张权，唐朝京.针对经典消息的高效量子签名协议[J].通信学报，2007，28（1）：64-68.

[6]Li Q，Chan W H，Long D Y.Arbitrated quantum signature scheme using Bell states[J].Physical Review A，2009，79（5）：1-4.

[7]Zou X F，Qiu D W.Security analysis and improvements of arbitrated quantum signature schemes[J].Physical Review A，2010，82（4）：1-10.

[8]李伟，范明钰，王光卫.基于纠缠交换的仲裁量子签名方案[J].物理学报，2011，60（8）：1-7.

[9]Wen X J，Liu Y，Sun Y.Quantum multi-signature protocol based on teleportation[J].Zeitschrift fur Naturforschung A，2007，62（3/4）：147-151.

[10]温晓军，刘云.一种可实现的量子有序多重数字签名方案[J].电子学报，2007，35（6）：1079-1083.

[11]杨亚涛，薛霆，李子臣.广播多重量子数字签名方案的设计与分析[J].中国科学技术大学学报，2011，41（10）：924-927.

[12]Wen X J，Niu X M，Ji L P，et al.A weak blind signature scheme based on quantum cryptography[J].Optics Communications，2009，282（4）：666-669.

[13]温晓军，田原，牛夏牧.一种基于秘密共享的量子强盲签名协议[J].电子学报，2010，38（3）：720-724.

[14]Wang M M，Chen X B，Yang Y X.A blind quantum signature protocol using the GHZ states[J].Science China Physics，Mechanics and Astronomy，2013，56（9）：1636-1641.

[15]常祖领，周景贤，张劼，等.基于EPR态的量子代理签名方案[J].计算机应用研究，2010，27（2）：675-677.

[16]Zhou J X，Zhou Y J，Niu X X，et al.Quantum proxy signature scheme with public verifiability[J].Science China Physics，Mechanics and Astronomy，2011，54（10）：1828-1832.

[17]温晓军，蔡学军.一种基于量子纠缠态的群签名协议[J].计算机应用研究，2011，28（9）：3524-3526.

[18]Zhang K J，Song T T，Zuo H J，et al.A secure quantum group signature scheme based on Bell states[J].Physica Scripta，2013，87（4）：1-5.

[19]Xu R，Huang L S，Yang W，et al.Quantum group blind signature scheme without entanglement[J].Optics Communications，2011，284（14）：3654-3658.

[20]陈永志，刘云，温晓军.一个量子代理弱盲签名方案[J].量子电子学报，2011，28（3）：341-349.

[21]Tian Y，Chen H，Ji S，et al.A broadcasting multiple blind signature scheme based on quantum teleportation[EB/OL]. [2014-01-04].http：//link.springer.com/article/10.1007/s11082-013-9785-y.

[22]Cao H J，Wang H S，Li P F.Quantum proxy multi-signature scheme using genuinely entangled six qubits state[J]. International Journal of Theoretical Physics，2013，52（4）：1188-1193.

[23]Zheng S B.Splitting quantum information via W states[J]. Physical Review A，2006，74（5）：1-4.

[24]Bennett C H，Brassard G.Quantum cryptography public key distribution and coin tossing[C]//Proc of IEEE International Conference on Computers，Systems and Signal Processing.India：Banglore Press，1984：175-179.

[25]Tan X Q，Jiang L X.Improved three-party quantum secret sharing based on Bell states[J].International Journal of Theoretical Physics，2013，52（10）：3577-3585.

ZHANG Qiong,TAN Xiaoqing

Department of Mathematics,College of Information Science and Technology,Jinan University,Guangzhou 510632,China

A multi-verifiers signature scheme using W state is proposed.Based on quantum information splitting,the protocol splits the information into two parts and encrypts them by on-time pads and quantum one-way function.Two verifiers verify the signature.The scheme not only satisfies the security requirements of unforgeability and non-repudiation,but also resists the attack strategies of intercept resend attack and entanglement measure attack.The efficiency and the security are both improved compared with other quantum signature schemes.

quantum information splitting;W state;quantum signature;multi-verifiers;decoy states

提出了一种利用W态实现的对经典信息的多人验证签名方案。协议基于量子信息拆分原理，将签名信息拆分成两部分，由一次一密算法和量子单向函数加密签名信息，两个验证人验证签名。方案满足经典安全性要求的不可伪造性和不可否认性，同时也能够抵御量子攻击策略当中的截获重发攻击和纠缠附加粒子攻击，相较其他量子签名方案，效率和安全性都有所提高。

量子信息拆分；W态；量子签名；多验证人；诱骗态

A

TP309

10.3778/j.issn.1002-8331.1403-0183

ZHANG Qiong,TAN Xiaoqing.Multi-verifiers signature scheme based on quantum information splitting.Computer Engineering and Applications,2014,50（24）：65-69.

国家自然科学青年基金项目（No.61003258）。

张琼（1990—），女，硕士研究生，研究领域：密码编码学；谭晓青（1976—），通讯作者，女，博士，副教授，研究领域：密码编码学。E-mail：ttanxq@jnu.edu.cn

2014-03-14

2014-04-29

1002-8331（2014）24-0065-05

CNKI网络优先出版：2014-07-11，http∶//www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1403-0183.html