粘胶短纤维的干燥特性及其动力学模型研究

王瑞利，李 慧，张 军

(1.黄河科技学院工学院，河南郑州450006;2.郑州大学化工与能源学院，河南郑州450001)

粘胶纤维作为一种常见而又重要的化工原材料，在工业生产和日常生活中得到广泛的使用。粘胶纤维的干燥过程耗能较大，为了提高经济效益，生产环节绿色环保，对粘胶纤维的干燥过程进行理论和实验研究具有重大的意义［1］。

在前期研究中，对粘胶短纤维链板式松弛热定型机内部流场进行了数值模拟，得到了其流场速度和压力分布规律，结合现场测试结果，提出对其匀风板的改进方案，并进行了验证［2－3］;通过粘胶纤维干燥特性实验，分别测定了热风温度、纤维层厚度、热风风速、纤维层含水率等工艺参数对其干燥过程的影响［4］。国内外研究人员对其他不同类型的纤维和干燥形式进行了实验和理论研究，进一步研究粘胶短纤维干燥影响因素，尤其增加对粘胶短纤维热风干燥过程动力学理论分析，从而更好地提高其干燥效率，降低干燥成本是十分必要的。

作者在前期粘胶短纤维干燥特性的实验研究基础上，应用单指数干燥模型和三参数Logaritmic干燥模型，对粘胶短纤维的热风干燥特性进行了理论研究;对实验数据进行回归分析，得到了粘胶短纤维的干燥动力学模型参数，进而得出粘胶短纤维的热风干燥理论计算曲线;并对模型的计算结果与实验结果进行比较，得到更适合分析粘胶短纤维干燥规律的理论模型。

1 纤维干燥实验

1.1 干燥实验装置

为了真实地反应粘胶纤维的干燥过程，自行设计了一种结构简单、测试方便的粘胶纤维干燥实验装置，此实验装置已申请了国家发明专利［5］。从图1可知，该实验装置由空气压缩机、电加热炉、纤维干燥器组成。空气由压缩机输送，进入加热炉被加热到设定温度后流入纤维干燥器。气体流量由调节阀调节，并由转子流量计进行计量。干燥器入口装有温、湿度传感器、压力传感器和气流速度传感器。干燥器出口也安装有温、湿度传感器、压力传感器和气流速度传感器，用以测量干燥器内的空气状况。传感器通过数据线连接到计算机中进行数据处理，可以得到干燥实验过程中测试点的温度、压力、湿度。

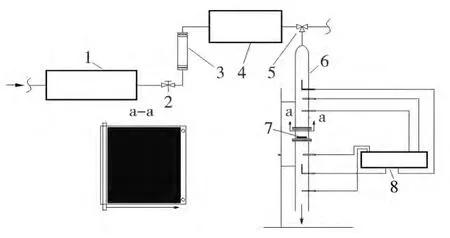
图1 干燥实验装置示意Fig.1 Scheme of drying experimental unit

1.2 实验方法

粘胶纤维由郑州纺织机械有限公司提供;在进行实验前，首先对物料进行预处理。纤维大小由干燥器尺寸确定。

影响纤维干燥的因素设定:纤维厚度(H)分别为90 mm和150 mm;纤维层初始含水率(S)用蒸馏水配制，采用BL200S型电子天平测定物料质量，分别配制S为90% 和170%;热风风速(V)由调节阀控制，分别为 1.2，1.6 m/s，热风温度(T)分别是100，120℃。实验过程采用不同的T和V，对干燥器内的不同S和H的纤维进行干燥测试，每组实验重复5次。

2 纤维干燥动力学模型

为了更好的研究粘胶短纤维的干燥特性，需要选取和建立一个更适合的干燥动力学模型。粘胶短纤维的干燥曲线近似为指数函数，考虑到干燥方程的复杂性和准确度，选取了两种在目前使用较多的干燥动力学模型即单指数方程和三参数Logaritmic 指数方程［6］。

单指数模型:

Logaritmic模型:

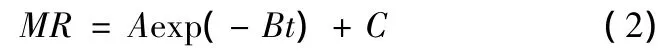
式中:M为纤维含水率;t为干燥时间;R，A，B，C均为待定系数。

实验过程中，选取的影响因素为T，H，V以及S。模型中的影响因子为T，V以及H。而采用的Logaritmic模型中有3个待定的系数A，B，C，那么这3个待定系数就是上面3个影响因素的函数。R表示纤维层的含水率参数，取值为0～1，可通过实验数据拟合得到。为了使方程能够进一步简化，考虑到在实验中纤维主要影响因子是T及V，可以得到以下方程式:

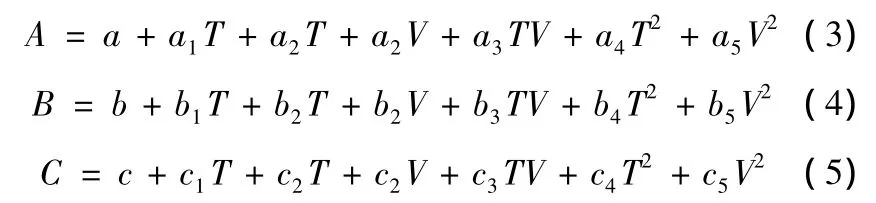
式中:a～a5，b～b5，c～c5均为待定系数。

对实验得出的数据采用最小二乘法进行回归分析，可计算各个系数。

3 结果与讨论

3.1 T对纤维干燥特性的影响

在其他条件一定时，分别选用T为100℃和120℃对纤维层进行干燥。通过对实验结果拟合，选取两个模型的R为0.972。根据公式(3)～(5)分别计算出相应的参数，并由公式(1)和(2)计算出两个模型的纤维干燥曲线即纤维M与t的关系。

从图2可知，随着T的提高，热风传递给纤维层的热量也越多，纤维干燥速率也随之加快。通过两个干燥模型计算结果发现:T为100℃时，干燥时间为150～300 s的干燥阶段，以及T为120℃时，干燥时间为150～250 s的干燥阶段，两个模型描述结果都不能完全接近实验曲线。但从整体来看两个模型计算的曲线都能反映实验过程，尤其在干燥时间为0～150 s的干燥曲线。但比较两个模型计算结果，三参数Logaritmic模型比单指数模型能更接近实验结果。

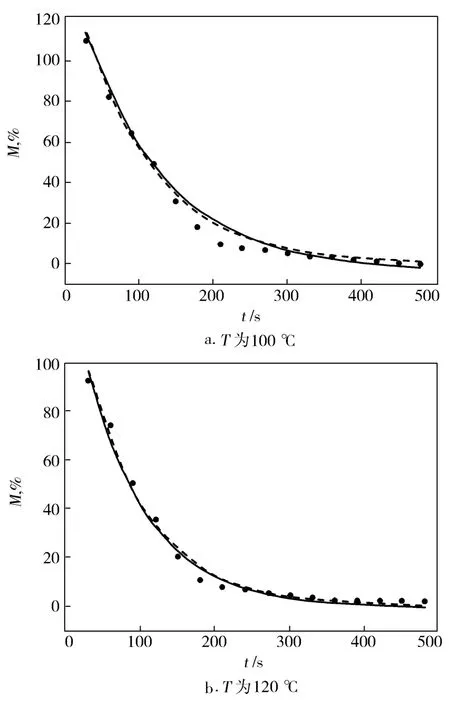
图2 不同T时纤维干燥特性的实验数据与模型计算结果Fig.2 Experimental data and model calculation result on fiber drying behavior at different T

3.2 S对纤维干燥特性的影响

在其他条件一定时，分别选用S为90%和170%来对比其干燥特性的变化。通过对实验结果的拟合，两个干燥模型的R分别相应调整为0.930和0.997，同样，可计算得到两个模型的纤维干燥曲线。

从图3的模型计算结果和实验结果表明:S越高，其干燥速率越慢;对于S为170%的纤维干燥曲线，两个模型计算曲线基本重合，而且这个过程与实验结果吻合较好;对于S为90%的纤维干燥曲线(图3a)，在干燥时间达200 s以后，三参数Logaritmic模型计算结果更接近实验曲线。

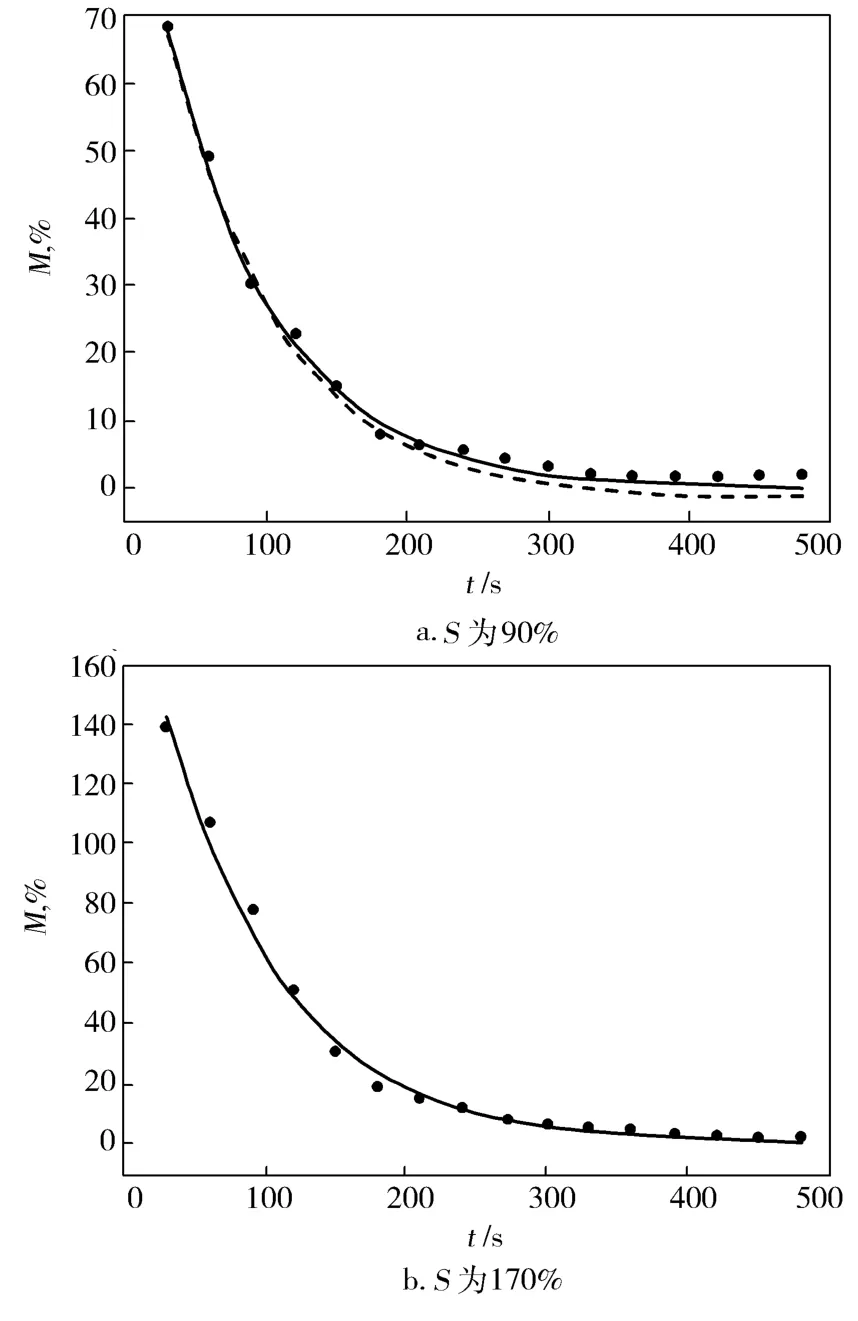
图3 不同S时纤维干燥特性的实验数据与模型计算结果比较Fig.3 Experimental data and model calculation result on fiber drying behavior at different S

3.3 H对纤维干燥特性的影响

在其他条件一定时，分别选用H为90 mm和150 mm进行实验。根据实验条件，通过调整计算拟合得到两个干燥模型的R为0.972，同样可计算得到两个模型的纤维干燥曲线。从图4可以看到:在不同H实验条件下，两个干燥动力学模型的计算结果与实验结果非常相近，两个模型计算的纤维干燥曲线与实验曲线几乎重合，并且两个模型都能很好地描述实验过程;但对H为150 mm的干燥曲线，三参数Logaritmic模型的计算结果在整个曲线更接近实验结果，这也说明三参数的Logaritmic模型能更好地描述纤维的干燥特性。

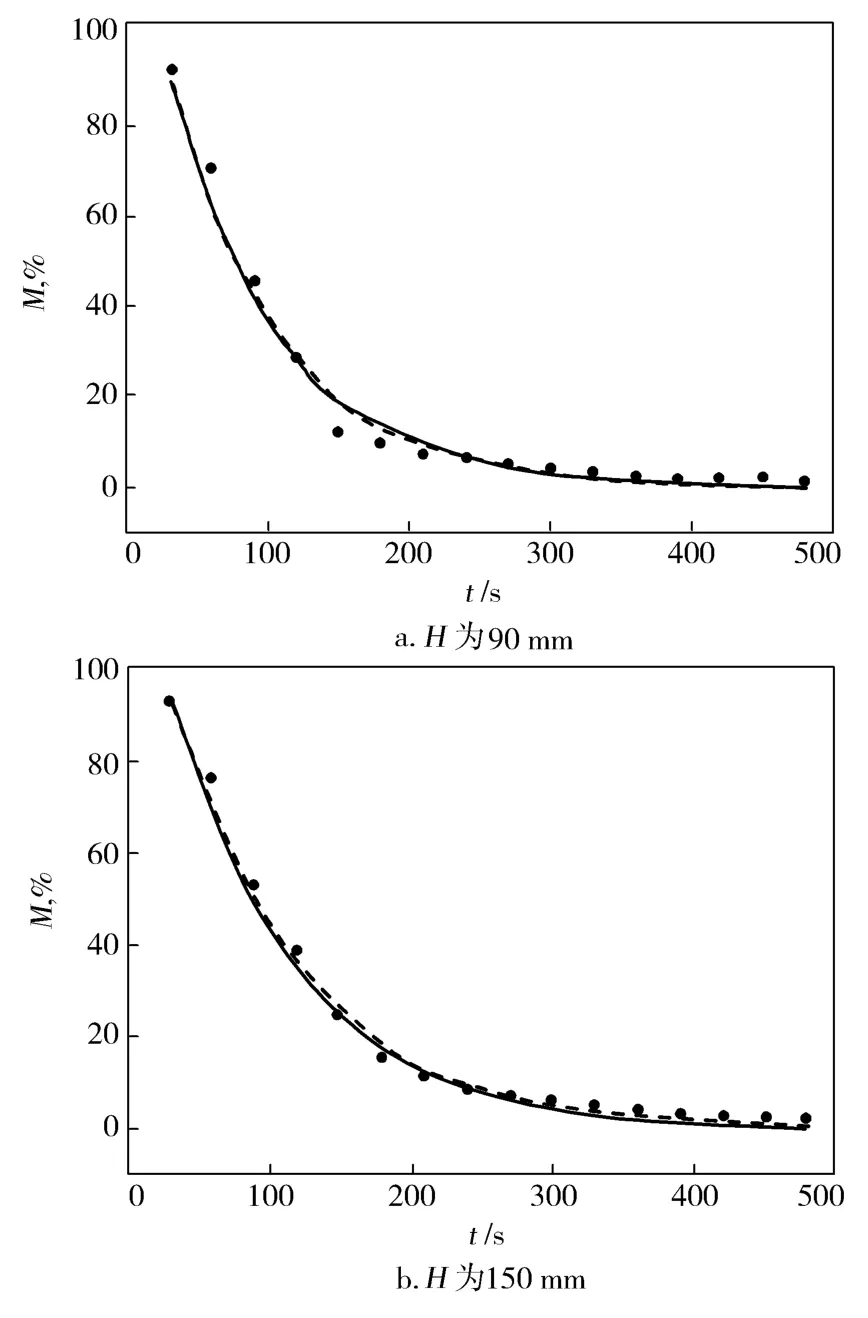
图4 不同H时纤维干燥特性的实验数据与模型计算结果Fig.4 Experimental data and model calculation result on fiber drying behavior at different H

3.4 V对纤维干燥特性的影响

在其他条件一定时，选用V分别为1.2 m/s和1.6 m/s进行实验。根据此实验条件，计算拟合得到两个模型的R为0.972。从图5可以看出:两个模型对不同V时纤维干燥曲线的描述都有误差;V为1.2 m/s时，三参数Logaritmic模型计算结果在干燥时间为200 s之前与实验结果接近，而单指数模型计算的曲线在干燥时间达300 s之后与实验结果接近;热风风速1.6 m/s时，两个模型在干燥时间小于200 s的计算结果与实验结果接近，而干燥时间大于200 s，三参数Logaritmic模型计算结果与实验结果更接近。

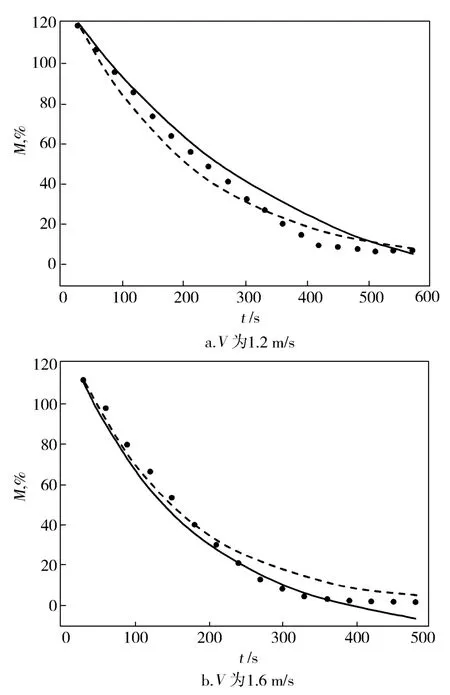
图5 不同V时纤维干燥特性的实验数据与模型计算结果Fig.5 Experimental data and model calculation result on fiber drying behavior at different V

通过实验和理论模型计算结果对比分析可知，三参数的Logaritmic模型精度明显高于单指数模型，因为Logaritmic模型相对于单指数模型多考虑了一个参数，所以Logaritmic模型能更好研究和预测粘胶短纤维的干燥特性。

4 结论

a.干燥过程中，T，H，V，S对粘胶短纤维的干燥特性都有着重要的影响。粘胶短纤维的干燥特性曲线近似为一指数函数。

b.选用了两参数的单指数模型和三参数的Logaritmic模型对纤维的干燥特性进行了分析，在干燥时间为150～300 s的阶段，两个模型描述结果都不能很好地反映实验结果。对于不同S和H条件下，两个干燥模型的计算结果都非常相近;对于不同T和V时，两个模型对纤维干燥曲线的描述都有误差，三参数的Logaritmic模型计算结果与实验结果更接近。因此，三参数的Logaritmic模型能更好分析粘胶短纤维的干燥特性。

［1］ 陈志华.纺织行业的低碳经济路径［J］.南通纺织职业技术学院学报，2010，10(2):69 －72.

［2］ 张军，常佳，魏新利，等.短纤维链板式松弛定型机流畅研究［J］.合成纤维工业，2010，33(5):55 －58.

［3］ 李慧，张军，常佳，等.短纤维链板式松弛热定型机内部流场测试及数值模拟［J］.合成纤维工业，2012，35(1):67－71.

［4］ 张军，李慧，简士钊.粘胶短纤维干燥特性的影响因素研究［J］.合成纤维工业，2013，36(5):13 －16.

［5］ 张军，魏新利，简士钊，等.纤维干燥实验测试装置:中国，201010287743.3［P］.2012 －05 －30.

［6］ Mathioulakis E，Karathanos V T，Belessiotis V G.Simulation of air movement in a dryer by computational fluid dynamics:Application for the drying of fruits［J］.J Food Eng，1998，36(2):183－200.