一种基于效益的多机器人避碰协调策略

姚芝凤，叶秀芬，戴学丰，朱 玲，孙 明

(1.齐齐哈尔大学计算机与控制工程学院,黑龙江 齐齐哈尔 161006；2.哈尔滨工程大学自动化学院,黑龙江 哈尔滨 150001)

1 引言

一般来说，移动机器人在特定的环境中作业时都需要一个地图，因此采集必要的信息完成地图的构建是移动机器人自主导航的关键[1]。在未知环境下的地图创建，由于缺少全局信息，SLAM(Simultaneous Localization And Mapping)算法得到了广泛的研究。近二十年来，单机器人的SLAM算法，包括地图的表示方法、数据关联和对不确定性的处理等方面都取得了很大的成就[2～7]。但是，在动态、复杂和大环境中执行环境探索任务时，单机器人系统和多机器人系统相比，存在探索效率低，鲁棒性较差，以及单机器人没有能力完成某些任务的问题[8]。因此，近年来多机器人系统的SLAM算法成为研究热点。

多机器人系统的SLAM问题，除了包括单机器人系统SLAM中涉及到的地图表示方法、数据关联和对不确定性的处理之外，还包括控制结构的选择、机器人间的协调、相互定位和子地图融合等方面的问题[9]。其中，机器人间的协调是多机器人系统完成任务的关键，而协调包括机器人在执行任务时避免和其它机器人的碰撞，也就是避碰协调问题。

一些避碰协调策略可以用来解决避碰协调问题，包括基于广义势场的多机器人避碰算法[10]；基于协商和意愿强度的多机器人避碰协调协作算法[11]。但是，这类算法主要是基于反应行为的避碰协调，即绕开静止的障碍物，而本文所说的避碰协调是避免机器人之间的碰撞[1]，机器人面对的障碍物是其它机器人，是可移动的。因此，需要对避免机器人之间碰撞的避碰协调算法进行单独研究或对避碰协调策略进行改进。以无交通灯的交叉路口为模型的避碰协调算法[12]，针对的是避免机器人之间的碰撞，但该算法不是以提高多机器人系统探索效率为主的避碰协调算法。而在多机器人协作完成地图构建时，一个主要的性能指标是在尽可能短的时间内获得尽可能多的信息[1]，因此交叉路口通过优先权的确定，不应该单考虑时间方面，还要考虑每个机器人之间的效益是不同的，从而提高多机器人系统探索地图的效率。

本文提出的基于效益的多机器人避碰协调算法，其中效益包括两个部分：代价和效用。代价是指机器人从当前位置到达目标点的距离；效用是指机器人到达目标位置，能观测到的信息增益。该算法是以提高多机器人系统整体探索效率为主的避碰协调算法，而不是具有最大效益的机器人具有最高的交叉路口通过优先权的方案。本文的结构如下：第2节给出了基于代价-效用的机器人效益模型；第3节讨论了基于效益的多机器人避碰协调算法；第4节给出了一个仿真示例，并对仿真结果进行了相应的分析和说明；第5节为结束语。

2 基于代价-效用的效益模型

本文地图探索任务分配采用的是基于市场经济的分布式任务分配方法。地图采用是栅格地图的表示方法。

基于市场经济的分布式任务分配方法[13,14]，首先分配给每个机器人一组目标，然后机器人通过拍卖标的的方法与其它机器人对目标进行协商。栅格地图，根据占用的概率的不同，分为未被占用、占用和未知三种情况[15]。这样，机器人可以利用边界单元格来界定已探索和未探索的区域，从而到达没有被探索的地方。基于市场经济的分布式任务分配方法在采用栅格地图表示时，模型的效益是效用减去代价，代价是从机器人当前位置到达要探测目标的距离的估计值，效用是机器人在到达探测目标这段距离中，可探索到的未被探索栅格的数目。

由于本文主要研究的是机器人之间的避碰协调策略，而基于市场经济的分布式任务分配方法中，具体的竞标和任务分配过程不是本文的主要研究内容。因此，作者在这里直接假设竞标和任务分配已经很好地完成了，而仅仅考虑的是具体任务分配后的效益模型，也就是机器人已经确定了探测目标后到达该目标的效益。假设由n个机器人构成的多机器人系统，则第i个机器人的基于代价-效用效益模型可以直接表示如下：

Bi=Ui-αCi

(1)

其中，i∈Z+,1≤i≤n，Bi表示第i个机器人效益函数，Ui表示第i个机器人效用函数，Ci表示第i个机器人代价函数，α为Ui和Ci之间的权重系数。

3 基于效益的多机器人避碰协调算法

在考虑机器人发生碰撞时，由于存在等待时间的问题，因此公式(1)中的Bi变为Bi(k)：

(2)

其中，ti是机器人Ri不考虑等待时间直接到达目标栅格的行走时间，Bi(k)为机器人Ri的不同交叉路口通过顺序时的单位时间效益，Δti(k)表示机器人Ri在交叉路口的等待时间。机器人Ri的交叉路口通过顺序不同，则其在交叉路口的等待时间Δti(k)就不同。例如，Ri最先通过，则Δti(0)的值为零；如果Ri的通过顺序为第二，则Δti(1)的值就有可能不为零；若Ri的通过顺序为第三，如果之前通过的两个机器人不完全相同，则可能产生不同值的Δti(2)和Δti(3)。衡量n个机器人系统效率的单位时间效益为：

(3)

由于机器人通过交叉路口的顺序不同，则机器人Ri的等待时间Δti(k)的值不同，由公式(2)得到的机器人Ri的单位时间效益Bi(k)就不同，因此由公式(3)得出的n个机器人单位时间效益B(k)也不同。

本文提出的基于效益的多机器人避碰协调算法，不是具有最大效益的机器人具有最高的交叉路口通过优先权，而是能使多机器人系统单位时间效益最大化，也就是最能提高多机器人系统效率的避碰协调方案决定机器人的交叉路口通过的优先权，即由B决定的。

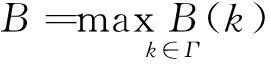
(4)

在执行该避碰协调算法时，首先给出该算法要协调的机器人的约束条件：其一是要通过但还没通过该交叉路口的机器人；其二是与交叉路口的距离满足一定的条件，这里设定一个距离阈值D(也可设时间阈值T，即D与机器人速度的比值)，当与交叉路口的距离小于或等于距离阈值D时，同时满足前一个约束条件的机器人为避碰协调算法要协调的机器人。

其次，选择临时主机运行避碰协调算法，选择过程也是采用竞标的方法，选择在不考虑等待时间Δti(k)时，具有单位时间效率最小的机器人获得标的，作为交叉路口D范围内的局部区域的临时主机，对通过交叉路口的机器人的通过顺序进行计算。当临时主机通过交叉路口后，再次根据等待单位时间效率最小的原则，选择新的临时主机。选择具有单位时间效率最小机器人作为临时主机的主要原因是，在本文提出的避碰协调算法中，一般具有最大单位时间效率的机器人有可能最先通过，通过后就不满足进入避碰协调算法的条件，这样就会出现频繁换主机的情况。算法的实现过程如下：

首先，根据避碰协调算法要协调的机器人的约束条件得到所有要协调的机器人。

然后，利用竞标方法根据等待单位时间效率最小的原则选择临时主机，临时主机利用穷举法(因为避碰协调算法同时协调的机器人不会很多，所以可以采用穷举法)得到所有通过交叉路口顺序的排列组合(也可采用冒泡法，例如先任意选择两个机器人R1和R2产生两个排列组合，进行一次比较，选择单位效益最大的一组，假如R1R2较好；然后R3加入，只需对R3R1R2、R1R3R2和R1R2R3进行计算比较，假如得到的通过顺序为R2R1R3时较好；再加入R4时，需对排列为R4R2R1R3、R2R4R1R3、R2R1R4R3和R2R1R3R4再进行比较，仿真示例中用的是该方法)。

最后，对不同的排列组合根据公式(2)计算各个机器人的单位时间效益，再根据公式(3)进行加和，根据公式(4)选择单位时间效益总和最大的排列组合为最终的交叉路口通过顺序。简单的流程如图1所示。

Figure 1 Flow chart of collision avoidance algorithm图1 避碰协调算法流程图

4 仿真示例及结果分析

为了对所提出的避碰协调策略进行说明，本节给出了一个仿真示例，假设根据基于市场经济的分布式任务分配方法已经完成了竞标和任务分配的过程，也就是已经确定了各机器人的探测目标和相应的效益。在初始时刻t0时，机器人R1、R2、R3和R4的相关参数如表1所示。

t0时刻R1、R2、R3和R4的位姿及目标点T1、T2、T3和T4的位置如图2所示。

图2中，黑色的方块代表机器人，黑色的实线圆圈代表直径Dc为600 cm的交叉路口(Cross)，黑色的实心小圆圈代表各机器人已经确定的目标点，黑色的点划线大圆圈表示根据距离阈值D确定的避碰协调算法要协调的机器人的所在范围。距离阈值D如果选择得太大，算法需要处理的机器人数目过多，计算过于复杂；如果D选择得过小，算法处理的机器人太少，则降低协调的作用。因此，D的选择需要大量的实验验证，这里假设得到的最佳的D值为交叉路口直径Dc的2倍即1 200 cm。因此，距离交叉路口的距离小于1 200 cm，且要经过此交叉路口的机器人确定为算法要协调的机器人。本示例中，R1、R2、R3和R4在t0时刻距离交叉路口的距离分别为dR1=1000 cm、dR2=1000 cm、dR3=707 cm和dR4=1414 cm，可知在t0时刻，避碰协调算法要协调机器人为R1、R2和R3。

Table 1 Parameters related robots and targets表1 和机器人及目标点相关的参数

Figure 2 Current pose of robots and position of targets图2 机器人的当前位姿和目标点的位置

避碰协调算法对于该仿真的具体实现过程如下：

(1)根据无等待单位时间效率最小的原则，即第3节的公式(2)，令第i个机器人的等待时间Δti(k)=0，行走时间ti=dRiTi/vRi，效益Bi的取值如表1所示，由公式(2)计算得到最小的Bi(k)。其中，dRiTi是第i个机器人与第i个目标点的距离，vRi是第i个机器人的行走速度，其中i的取值为1、2和3。求得的B1(k)=1.10，B2(k)=1.33，B3(k)=0.35。因此，在t0时刻R3充当临时主机。

(2)先任意选择两个机器人R1和R2产生两个通过交叉路口顺序排列组合为R1R2和R2R1。当顺序为R1R2时，则R1无需等待，即在第3节的公式(2)中Δt1(1)=0，求得B1(1)=1.10/s，而R2则需要等待的时间为Δt2(1)=(dR1+Dc)/vR1-(dR2-Dc)/vR2，求得Δt2(1)=5 s，则B2(1)=1.00/s，由第3节公式(3)得B(1)=B1(1)+B2(1)，因此B1=2.10/s。同样的方法求得顺序为R2R1时，B(2)=2.21/s，因此仅考虑R1和R2时，由第3节公式(4)得到较好的通过顺序是R2R1。类似地，当仅考虑R1和R3时，较好的顺序是R1R3(若得到的较好顺序是R3R1，则需要再选择R2和R3的较好顺序，才能最终确定R1R2R3的最佳通过顺序)，因此可以确定R1、R2和R3的最佳通过顺序是R2R1R3。

在t1时刻，发现机器人R4进入避碰算法的协调范围，可得t1=(t0+4.28) s，如图3所示。

Figure 3 Order calculation of across intersection including R4图3 R4进入了交叉路口通过顺序的计算

由于避碰协调算法在处理R4之前的最佳顺序是R2R1R3，于是R4的加入，临时主机R3只需对排列为R4R2R1R3、R2R4R1R3、R2R1R4R3和R2R1R3R4时的单位时间效益进行计算即可。由此可见，当有新的机器人添加时计算量的增加量并不大。从中得到最大单位效益时的通过顺序为R2R1R3R4，仍然是R2最先通过，如图4所示。

Figure 4 R2 across intersection图4 R2通过交叉路口

机器人一旦通过交叉路口，则从避碰协调算法中移除。例如，R2最先通过交叉路口，则从避碰协调算法中移除R2，如图5所示。

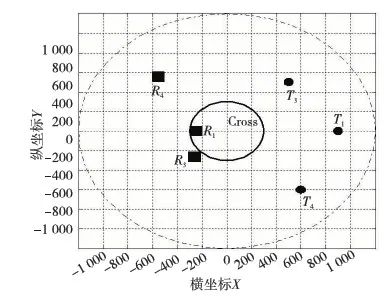
Figure 5 R1 across intersection and remove R2图5 R1通过交叉路口并移除R2

说明，本文假设的当前机器人R1、R2、R3和R4及目标T1、T2、T3和T4的空间位置，是由市场经济任务分配得到的结果，当是异构多机器人系统时，即每个机器人装备的传感器不同，以及各机器人的大小不同时，能完成不同要求的探索任务，存在这种分布情况。

例如，到达目标T2的过程中，存在狭窄的通道，仅R2能通过等，这些方面的约束是在任务分配时所要考虑的。由于考虑的是动态避碰协调过程，接下来将是R1被移除，然后是R2被移除，也有可能有其它的机器人R5、R6和R7等加入避碰协调算法中，并再次选择临时主机，但整个过程的计算量不大，且多机器人系统的整体效率能得到提高。

5 结束语

本文提出了一种基于效益的多机器人避碰协调算法，能够较好地提高多机器人系统探索地图的效率。给出了假定根据基于市场经济的分布式任务分配的方法，完成竞标和任务分配过程后，机器人已经确定了探测目标和相应效益的机器人避碰协调的仿真示例，并对结果进行了相应的分析和说明。

目前的基于市场经济的多机器人系统的任务分配方法，在任务协商时，也没有考虑由于机器人多次避碰协调的等待时间问题，这样会造成任务的分配不够合理。因此，在接下来的工作中，要完成的是在任务分配过程中考虑避碰协调等待时间的基于市场经济分布式任务分配的方法。

[1] Miguel J, Arturo G, Oscar R. A comparison of path planning strategies for autonomous exploration and mapping of unknown environments [J]. Autonomous Robots, 2012, 33(4):427-444.

[2] Zou Zhi-rong, Cai Zi-xing, Chen Bai-fan. Hybrid approach of data association in mobile robot slam [J]. Journal of Chinese Computer Systems, 2011, 32(7):1340-1343.(in Chinese)

[3] Fang Fang, Ma Xu-dong, Dai Xian-zhong. New monte carlo algorithm for mobile robot self-localization [J]. Journal of Southeast University, 2007, 37(1):40-44.(in Chinese)

[4] Dai Bo, Xiao Xiao-ming, Cai Zi-xing, et al. A new environmental modeling method for mobile robot based on laser radar [J]. Machine Tool & Hydraulics, 2007, 35(1):14-18.(in Chinese)

[5] Shang Wen,Ma Xu-dong,Dai Xian-zhong.Mobile robot self-localization based-on multi-sensory information fusion [J]. Journal of Southeast University, 2004, 34(6):784-788.(in Chinese)

[6] Sun Feng-chi, Huang Ya-lou, Kang Ye-wei. Review on the achievements in simultaneous localization and mapping for mobile robot based on vision sensor [J]. Control Theory & Applications, 2010, 27(4):488-493.(in Chinese)

[7] Zhang Xue-xi, Yang Yi-min. Global map building based on omni-vision for mobile robot [J]. Computer Measurement & Control, 2011, 19(3):643-646.(in Chinese)

[8] Liu Li-mei, Cai Zi-xing. Study on map merging for multi-robots [J]. Journal of Chinese Computer Systems, 2012, 33(9):1934-1937.(in Chinese)

[9] Cai Zi-xing. Synergy principles and technologies of multi-mobile robots [M]. Beijing:National Defence Industry Press, 2011.(in Chinese)

[10] Zhao Dong, Zheng Shi-xiong. Multi-robot collision avoidance algorithm based on generalized potential field [J]. Journal of South China University of Technology, 2010, 38(1):124-127.(in Chinese)

[11] Wang Shuo, Tan Min. Multiple autonomous mobile robots avoidance based on negotiation and intention strength [J]. High Technology Letters, 2001, 11(10):70-73.(in Chinese)

[12] Pan Wei. Research on map building of multiple mobile robots [D]. Changsha:Central South University, 2009.(in Chinese)

[13] Robert Z, Tony S A, Bernardine D M, et al. Multi-robot exploration controlled by a market economy[C]∥Proc of the 2002 IEEE International Conference on Robotics adn Automation, 2002:3016-3023.

[14] Sheng Wei-hua, Yang Qing-yan, Tan Jin-dong, et al. Distributed multi-robot coordination in area exploration[J]. Robotics and Autonomous Systems, 2006, 54(12):945-955.

[15] Moravec H P, Elfes A. High resolution maps from wide angle sonar[C]∥Proc of the 1985 ASME International Computers in Engineering Conference and Exhibition, 1985:375-380.

附中文参考文献：

[2] 邹智荣, 蔡自兴, 陈白帆. 移动机器人SLAM中一种混合数据关联方法[J]. 小型微型计算机系统, 2011, 32(7):1340-1343.

[3] 房芳, 马旭东, 戴先中. 一种新的移动机器人Monte Carlo自主定位算法[J]. 东南大学学报, 2007, 37(1):40-44.

[4] 戴博, 肖晓明, 蔡自兴, 等. 一种基于激光雷达的移动机器人环境建模新方法[J]. 机床与液压, 2007, 35(1):14-18.

[5] 尚文, 马旭东, 戴先中. 融合多传感器信息的移动机器人自定位方法[J]. 东南大学学报, 2004, 34(6):784-788.

[6] 孙凤池, 黄亚楼, 康叶伟. 基于视觉的移动机器人同时定位与建图研究进展[J]. 控制理论与应用, 2010, 27(4):488-493.

[7] 张学习, 杨宜民. 基于全向视觉的移动机器人实时全局地图构建[J]. 计算机测量与控制, 2011, 19(3):643-646.

[8] 刘利枚, 蔡自兴. 多机器人地图融合方法研究[J]. 小型微型计算机系统, 2012, 33(9):1934-1937.

[9] 蔡自兴. 多移动机器人协同原理与技术[M]. 北京:国防工业出版社, 2011.

[10] 赵东, 郑时雄. 基于广义势场的多机器人避碰算法[J]. 华南理工大学学报, 2010, 38(1):124-127.

[11] 王硕, 谭民. 基于协商和意愿强度的多自主移动机器人避碰协作[J]. 高技术通讯, 2001, 11(10):70-73.

[12] 潘薇. 多移动机器人地图构建的方法研究[D]. 长沙:中南大学, 2009.