基于LM算法的棒束通道内空泡份额预测模型研究

周云龙 侯延栋 李洪伟 孙 斌

(东北电力大学能源与动力工程学院，吉林 吉林 132012)

核反应堆在“半环”运行期间发生小破口冷却剂丧失事故(SBLOCA)或余热排出系统损坏的情况下，堆芯内的冷却剂被衰变热加热，燃料棒束间冷却剂的池沸腾很有可能发生。在这种情况下，空泡份额的分布是决定两相混合程度的重要两相流参数。因此，准确地预测空泡份额对核反应堆设计和安全运行是至关重要的[1]。

目前，在一些文献中已经提出了一些预测棒束间空泡份额的预测模型。Cunningham J P和Yeh H C通过修改Wilson’s基于模拟压水堆发生失水事故而得出的经验关系式，提出了棒束通道的空泡份额预测关系式[2]。Ishizuka T等在高压条件下做了8×8棒束的实验研究，提出了漂移流模型的经验关系式[3]。Kamei A等对4×4棒束中空气和水的气液两相流进行了研究，得出了漂移流模型分布参数和漂移速度的经验关系式[4]。Paranjape S等基于8×8棒束的实验研究得出了漂移流模型的经验关系式[5]。但是，由于受到实验条件的限制，大多数模型的适用范围非常有限，仅限于实验的条件范围内，很难在实际中得到广泛应用。因此，能够提出一个可以在较大范围内预测空泡份额的模型是十分必要的。

由于人工神经网络具有良好的容错性和自适应性，许多人采用神经网络的方法解决非线性系统的建模问题，取得了满意的效果。基于此，提出了构建人工神经网络预测棒束通道内空泡份额的方法。笔者应用Anklam T M和Byong-Jo Y的实验数据成功训练出了人工神经网络(ANN)，并用训练成功的ANN提出了棒束通道内空泡份额的预测关系式。

1 ANN的构建和分析①

1.1 BP神经网络和LM算法简介

BP神经网络是一种多层前馈神经网络,包括输入层、隐含层和输出层，是利用非线性可微分函数进行权值训练的网络，其基本学习过程由信号的正向传播与误差的反向传播两个过程组成。预测值与真实值之间的误差从输出层经过隐含层逐层修正各连接权值,最后回到输入层，也叫误差逆传播算法，其结构如图1所示。标准BP算法存在一些不足，如易形成局部极小而得不到全局最优；训练次数多使得学习效率低，收敛速度慢。为了提高其性能，BP神经网络的改进主要有两种途径：一是采用启发式学习方法；二是采用更有效的优化算法。

图1 BP神经网络结构

LM(Levenberg-Marquardt)算法是梯度下降法和高斯-牛顿法的结合，既有高斯-牛顿算法的快速收敛特性又有梯度下降法的全局特性，网络训练通过不断地调整权值和阈值来实现，可以有效地改善网络的收敛性能。其基本思想是：为了减轻非最优点的奇异问题，使目标函数在接近最

优点时，极值点附近的特性近似二次性，以加快寻优收敛过程，同时在梯度下降法和高斯-牛顿法之间通过自适应调整来优化网络权值，这大大提高了网络的收敛速度和泛化能力[6]。其权值调整公式为:

ΔW=-(JTJ+μI)-1JTa

(1)

式中a——误差向量；

I——单位矩阵；

J——误差对权值微分的雅可比矩阵；

μ——标量。

当μ较大时，LM算法接近于具有较小学习速率的梯度下降法，当μ=0时,该算法成为高斯-牛顿法。

1.2 BP神经网络模型结构设计

笔者采用的实验数据取自于文献[7，8]的实验结果。实验装置分别为3×3和8×8棒束，实验工质为水，实验参数的范围见表1。

表1 实验参数范围

输入参数为：冷却剂的压力p、冷却剂的质量流速G、加热棒束的热流密度q、气相折算速度Jg、液相折算速度Jl、棒距与棒径之比p/d、测点轴向距离与当量直径之比Z/DH。输出参数为：空泡份额α。

利用选择好的输入参数和输出参数的误差反向传播ANN对实验数据的60%进行自适应训练，20%用于防止过拟合，剩余20%用于检测预测精度。

1.3 统计参数分析

为了更好地说明预测值与实验值之间的剩余误差，采用统计参数均方根误差(RMSE)来说明预测模型的精度。计算公式如下：

(2)

式中 Exp(i)——实验值；

n——数据个数；

Pre(i)——预测值。

2 ANN模型预测和结果分析

2.1 敏感性分析

通过敏感性分析可以评价输入变量对神经网络训练和学习的影响，找到对空泡份额预测影响很大的输入变量。根据人工神经网络训练过程中使用的权值，输入变量对空泡份额的相对重要性Im定义如下[9]：

(3)

式中i——输出层节点数；

IW——输入层与隐层之间的权值；

j——隐层节点数；

k——输入层的节点数；

LW——隐层与输出层之间的权值；

m——第m个输入变量。

根据输入变量对空泡份额的相对重要性计算公式，得到了归一化的输入变量对输出变量影响的敏感性分析结果(表2)。

表2 归一化的输入变量对输出变量影响的敏感性分析结果

从表2中可以看出,测点轴向距离与当量直径之比Z/DH、质量流密度G、加热棒束的热流密度q对空泡份额有很大的影响。因此，在对棒束通道内空泡份额的预测模型进行研究和棒束通道内的流型划分时，上述影响因素必须充分考虑，才能得出准确的经验关系式和流型图。

2.2 预测结果对比

图2为棒束通道内空泡份额的预测结果与实验结果的比较。从图中可以看出，当空泡份额α小于0.2时，约70%的数据落在了相对误差为±20%之间的区域内；当α大于0.2时，约95%的数据落在了相对误差为±25%之间的区域内。

此外，一些国外学者已经提出了许多预测空泡份额的模型，这些模型中应用最广泛、精度较高的属于漂移流模型，但是大多数都是根据大直径

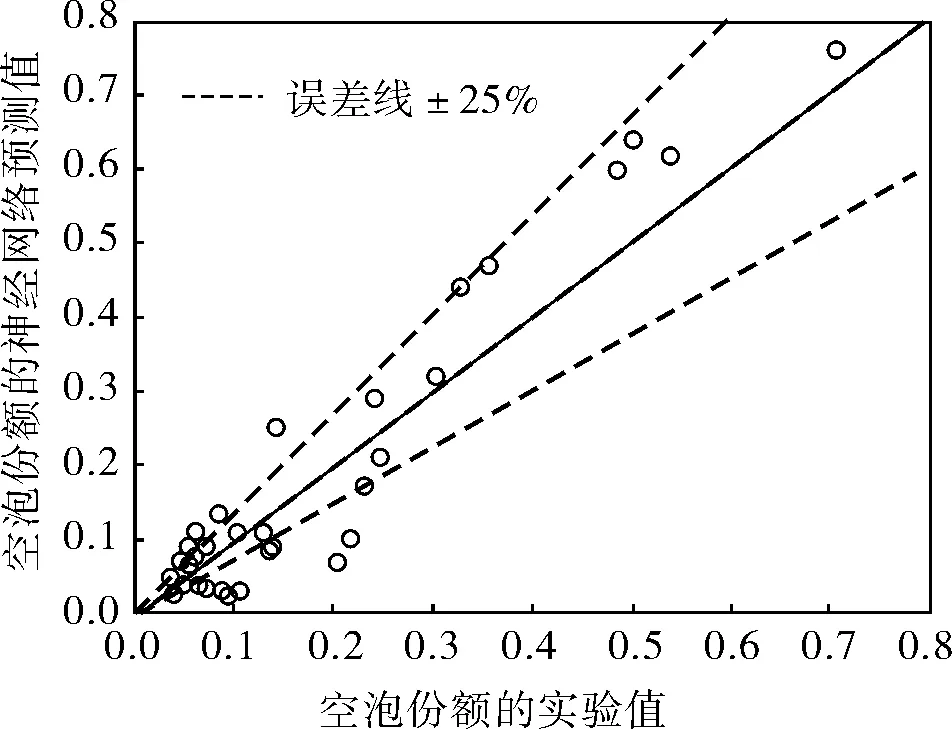
图2 神经网络预测结果和实验结果的对比

管道和环形管道提出来的，如果将这些模型直接应用于棒束通道，空泡份额的预测值将存在很大的误差。笔者将针对棒束通道提出的预测模型的关系式进行了整理，见表3[10]。

表3 棒束通道内空泡份额的预测模型

漂移流模型计算空泡份额的基本公式为:

(4)

式中C0——分布参数；

——面积平均的平均流速；

——面积平均的气相折算速度；

Vgj——漂移速度；

<α>——面积平均的空泡份额。

为了更好地说明神经网络预测的可行性和可靠性，笔者对表3中列出的Cunningham J P and Yeh H C模型、Kamei A模型、Paranjape S模型与神经网络进行的预测值进行了对比。图3为神经网络预测值和空泡份额预测模型预测值之间的对比。图3a表明Paranjape S模型的预测值偏低于实验值，而神经网络的预测值偏高于实验值，但神经网络的预测值在误差范围内，它的准确度高于Paranjape S模型。图3b表明当空泡份额值小于0.15时，神经网络的预测值接近实验值且在误差范围内，而Kamei A模型的预测值与实验值误差很大且在误差范围外；当空泡份额大于0.15时，神经网络的预测值和Kamei A模型的预测值都在误差范围内。图3c表明神经网络的预测值接近实验值，能较好地预测空泡份额，而Cunningham and Yeh H C的预测值严重偏离实验值，不能准确地预测实验值。综上所述，神经网络能较好地预测棒束通道内的空泡份额。

a. 空泡份额的实验值与神经网络预测值

b. 空泡份额的实验值与神经网络预测值

c. 空泡份额的实验值与神经网络预测值

2.3 空泡份额预测关系式

在人工神经网络训练和学习的过程中，对不同的隐层节点数和隐层-输出层的传递函数通过空泡份额期望值与目标值之间的均方根误差进行反复评价，最终得到输入层节点数为7、隐层节点数为8、输出层节点数为1、传递函数为tansig-linear的最佳网络结构(表4)。此外，根据在训练过程中得到的最优化的权值和偏差系数，得出了神经网络的空泡份额预测关系式：

(5)

式中b1、b2——偏差系数；

i——输出层节点数；

In——输入层的输入变量；

IW——输入层与隐层之间的权值；

j——隐层节点数；

k——输入层节点数；

LW——隐层与输出层之间的权值。

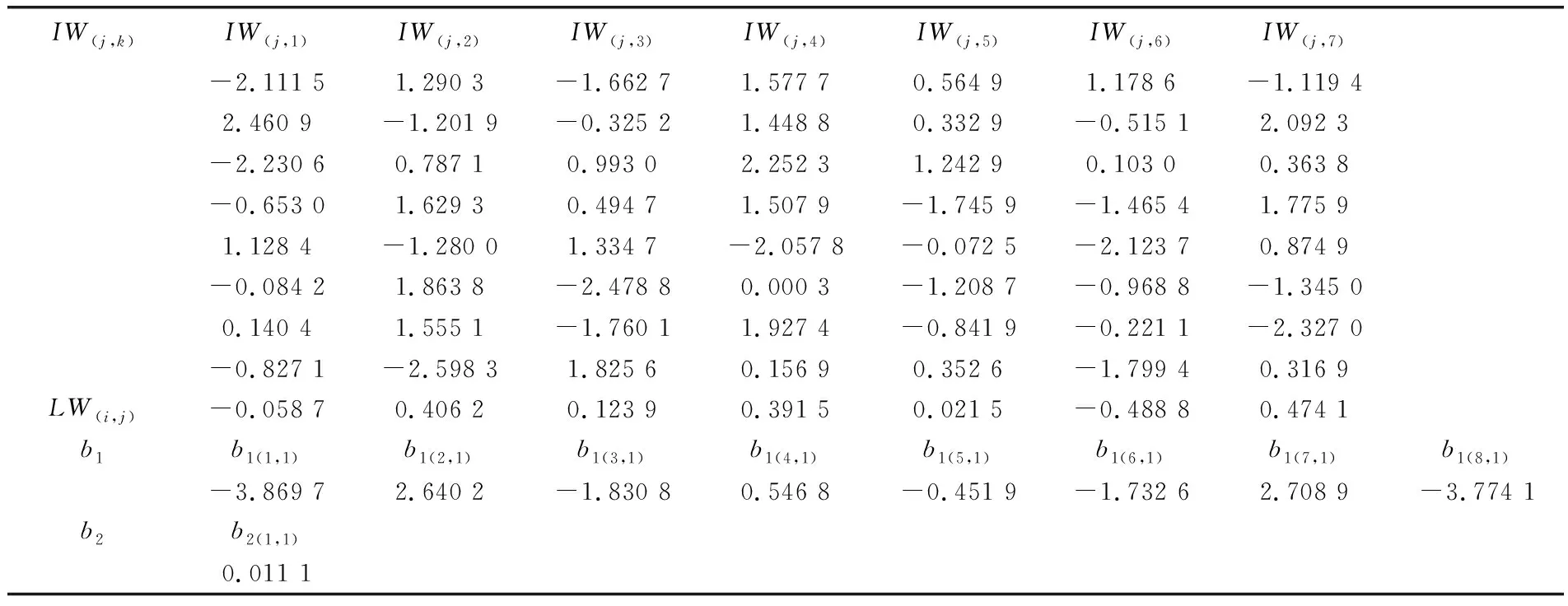
表4 神经网络模型的学习和测试过程中的优化权值和偏差系数

为了验证预测模型的精度，采用35组实验数据，根据均方根误差对表3中的3种预测模型和笔者提出的空泡份额预测关系式进行评价，结果见表5。

表5 不同预测模型的对比

通过以上数据可以看到，基于LM算法的棒束通道内空泡份额预测模型优于其他3个模型，其均方根误差为7.80%。所以，采用笔者开发的模型可以预测棒束通道内的空泡份额。

3 结论

3.1通过输入变量对输出变量影响的敏感性分析，发现测点轴向距离与当量直径之比Z/DH、质量流密度G、加热棒束的热流密度q对棒束内空泡份额有很大的影响。

3.2通过神经网络预测值与Cunningham J P and Yeh H C模型、Kamei A模型、Paranjape S模型预测值之间的对比发现，神经网络能在较广的参数范围内预测棒束通道内的空泡份额，为棒束内空泡份额的预测提供了一种简单可行的方法。笔者提出的空泡份额关系式预测值与实验值的均方根误差为7.80%，且ANN具有较强的容错能力和较好的鲁棒性，可以在宽广范围内准确地预测空泡份额，同时ANN还具有较强的参数敏感性分析能力。