基于峭度系数和隐马尔科夫模型的气液两相流流型识别方法
王艳霞 王迎迎 樊春玲
(青岛科技大学自动化与电子工程学院,山东 青岛 266042)
两相流动广泛存在于动力工程、化工工业、石油工业、工艺设备和其他相关领域[1],两相流流型的识别已成为重要的研究方向。由于两相流流动的复杂性,电导波动信号具有与电容信号相似的非平稳特性。经验模态分解(Empirical Mode Decomposition,EMD)是一种自适应时频分析方法,它可以有效地处理非线性、非平稳的信号[2],周云龙等用EMD分解压差波动信号得到IMF分量,提取IMF分量的能量,并将其作为特征向量对流型进行识别,取得了很好的效果[3]。
鉴于隐马尔可夫模型(Hidden Markov Model,HMM)近几年不断发展,并且成功应用于识别领域。周云龙等将小波包多尺度信息熵和HMM相结合,对采集到的电导波动信号进行小波包分解,并提取各频带信号的小波包多尺度信息熵特征作为流型的特征向量,将其输入到3种状态的HMM中进行训练并识别流型;将希尔伯特-黄变换作为特征向量输入到HMM对流型的识别,都取得了很好的识别效果,而且不同的特征向量对HMM的两相流的识别影响很大[4,5]。
针对所采集电导波动信号具有与电容信号相似的非平稳特性,笔者采用EMD方法实现对信号的线性和平稳化处理,在保留数据本身特性的同时,得到IMF分量并计算峭度系数。将计算得来的峭度系数作为特征向量输入到HMM中对两相流进行分类,从而实现了对泡状流、段塞流和混状流这3种典型流型的识别。
1 理论基础①
1.1 经验模态分解
经验模态分解是由Huang N E等于1998年提出的一种数据分析方法,适合于分析非线性、非平稳信号序列,具有很高的信噪比[6,7]。EMD能使复杂信号分解成有限个本质模态函数分量,所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号。其分解过程如下:
a. 对于原始信号x(t),首先确定其极大、极小值点,求出上包络线和下包络线的平均值m1,然后用原始信号x(t)减去m1,得到h1=x(t)-m1。
b. 检查h1是否满足IMF条件。如果不满足,将h1视为新的x(t)按照上步继续筛选,得到h2=h1-m2。重复筛选k次,得到hk=hk-1-mk,直到hk满足IMF条件,得到第一个IMF分量,记为c1=hk。
采用标准差SD的值判断筛选结果是否为IMF分量,SD的计算式为:
(1)
这里SD的取值为0.3。
记r=x(t)=c1,将r视为新的x(t),重复以上步骤,得到c1,c2,…,cn,直到r(t)成为单调函数或|r(t)|很小,无法再分解IMF时,整个EMD分解完成。原始信号x(t)可以表示成n个IMF分量与一个平均趋势分量的组合r(t)之和,即:
(2)
1.2 峭度系数
由于不同流型的IMF不同,采用峭度系数对IMF进行定量分析。随机变量x的峭度系数为:
(3)
若x服从正态分布,则k=3。流型不同,电导波信号的幅值分布接近正态分布的程度不同,从而引起峭度系数的变化。
对于采样频率一定的信号xi(i=1,2,…,N),其峭度系数k定义为:
(4)
对电导波动信号的各固有模式函数进行计算,这里取主要信息的前8个IMF分量,得到流型的特征向量T为:
T=[k1,k2,…,k8]
(5)
2 气液两相流电导波动信号的获取
垂直上升气液两相流动态实验是在天津大学三相流流动模拟装置[8]上进行的。图1为水流量为8m3/h时垂直上升管中气液两相流的电导波动信号,图中纵坐标为相含率电极测得的电压波动信号。实验中共观察到3种典型流型(泡状流、段塞流和混状流)的变化。

图1 3种流型的电导波动信号
3 电导波动信号处理与分析
对电导波动信号进行EMD分解,得到各尺度分量,IMF分量包含了原始分析信号不同频率下的特征信息。前7个IMF分量包含流型特性的主要信息,其余项不予考虑[9]。图2所示为段塞流和泡状流电导波动信号经EMD分解得到的IMF分量图。
对实验采集的3种流型的压差波动信号进行计算,得到3种流型的峭度系数如图3所示。从图3中可以看出泡状流的峭度系数分布接近正态分布,其变化范围较小。这是因为泡状流液相中存在小气泡,使它表现出低幅高频的特性。在段塞流和混状流中,出现了连续的气相和液相,所以在峭度系数中前面的为正值,后面的为负值,这与其特征相一致。而且段塞流的峭度系数相差最大,偏离正态分布最大。由于他们的峭度系数接近正态分布,所以压差波动信号的IMF峭度系数可以用作特征向量。

图2 段塞流、泡状流IMF分量图


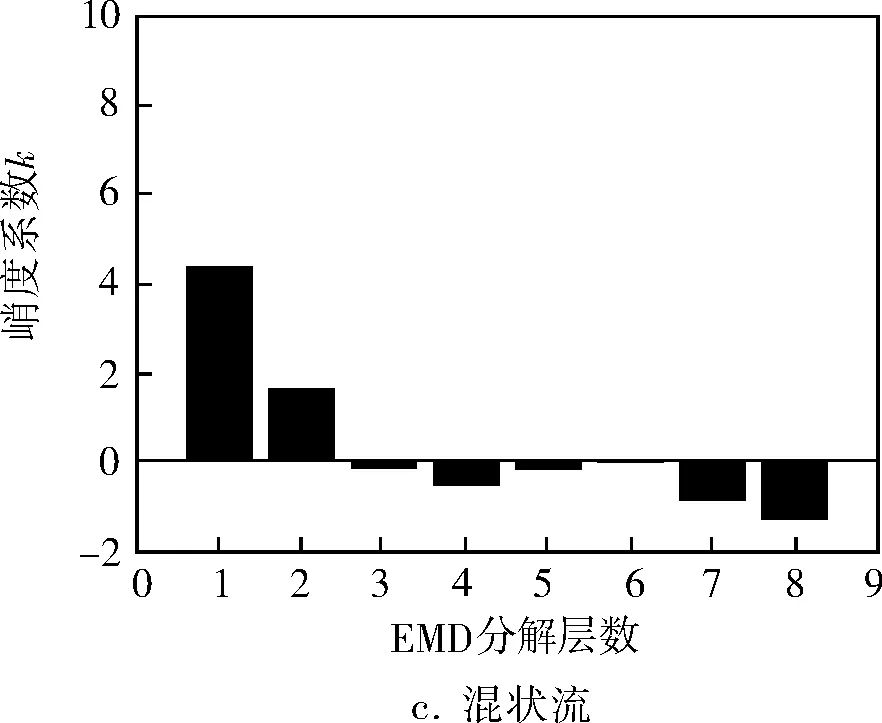
图3 3种流型固有模式函数的峭度系数
4 基于隐马尔科夫的流型识别
4.1 HMM的相关数学描述
隐马尔科夫模型是一个双重随机过程,一个HMM可以由以下5个参数来描述:状态数目N、观察序列M、初始概率矩阵π、状态转移概率矩阵A和观察值概率矩阵B[4]。
由于状态的3种概率分布都是不确定的,因此在建立HMM过程中,首先对系统模型进行训练,然后根据训练好的HMM进行状态识别。HMM具有基本的3种算法:Viterbi算法,前向-后向算法和Baum-Welch算法[4]。
4.2 HMM的参数设定
对采集的电导波动信号利用HMM进行流型的识别,根据所采集流型不同的特征来确定模型的状态,这样每一种流型特征代表一种状态。
为了识别这些流型,需要建立3个HMM。在对模型λ=(π,A,B)初始化时,由于π和A的初始值选取对训练结果影响不大,可设:
π=(1 0 0)

而B的初始值可以通过多变量高斯密度函数近似得到,即[9]:
(6)
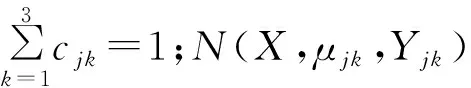
4.3 HMM的识别过程
对垂直上升管中两相流流型的HMM识别的全过程如图4所示。预处理是对采集的信号进行去噪,然后对信号提取特征向量。这些特征向量就是训练序列。在训练过程中,对3种流型建立相应的HMM,首先对HMM的初始参数进行设置,通过对样本的训练得到重新估计后的HMM参数,将所有的模型参数保存形成HMM参数库。在识别阶段,电导波动信号经过特征提取后,输入到每种流型的HMM中,经Viterbi算法分别计算出模型λ的参数匹配下P(O|λ)的输出概率,概率最大的HMM模型就是当前流型状态。
笔者选取120个样本集进行训练,即泡状流、段塞流和混状流各40例,得到3种流型中各自最优的HMM模型。在HMM训练中,选取最大的迭代步数为80,算法的收敛误差为0.001。3种模型的迭代步数与对数似然概率的关系如图5所示,每次训练的对数似然概率值见表1。
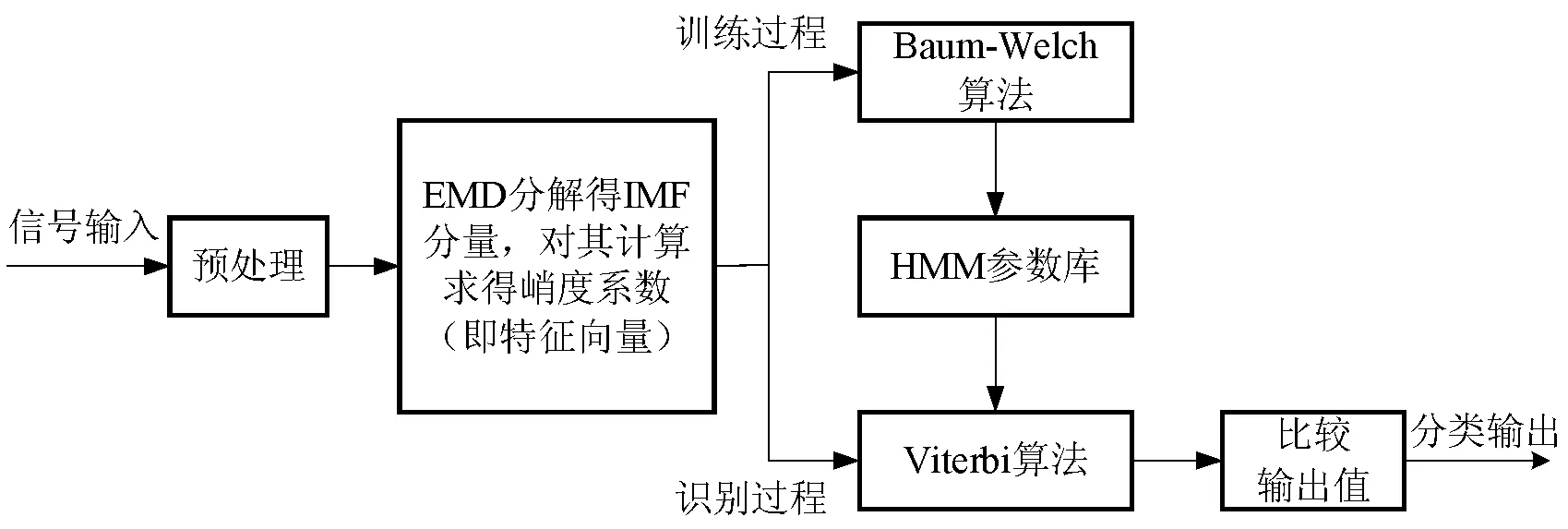
图4 基于HMM的流型模式分类系统

图5 3种流型的训练迭代步数
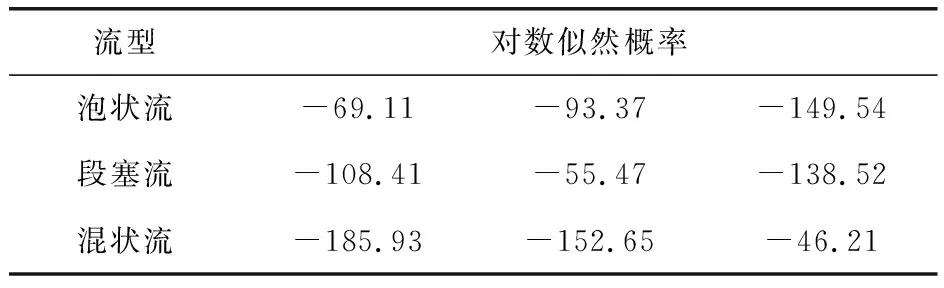
流型对数似然概率泡状流-69.11-93.37-149.54段塞流-108.41-55.47-138.52混状流-185.93-152.65-46.21
由图5和表1可知,该方法具有很好的收敛性质和很快的收敛速度,在15步左右就开始收敛,说明识别效果良好。将泡状流的数据输入到对应的HMM中,得到的模型对数似然概率为-69.11,与该模型的最大输出概率较为接近;把泡状流的数据输入到段塞流和混状流的HMM中,得到的模型对数似然概率分别是-93.37和-149.54,都小于泡状流HMM的最大对数似然概率,取得了较好的识别效果。
5 结束语
在解决非线性的信号处理问题上,经EMD分解后得到固有模态分量,再通过峭度系数的计算形成的流型的特征向量,然后输入到HMM进行识别,取得了较好的识别效果。在垂直上升管中气液两相流流型识别中,HMM识别方法在实际计算中得到了满意的识别效果,从而为流型识别提供了一种新的研究思路和方法。

