卡尔曼滤波器在储罐液位监控系统中的应用
王慧锋 吴中相
(华东理工大学信息科学与工程学院,上海 200237)
储罐液位监控是库区自动化中的重要一环,关系到库区的经济效益及运行安全等多方面问题。由于储罐的容量较大,单位时间储罐液位高度变化微小且微小的高度误差都会带来很大的容量误差,因此精确稳定的液位监测和高精度的液位控制显得异常重要。
储罐液位的自动测量仪表通常采用伺服液位计、超声波液位计及雷达液位计等。通过读取仪表的液位信号,完成对储罐液位的监控过程。但液位仪表检测出的储罐液位信号常常伴有以下问题,如储罐进出料、油轮上储罐或搅拌器运行时液面发生的波动及液位信号夹杂着测量噪声等,都会影响储罐液位的监控效果。解决此类问题的关键在于对储罐液位信号进行滤波处理,将影响液位监控的液面波动、测量噪声和失波效应滤除,从复杂的现场液位信号中获取真实平稳的液位信号从而实现高效的液位监控。传统的方法如平均值滤波等[1],会在一定程度上避免噪声对监控造成的影响,但当发生诸如液位信号夹杂能量较高的噪声、超声波或雷达液位计发生短暂虚假回波或储罐液位长时间周期性波动等情况时,其滤波效果不明显,且算法的实时性差,影响控制效果。文献[2]提出的误差回归模型方法,在特定条件下可以很好地预测真实液位,但该方法适应性较差,不同情况需要采用不同的误差模型完成对误差液位的修正处理,且该方法并没有从本质上滤除液位信号的干扰和噪声。
针对平均值滤波及噪声回归模型等方法的缺陷,结合实际应用背景并对各类滤波方法进行深入研究后[3~6],笔者提出了基于卡尔曼滤波器的储罐液位监控方法,并将其应用在COC储运培训中心的库区自动化控制系统中,实现了储罐液位的稳定监测和高精度控制,收到了理想的效果。
1 储罐液位动态模型分析①
储罐液位模型结构如图1所示。
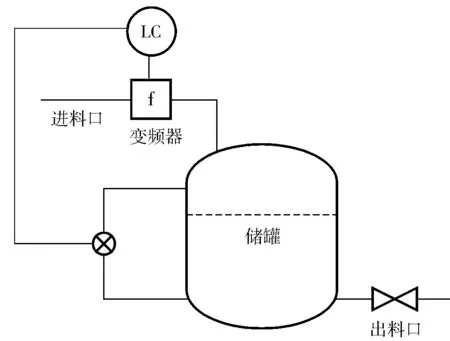
图1 储罐液位模型
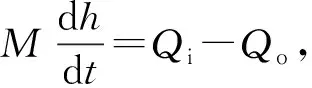
(1)
2 卡尔曼滤波器的状态估计原理
卡尔曼滤波的基本思想是采用信号与噪声的状态空间模型,利用前一时刻的估计值和现在时刻的观测值来更新对状态变量的估计,求出现在时刻的估计值。卡尔曼滤波在随机干扰和噪声的情况下,以线性最小方差估计方法给出状态的最优估计值[8~10]。
由于笔者讨论的是卡尔曼滤波在Rockwell PLC平台上的实现,属于离散系统的范畴,因此在滤波前,首先要将待滤波系统的传递函数离散化:
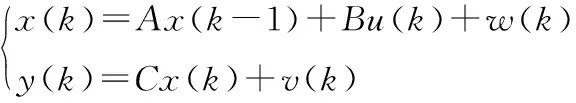
(2)
其中x(k)是k时刻的系统状态,u(k)是k时刻对系统的控制量,A和B分别是系统矩阵和控制矩阵,C为输出矩阵,w(k)和v(k)分别是k时刻的控制和测量噪声,且满足E[w(k)]=E[v(k)]=0,E[w(k)wT(j)]=0,E[v(k)vT(j)]=R,E[v(k)wT(j)]=0。
卡尔曼滤波器的滤波过程分为两部分,分别为时间更新环节和测量更新环节,时间更新环节预测测量更新环节所需要的参数,测量更新环节修正时间更新环节的测量结果。
时间更新环节包含两个方程:
x(k|k-1)=Ax(k-1|k-1)+Bu(k)
(3)
P(k|k-1)=AP(k-1|k-1)AT+BQBT
(4)
其中,x(k|k-1)为k时刻的先验状态估计值(根据系统过程原理或经验得到的估计值),x(k|k)为k时刻的后验状态估计值(结合之前的先验状态估计值和加权测量值得到理论上最接近真实值的结果)。定义系统的先验协方差和后验协方差分别为P(k|k-1)=E[e(k|k-1)·e(k|k-1)T]和P(k|k)=E[e(k|k)·e(k|k)T],其中e(k|k-1)=x(k)-x(k|k-1)为系统的先验误差,e(k|k)=x(k)-x(k|k)为系统的后验误差。
测量更新环节包含3个方程:
(5)
x(k|k)=x(k|k-1)+K(k)[Z(k)-Cx(k|k-1)]
(6)
P(k|k)=[I-K(k)C]P(k|k-1)
(7)
其中,K(k)为Kalman增益或混合因子,Z(k)-Cx(k|k-1)包含了所有的误差信息,称为新息。
卡尔曼的滤波过程为:
a. 根据式(3)计算当前时刻系统状态的先验估计值x(k|k-1);
b. 根据式(4)计算当前时刻系统协方差的先验估计值P(k|k-1),此时完成了时间更新环节,随后进入测量更新环节;
c. 根据式(5)计算Kalman增益K;
d. 根据式(6)计算当前时刻系统状态的后验估计值x(k|k),该值即本轮计算的状态输出值;
e. 根据式(7)更新当前时刻系统的后验协方差P(k|k)。
所有步骤结束后即完成了卡尔曼滤波器的一个工作周期。
3 基于卡尔曼滤波的储罐液位监控原理
3.1 储罐液位监测
储罐液位监测常伴有测量干扰,包括液位测量仪表本身的噪声及进出料时液位上表面的波动等。将卡尔曼滤波器配置在液位测量仪表的后端,可以很好地抑制测量干扰,且可设置不同的测量噪声协方差R实现对液位不同性能的跟踪。液位监测的原理如图2所示。
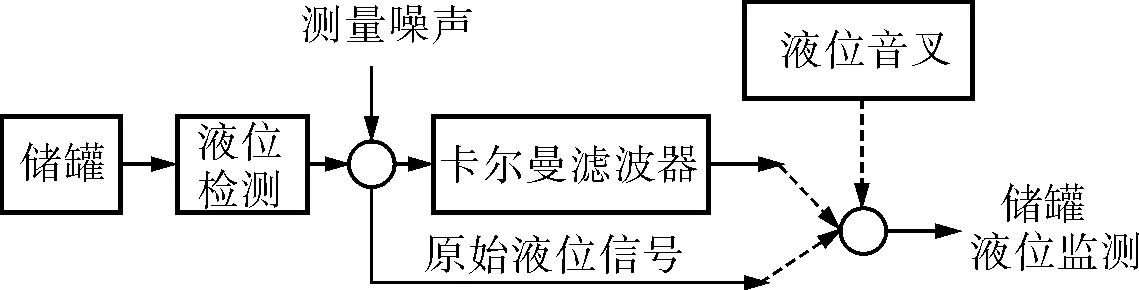
图2 储罐液位监测原理
监测模式下的卡尔曼滤波器的工作不依赖于系统的模型,且无控制变量参与系统状态的估计,而仅根据输入信号进行滤波。因此,液位监测时的卡尔曼滤波器参数应设置为A=1,B=0,C=1。液位的原始信号反映储罐液位的动态变化,滤波信号反映储罐液位的稳定状态和变化趋势,再将储罐上的音叉信号融合在一起将实现完整的储罐液位监测系统。在海上航行的油轮上的储罐,由于颠簸,储罐液位上表面周期性波动剧烈从而触及高位音叉,使监控系统的高位报警时断时续,影响储罐监控效果。而在监控系统中加入卡尔曼滤波器后,液位检测仪表检测到的周期性振荡信号将被滤除。此时,若高位音叉报警,但滤波后液位信号低于音叉高度时,则高位音叉报警无效;而当滤波后的液位信号高于高位音叉位置且音叉报警时,则高位音叉报警有效。
3.2 储罐液位控制
采用PID算法控制储罐的液位,卡尔曼滤波器在PID控制策略中可起到对系统状态的准确估计,滤除噪声的同时可缩短传统PID算法的调节时间,降低超调等[11,12]。此时,卡尔曼滤波需要根据被控对象的状态方程和PID控制器的控制量实现对系统状态的预估。
基于卡尔曼滤波器的储罐液位PID控制原理如图3所示。
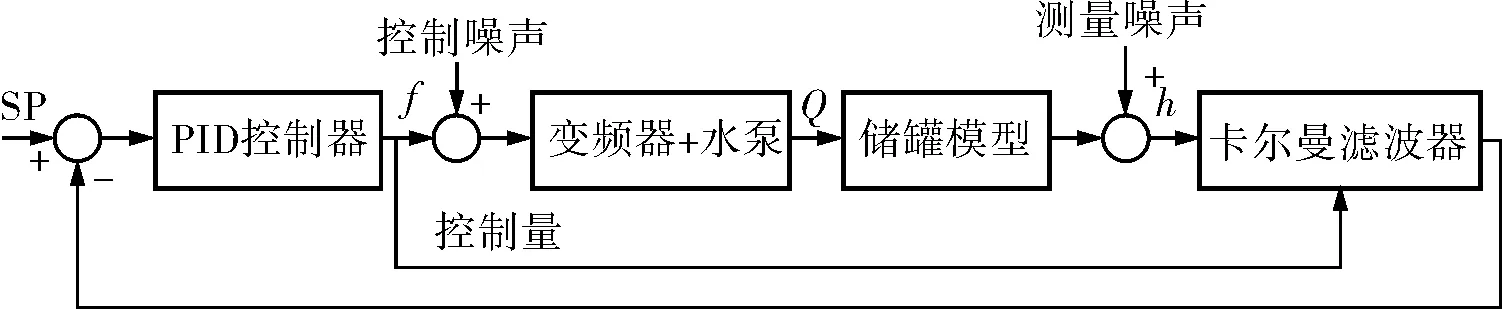
图3 储罐液位控制原理
将储罐液位模型离散化,求得A、B、C。将其代入卡尔曼滤波算法中,按照上述卡尔曼滤波步骤,完成对储罐液位的估计,随后求得与设定值的偏差,送入PID控制器计算控制量完成一次控制周期。
4 储罐监控系统的结构
储罐监控系统结构如图4所示,采用Rockwell Logix5000(1789-L62)控制器,现场选用的物位仪表为Endress+Hauser FMP51导播雷达,该雷达在量程小于或等于15m时精度可达±2mm,并以HART方式与控制器通信。变频器接入交换机与PLC通信,实现对水泵状态的读取和频率控制。上位机采用GE iFix SCADA系统。本测试库区包含1号和2号两个储罐,两储罐高度均为10m、截面积均为7m2,配合现场管路和离心泵可实现物料在两罐之间的输送,罐内物料为水。控制器的编程环境采用RSlogix5000 V20.00,编程语言采用 Structured Text(ST)。

图4 储罐监控系统结构
5 测试结果和分析
5.1 储罐液位监测
将变频器设置为50Hz输出,向一号罐上装料,同时向液位信号中加载强度为0.1的白噪声和频率为0.1Hz、幅值为2m的正弦波信号,极端方式模拟储罐装料过程,考察卡尔曼滤波获取储罐液位变化趋势的能力,测试结果如图5所示。可以看出,噪声液位信号已完全判断不出液位变化的趋势,与真实液位偏离较大。卡尔曼滤波器参数R分别设置为0.01、0.1和1时,3根曲线均很好地抑制了噪声信号,同时随着R值的增大,卡尔曼滤波器的输出与液位真实值贴合越紧密,表明R值越大的卡尔曼滤波器,其抗干扰能力也越强,而越小R值的卡尔曼滤波器,其输出跟踪输入的能力越强。在现场使用卡尔曼滤波器做储罐液位监测时,应根据现场噪声和监测要求合理改变R值。

图5 储罐液位监测测试
5.2 储罐液位控制

PID控制器参数设置为P=200,I=0,D=0,卡尔曼滤波器R=0.1。现将1号储罐内水排空,控制水泵进行装罐,液位设定点为1m,向储罐液位信号中加载强度为0.1的白噪声,幅值为0.1m。储罐液位变化情况如图6所示,由于白噪声作用,未加卡尔曼滤波器的储罐液位在设定值0.5m处不能收敛。而加卡尔曼滤波的液位输出平滑无波动,噪声对控制精度并未造成影响。PID控制器输出情况如图7所示,加卡尔曼滤波器后控制器输出平稳无波动,而未加卡尔曼滤波器的PID控制器输出则波动剧烈。向液位信号中加载频率为0.1Hz、幅值为0.1m的正弦信号时,控制1号储罐装料过程可得到相似的控制效果。
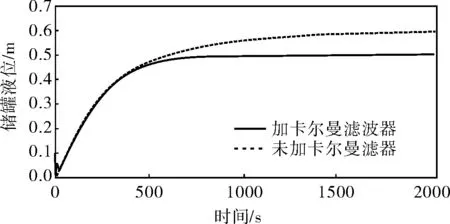
图6 储罐液位控制曲线

图7 PID控制器输出
由此可见,卡尔曼滤波器提高了PID控制器的抗干扰能力,很好地抑制了噪声及液面波动等对储罐液位监控造成的影响。同时,由于卡尔曼滤波给出了系统的最优状态估计,优化了PID控制器的调节作用,在对进出料同时进行的复杂储罐液位控制过程中,还将具备缩短调节时间及降低超调量等优点。
6 结束语
笔者提出了基于卡尔曼滤波器的储罐液位监控方法,该方法提高了储罐液位监测的稳定性和控制的精度。基于Rockwell PLC平台的卡尔曼滤波算法采用ST语言编制,并成功地将其应用在某公司COC储运培训中心的库区自动化控制系统中,收到了很好的液位监控效果。该方法及其在PLC平台上实现的方式,对库区储罐液位监控具有较高的指导意义和实用价值。

