算术基础中的哲学问题:古代与现代
B. C. 霍普金斯
(西雅图大学 哲学系, 美国 西雅图)
【哲学·科学技术哲学】
算术基础中的哲学问题:古代与现代
B. C. 霍普金斯
(西雅图大学 哲学系, 美国 西雅图)
与无时间的数学真理不同,导致数学真理产生的数这个概念是历史性的。古希腊数学明显将数区别于概念,相反现代数学则把数理解为一种具有概念特性的东西,或者说共有一种特性的概念的集合。无论哪一种数学概念,都面临两个基础性问题:在被数的意义上,事物的本性是什么?这些事物的数在何种意义上是统一性?毕达哥拉斯主义算术没有回答第一个问题,也就不能解释被同一个形式所统一的不同数之间的差异。柏拉图给出的答案是,设定具有差异化的一与多结构的相数。对相数的参与为每个数学数提供了使之区别于其他数的独特统一性。与古希腊数学完全不同,韦达“解析艺术”所开创的现代观念不再把数定义为多,而是多的概念。然而不同数的统一性何以各不相同这一难题仍然悬而未决。
柏拉图;韦达;算术基础;数;统一性;概念
一、绪言:数、历史与关于基础的哲学问题
本文的主题是关于古希腊与现代算术中的基础的哲学问题。出于多种原因,这一主题的本质尚不为当今哲学家、数学家及其学生所熟悉,所以一段解释性的绪言是有必要的。关于算术,在当今哲学家、数学家及受过教育的人们那里普遍存在着一个预设:数学真理不会变动,所以算术的真理是无时间的,即处于历史变迁之外。比如,5加7之和,曾经一直是且也将一直是12。现在基于这一完全合理的预设,人们也普遍引申出下面这个结论:导致数学真理产生的诸概念也是无时间的。所以对于算术,数这个概念被设定为先于任何其他概念,这些概念包含的意义是可确定历史时期的,因而仅在特定历史时期的背景下才有意义。关于概念对于历史性的意义的优先性的哲学术语是“先天的(a priori)”,其字面意思是“由先行者而来”,对于数而言就意味着,数的意义先于从而独立于由确定的历史时期或时代提供的意义背景。
然而第二个合理的预设——因为数学真理是无时间的所以数这个概念是先天的——却是错的,我今天正要证明这一点。古希腊算术所使用的是一个与现代算术使用的完全不同的数概念,这两个概念如此迥异,甚至应该说,古希腊数学家所理解的一个数之所与现代数学家所理解的数之所是截然不同的。首先,对于古希腊数学家来说,数明显区别于概念;然而对数的典型的现代定义将数理解为概念的特性,或者应该说是所有共有一个特性的概念的集合。这一差异是我今天的主题的一个重要的焦点,我会回到这一差异并探讨它的一些细节。这一差异被古希腊对数学的理解与现代对数学的理解——即他们对普遍意义上的数学与特殊意义上的算术的理解——的另一个基本差异强化了。在古希腊,μα′θημα(mathêma)就是能被学习与理解且一旦被学习就被认识的东西。所以,知识与古希腊对“数学”的理解密切相关,而且在此意义上的数学观念是所有希腊哲学与科学的范例。希腊算术作为学习的问题,首先关涉两个基本难题:在被数的意义上,事物的本性是什么;这些事物的数在何种意义上是统一体。我想我们都会同意,这些难题离今天我们关于计算的实践艺术的算术很远。这两个由古希腊算术提出的问题,当今是由数论来研究的。这就引入了我今天要说明的主题的第二点,即在关于基础的哲学难题中所涉及的问题。
在当代哲学的一个被其支持者与批评者称为“后现代”的分支里,“基础”是一个坏词,因为它被用来指这样一种原则或概念,它根据某个共同特性来解释复杂事物,排除了构成事物的多样化的一些重要方面,从而据说简化乃至篡改了复杂事物。譬如,笛卡尔就是典型的现代基础主义哲学家,因为他试图把知识建基于思想之中,而思想被认为是坏的,因为一旦思想被接受为一切知识的基础,人类的情感与感觉等其他能力——还是据说——(原则上)被否认能够产生知识。柏拉图则是典型的古代基础主义哲学家,因为他试图在一个由可模仿的形式(eidê)构成的智性领域中解释一切存在东西的基础,而这个智性领域被认为是坏的,因为一旦这种“彼岸世界的”形式被认为是一切实在的普遍支撑,那一切非智性的事物——最先且最重要的就是身体——都会遭到——还是据说的——不可避免的贬低,这里指的是对其生动性的价值的贬低。然而对于那些被古希腊人称为“数学家”的人及他们的哲学家,还有直到20世纪中叶为止的现代数学家来说,“基础”不是一个坏词。相反,这是一个好词,因为它指示在人类科学声称认识的真理背后的最高的从而也是最深奥的理由。没有这些理由提供的基础,数学家与哲学家一样都会将数学这种人类知识判定为不完整的,从而是不完美的。
在这种情况下,对于数学科学声称从而假装知道的东西的真相,必须有更深刻的理由。这一点由于被算术基本概念中的推理所发现的悖论与彻底的矛盾而被认为是明证的。对古希腊算术而言,数既表示众物又表示众物作为确定数目的统一性,这一事实被认为依据于一个深刻的矛盾:即同一个东西——数——既是多又是一,从而在其存在中联合了被人类语言永远认作不可联合的对立面的不同性质*正如以下引文所显示的,Kurt Gödel同样认识到古希腊人在算术的核心中发现的矛盾:集合是被其元素构成的统一体。将多纳入统一之中是心灵的一个基本特性。集合是多,也是统一体。多是统一体的对立面。集合实存看似一个矛盾的事实。然而令人惊讶的是,多也是统一体这一事实并没有导致矛盾:这个是数学的主要事实。一起思考[诸多东西]看似平凡无奇,这也似乎解释了我们为何没有矛盾。然而“众物为一”远非寻常[2]254。。对于现代数论而言,数的领域在“普遍分析”或“普遍算术”中从自然数向无理数、负数与虚数等的扩展,引发了难题,即如何将这些非自然数理解为数,即理解为回答“多少?”这一问题的计量单元或数目单元。
二、毕达哥拉斯主义算术中的基础的问题

已经提及的这两点——即被数之物的本性问题与它们的数在何种意义上是统一体问题——为希腊算术所涉及,毕达哥拉斯主义者关注第二个。被自己的数所表示的被数之物在任何情况下都是若干事物,与此同时它们的多又凭借自己的数而被理解为构成一组事物,或用今天的说法,事物的“一个集合”。为什么若干事物被把握为一负责这一关于基础的问题,正是毕达哥拉斯主义者的算术试图解决的问题。他们对这一问题的解决是通过按照数的εïδη(形式或类)——如奇数与偶数、正方形、立方形——来区分数,以援引被毕达哥拉斯主义者发现的、直到今天还被保留为算术术语的一些形式。与被数的确定量所规定的诸物不同,数的形式是自在为一的:所以奇数的形式只有一个,偶数的形式亦然,虽然奇数与偶数有无穷多个。除了这些熟悉的数的形式,毕达哥拉斯主义者还通过几何形式来区分数。几何形式在每一个被数的东西都被一个石子或圆点代表时是可见的。开始是一个这样的代表,然后许多组圆点再加上去,就产生了类似下面几种图形:三角形、正方形、五角形等。因这类图形而成形的数就按这些图形的名字来称呼,如三角形数、正方形数、五角形数等,所以这些图形被理解为那些石子或圆点被把握为“一“的原因。六个东西能被设想为“一”组,即设想为“六”,是因为三角形形式使6个东西成为一个。那么,10个东西也可以被设想为“一”组,即“十”,因为同样的三角形形式使它们成为一个。
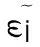
毕达哥拉斯主义者将数的各种形式或类理解为它们的“自然”秩序,而且他们把所有事物,尤其是可见物都理解为数,而数的本性就是为其统一性负责的确定的形式。所以,毕达哥拉斯主义“算术”不仅是我们所说的“数学”原则,而且是一门关于可见宇宙的科学,一门宇宙学,即关于我们宇宙的统一与秩序的科学。毕达哥拉斯主义者将他们的宇宙学算术扩展到通过将可听见的东西和声音与比率、比例及它们的形式和性质联系在一起,来研究数的形式与数本身之间的关系;从中就产生了古希腊人所谓的“逻辑学(logistic)”,即关于比率与性质的科学。这门科学将事物的数带入彼此之间的关系,且在古代与中世纪的代数发明之前,一直是所有计算的基础。
三、柏拉图解决算术基础之问题的尝试
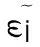
关于将数理解为特定事物的特定量所引起的第一个问题,柏拉图研究被我们用来数星星、牲口、士兵、德行等的数本身确切地是什么。当我们数“四”颗星、“四”头牲口、“四”个士兵、“四”种德行时,柏拉图主张,这个“四”明显不限于星星、牲口、士兵与德行,也就是说,“四”个确定的东西既非星星、牲口、士兵与德行,也非任何其他被我们的五官所把握的限定之物。所以对柏拉图而言,我们计数的能力必须预设,我们用来计数的数不是指这些具有感性特质的限定之物,而是指只能被我们的理智所设想的东西。也就是说,我们可以计数任何东西的任何数——在这里就是“四”颗星、“四”头牲口、“四”个士兵与“四”种德行,因为另一种由其性质不为我们感官所见因而是智性的事物之多构成的数,在我们开始计数这些具有可感性质的事物之多之前,就已经可被我们的理智所用。构成智性之数的事物之多具有如下性质:不变性,因为不像具有可感性质的事物,智性之物永远保持同一;完全等同,因为在只能被我们的理智所设想的多中的每个智性之物都不过是一;不可分性,因为绝对为一的东西不可被分割,分割了就多于一了。总之,只有“纯粹”单元之多的确定量,即“纯粹数”在人的心灵开始计数它要数的任何东西之前就能被心灵所用,人的计数能力才是可能的。所以据柏拉图来看,算术的毕达哥拉斯主义基础——数的形式——必须把纯粹单元之多作为其基础,这些单元构成了被计数活动所预设的纯粹数的源头。
柏拉图对毕达哥拉斯主义算术的“纯化”提供了一种算术,对于由这种算术所计数之物的本性的一种新视角,相应地导向了对于毕达哥拉斯主义者对众物如何能构成一个数这一问题的回答的批评。现在要考虑的是“纯粹”单元,所以这个问题要重新表述为:诸纯粹单元如何构成一个数?我们知道,尽管毕达哥拉斯主义者的数的形式具有将构成每个数的许多感性的“一”统一起来的功能,但它们迥异于数本身。这是因为这些单一的、即作为一的形式缺少与数的存在不可分离的多。所以这些形式不能解释被同一个形式所统一的不同数之间的差异。譬如我们知道,在毕达哥拉斯主义算术中,数“六”与数“十”各自是6个东西与10个东西的统一体,这是因为当这些东西被圆点代表时,它们具有三角形形式。然而对于柏拉图而言,无论这个形式还是偶数形式,都不能解释6个纯粹单元之统一体的形式与10个纯粹单元之统一体的形式之间的差异之本性。这是因为“统一”与“多”这些算术形式(或算术概念)不能说明由不同数所表达的多的统一中的诸差异;“六”与“十”都是纯粹单元之多的统一体,但它们作为数值统一体的本性是不同的,因为“六”比“十”小,也正因此,在数的自然序列中“六”先于“十”。据柏拉图看来,因为算术概念不能说明数之间的真正差异,所以算术不能充分解释自身。就是说,算术概念不能解释其作为科学的基础,因为这些概念不能解释其最基本的元素:数。
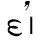

这种关于柏拉图对型相的理解的错误观点,在他最出色的学生亚里士多德批评柏拉图哲学时的肤浅理解中,在对他(亚里士多德)自己的关于形式的哲学的陈述中有其渊源。尽管柏拉图的对话确实把感性之物与其型相之间的关系说成前者对后者的“参与”,但是柏拉图的任何作品中都没有说,形式被设定为独立于或分离于感性世界中的事物而实存,或后面这种感性之物被描述为彼此分离,从而是“单数的”或“特别的”。相反,与柏拉图对型相的说明不可分离的是说明事物之多的统一性问题,无论这些东西可被感官感知,如一群蜜蜂的统一性,或只在思想中被理解,如善良行动的统一性。这就是说,我们已经看到的这个问题,处于柏拉图对将相数设定为算术最基本元素——数——的基础所需要说明的根底,也处于他对型相之说明中的参与问题的根底。所以,柏拉图对相数的说明不仅是他对算术基础的问题的解答,而且还决定着解决参与这个大难题的关键。

共同之物不描述必然共有它们的东西这类例外情况引发了一个问题:这一共同性质何在?“二”是某种分离于从而可以说“伴随”或“外在于”单个事物的东西吗(必须注意,当问“二”在哪里时,我们不是问“2”这个数学符号在哪里,毕竟这个符号自身是毫无意义的)?当柏拉图的对话《智者篇》的两个谈话者,一个来自爱利亚城的无名的陌生哲学家与一个叫做泰阿泰德的数学家发现一个被两个东西分享却不能被单独具有的共性这种典型情况时,谈话展示了解决这一问题的关键。
哲学家与数学家两个人的研究,即柏拉图所谓的“辩证法的”研究,指示了解决构成数的共性究竟何在这个问题的方法。这一指示发生在他们计数存在的部分(parts of Being)的努力失败时。他们失败,是因为存在的部分不像算术数的部分即“纯”(智性)一之多,而我们知道,就是这种多构成了算术科学所预设的数学意义上的“纯”数。这一失败在他们对哲学家所谓的“最大的类”,即运动、静止与存在的讨论中很明显。存在无非被规定为运动与静止,这就有问题了:这些形式的数是二还是三?所以,为对“存在是什么”这个哲学最基本问题之一的回答给予说明,被证明是要取得数这个算术的最基本元素的帮助的。
数学数并未证明能够胜任计算存在及其部分的任务,因为当静止被数作一,运动为另一个一,存在为第三个一时,他们的数加起来就是三。存在被数作“外在于”静止与运动的另一个形式,这是完全不可能的。之所以如此,是因为任何存在者必须不是静止就是运动的,所以必须具有静止与运动的性质,静止与运动不是三个东西而恰恰是“二”——虽然它们之为“二”的方式不像数学数中的两个东西之为二的方式。由上可见,作为算术之基础的数以相同的一为其部分。存在、静止与运动的形式的部分不仅不是相同的,而且是完全相反的——即使它们仍然是统一体,因为所有静止或运动的东西都分别被它们的性质所确认。虽然如此,但这仍是柏拉图的重要发现:正如存在形式不是某种“外在于”静止与运动形式的第三者而恰是这些形式之总和,同样,譬如二这个数并非某种“外在于”被它统一为“二”的单元的第三者,而恰恰是二个单元的总和。对于一个数学数或存在形式分别统一作为它们之部分的单元或形式的方式,柏拉图用的术语是“共同体”(κοινωνíα)。
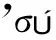
四、亚里士多德对柏拉图的算术基础之解答的批评及他自己的解答
根据亚里士多德的报告,柏拉图曾教导:有九个相数,双是第一个相数而十是最后一个,因为上文已说过,一在古希腊算术中不是一个数。而且我们还知道,亚里士多德的报告包含在他对柏拉图对算术基础问题的哲学解答的批评之中。亚里士多德的批评有三个焦点,它们在人类思想史上都发挥了巨大的影响。
第一个焦点关涉柏拉图对“参与”的说明。从通常的但却错误的观点看来,亚里士多德并未完全拒绝柏拉图事物参与形式的观点,只不过拒绝了柏拉图形式“分离(χωρισμ)”于事物的断言。所以对亚里士多德而言,没有形式的“以一统多(ενε′πí πολλν)”(《形而上学》,991a 2)的统一体。对双这个形式而言就意味着,“双数”是智性的“二”与分有它的事物所共有的。亚里士多德指责柏拉图将参与关系描述为复制世界,因为通过用“映像”和“模仿”等隐喻语言柏拉图引入了一种二元性——对于刚才提到的那种情况就是,“二”物之“双数”与作为“二自身”的双之“双数”——在此,只有双数的是双与任何两个东西共有的。
亚里士多德对柏拉图的批评的第二个焦点与第一点相关,因为亚氏否认在事物的数中有任何统一性。在我们结束计数时所说的那个词是表示若干事物,因而其自身根本不是一。被数的单元之多的“共同体”并不意味着它们的数自身是统一体。唯一与数相联系的统一体就是在计数过程中被重复的单元的统一体,如在一个苹果、一个苹果这样的数苹果过程中,两个苹果与六个苹果的统一体就是“苹果”。

不管柏拉图对基于相数的算术这门数学科学的哲学基础的说明有何问题,很显然的是,亚里士多德没有看到柏拉图试图解决的问题,即不同数之间的真正差异的问题。正如毕达哥拉斯主义者对数所共有的形式的诉诸不能说明被同一个形式所统一的不同数之间的差异,亚里士多德的唯一与数联合的统一性是计数中被用到的单元的统一性这一断言,同样不能对具有相同统一性的不同数作出说明。也就是说,正如毕达哥拉斯主义者基于六与十对相同的图形三角形的分享作出的对这两个数的统一性的说明,不能处理“六”与“十”这两个统一体之间的具体差异,亚里士多德基于两个苹果与六个苹果的共同单元“苹果”作出的对二者的统一性的说明,同样不能处理这两个数的具体差异。
五、现代算术之基础中的哲学问题
现在把讨论转到现代算术中的算术基础的问题,自始就必须确定的是,对算术基本元素——数——的现代理解与弗朗索瓦·韦达(François Viète)1591年为梅露辛公主(帕尔特纳的凯瑟琳,1554—1631)发明“解析艺术(Artem Analyticen)”*Francisci Vietae, In Artem Analyticem (sic) Isagoge, Seorsim excussa ab opere restituate MathematicaeAnalyseo, seu, Algebra Nova (Introduction to the Analytical Art, 作为一个独立的片段被从复原的数学分析作品即《新代数[Tours, 1591]》中摘出). English trans. J. Winfree Smith, Introduction to the Analytic Art, appendix to Jacob Klein, Greek Mathematical Thought and the Origin of Algebra, trans. Eva Brann (Cambridge, MA: The M.I.T Press, 1968). 编者引用时称作“Analtyic Art”。这一历史起源分不开。直到今天,这一“艺术”仍然作为形式化的必要条件起作用,而正是形式化使现代数学得以可能,从而可以说构成了它的基础。
韦达将他的解析艺术介绍为“新代数”并从“分析”这一古代数学方法得名,认为“分析”方法最先由柏拉图发现,所以称它为士麦那*古希腊城市,由伊奥利亚人建立。的讽刺诗(Theon of Smyrna)。古代的分析是几何学中用以发现未知的一种方法的“普遍的”一半,另一半“综合”在特征上是“特殊的”。这种方法在讽刺诗中被如此定义:分析是“把要探求的东西当作理所当然的并借助无可争议的真理的结果推进”,相反,综合则是“接受理所当然的东西并借助要探求的结论与理解的结果来推进”(Analytic Art, 320)。从分析向综合的过渡被称为“换位”,并且根据对几何定理或某个几何问题的答案(“解释”)是否在被证实(πδειξι),分析被分别称为“定理的”或“问题的”。
韦达的新发明涉及将算术分析的一种新奇形式——这种形式的分析见于最近重现的一个公元3世纪的亚历山大里亚的迪奥番图(Diophantus of Alexandria)的文本(标题就是简单的“算术”)——理解为与几何学分析完全平行的方法。这使韦达能够把要探求的未知数——被理解为单元之多的统一体——当作在其类别上已经被假定了的数。就数的类别而言,他继承了迪奥番图在《算术》中用的名称,即平方、立方、立方的平方与立方的立方。对每个未知的、不确定的数目的类别及每个已知的数目的类别,他都指定了一个来自字母表的他所谓“永恒的、明白的符号”(元音对应已知数,辅音对应未知数)。这不仅使单元的确定数目(即前现代因而非形式化意义上的数)能够按照好像确实已经给定的方式得到理解,而且使已知数按照它们的类来表达。韦达摒弃了对于分析的几何学方法的第二部分——即证明特殊定理或解决特殊问题的综合的定理的或问题的换位——相似的算术需求,从而使解决算术问题的“解析”——即不确定的因而“普遍的”——方法第一次成为可能。韦达的发明有三种重要的结果:1、在定理中与在问题中被代表的客体的类别的几何学区分消失了,由此在解析艺术中,定理与问题等同,“定理的”综合与“问题的”综合的区分也消失了;2、韦达的解析艺术使已知数与未知数两个种类之间的专门运算得以可能,他将这种被他称为“美的逻辑(logistice speciosa)”的运算应用于“纯粹”代数,也就是一般性地应用于发现未知数与未知的几何量级(由数所衡量);3、因为美的逻辑对它的计算——韦达所谓的“数的逻辑”——的方法的确切结果不感兴趣,所以韦达的解析艺术这一巧妙方法被构想为一个一般的辅助方法,其目的不是单个地解决问题,而是解决解决问题的一般能力的问题。被韦达刻画为“发现的艺术或发现发现的艺术”的普遍解析是数学领域中的一门工具,其意义正如亚里士多德的《前分析与后分析》是所有可能的知识领域的工具论一样。就这一点而言,韦达《解析艺术》的结论告诉我们:“解析艺术……通过扭转所有问题中的最高问题与自身相称,这个问题就是:不遗留任何未决的问题。”(Analytic Art, 353)
韦达的方法在数学史家看来是与数学公式和第一个现代公理系统的发明相一致的,通过公式与公理系统,数学分析的语法规则得以“定义”它们所应用于的对象。然而韦达的方法也与数学史家与哲学家至今不知的一种东西相一致:对算术基本概念——数——的存在方式的改造、对普遍意义上的数学对象的存在方式的改造以及对产生形式概念——它作用于普遍意义上的知识系统——的抽象过程的改造。
韦达的新观念包含三个相互关联、相互依赖的方面:1、其方法上的新观念使已知数与未知的、不确定的(所以是“一般性的”)数的计算成为可能;2、其认识上的新观念解决了在这一普遍状况下的数学难题,以至其不确定的答案容许任意多基于随意设定的数的确定答案;3、其解析的新观念可一般性地应用于传统算术的数与传统几何学的量级。
这一新观念的哲学意义在于数及其概念的形式化,由此数不再像我们前面看到的在希腊算术及先于韦达新观念的一般意义上的数学中那样,指示一个“由单元构成的多”(Euclid, Book VII, def. 2),而是指示就已知数而言的多的概念以及就未知数而言的这种(或一般意义上的)多的概念。数及其概念的形式化,既不能被亚里士多德的抽象也不能被柏拉图的辩证法所把握。这是因为形式化的数既非亚里士多德意义上的、产生衡量事物之多的单元的抽象的产物,也非柏拉图意义上的多的型相统一体,一旦数学家的感性假设被抛弃,这种统一体就被辩证法理解为不可还原到它所统一的事物上去。而对于韦达而言,数是从心灵与事物之多的直接联系攀升到心灵与它对这种直接联系的理解的关系这一概念过程的结果,同时他又把这两种关系模式看做一样。与具体事物之多的实在关系和与这个多的概念的认知关系,这两种异质的关系的同一,是由韦达同时赋予普通的数字符号与他的代数字母的意义显示的。对于他就像对于我们一样被展示从而明白的是,感官可见的字母每次都被直观为——不单单是指示——被谈论的一般概念——无论这个概念是这个还是那个数字,比如任何“二”的一般概念或任何“数”的一般概念。在这个对感性记号与一般概念的同时直观中,很明显的恰恰是韦达关于数学符号的新观念。
由韦达方法的解析的新观念得出的基础问题涉及语法规则的由来,而语法规则支配着公理系统并建立规定它们所应用于的不确定对象的系统语境。韦达对这些规则的建立是基于“数的逻辑”,所以也是基于以确定数量的单子进行的计算,即基于以古希腊算术所处理的“自然的”从而是非符号的数进行的计算。正是由此,没有数值特性的字母符号才得以在美的逻辑和以这种符号为基础的新代数中仍然具有数的意义。然而,韦达也从符号表象的角度对这些由单元构成的多进行概念化。这导致的一个重要结果就是,数与其一般的概念在数学与数学哲学中处于一种模棱两可的状态,即在其作为“一般数”的不确定的、一般符号的意义与其作为由单元构成的多的前形式化的自然意义之间摇摆。这种两可性或许在康德批判哲学的图式论中最显著,在那里图式被理解为“想象力为概念提供它的图像的一般程序”(A140/B179/180),而“数”为图式提供了第一个例证。所以对康德而言,在想“一个可以是五也可以是一百的一般数”时,数的经验图像,如一个排列中的点——对于五这个数而言就是五个(……)——区别于数的图式。我们无法找到一个比康德的如下断言更好的对这里所探讨的数的两可性的表达了,他声称“关于[一般数]的思想比图像本身更能反映一种对于某个概念相符的图像中的多(如一千)的表现方法”。康德对诉诸一个密集量级的例子来刻画作为范例的精确数量的先验存在方式这一做法的讽刺不能被形式化,遑论量化,不过这仍然是非常真实且深刻的。
当哥特洛布·弗雷格试图解决数的两可性通过在算术中彻底废除非形式化的数而对韦达的解析方法造成的难题时,解析方法的基础性新观念中的数及其概念的两可性的第二个重要结果就出现了。由此数与数的概念就统一起来了,因为数本身现在被定义为关于概念的断言,或更准确地说,它根据某种概念关系的结构——根据“语法”规定——而被定义。然而弗雷格的数根(numbercide)引起的难题是,两个集合——在他看来这是定义数的基础,他称之为“等势(equinumerosity)”——的元素之间一一对应的一致性如何说明数之间的差异?
将数定义为概念的谓词的“数值的”特性,如作为我们太阳系的行星的概念的数“九”,被理解为被例示“九”次这种特性。然而在不同集合的元素之间不同的一一对应的一致性中,是什么构成了不同数之间的差异?或者说,在等势这一概念性质中,如六与十的数值特性就是正好拥有六或十个“归入”相应概念下的事项这种定量特性,那么是什么规定了六与十的数值特性的差异?对于这种问题,数的概念定义无从解答。这是因为定义等势的一一对应的映射预设了而非创建了,以上面的例子来说,正好被例示六次或十次这种特性。那个柏拉图认为算术借助自己的术语无法解决的难题,即如何说明算术的基本假定——不同数的统一性确实各不相同——的难题仍然悬而未决。
(本文系作者于南京大学2013年“现象学精品课程”中的讲座稿,南京大学哲学系博士研究生谢利民译校。)
[1] Francisci Vietae.Introduction to the Analytic Art[M].English trans.J.Winfree Smith,appendix to Jacob Klein.Greek Mathematical Thought and the Origin of Algebra.trans.Eva Brann,Cambridge MA:The M.I.T Press,1968.
[2] Hao Wang.A Logical Journey.From Gödel to Philosophy[M].Cambridge MA:MIT Press,1996.
责任编辑:王荣江
O1-0
A
1007-8444(2014)06-0718-08
2014-05-20
伯特·霍普金斯(Burt Hopkins),教授,哲学系主任,当代英语世界著名现象学研究专家,主要从事20世纪欧洲哲学(特别是胡塞尔、海德格尔、克莱恩)、现代早期哲学、柏拉图哲学以及深度心理学研究。

