基于云模型的独立变桨距控制仿真研究

岳有军 徐 玥 赵 辉，2 王红君

(1.天津市复杂系统控制理论及应用重点实验室，天津300384；2.天津农学院，天津300384)

独立变桨距控制是在统一变桨距的基础上发展起来的一种新型控制方法，根据3个桨叶各自的受力情况单独进行调整，达到更好的控制效果。由于风切效应、塔影效应对风电机组的影响，风轮平面内风速的分布不均匀，因此在统一变桨距控制的基础上设计基于桨叶方位角权系数的独立变桨距控制系统。

在变桨距控制器的设计中，根据文献[1～3]，模糊PID控制效果较好。风电机组有强非线性、时变不确定性的特点，而不确定现象和事物具有模糊性和随机性。模糊PID控制是模糊控制与PID控制的结合，模糊控制需要用确定精确的隶属度函数描述模糊集，使模糊的概念变得精确，在推理过程中失去模糊性，从而归入精确数学理论中。但模糊控制只考虑了其模糊性，未能考虑风速变化导致的随机误差，因此用精确的函数来描述隶属度函数是不客观的。由于既要着重模糊性，也要考虑随机性，因此笔者提出基于云模型的控制方法。

1 独立变桨距控制系统①

1.1 风能利用系数

根据空气动力学原理，风能利用系数会限制风电机组的实际功率，其计算式为：

(1)

式中CP——风能利用系数；

S——风轮旋转一周所扫过的面积，m2；

ν——风速，m/s；

ρ——空气密度，kg/m3。

根据风机叶片的空气特性，风能利用系数是叶尖速比λ和桨距角β的函数[4]，CP=CP(λ，β)，即：

0.0018(λ-3)β

(2)

(3)

式中n——风轮转速，rad/s；

R——风轮半径，m；

ωr——风轮转动角速度，rad/s。

通过软件Matlab/Simulink可得到如图1所示的风力机风能利用系数CP(λ，β)的函数曲线。风速在额定风速以上时，控制桨距角β，减小风能利用系数，保证稳定的功率输出。

1.2 风轮迎风平面内风速特性分析

影响风速变化的原因有很多，除了风轮的布局、体形等因素外，高度的变化对风速也有着显著的影响[5]。地面垂直高度增加，风速也随之增加，只有高于300m时风速才不会受这些因素影响。风速在垂直高度的变化主要受风切效应和塔影效应影响[6]。

图1 风力机风能利用系数CP(λ,β)的特性曲线

风剪切是稳定状态下平均风速随着高度的变化而变化。假设地面为零风速平面，则有风切公式为：

(4)

式中n——风剪切系数，它取决于大气和地面的客观因素，一般情况下取0.1～0.4；

νH——距地面H高度处的风速；

νH0——距地面H0高度处的风速。

在塔架的上游和下游，塔架对气流的阻塞使风流速度减少，称为塔影效应。对于上风向风力发电机，在塔影坐标系下某点上垂直于风力机风轮旋转面的风速可以表示为：

(5)

式中ht——塔架在某点的塔架高度；

Rt——塔架半径；

xt，yt——塔架坐标系下的水平两个方向坐标；

Y——塔径修正因子。

在风力机风轮旋转平面内，如果该点的桨叶方位角沿中心相对于轮毂中心在之间，则式(5)成立。

1.3 基于桨叶方位角权系数分配的独立变桨距控制

设计基于桨叶方位角权系数分配的独立变桨距控制系统，在统一变桨距基础上进行风力机各个桨叶桨距角的独立调节，减少由风切效应和塔影效应引起的风力机桨叶的不均匀载荷，使输出功率稳定输出，延长风力机的使用时间。

风轮旋转平面内的风速分布是不均匀的，高度对风速的影响最为显著，风速在垂直高度上的变化主要是由风切和塔影效应导致的，可以根据桨叶所处风轮旋转平面的位置来确定吹向桨叶的风速大小[7]。设水平面轴线为x轴，桨叶的旋转方向以逆时针方向为正，桨叶的中心线与x轴之间的夹角θ定义为桨叶的方位角，可以通过桨叶的方位角来确定桨叶的具体位置。选定一个桨叶作为基准叶片，桨叶1的方位角θ作为起始方位角，则桨叶2的方位角为θ+120°，桨叶3的方位角为θ+240°。根据规定每个桨叶所受的平均风速是桨叶的中心位置，其平均风速为：

(6)

式中i——第i个桨叶，i=1,2,3；

ν——传感器所测风速；

νi——每个桨叶所受平均风速；

θ——桨叶1的方位角。

基于桨叶方位角权系数分配的独立变桨距控制的思路(图2)：当风速高于额定风速时，首先运用变桨距控制器进行统一变桨距控制，得到风力机3个叶片统一变桨距的桨距角；然后根据桨叶方位角得到权系数重新分配每个桨叶的桨距角，实现独立变桨距控制。

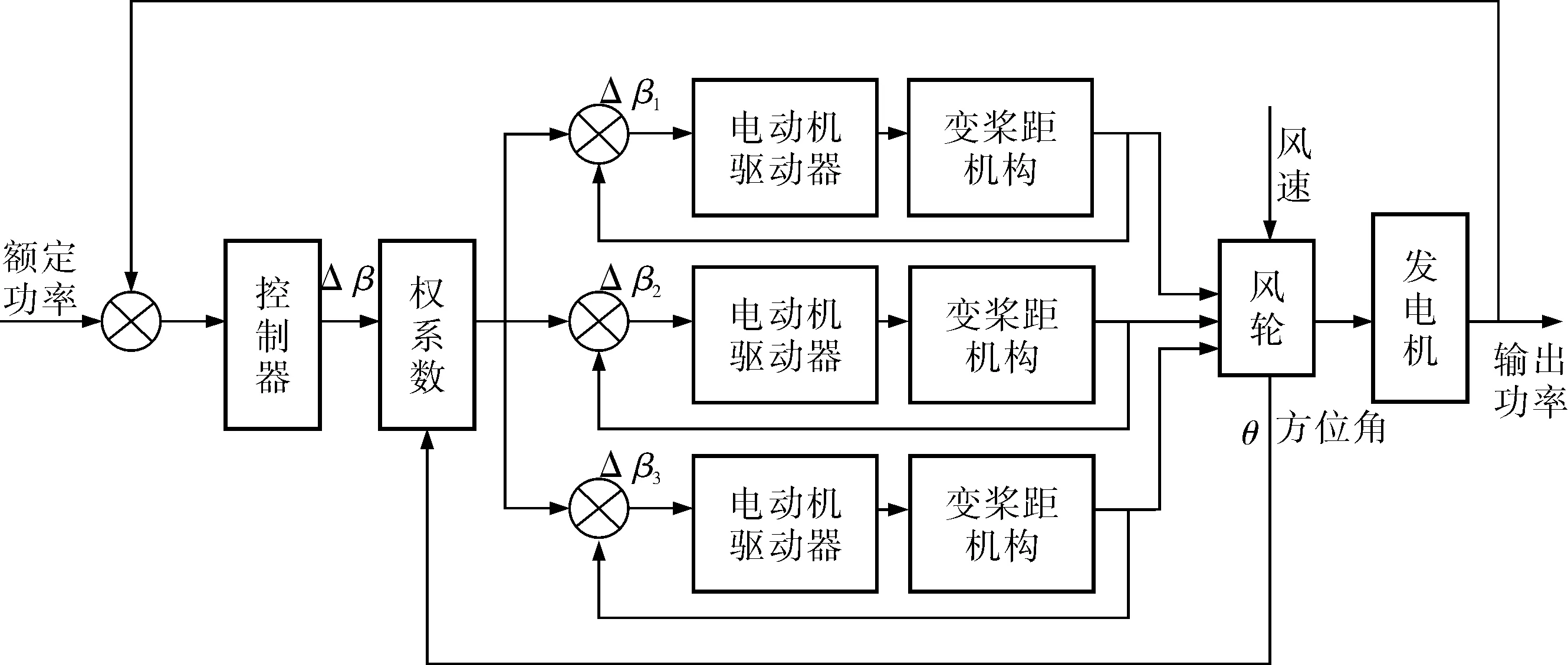
图2 独立变桨距控制系统

权系数是根据风力机每个桨叶的受风情况来分配的。权系数随风速的变大而变大，桨距角随权系数的增大而增大。其分配过程是根据每个桨叶的方位角θi设权系数Ki(i=1,2,3)，通过权系数将3个桨叶统一变化的桨距角Δβ进行分配，转化为每个桨叶独自变化的桨距角Δβi。

(7)

桨叶方位角权系数Ki的计算式为：

(8)

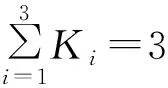
2 变桨距控制器的设计

2.1 模糊PID控制器的不足

在控制策略的研究中，模糊PID控制的控制效果比传统PID控制及模糊控制等的控制效果好。模糊PID控制是模糊控制与常规PID控制算法相结合的一种新型控制方法，找出PID 3个参数与误差、误差变化率之间的模糊关系，建立模糊规则，在运行中不断检测误差和误差变化率，根据确定的模糊规则对3个参数进行在线实时整定，满足不同误差和误差变化率对3个参数的不同要求。

大多数模糊推理只着重不确定性现象和事物中的模糊性，未能考虑不确定性现象和事物的随机误差，推理系统输入值有很大随机性。由于模糊控制要确定精确的隶属度函数，因此容易造成推理结果错误。

2.2 云模型

云模型是定性概念和定量表示之间的不确定性转换模型，主要反映知识表示中的两种不确定性。在众多不确定性中，最基本和最重要的是模糊性和随机性，针对概率论、模糊数学在处理不确定性方面的不足，研究了模糊性和随机性两者之间的关系[8]。

云的定义：设U是一个用精确数值表示的定量论域，A是U上的定性概念，若定量值x∈U，且x是定性概念A的一次随机实现，x对A的隶属度μ(x)∈[0,1]具有稳定倾向的随机数，则称μA(x)在U上的分布为云模型。

2.3 基于云模型的模糊推理PID控制器

笔者设计的控制器是将正态云模型引入到隶属度函数，用正态云函数表示隶属度，构成基于云模型的模糊推理PID控制器，可以兼顾模糊性和随机性[9]，控制器结构如图3所示。

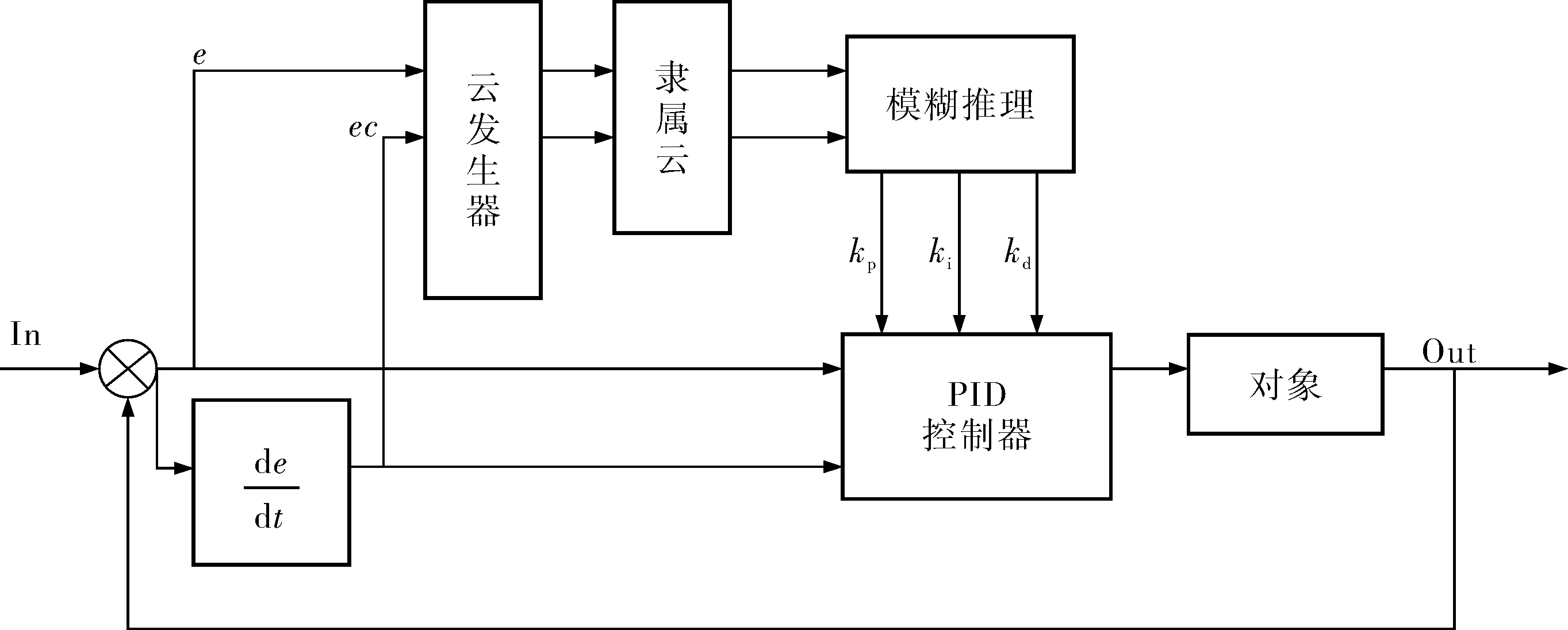
图3 云模型模糊推理PID控制器结构框图

正态云是一种是一种普通的适用云。设R1(E1,E2)表示服从一维正态分布的随机函数，其中E1为期望值，E2为标准差，则有：

xi=R1(Ex,En)

Pi=R1(En,He)

由满足上式的数据点(xi,μi)(i=1，2，…)构成的云模型称为一维正态云模型，式中Ex、En、He是该云模型的3个重要数字特征，分别称为一维云模型的期望、熵和超熵。

正态云发生器是由云的数学特征产生云滴的过程，如图4所示。

图4 正态云发生器的形成

在模糊控制规则中，误差为e、误差变化率为ec，修正系数为kp，ki，kd，模糊子集为{NB，NM，NS，ZO，PS，PM，PB}，论域为e={-30，30}、ec={-60，60}。基于云模型的模糊推理PID控制器是以误差e和误差变化率ec作为输入，将正态云模型引入模糊控制的隶属度函数，根据每个正态云模型的隶属度函数设计PID参数的模糊矩阵表，利用模糊规则进行模糊推理，查询模糊矩阵表在线对PID参数进行调整。

图5 正态云模型

3 仿真分析

RT-LAB是一种全新、可扩展的基于模型的工程设计应用实时仿真平台。通过RT-LAB可以直接利用Matlab/Simulink建立动态数学模型进行实时仿真。笔者运用RT-LAB仿真实验平台进行仿真验证，根据RT-LAB建模方法建立风力发电系统模型，如图6所示。

图6 RT-LAB下搭建风力发电系统及SC、SM子系统

笔者以1.5MW变桨距风力发电机组为研究对象，在高于额定风速取初始风速为13m/s，20s时突变到14m/s。对模糊PID控制和云模型控制方法进行仿真比较，如图7～9所示。

图7 模糊PID统一变桨距控制的输出功率曲线

图8 模糊PID独立变桨距控制的输出功率曲线

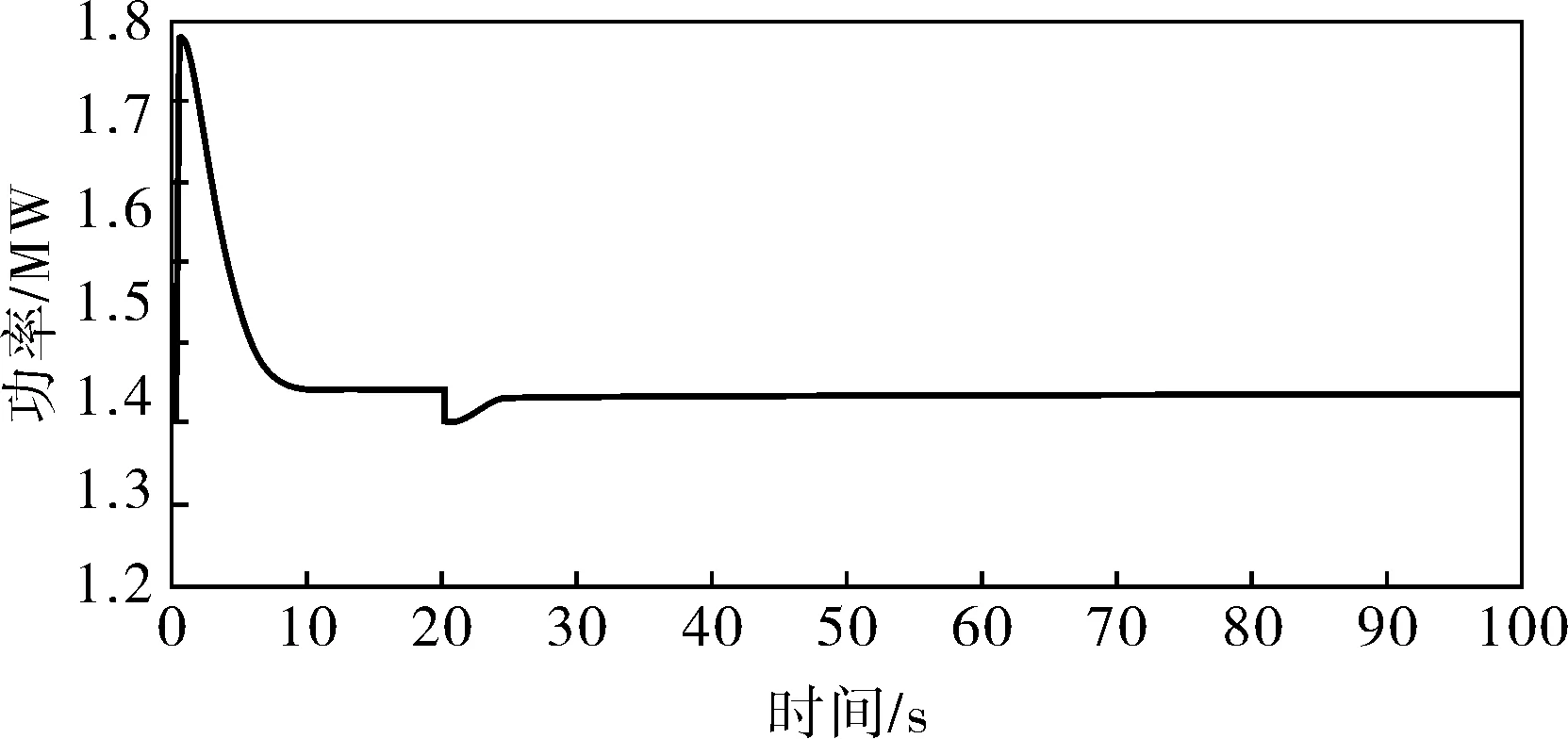
图9 基于云模型的独立变桨距控制的输出功率曲线

仿真结果表明，在高于额定风速时，统一变桨距和独立变桨距控制都能控制输出功率稳定在额定功率附近，且在风速变化时也有较好的控制效果，但独立变桨距控制的超调更小，稳定性更高。基于云模型的独立变桨距控制比基于模糊PID的独立变桨距控制效果更好，超调更小，响应速度更快，稳定性更好，控制效果更加理想。

4 结束语

分析了风电机组变桨距控制系统的运行特性和风切、塔影效应对风速的影响，并详细介绍了云模型的概念和特征。采用方位角权系数分配的方法，设计了基于云模型的独立变桨距控制系统，运用RT-LAB仿真实验平台对1.5MW风力发电机组进行建模仿真。仿真结果表明：在高于额定风速时，该系统超调小，响应速度快，稳定性强，可以有稳定的功率输出，实现了系统的优化运行，取得了理想的控制效果。