冷连轧机厚控系统的PI型广义预测控制

梁秀霞 王 萌 张 强 赵羽佳 李金松

(河北工业大学控制科学与工程学院，天津 300130)

冷轧带钢生产过程中，自动厚度控制系统对成品带钢的质量有很大影响。厚度控制的目的就是通过调节辊缝、张力及电机速度等参数，消除轧制过程中影响厚度精度的因素[1]，提高厚度控制精度，满足工业生产需求。

目前，冷连轧自动厚度控制系统一般采用解耦控制，即PID控制外加各种补偿。但是冷轧机自动厚度控制系统的强耦合、非线性及大延时等特性，使得传统的PID控制不能取得很好的控制效果。广义预测控制(Generalized Predictive Control，GPC)是由Clarke等人于1984年提出的，是基于自适应的研究发展而来的，GPC在广义最小方差控制的基础上，引入了多步预测和滚动优化的思想，使其对有扰动、有噪声和时延大的系统有很好的控制效果。具有PID结构的广义预测控制器，通过将GPC的目标函数改成PID型，就可以利用PID反馈信息改善系统性能，但PID型GPC计算量很大，因而笔者将引入简化的PI型GPC，以减少计算量；同时利用GPC预测信息抑制超调，提高系统稳定性。结合两者的优点，得到PI型广义预测算法(PIGPC)。

1 PIGPC控制器①

1.1 PIGPC控制原理

PIGPC借助智能控制策略改善传统PI控制的性能，又能对GPC控制的不可控超调起到抑制作用。GPC可以在模型反馈信息的基础上多步预测、滚动优化，这使得该控制策略对建模误差及环境干扰等不确定性影响有很强的适应能力。PIGPC结构如图1所示。

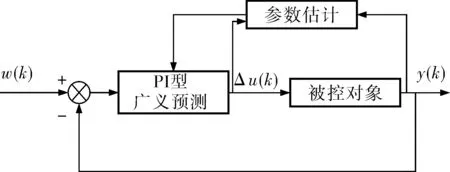
图1 PIGPC结构框图

1.2 GPC控制器模型

基于广义预测受控自回归积分滑动平均模型(CARIMA)构建的冷轧带钢厚度系统模型为：

A(z-1)y(t)=z-dB(z-1)u(t-1)+C(z-1)ξ(t)/Δ

A(Z-1)=1+a1z-1+…+anz-na

B(Z-1)=b0+b1z-1+…+bnz-nb

C(Z-1)=1+c1z-1+…+cnz-nc

Δ=1-z-1，为差分算子；y(t)、u(t)和ξ(t)分别为系统的输出量、输入量和正态白噪声干扰，d为延时步长。{ai}、{bi}和{ci}分别为多项式A、B和C的系数，na、nb和nc对应其阶次。

标准广义预测控制的目标函数为：

其中，E为数学期望；N表示预测时域；M表示控制时域；λ(j)为输出预测误差与控制加权系数，通常为简化计算设其为常数λ[2]，λ>0，1≤M≤N，当j=M+1,M+2，…,N时，Δu(t+j-1)=0;{w(t)}为设定值参考序列，其数值可由下式计算：

式中yr(t)——t时刻的设定值；

η——柔化因子，0≤η<1。

1.3 PIGPC控制器

设误差序列e(t+j)=w(t+j)-y(t+j)，在广义预测控制的目标函数中加入PI参数可得：

(1)

其中e(t)=Δe(t)=0，KP为比例项系数，KI为积分项系数。

对其进行计算推导后[3，4]，式(1)可表示为：

J(t)=E(KPΔeTΔe+KIeTe+λΔUTΔU)

ΔU(t)=[Δu(t),Δu(t+1),…,Δu(t+N-1)]T

(2)

将J对未知控制增量矢量ΔU求导，并令∂J/∂u=0，可得控制规律为：

(3)

当采用即时PIGPC控制策略时，可取KP和KI的首行得到：

(4)

kP=[1,0,…,0]KP,KI=[1,0,…,0]KI

1.4 简化的PIGPC控制器

PIGPC控制相较PID计算量有所减少，但计算量仍是不可忽略的因素。这里使用简化的PIGPC控制，并使用柔化系统输入，避免矩阵逆运算，以大幅减少计算量。

PIGPC控制的积分部分是与传统GPC控制中的预测输出和实际输出的差值相对应的，比例环节和积分环节的引入可以使响应曲线更加平滑，基于此，将式(1)简化为：

(5)

将其改成矩阵形式，可表示为：

J(t)=KpΔeTΔe+KIeTe+λΔUTΔU

(6)

e=yr-f-GiΔU(t)

Δe=Δyr-Δf-GpΔU(t)

e=[e(t+d+1),e(t+d+2),…,e(t+d+N)]

Δe=Δe(t+d+2)=e(t+d+2)-c(t+d+1)

yr=[yr(t+d+1),yr(t+d+2),…,yr(t+N)]

Δyr=Δyr(t+d+2)

f=[f(t+d+1),f(t+d+2),…,f(t+N)]

为了进一步减少计算量，提高整个算法的实时性，引进柔化系统输入的阶梯型算法[5]：

ΔU(t)=LΔu(t)

(7)

将式(7)代入式(6)并对二次型指标求最小值，可得：

(8)

由式(8)可以看出，当前最优控制增量中不包含矩阵的求逆运算，同时比例环节只使用了单步的值，这就减少了计算量，提高了控制的实时性。

2 冷连轧机厚控系统数学模型

冷连轧机采用的是外环为厚度控制、内环为辊缝控制的双闭环控制方式。自动厚度控制系统(Automatic Gauge Control，AGC)的执行系统为自动位置控制系统(Automatic Position Control，APC)，是AGC系统的内环，APC系统由位移传感器测量液压缸位移量或测量轧辊辊缝的位移量构成反馈闭环控制。APC主要由伺服阀、液压缸和伺服放大器组成。对其进行设计并且调整其参数，可以整定成一个二阶振荡环节[6]：

(9)

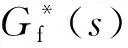
从轧机工作辊缝Gf(s)到冷连轧带钢出口的厚度h(s)为厚控系统的外环部分，其传递函数可以近似表示为：

(10)

其中，TI为惯性时间常数；系数K0随轧制道次、轧制带材的塑性刚度、种类及来料厚度等因素的变化而变化，在薄带钢轧制过程中，K0一般取值在0.9～2.0之间；τ为测厚仪检测滞后时间常数，τ=L/v，L为测厚仪到轧机中心线的距离,v为带钢轧制速度。

3 仿真分析

为了检验简化PIGPC的控制效果，选用传统PI控制、GPC控制和简化PIGPC控制，通过仿真图形对比，验证新的控制策略在冷连轧厚度控制系统中的控制效果。将某钢厂1 450mm冷连轧机厚度控制系统的参数ξ=0.9、ωn=28.8rad/s、TI=0.25、K0=1.2、τ=0.6s代入式(9)、(10)，得到该系统的传递函数：

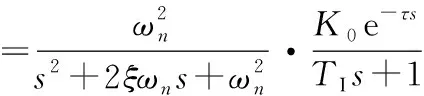
(11)

对于该系统的PI控制仿真采用的是Matlab的Simulink工具箱，直接调用相关功能块即可实现(图2)。由于Simulink中没有广义预测控制相关的功能块，所以PIGPC的仿真是以M文件的形式实现的。

图2 PI控制系统仿真模型

在PID模块中设置参数：P=0.5，I=0.8，按图2模型仿真得到如图3所示的曲线。

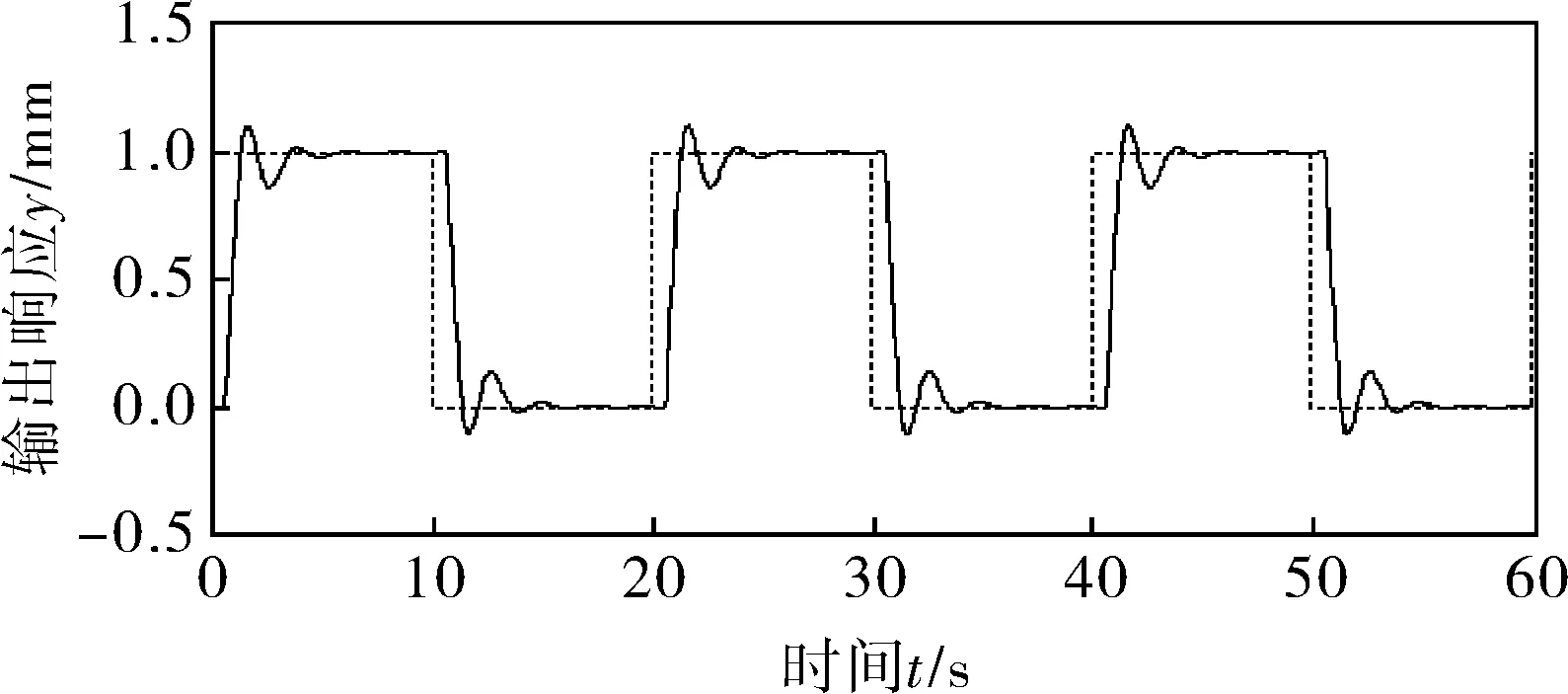
图3 PID控制仿真结果

可以看出，传统的PI控制超调较大，调节时间长，控制效果不尽如人意。PIGPC需要设定的参数比较多，有KP、KI、λ、η、β、N及M等，KP和KI增大，系统动态性能提高，响应速度加快，但会加剧超调，稳定性下降；N增大，提高了系统的稳定性和鲁棒性，但响应速度变慢；M增大，改善了跟踪性能，提高了控制灵敏度，但稳定性和鲁棒性降低；λ的作用是限制控制增量的剧烈变化，λ越大，限制作用越明显；η增大，跟踪速度变慢，超调量减小。为了达到令人满意的控制效果，需要平衡各参数间的关系，为突出相同条件下的不同控制效果，参数设为：N=10、M=3、λ=0.3、η=0.2、KP=1.8、KI=0.8、β=0.5，所得GPC控制仿真曲线如图4所示，可以看出，GPC难以抑制系统超调，仿真时间为0.604s。

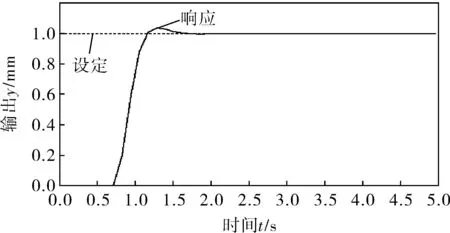
图4 GPC控制仿真结果

相同参数下，PIGPC的控制曲线如图5所示。由仿真曲线可以看出，PIGPC能很好地抑制系统超调，但计算量较大，仿真时间为0.749s。

图5 PIGPC控制仿真结果

相同参数下，简化PIGPC控制曲线如图6所示，由仿真曲线可以看出，简化PIGPC能很好地抑制系统超调，计算量减小，仿真时间仅为0.652s。

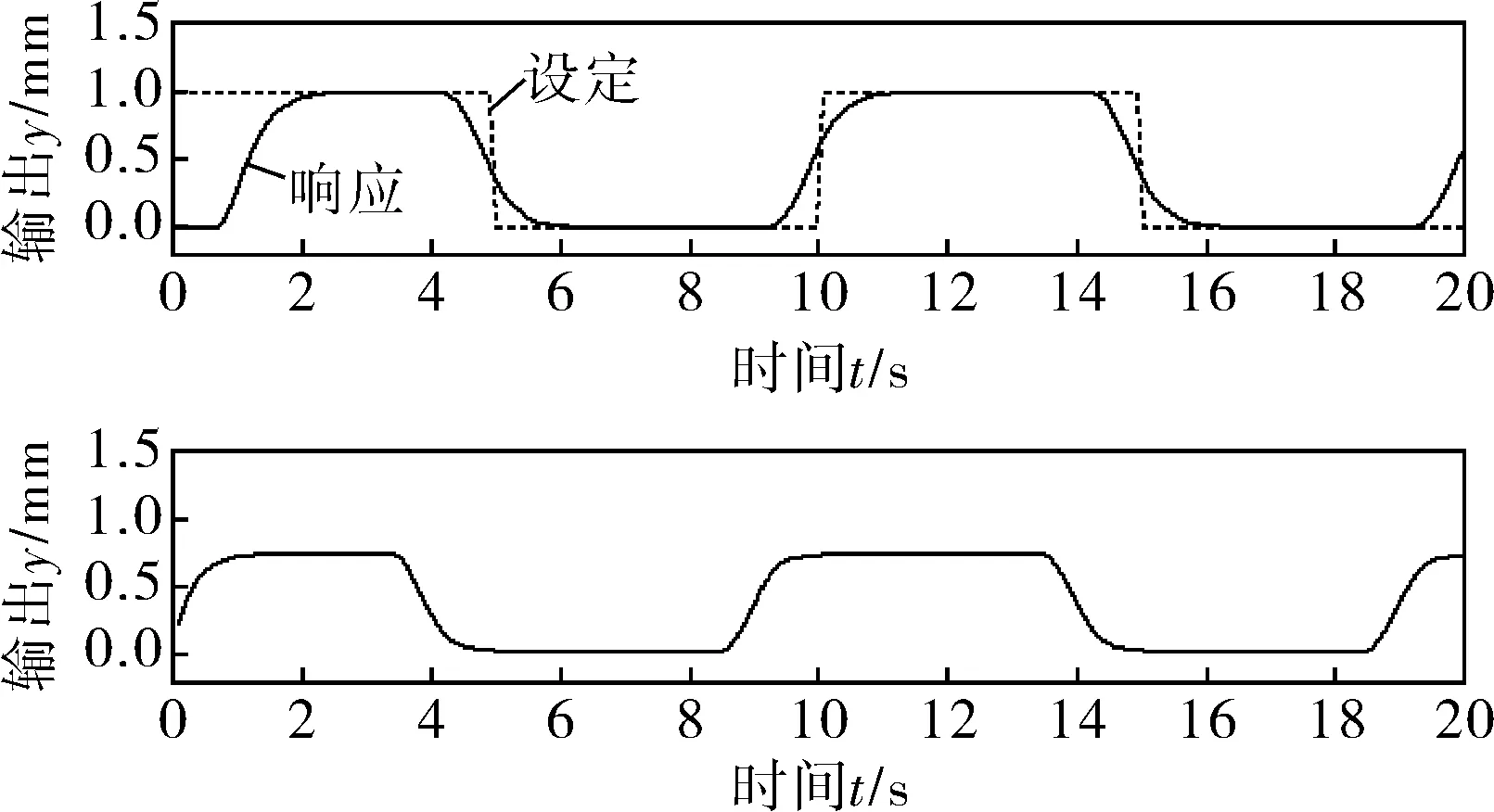
图6 简化PIGPC控制仿真结果

对比仿真图像可以看出，简化PIGPC控制方式相比传统PID控制，能提高系统稳定，具有更好的跟踪性能和更高的控制精度；相比GPC控制，能较好地抑制超调，改善控制品质，计算量增加不大，实时性较高，适合在工业现场使用，使得冷轧带钢具有更高的厚度精度。

4 结束语

基于广义预测控制理论，与经典PI控制相结合，设计了用于冷连轧机厚控系统的简化PIGPC控制策略，充分地利用了GPC的预测信息调节了控制量。通过仿真结果的对比可以看出：简化PIGPC能很好地抑制超调，具有更好的动态性能和跟踪速度快，其控制精度有所提高。