基于改进人工势场法的AUV路径规划

吴正平 唐 念 陈永亮 喻高明 俞 辉

(1.三峡大学 a.电气与新能源学院;b.理学院，湖北 宜昌 443002；2.长江大学石油工程学院，武汉 430100)

路径规划是自主式水下航行器(AUV)研究的重要课题，路径规划技术是决定AUV智能水平的关键技术。AUV路径规划指：AUV在有障碍物的环境中，寻找一条从起点到目标点的安全无碰路径，并要求时间尽可能最短。路径规划方法有很多种，常见的有栅格法、可视图法、遗传算法、蚁群算法、人工势场法及流函数法等[1]。笔者提出一种基于改进人工势场法的AUV路径规划方法。

1 人工势场法的基本原理①

人工势场法的基本原理为：把AUV当作质点，假设AUV在一个存在复合势场的环境中运行，在此环境中障碍物周围有斥力场，目标点处有引力场[2]。建立关于距离的势函数，AUV所受的力即虚拟的势场力。虚拟的势场力就是势的负梯度[2]。AUV在虚拟的势场力的作用下，从起点绕过障碍物运动到目标点。

1.1 势函数

设复合势场为U(R)，目标点引力场为Ua(R)，障碍物的斥力场为Ur(R)，则有U(R)=Ua(R)+Ur(R)。引力和斥力分别为引力场和斥力场的负梯度，故引力和斥力分别为Fa(R)=-grad[Ua(R)]、Fr(R)=-grad[Ur(R)]，则AUV所受的作用力为F(R)=Fa(R)+Fr(R)。将AUV看作质点，假设其在一个二维位姿空间内运动[2]，AUV的位置表示为R=[x,y]T。建立关于距离的势函数，则引力势函数为：

(1)

其中k为引力势场因子，k>0；R为AUV的位置向量；Rg为目标位置；ρ(R,Rg)为AUV和目标点之间的距离，ρ(R，Rg)=‖Rg-R‖；ρ2表示目标点对AUV的引力势场是一条抛物线。

障碍物对AUV的斥力势函数为：

(2)

其中η为斥力势场因子，η>0；ρ(R,Rg)为AUV与障碍物的最小距离；ρ0为单个障碍物的影响距离，ρ0>0，当AUV与障碍物的距离大于ρ0时斥力势场对AUV的运动不再有影响。

总的势场U的计算式为：

(3)

1.2 AUV受力分析

人工势场法AUV受力分析如图1所示。

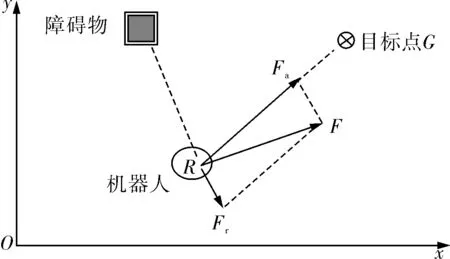
图1 人工势场法AUV受力分析

目标位置对AUV的吸引力为：

Fa(R)=-▽Ua(R)=k(Rg-R)

(4)

障碍物对AUV的斥力为：

(5)

故AUV受的总合力为：

(6)

1.3 人工势场法的缺点

人工势场法算法简单，但存在以下缺点[2]：

a. 局部极小值问题。当AUV所处的位姿环境比较复杂，障碍物数目较多时或者进入“死胡同”(例如U形障碍物)时，就容易陷入局部极小。

b. 在相隔很近的障碍物之间发现不了路径。当AUV运动到靠近两障碍物中间，并且此时AUV所受的引力约等于AUV所受的斥力时，AUV的速度为0，AUV就会停滞不前。

c. 当目标点附近有障碍物时无法到达目标点。当AUV的目标点附近有障碍物并且在该点时AUV所受的合力的方向背离目标点，即AUV所受的斥力大于目标点对AUV的引力，这种情况下AUV无法到达目标点。

2 改进的人工势场的路径规划算法

新的斥力场函数为：

(7)

ρn(R,Rg)为AUV和障碍物之间的最小距离，ρn(R,Rg)的引入能够确保目标点处的总势场达到全局最小。当ρ(R,Rg)不为0，即AUV还未到达目标点时，此时的斥力为：

(8)

▽ρ(R,R0)和-▽ρ(R,Rg)是两个单位向量，前者表明斥力Fr1的方向由障碍物指向AUV，后者表明Fr2的方向是由AUV指向目标位置。当AUV在海洋环境运动时，假定海流对AUV的作用力为恒力，则AUV的受力情况变为：

F(R)=Fa(R)+Fr(R)+Fwav(R)

(9)

改进人工势场法AUV受力分析如图2所示。

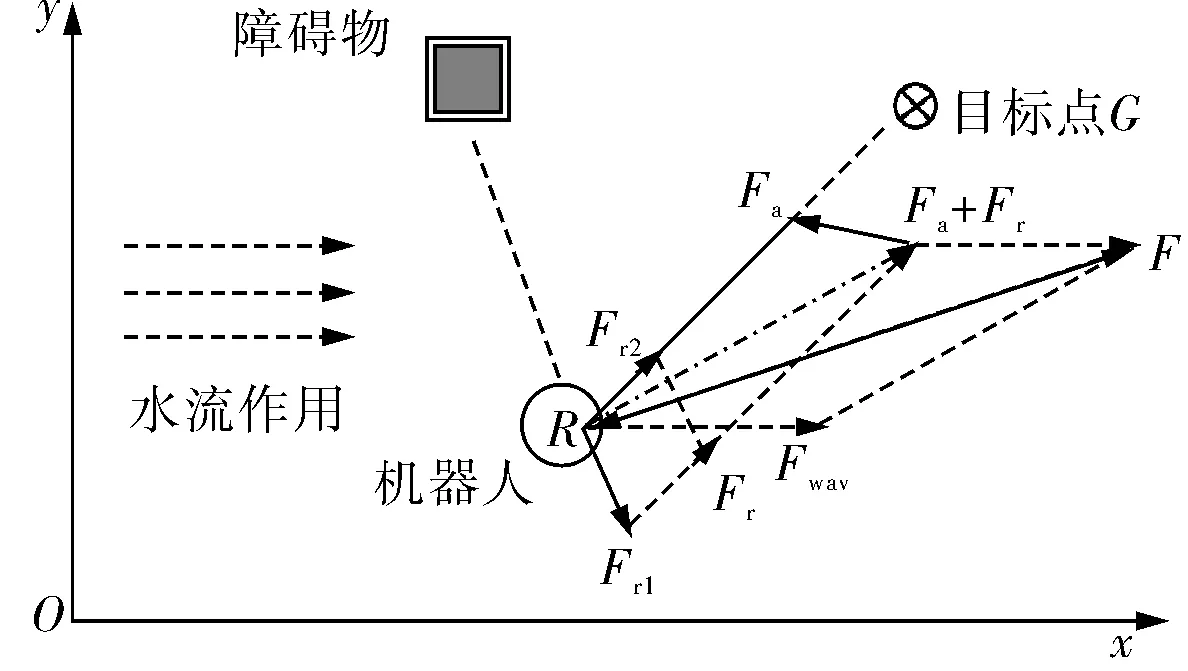
图2 改进人工势场法AUV受力分析

3 实验结果分析

使用Visual Studio 2005 编程，对改进的人工势场法进行仿真实验，仿真结果如图3所示。

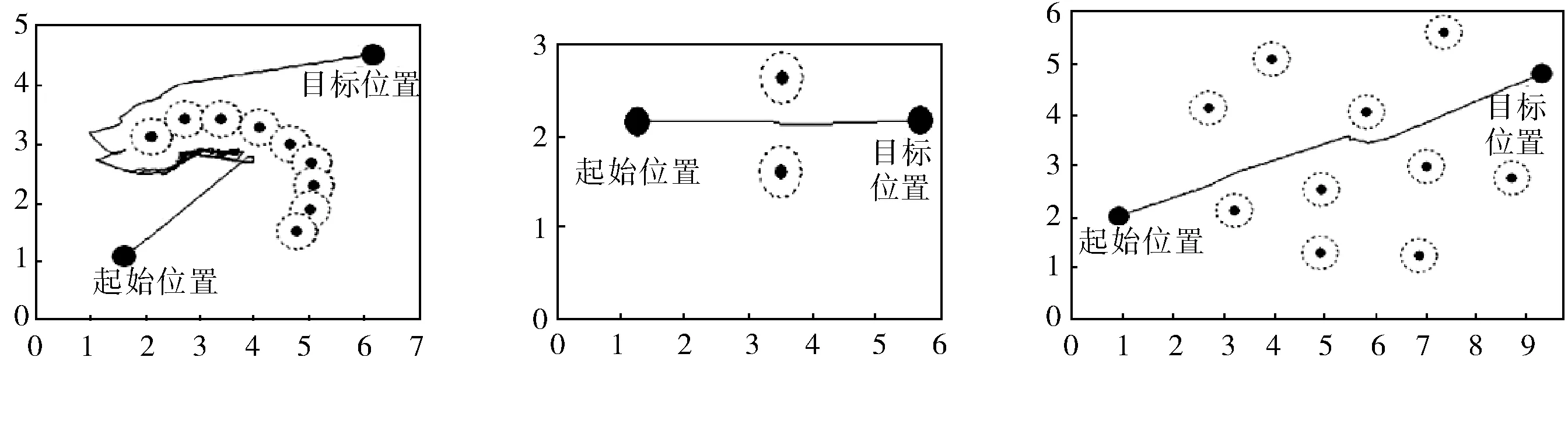
图3 AUV运动仿真

仿真结果表明：

a. 当AUV进入“死胡同”(例如U形障碍物)时，先会在某一时间内产生振荡，然后再绕过障碍物，顺着一条可行的路径到达目标点，而不会在U形障碍物内停滞不前。

b. 当两障碍物相隔很近时，AUV能够在两个障碍物之间找到路径顺利到达目标位置。

c. 当目标点附近有障碍物，并且在障碍物的影响范围之内时，AUV能够顺利到达目标位置。

4 结束语

人工势场法由于计算简单、反应速度快并且易于实现和扩展，因此在AUV实时路径规划中应用非常广泛。但是人工势场法也有一定的缺陷，笔者将改进的方法运用在自行研制的AUV上进行实验，结果表明：改进的方法效果较为明显，能够克服传统人工势场法存在的部分缺陷。