焦炉集气管系的智能解耦与仿真研究
张缓缓 朱斌祥 李金荣 赵宗彬
(合肥通用机械研究院,合肥 230031)
炼焦生产过程中,会产生大量的焦炉煤气。集气管主要用于将荒煤气汇集并引导至后续环节。焦炉集气管系是高度复杂的工业系统,数学模型建立困难,各集气管间耦合严重[1]。集气管压力是炼焦生产的关键技术参数,集气管压力的大幅波动不仅影响炼焦产品的质量,还会造成环境污染和能源浪费,甚至影响焦炉的使用寿命[2]。应用先进的智能控制技术进行集气管系的解耦,是实现焦炉集气管压力精确控制的前提和基础。
1 控制对象特性分析与建模①
1.1 控制对象特性分析
焦炉集气管系是复杂的多变量耦合系统。以某焦化厂3座焦炉为例,该焦化系统3座焦炉共用一套初冷和鼓风系统[3]。距离较近的1#和3#为Ⅰ组,2#焦炉单独为Ⅱ组。Ⅰ组组内连接管道很短,两组间的连接管道较长,集气管总管的连接管道最长。焦炉集气管系的工艺流程如图1所示。
3座焦炉并联连接,各集气管之间为负耦合关系[4]。组内集气管间并联管道较短,耦合关系较强,自平衡较快;而组间集气管并联管道较长,耦合关系相对较弱,自平衡也较慢。这些耦合现象会使系统超调和振荡现象严重,降低系统的控制效果,严重时甚至使系统无法运行,对正常的炼焦生产造成恶劣的影响[5]。
1.2 系统数学建模
在集气管系的管道中,流体的阻力除一部分在管道上,多数集中在蝶阀上。蝶阀的阻力系数R与其开度有关。在建模的过程中,考虑到气体的可压缩性,对气体的体积流量和气体压力间的关系应予以充分考虑。
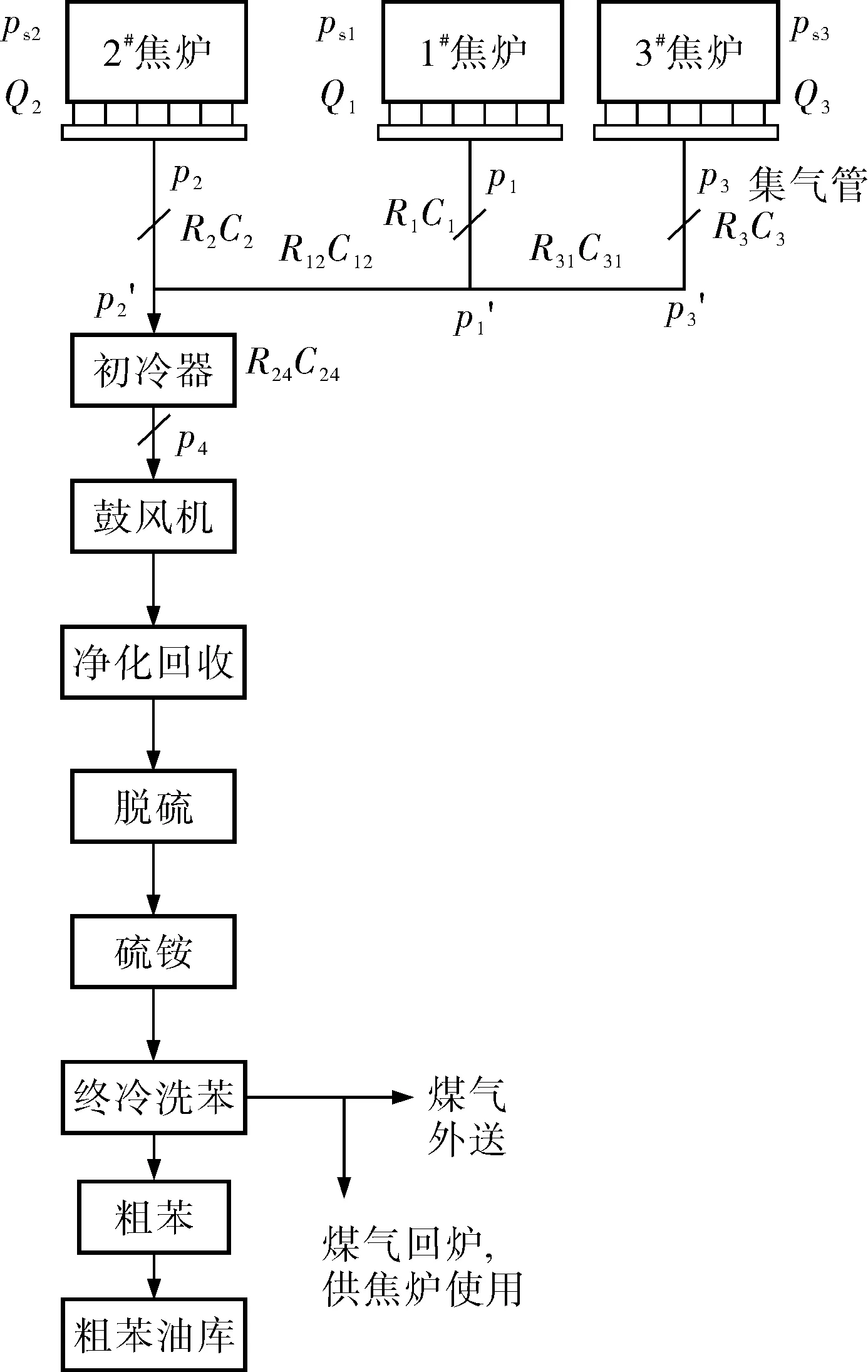
图1 焦炉集气管系的工艺流程
C1、C2、C3、C12、C31、C24——对象的容量系数;
p1、p2、p3——集气管的煤气压力;
p4——鼓风机前压力;
p1′、p2′、p3′——集气管后煤气压力;
ps1、ps2、ps3——产出煤气的压力;
Q1、Q2、Q3——进入集气管的煤气流量;
R1、R2、R3、R31、R12、R24——对象的阻力系数
建模中,对象的控制输入为R1、R2和R3;对象的扰动输入为ps1、ps2、ps3和p4;系统输出为p1、p2和p3。对象的阻力系数R=dp/dQ,对象的容量系数C=dV/dp。由dQ=dV/dt得到dQ=C·dp/dt。由气体流量动态平衡方程dQ=Q入-Q出,可得dQ=Q入-Q出=C·dp/dt。由此,建立各集气管的气体动态平衡方程:
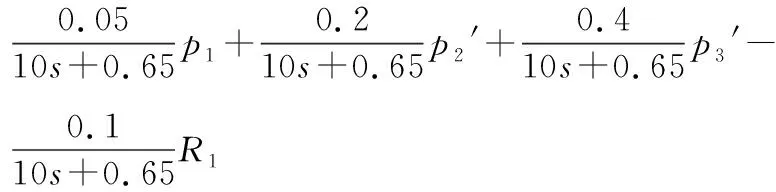
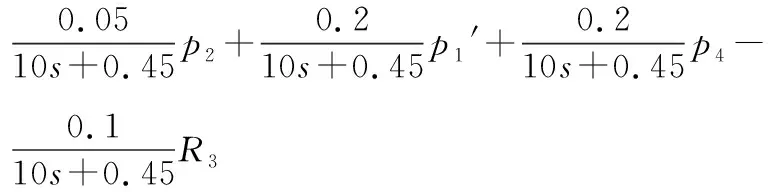
2 智能解耦系统设计
2.1 总体设计
3座焦炉集气管系的解耦方案要求能够较大程度地减弱甚至消除3座焦炉集气管间的耦合作用。笔者采用模糊控制原理进行3座焦炉集气管系的模糊解耦控制器设计。模糊控制能不依赖被控对象的精确数学模型,具有控制性能高、能够针对非线性复杂对象且鲁棒性能好的优点[6]。
依据模糊控制原理,首先将Ⅰ组进行组内解耦,组内解耦输出控制增量的修正值。再将Ⅱ组与Ⅰ组进行组间解耦,组间解耦输出控制增量的二次修正值。图2为焦炉集气管系智能解耦系统解耦示意图。

图2 焦炉集气管系智能解耦系统解耦示意图
2.2 组内解耦
集气管各个回路的控制增量能够反映出压力的波动,因此,输入语言变量选取1#和3#集气管两个单回路控制的控制增量ΔU1和ΔU3,输出语言变量选取控制增量的修正值V1和V3。V1、V3的组内解耦规则见表1。

表1 V1、V3的组内模糊解耦规则
控制器采用重心法进行模糊判决,计算公式为:
u=∑xi·μN(xi)/∑μN(xi)
2.3 组间解耦
组间解耦是对控制增量进行的二次修正。设经组内解耦修正后各集气管压力控制增量的语言值分别为ΔU1′、ΔU2和ΔU3′,取:
ΔUZ2=ΔU2
组间解耦控制的输入量取为ΔUZ1和ΔUZ2,输出语言值设为W1和W2,是控制增量的二次修正量。W1、W2的组内模糊解耦规则见表2。
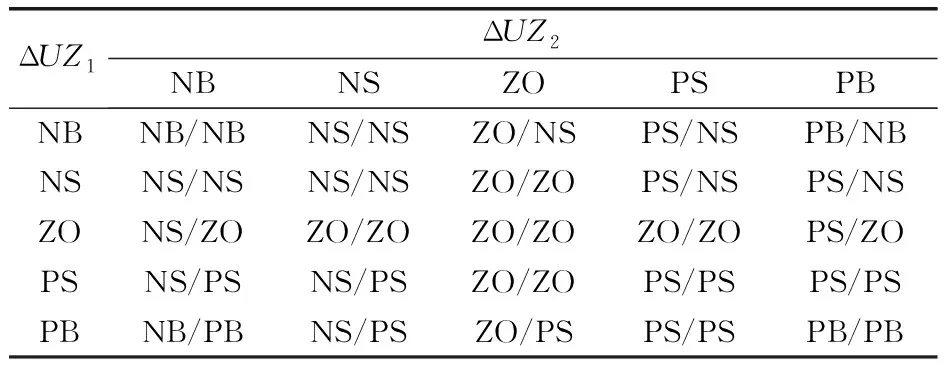
表2 W1、W2的组内模糊解耦规则
控制器采用重心法进行模糊判决。设语言变量W1、W2的输出量为w1、w2,单回路控制输出的控制增量Δu1和Δu3经组内和组间解耦控制修正后的蝶阀控制增量为:
Δu1″=Δu1′+w1=Δu1+v1+w1
Δu2″=Δu2+w2
Δu3″=Δu3′+w1=Δu3+v1+w1
3 仿真与结果分析
3.1 系统数学模型仿真及验证
利用Matlab/Simulink对焦炉集气管系数学模型进行仿真实验,建立系统的仿真实验模型。对系统仿真模型,分别给R1、R2、R3突加阶跃信号(在其他输入均为零的前提下),可得到各自的阶跃响应曲线。
以R1=10为例进行分析,R1=10时的阶跃响应曲线如图3所示,当R1增大时,压力p1升高,压力p2和p3降低,p2降低的幅度比p3降低的幅度小。实际中,当阻力系数R1增大,即1#集气管蝶阀开度减小时,1#集气管压力增大,2#、3#集气管压力都会减小,且离1#集气管较近的3#集气管压力减小的幅度更大。仿真结果与实际符合。
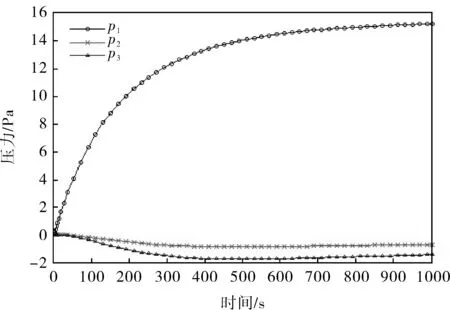
图3 R1=10时的阶跃响应曲线
3.2 模糊智能解耦系统的仿真
根据3座不对称焦炉集气管系的解耦控制方案,利用Simulink建立组内、组间解耦控制的仿真模型。对解耦仿真模型分别给控制量R1、R2、R3突加阶跃信号(其他输入均为零的前提下),得到仿真结果如图4~6所示,经过组内、组间解耦后,任一集气管蝶阀动作时,其他集气管压力波动非常小,且能较快稳定到零点,各集气管之间的耦合作用几乎被完全消除。可见,系统的智能模糊解耦方案能够达到理想的解耦效果。
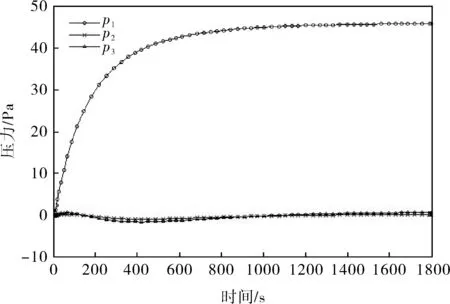
图4 R1=30时的阶跃响应曲线
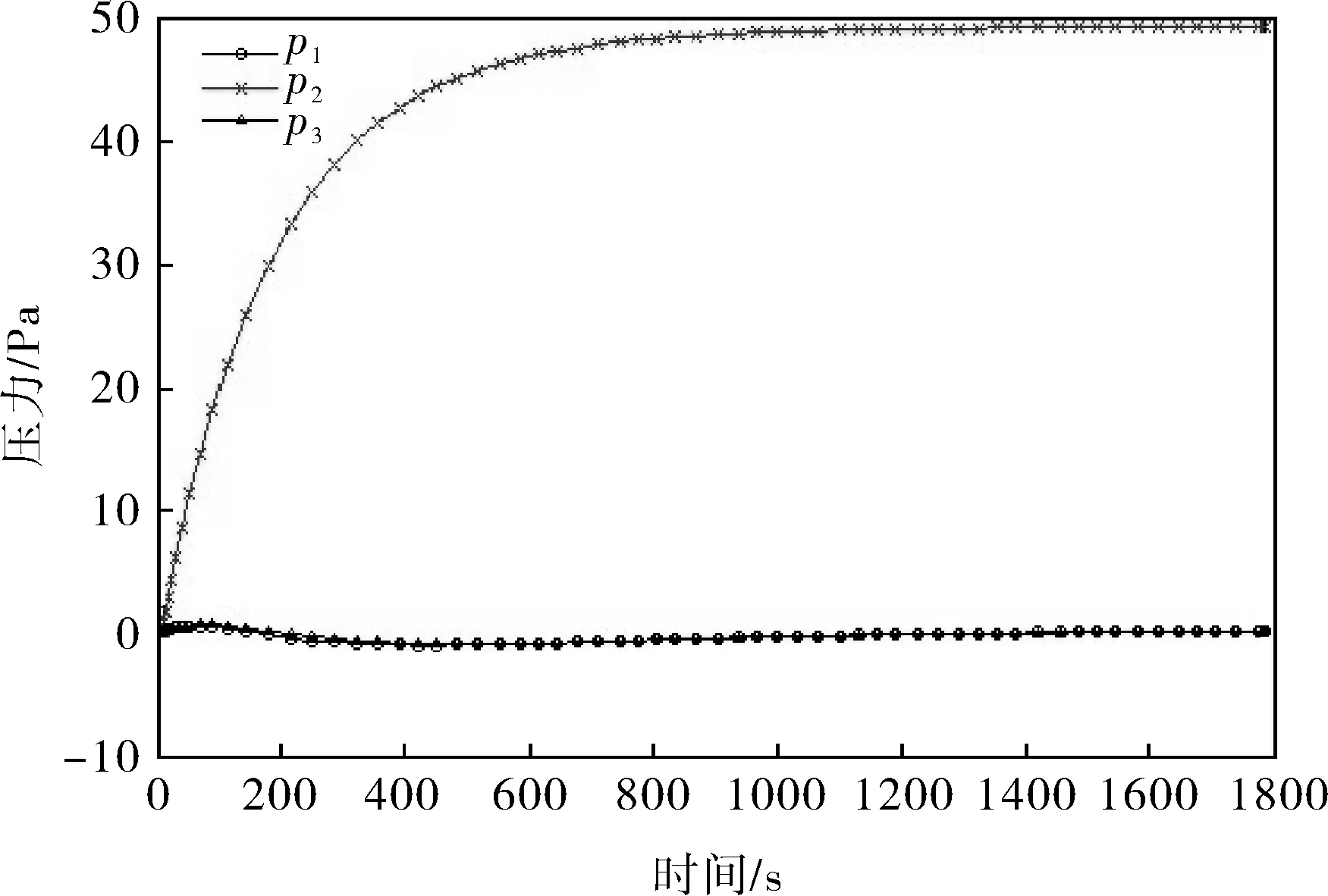
图5 R2=30时的阶跃响应曲线
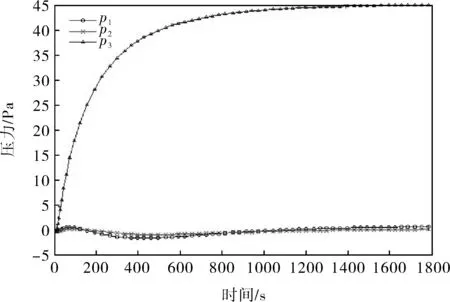
图6 R3=30时的阶跃响应曲线
4 结束语
笔者采用机理建模的方法成功建立了焦炉集气管系的动态数学模型,并通过计算机仿真验证了数学模型的合理性。将智能模糊控制的原理应用于焦炉集气管系的解耦控制,由仿真实验结果可以看出:笔者所建立的智能解耦控制系统基本消除了焦炉集气管系的耦合作用。研究结果能够为焦炉集气管系的解耦控制提供理论依据,可将耦合严重的多回路控制系统视作相互独立的单回路进行控制,为焦炉集气管压力的稳定控制奠定了良好的基础。

