光伏系统MPPT的改进模糊控制

徐晓淳，刘春生，李锋

（南京航空航天大学自动化学院，南京210016）

光伏系统MPPT的改进模糊控制

徐晓淳，刘春生，李锋

（南京航空航天大学自动化学院，南京210016）

为减少光伏系统因外部条件变化而造成的功率损失，减小最大功率点（MPP）处的振荡，并且便于计算机软件实现，采用基于改进模糊控制的最大功率点跟踪（MPPT）技术。在光伏电池工程用数学模型的基础上，分析太阳能发电中的最大功率点原理；在跟踪过程各阶段引入不同的权重，设计了模糊控制规则，并且增加了PI控制环节以改善模糊控制。Matlab/Simulink仿真结果表明，改进的模糊控制光伏系统具有良好的动态性能和稳态性能，在最大功率点处输出功率稳定，提高了能量转化效率。

光伏；改进模糊控制；最大功率点跟踪；数学模型；系统仿真

随着世界能源危机和环境污染问题的日益严重，太阳能光伏发电系统正成为世界关注的热点。我国太阳能辐射既有地域优势又有强度优势，光伏电池发电有着不可比拟的发展前景[1]。光伏系统是非线性的复杂系统，利用智能模糊控制器，针对那些无法获得被控对象清晰的数学模型系统，可以得到较为有效的自动控制方法[2-6]。

本文针对独立型光伏系统，通过对硅太阳能电池的理论数学模型的分析处理，建立一种适用于任意光强和温度的太阳能电池工程简化模型，以更好地实现太阳能光伏发电系统的仿真研究和优化设计。针对光伏电池发电的输出功率低、负载不匹配问题，采用最大功率点跟踪MPPT（maximum power point tracking）技术。在模糊控制自寻优占空比的基础上，改进模糊控制规则，并且增加了PI控制环节，减小其控制系统在最大功率点处的振荡。

1 光伏系统的MPPT原理

为了使光伏电池在不同温度以及光照强度条件下输出尽可能多的功率，在太阳电池与负载之间接入一个阻抗变换器，使得负载的输入阻抗与太阳能电池的输出阻抗总是处于最佳的匹配状态。本文在光伏系统中使用升压变换器（Boost电路）连接光伏电池与负载。该电路输入电流纹波较小，转换效率较高，其阻抗转换关系[5]为

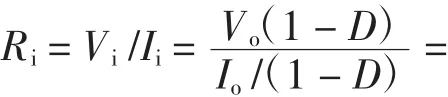
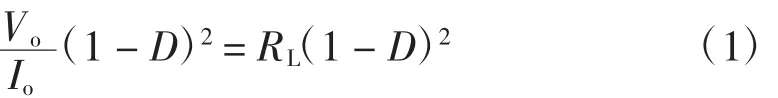
式中：Ri为Boost电路的等效输入阻抗；D为占空比；RL为负载阻抗。在负载不变的情况下，输入阻抗可由D来调节，为系统达到最大功率点创造条件。基于占空比扰动的MPPT方法[7]。其功率与占空比关系如图1所示。当dP/dD=0时，输出功率达到最大。搜索最大功率点的过程为：当上一次占空比的变化使得功率上升时，保持这个变化；当功率下降时，占空比变化方向相反。

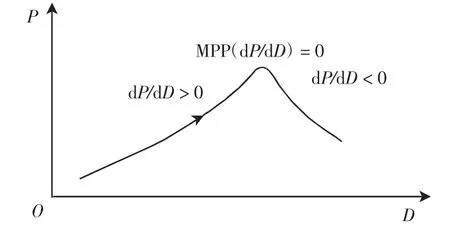
图1 P-D曲线Fig.1P-D curve

2 光伏电池特性

2.1 光伏电池工程用数学模型

光伏电池生产厂家为用户提供标准测试条件下的短路电流（Isc）、开路电压（Voc）、输出最大功率时的电压（Vm）、电流（Im）4个参数，在满足一定精度的情况下使用这些参数建立一个实用的数学模型，光伏电池的I-V方程[8]为

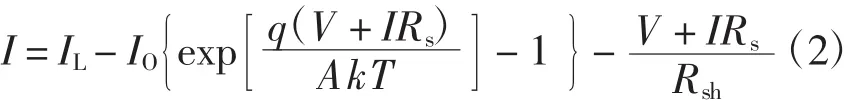
式中：IL为光电流，A；Io为反向饱和电流，A；q为电子电荷常量，1.6×1019C；k为玻耳兹曼常量，1.38× 10-23J/K；T为绝对温度，K；A为二极管因子；Rs为串联电阻，Ω；Rsh为并联电阻，Ω。一般地远小于光电流，此项可以忽略；Rs远小于二极管正向导通电阻，可得IL=Isc。代入最大功率点处参数以及开路状态参数可以解得

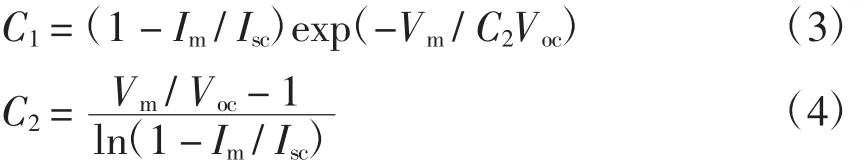
参考标准条件下（tref=298 K，Sref=1 000 W/m2）由I-V特性曲线得到的偏移量为

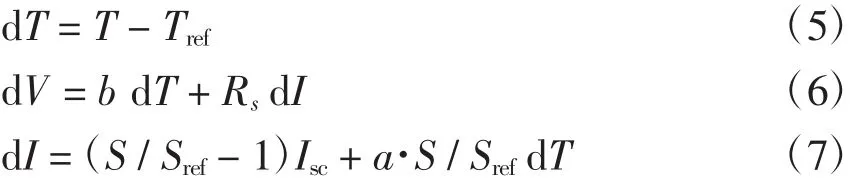
式中，a和b分别为参考日照强度下的电流温度系数和电压温度系数。

由式（2）～式（7）得到新日照强度和电池温度的I-V特性曲线为

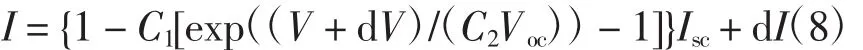
2.2 光伏电池特性曲线

根据式（2）～式（8）建立光伏电池模型，在负载大小连续变化的情况下得到太阳辐射光强变化时光伏电池的输出P-V特性仿真结果，如图2所示。由图2可以看出，随着光照的增强，光伏电池的开路电压减小，最大功率点上移，因此采用MPPT控制追踪最大功率点可以提高能源利用率。

图2 不同光照下光伏电池功率-电压特性曲线Fig.2P-V characteristic curves of PV cells for different intensities

3 光伏系统模糊+PI控制MPPT原理

选取占空比步长作为控制量，根据光伏电池功率的变化量以及前一时刻的占空比步长的变化率决定当前时刻的步长调整量。2个输入变量分别为功率变化量EP和占空比步长变化率CED，即

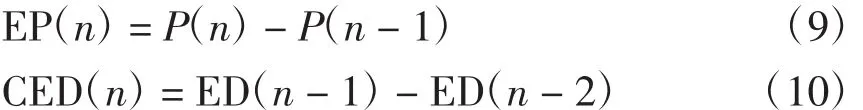
式中：P（n）为n时刻光伏电池输出功率；ED（n-1）为n-1时刻的占空比步长。

引入量化因子GE和GCE，将清晰值从物理论域映射到模糊论域。选定5个模糊子集NB（负大）、NS（负小）、ZZ（零）、PS（正小）、PB（正大），用于涵盖模糊论域EP∈[-5，5]；选定3个模糊子集N（负）、Z（零）、P（正），用于涵盖模糊论域CED∈[-4，4]。所有的模糊子集都选取三角形隶属函数[9]，如图3所示。由于越接近平衡点，功率值变化量越小，因此平衡点附近隶属函数斜率较大，这样分布可以提高控制精度。

引入比例因子KD，将模糊论域映射到物理论域。选定7个模糊子集NB、NM、NS、ZZ、PS、PM、PB，涵盖模糊论域ED∈[-4，4]。

模糊规则的确定是根据操作经验，如果上一次占空比步长的变化使得功率增加，则保持这个变化趋势；反之亦然。这是系统的常规控制[10]。由于特性曲线随着温度及日照强度变化而改变，为了跟随这种环境变化，则增加的模糊规则如下：

if CED is Z and EP is PB（NB），then ED is PM（NM）

if CED is Z and EP is PS（NS），then ED is PS（NS）

在最大功率点的跟踪过程中，由于数模转换离散化引起功率变化为零而未到达最大功率点，实际到达最大功率点时应满足∂P/∂D=0，因此增加的控制规则：

if CED is（PN）and EP is ZZ，then ED is PS（NS）

if CED is Z and EP is ZZ，then ED is ZZ

对于不同的模糊控制规则权重有所区别。常规控制在整个控制过程中占主导地位时，权重设为1.0；环境变化是特殊情况时，权重设为0.5；稳定点是控制的目标点时，权重设为0.25，整个控制过程过渡更加平滑。模糊控制规则如表1所示。

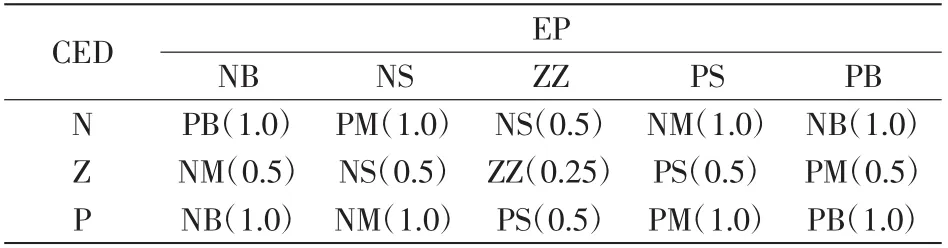
表1 模糊控制规则Tab.1Rule of fuzzy control

模糊控制的输出是占空比步长，即占空比调整量，其作为PI控制器的输入，而PI控制器的输出是ΔD（n）。则DC-DC变换器的占空比D（n）为

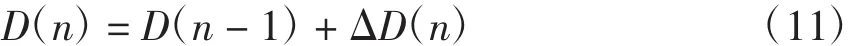
4 基于模糊控制的仿真

通过Matlab/Simulink建立的光伏系统模型如图4所示。太阳能电池模型参数为：标准测试条件下开路电压21.7 V，短路电流4.8 A，最大功率点电压17 V，电流4.4 A，内阻2 Ω，负载电阻10 Ω。电压温度系数0.7 V/℃，电流温度系数0.015 A/℃。利用图形用户界面（GUI）分析和设计模糊推理系统（FIS），模糊推理选用Mamdani型，清晰化方法选用重心法。根据对光伏电池功率的仿真数据，量化因子GE和GCE分别设为1 430、100，比例因子KD设为0.01。PI控制中，比例增益KP设为0.02，积分增益KI设为0.035。

仿真采用ode45解法器，仿真时间设为3 s。光伏电池的表面温度设为25℃，初始光照强度为1 000 W/m2，在1 s时突变为800 W/m2，在2 s时突变为600 W/m2。占空比初值设为0.8，得到的P-V对比曲线、功率变化曲线如图5所示。

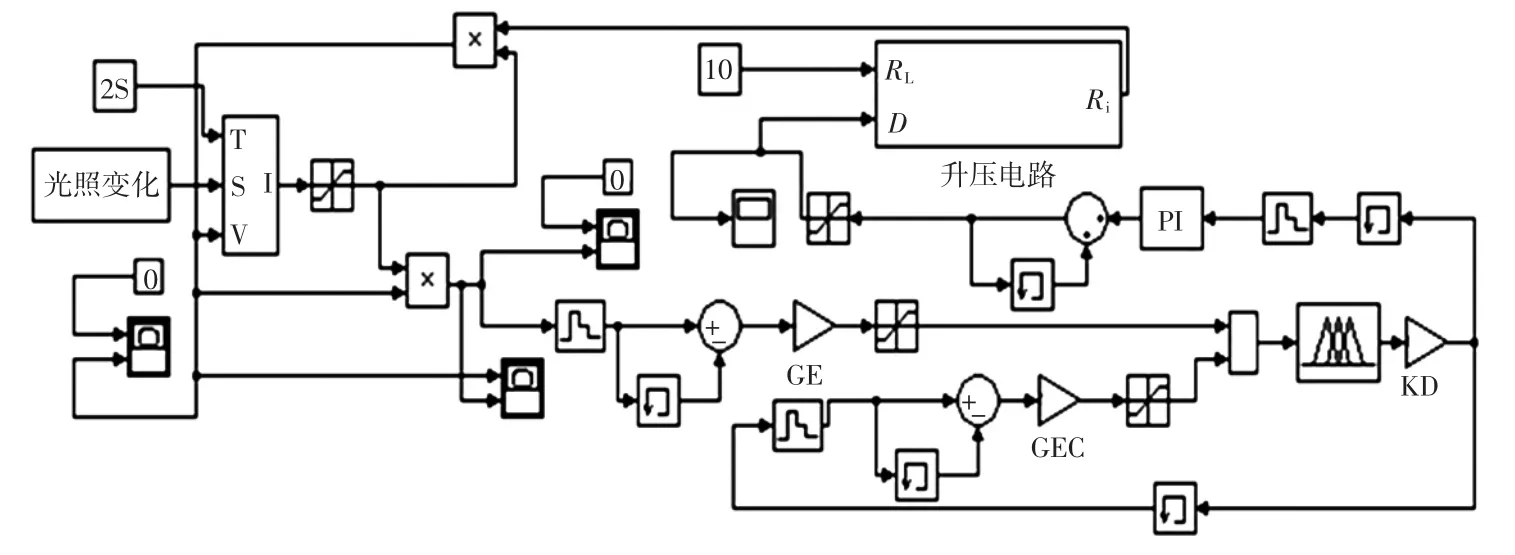
图4 基于改进模糊控制的仿真系统结构Fig.4Structure of simulative system based on the improved fuzzy control

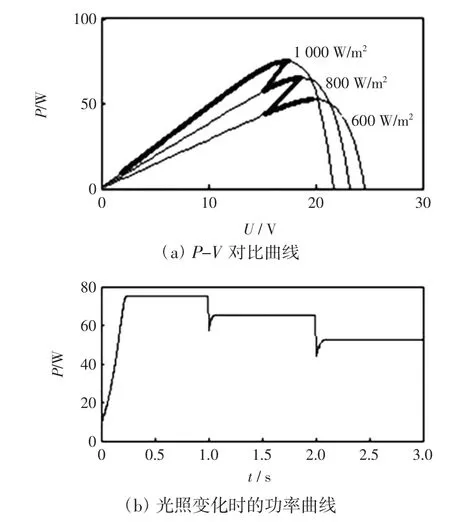
图5 基于改进模糊控制的仿真曲线Fig.5Simulative curves based on improved fuzzy control

由图5可以看出，光照在1 000 W/m2追踪到最大功率点后突变时，功率迅速下降，到达800W/m2后功率增加，之后稳定在最大功率点。经过2次光照的变化，系统都能成功追踪到最大功率点。系统启动时功率迅速上升，到达75 W的调节时间是0.26 s，之后在0.2 s时间内有微小震荡，在0.5 s后输出功率保持在最大功率点。1 s时刻光照突变，在0.1 s的调节时间内，系统追踪到最大功率点，并且功率输出稳定。2 s时刻的变化类似，也能快速追踪到最大功率点。占空比与输出电压相对应，变化特性类似，在较短时间内可以趋于稳定。整个仿真过程显示良好的动态特性与稳态特性。

5 结语

将占空比步长作为控制变量，在传统模糊控制的基础上改进模糊控制规则，并且加入权重，改善了整体的控制效果。在反馈环节中加入PI控制，增加了积分环节，弥补单纯模糊控制只具有微分作用的缺陷，提高了系统的稳定性，对光伏阵列的工程应用有指导作用。与传统的MPPT算法相比，此算法具有编程简单，可离线设计的优点。

[1]李全林.新能源与可再生能源[M].南京：东南大学出版社，2008.

[2]Hu Yufeng，Liu Jun，Liu Bin.A MPPT control msthod of PV system based on fuzzy logic and particle swarm optimization[C]//Second International Conference on Intelligent System Design and Engineering Application.Sanya，China：2012.

[3]Won Chung-Yuen，Kim Duk-Heon，Kim Sei-Chan K，et al.New maximum power point tracker of photovoltaic arrays using fuzzy controller[C]//IEEE Annual Power Electronics Specialists Conference.Taipei，China：1994.

[4]El Khateb A，Rahim N A，Selvaral J.Fuzzy logic controller for MPPT SEPIC converter and PV single-phase inverter [C]//IEEE Symposium on Industrial Electronics and Applications.Langkawi，Malaysia：2011.

[5]Huang Keya，Li Wenshi，Huang Xiaoyang.MPPT of solar energy generating system with fuzzy control and artificial neural network[C]//International Conference Information Technology，Computer Engineering and Management Sciences.Nanjing，China：2011.

[6]Wang Yan，Ding Li，Li Nan.The application of fuzzy parameters self-tuning PID controller in MPPT of photovoltaicpowersystem[C]//InternationalConferenceonTransportation，Mechanical and Electrical Engineering.Changchun，China：2011.

[7]乔兴宏，吴必军，邓赞高，等（Qiao Xinghong，Wu Bijun，Deng Zangao，et al）.模糊/PID双模控制在光伏发电MPPT中应用（MPPT of photovoltaic generation system using fuzzy/PID control）[J].电力自动化设备（Electric Power Automation Equipment），2008，28（10）：92-95.

[8]苏建徽，余世杰，赵为，等（Su Jianhui，Yu Shijie，Zhao Wei，et al）.硅太阳电池工程用数学模型（Investigation on engineering analytical model of silicon solar cells）[J].太阳能学报（Acta Energiae Solaris Sinica），2001，22（4）：409-412.

[9]王传辉，罗耀华（Wang Chuanhui，Luo Yaohua）.太阳能电池最大功率点的模糊控制方法（Fuzzycontrolovermaximum power point tracking of solar cells）[J].应用科技（Applied Science and Technology），2008，35（3）：42-45.

[10]石辛民，郝整清.模糊控制及其Matlab仿真[M].北京：清华大学出版社，2008.

[11]黄舒予，牟龙华，石林（Huang Shuyu，Mu Longhua，Shi Lin）.自适应变步长MPPT算法（Adaptive variable step size MPPT algorithm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：26-30.

Improved Fuzzy Control on MPPT Method of Solar System

XU Xiao-chun，LIU Chun-sheng，LI Feng
（College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Maximum power point tracking（MPPT）based on improved fuzzy control，which is convenient to realize by computer software，is implemented in order to reduce the power loss caused by changeable environment and the oscil lation near the maximum power point（MPP）.The principle of the MPP is analyzed with an engineering mathematic model.The rule of fuzzy control with different weights in the process of tracking is proposed and the PI controller is introduced to improve the fuzzy control.The system simulation result shows that the solar system based on the improved fuzzy control can achieve dynamic and steady-state performance well and produce a more stable power that improved the efficiency of energy conversion.

photovoltaic；improvedfuzzycontrol；maximumpowerpointtracking；mathematicmodel；systemsimulation

TP273.4

A

1003-8930（2014）09-0081-04

徐晓淳（1988—），男，硕士研究生，研究方向为计算机测试与控制。Email：njitxxc@sina.com

2012-08-30；

2012-11-13

刘春生（1955—），女，博士，教授，博士生导师，研究方向为工业自动化。Email：liuchsh@nuaa.edu.cn

李锋（1986—），男，硕士研究生，研究方向为新能源发电与控制技术。Email：lifeng898@163.com