改进的配电网三相潮流计算方法

徐青山，刘中泽，杨永标，李强，辛建波

（1.东南大学电气工程学院，南京210096；2.国电南瑞科技股份有限公司，南京210032；3.江苏省电力公司，南京210024；4.江西省电力公司电力科学研究院，南昌330096）

（4）前推：从首节点到末节点前推计算各节点电压。某支路末节点电压为本支路首节点电压减去本支路压降，即

式中：Um为支路末节点电压；Us为支路首节点电压；Izh为支路电流；Zzh为支路阻抗。

（5）迭代收敛判据：利用计算得到的节点电压和注入电流计算负荷功率，并与初始功率分布相比，若误差小于容许误差，则迭代结束；否者重新迭代计算。

3.2三相牛顿拉夫逊算法

牛顿迭代法是通用的求解非线性方程组方法，应用在潮流计算上称为牛顿拉夫逊法，牛拉法单相和三相拉夫逊潮流计算本质上没有差别，三相牛顿拉夫逊算法求解过程和单相牛拉法是一样的，区别在于牛拉法的三相表现形式，其中最重要的是三相系统的雅可比矩阵求解，类似单相系统雅可比矩阵的推导，可以推导出三相雅可比矩阵。以极坐标形式为例详细推导三相雅可比矩阵。关于三相牛顿拉夫逊算法的具体过程可以参考单相牛顿拉夫逊算法[12]。

根据节点电压法有

节点注入电流为

每个PQ节点a相ΔQ方程为

同理，b、c相也有对应的ΔP、ΔQ方程。

利用ΔP方程对各节点各相θ、U求偏导得矩阵的H、N矩阵各元素；利用ΔQ方程对各节点各相θ、U求偏导得矩阵M、L各元素。

改进的配电网三相潮流计算方法

徐青山1，刘中泽1，杨永标2，李强3，辛建波4

（1.东南大学电气工程学院，南京210096；2.国电南瑞科技股份有限公司，南京210032；3.江苏省电力公司，南京210024；4.江西省电力公司电力科学研究院，南昌330096）

配电网网络参数的不对称使得对称分量法解耦失效，配电网潮流计算元件模型需采用abc全耦合模型。针对配电网长辐射状网络结构可能导致的三相牛顿拉夫逊潮流初值选取难题，提出了一种初值选取方法。首先，将给定的配网三相系统除去合环支路后简化成单相系统，采用单相前推回代得出其潮流解；再利用单相潮流节点电压构造出三相对称电压，以此作为三相牛顿拉夫逊法的初值进行三相潮流计算，克服了配网潮流计算中前推回代与牛顿拉夫逊潮流算法各自的不足。IEEE33节点案例计算结果表明，该方法能够为配电网牛拉法提供合理初值并提高牛拉法收敛速度。

牛顿拉夫逊；前推回代；配电网；潮流计算；三相耦合

随着用户对供电可靠性及电能质量要求的提高，作为电力系统相对薄弱的配电网日益得到重视。配网环网结构、辐射状运行，联络开关经常切换，运行方式多变，潮流计算作为电力系统分析最基本的计算，不仅可以计算网损、校验各种运行方式的合理性等，也可以为暂态计算提供初值，配电网基本潮流计算的重要性不言而喻。

从处理三相的方式[1]上来看，电力系统潮流计算可分为相分量法和序分量法。与输电网不同的是配电网的运行和网络参数不对称，其中网络参数的不对称使得序分量法解耦失效[8]，配电网潮流计算必须基于相分量法，也即考虑全耦合的abc模型。从潮流算法[1-9]上来看，配电网潮流计算应用最多的是前推回代法、牛顿拉夫逊法以及2种算法的改进算法。前推回代法充分利用了配电网辐射状的特点，收敛性好、占用内存少、计算速度快，效率高。但对配网中存在的弱环处理能力弱，需要对配网各节点及支路合理编号，并且对配网中接入的PV以及更多的分布式电源节点处理也十分不便；牛顿迭代法理论上适用于一切非线性方程组的求解、不受环网影响、分布式电源节点处理方便，是通用算法，但也存在对初值敏感、收敛性差、数据存储量大、计算速度慢的缺点，而且配电网多节点、长辐射状，末支路节点电压降落大。传统的牛拉法潮流计算迭代初值平直启动（Vi=1.0 p.u.，θi=0）极易产生初值选取偏离真值太大，导致牛拉法迭代次数多甚至不收敛，为此采用牛拉法进行配网特别是对多节点、长辐射状网络潮流计算时，往往需要解决初值选取问题[10]。

本文采用前推回代为三相牛拉法迭代计算初值，考虑实际配电网环网极少、三相不平衡度低等特点，前推回代潮流采用简化的单相系统计算，简化的单相系统不考虑合环支路，对简化的单相系统进行前推回代潮流计算，利用计算得到的节点电压为牛拉法对称构造出一个较合理三相初值，此初值整体兼顾了配网主辐射结构带来的负荷压降问题，解决了牛拉法的初值选取难题，又减少了牛拉法的迭代次数，提高牛拉法的计算速度，程序的主体仍是通用的牛拉法。

1 三相耦合问题

输电网和配电网都存在着不对称故障现象，配电网存在着网络参数不对称和负荷运行不对称，而输电网如图1所示，不存在这2种不对称现象。图1表示输电或者配电线路，运行上可以表示对称负荷或不对称负荷或不对称故障，后者表现在向网络注入了对称或不对称的电流。

根据互感原理，平行的两根导线通入电流，相互间产生互感，根据无源网络的互感互易性知

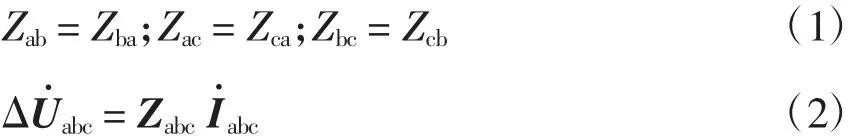
其中

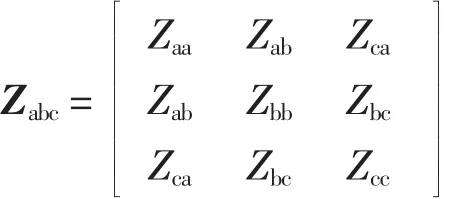
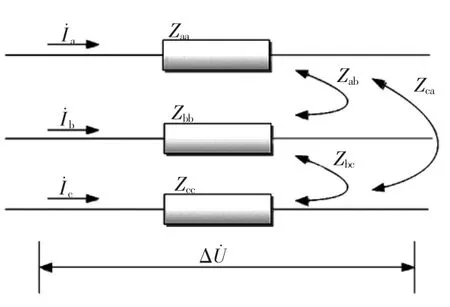
图1 三相耦合Fig.1Three-phase coupling

式（2）表明三相线路各相电流和电压是耦合的，包括对称的输电网也存在耦合问题。而目前处理解耦的方法主要是通过矩阵变换方法进行解耦。三相问题中的矩阵变换解耦常采用的方法是对称分量法，将耦合的相域模型转化为无耦合的序域模型。对称分量法要实现解耦[15]，线路参数必须满足

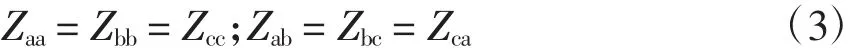
也即网路参数是对称的[17]，否则对称分量法无法实现解耦。输电网满足此条件，可以采用对称分量法解耦；而配电网不满足此条件，不能采用对称分量法实现解耦运算。失效根本原因是配电网网络参数的不对称，对称分量法的解耦失效使得配电网的运算问题更为复杂，表现为节点导纳矩阵、雅可比矩阵阶数是单相或单序计算时的3倍。

本文考虑配网计算的精确性，采用三相abc全耦合模型，考虑存在的所有耦合阻抗，主算法采用三相牛顿拉夫逊潮流算法。

2 改进的配网三相潮流方法

改进的配电网三相潮流方法的计算主体是三相牛顿拉夫逊法，主要体现在采用单相前推回代为三相牛拉法求解迭代初值，计算流程如图2所示，具体步骤如下。

步骤1构建配电网三相系统模型：将配电网上级变电站出口母线视为无穷大电源，并在潮流计算中作为平衡节点，等值为电压幅值和相角为恒定已知量并假定三相电压对称；馈线上所有负荷等效为支路末节点集中负荷，且为恒功率PQ负荷，考虑功率不对称；馈线支路采用集中参数模型，考虑三相之间的耦合电抗。

步骤2配电网节点、支路编号：将平衡节点编号为0，作为根节点，暂不考虑存在的少量合环角，b、c相电压幅值取和a相电压幅值一样大，b相电压相角取a相电压相角减去120°，c相电压相角取a相电压相角加上120°。

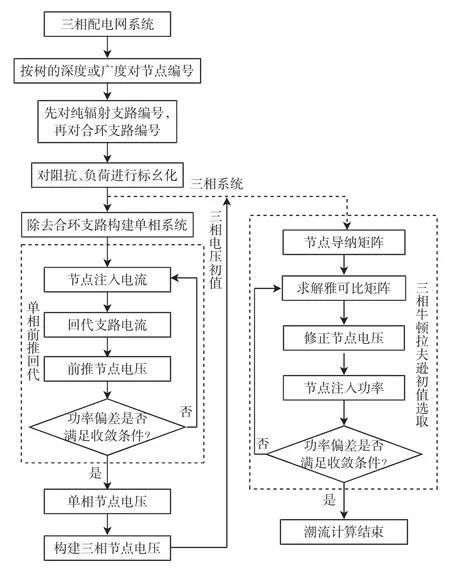
图2 潮流计算流程Fig.2Flow chart of power flow calculation

支路，采用树的广度或深度搜索对配网其他节点进行编号，各支路编号采用支路末节点号，再接着对合环支路编号（顺序无影响）。

步骤3参数标幺化：选取上级变电站母线电压作为基准电压、上级变电站容量为基准功率，将配网中所有线路阻抗、负荷进行标幺化操作。

步骤4单相系统构建：将配网中存在的极少量合环在合环支路处解环，配网呈辐射状，将各辐射支路已经标幺化的a、b、c各相的自阻抗求和后再除以3作为单相系统的对应支路阻抗，所有互阻抗不考虑；将各负荷点已经标幺化的a、b、c各相功率求和后再除以3作为单相系统的对应节点负荷；各节点电压初值为1 p.u.、相角为0，以此方法从全耦合三相系统构建出简化的单相系统。

步骤5单相系统前推回代：单相系统采用前推回代进行潮流计算，由于仅仅是计算牛拉法迭代初值而且前推回代计算效率高、收敛性好，前推回代收敛精度的选择对于最终牛拉法计算精度、运行时间影响甚微，选择范围较宽。

步骤6三相牛顿拉夫逊法初值选取：前推回代求得的单相系统各节点电压幅值、相角作为三相牛顿拉夫逊法的对应节点的a相电压幅值、相

步骤7三相牛顿拉夫逊潮流计算：对步骤1中的三相配电网模型（需要标幺化）采用步骤6中的初值进行三相牛顿拉夫逊法潮流计算，当迭代中所有节点的a、b、c各相有功、无功功率偏差都满足给定精度时，潮流计算结束。

步骤8计算结果：输出潮流计算各节点数据。

综上，本潮流计算方法主要特征有：考虑了实际配网系统存在馈线多、环网极少、各节点电压三相不对称度较低的特点，对构建的无环单相系统影响较小；利用了前推回代计算速度快、收敛好，又避开了前推回代的环网处理难题，为牛拉法提供初值，较少弱环的忽略对合环所在位置局部区域的初值计算有一定的影响，但对弱环外围其他更多节点初值影响甚小；方法的主体仍然是通用的三相牛顿拉夫逊潮流计算。

3 关键步骤

潮流计算方法的核心步骤是单相系统的前推回代计算和三相系统的牛顿拉夫逊计算。

3.1 纯辐射网的前推回代

（1）编号：对纯辐射网的各节点、各支路都按树的广度（或深度）编号，将源节点编号为0，按此编号方式可以得到支路编号等于该支路末节点编号。一种按树的广度编号的拓扑如图3所示。

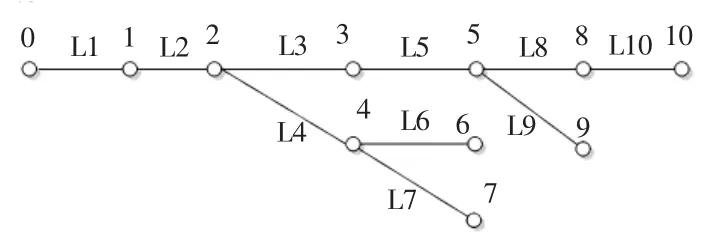
图3 辐射网编号（按树的广度）Fig.3Number of radiation network（by breadth）

（2）注入电流：初始假设所有节点电压幅值为1，相角为0，计算各节点注入电流，如节点k的注入电流为

（3）回代：从末节点到首节点回代计算各支路电流。某支路电流等于该支路所接所有下一支路电流加上本支路末节点注入电流，即

式中：ILk为k支路的支路电流；ILk(i，k)为首末端节点编号为i、x的x支路的支路电流为所有满足首节点编号为k的支路电流求和。

（4）前推：从首节点到末节点前推计算各节点电压。某支路末节点电压为本支路首节点电压减去本支路压降，即

式中：Um为支路末节点电压；Us为支路首节点电压；Izh为支路电流；Zzh为支路阻抗。

（5）迭代收敛判据：利用计算得到的节点电压和注入电流计算负荷功率，并与初始功率分布相比，若误差小于容许误差，则迭代结束；否者重新迭代计算。

3.2三相牛顿拉夫逊算法

牛顿迭代法是通用的求解非线性方程组方法，应用在潮流计算上称为牛顿拉夫逊法，牛拉法单相和三相拉夫逊潮流计算本质上没有差别，三相牛顿拉夫逊算法求解过程和单相牛拉法是一样的，区别在于牛拉法的三相表现形式，其中最重要的是三相系统的雅可比矩阵求解，类似单相系统雅可比矩阵的推导，可以推导出三相雅可比矩阵。以极坐标形式为例详细推导三相雅可比矩阵。关于三相牛顿拉夫逊算法的具体过程可以参考单相牛顿拉夫逊算法[12]。

根据节点电压法有

节点注入电流为

其中：

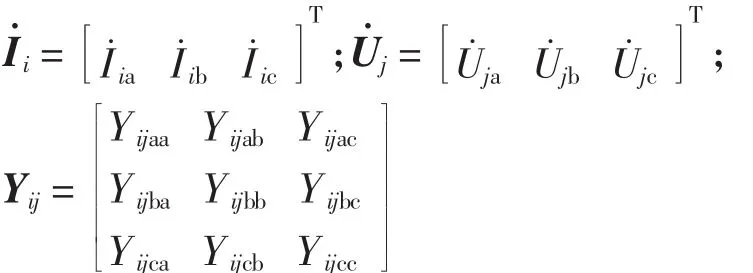
则

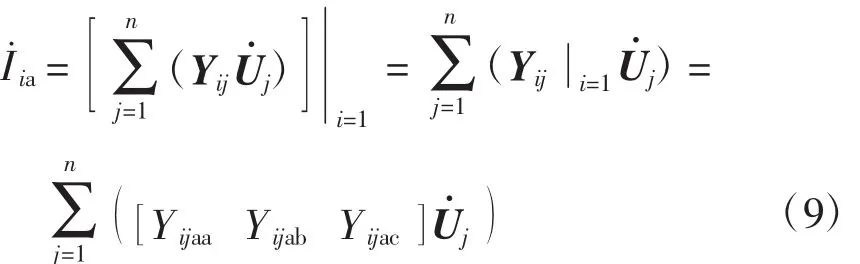
而

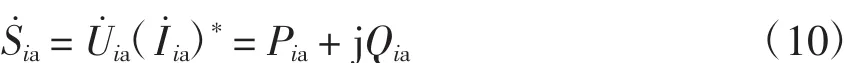
得

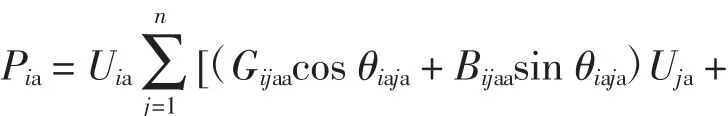
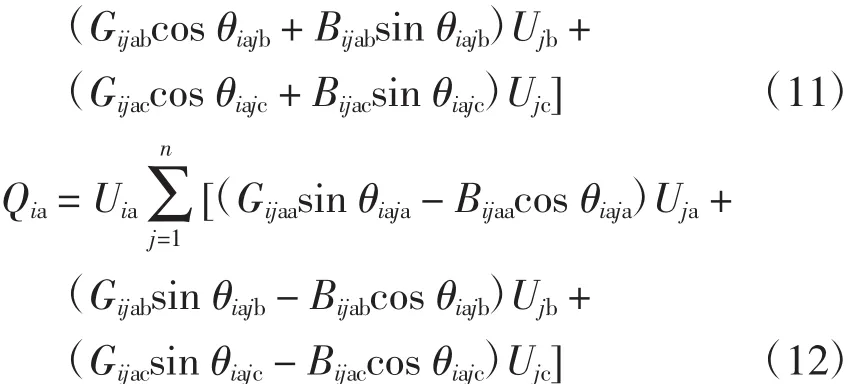
单相极坐标雅可比矩阵形式为

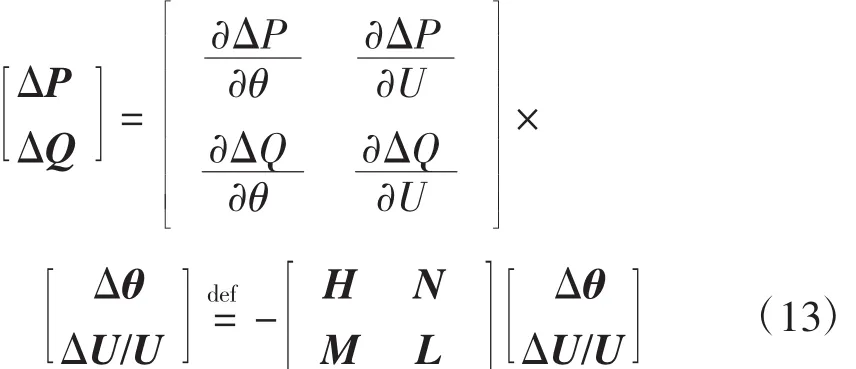
三相雅可比矩阵形式上与单相一样，只是单相公式中各向量中每个元素是3×1列向量、雅可比矩阵中的每个元素是3×3矩阵，如

每个PV、PQ节点a相ΔP方程为

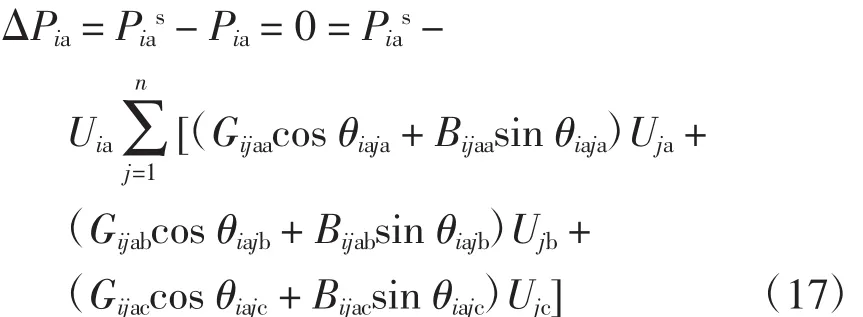
每个PQ节点a相ΔQ方程为

同理，b、c相也有对应的ΔP、ΔQ方程。

利用ΔP方程对各节点各相θ、U求偏导得矩阵的H、N矩阵各元素；利用ΔQ方程对各节点各相θ、U求偏导得矩阵M、L各元素。

a相ΔP方程对θ求偏导后对应的矩阵H的各元素求解结果为

当i≠j时，

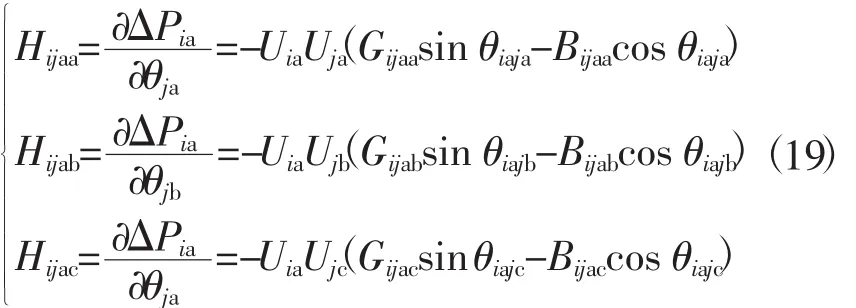
当i=j时，

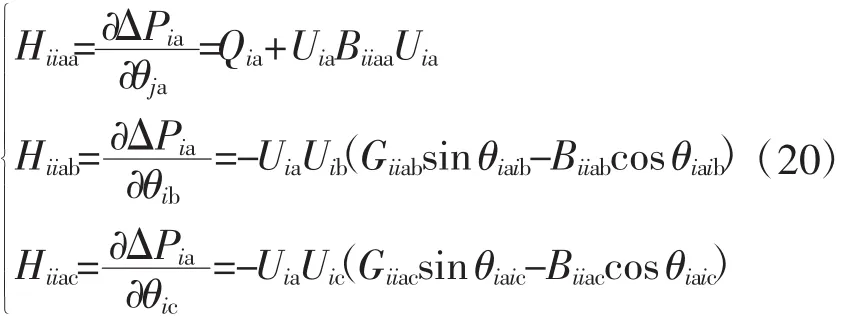
对比单相牛拉法雅可比矩阵公式，可以发现，推导出的三相雅可比矩阵公式与单相公式相似。由此可见，牛拉法三相雅可比矩阵与单相雅可比矩阵不仅形式一致，而且结果一致。

a相功率不平衡方程对应的矩阵N、矩阵M、矩阵L的各元素可以类似求偏导求解。对于雅可比矩阵中的与b、c相功率不平衡方程相关的元素可以采用类似a相的方法推导，也可以根据a、b、c下标之间的对称性，直接写出结果。

4 案例测试

选取IEEE33节点测试系统，网络拓扑及编号如图4所示。图中节点及支路按树的深度编号，节点初始数据参考文献[14]，取UB=12.67 kV，SB=10 MVA。考虑前推回代算法仅仅是为牛拉法计算初值而且效率较高，选取收敛精度较高会影响程序的最终运行时间，选取较低会影响牛拉法的收敛性，此处选为0.000 1，三相牛拉法收敛精度选为0.000 000 1。为说明弱环对三相牛拉法的影响情况，构建测试案例，如表1所示，潮流程序计算迭代结果如表2所示，案例1（有初值计算）的潮流后各节点电压表3所示。

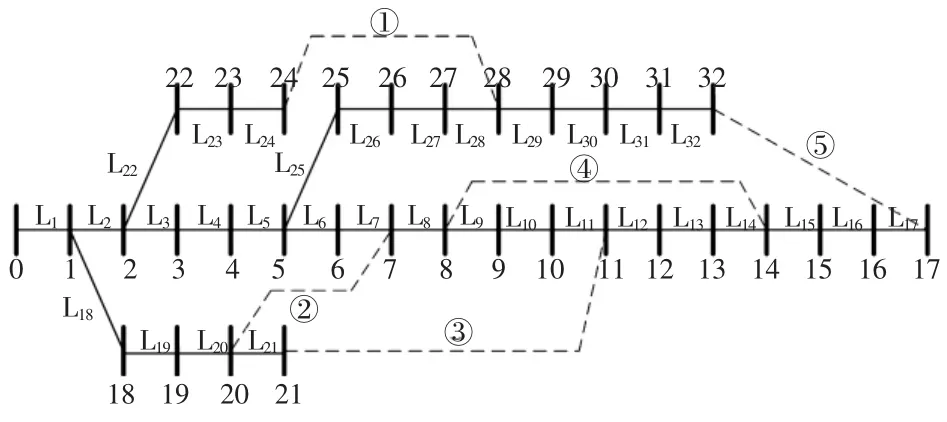
图4 IEEE33节点Fig.4Topology of IEEE33

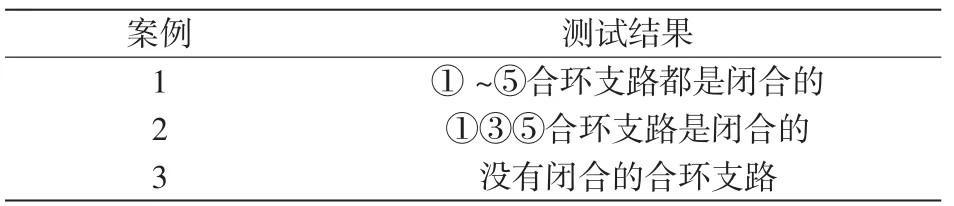
表1 测试案例Tab.1Test case

表2 三相牛拉法的迭代信息Tab.2Iteration information of three-phase Newton-Raphson

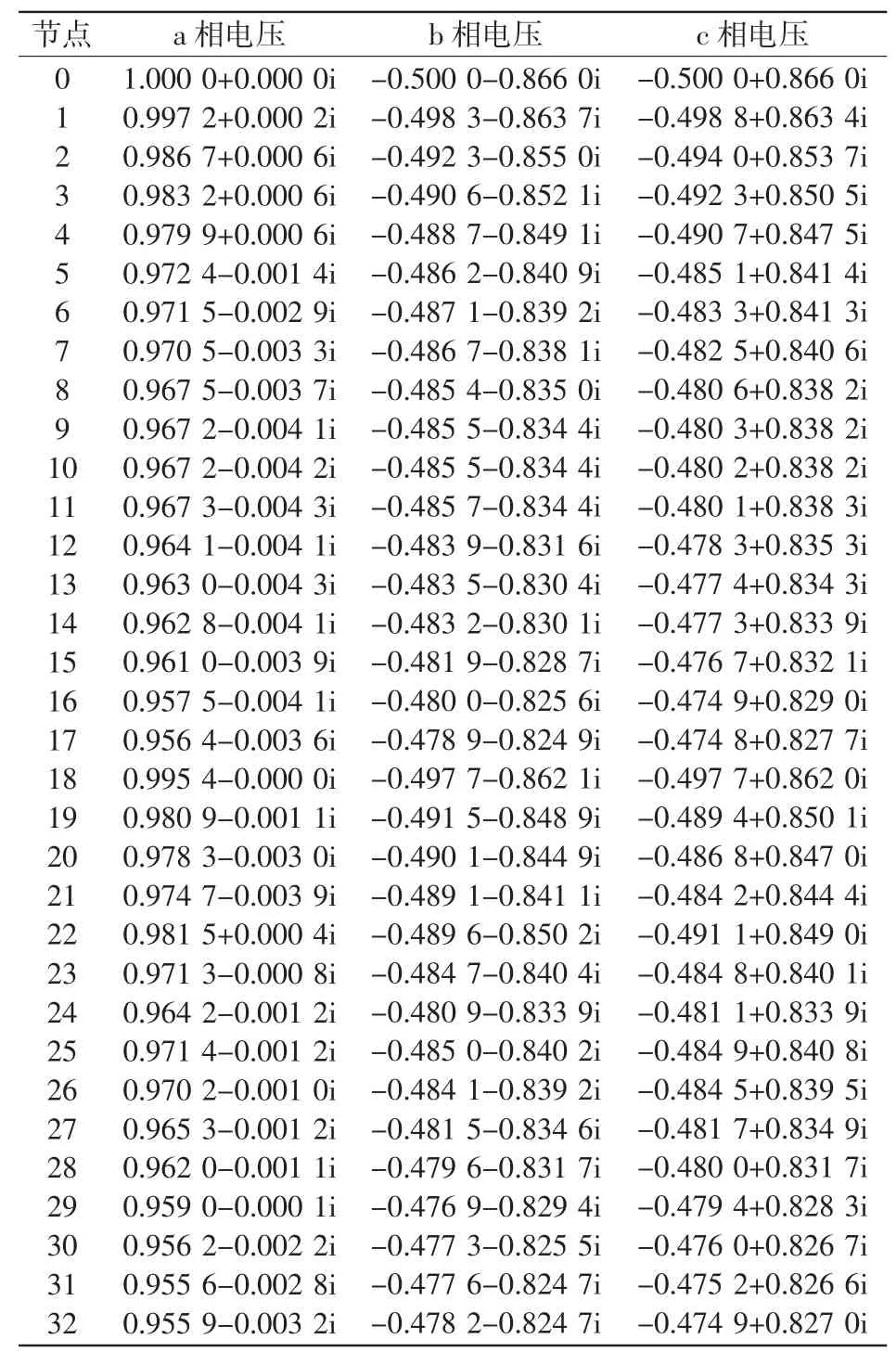
表3 案例1（有初值计算）的计算结果Tab.3Calculation results of case 1（with initial value）

从案例1的2种计算方法可以判断出采用前推回代为牛拉法提供初值计算可以提高牛拉法的收敛速度；案例3是纯辐射网，牛顿迭代次数最少，表明对于配电网环网越少，前推回代（不考虑环）计算出的初值越接近迭代真值，从而牛顿迭代次数越少。由此可见弱环的忽略对初值有所影响，表现在环较多案例牛拉法迭代次数要大于或等于环较少案例牛拉法迭代次数，但采用前推回代初值计算比没有初值计算的牛拉法潮流计算迭代次数更少，故本文所提方法是有效的，而且环越少，效果越明显。

5 结语

本文提出的配电网三相潮流计算方法具有简单、实用、效率高等特点，潮流计算的核心是abc三相模型下的牛顿迭代算法，能够处理由于三相参数不对称和三相负荷不对称带来的全耦合问题；采用不考虑弱环的纯辐射网前推回代法能够高效的为牛拉法计算出合适初值，不仅能解决辐射网中牛拉法初值难题，而且能提高牛拉法的收敛速度。此外牛拉法兼顾弱环，能精确计算出配网潮流真值，能够适应大规模配网络结构特点的要求。不足的是，本文探讨的主要是常见的普通配电网，并没有对配网中存在的PV节点以及更多的分布式电源节点处理进行研究。

测试案例表明了本文提出的方法可以解决牛拉法的收敛速度，但由于节点数过少，辐射线路太短，加上没有重负荷现象，以致IEEE33节点系统直接采用三相牛拉法也不会出现由于平直启动初值不当导致的不收敛问题。而实际配电网对于33个节点存在5个环，环的个数偏多，实际的配网也远不止33个节点，可以预知对于含弱环配网，采用单相前推回代法可以为三相牛拉法潮流计算提供初值，提高牛拉法收敛速度，并且是环的比例越低、节点数越多、辐射线路越长、负荷越重，本方法优势越明显。此外对于负荷严重不对称导致三相节点电压不对称严重的配电网系统，可以将本方法中的单相前推回代改进为三相前推回代，以提高三相牛拉法的初值精度。

[1]王守相，李继平，王成山，等（Wang Shouxiang，Li Jiping，Wang Chengshan，et al）.配电网三相潮流算法比较研究（Comparison and research on three-phase power flow methods for distribution systems）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2000，12（2）：26-31.

[2]Dukpa A，Venkatesh B，El-Hawary M.Application of continuation power flow method in radial distribution systems[J].Electric Power Systems Research，2009，79（11）：1503-1510．

[3]Chang G W，Chu S Y，Wang H L.An improved backward/ forward sweep load flow algorithm for radial distribution systems[J]．IEEE Trans on Power Systems，2007，22（2）：882-884．

[4]刘雅静，杨明皓（Liu Yajing，Yang Minghao）.配电网三相潮流计算（Three-phase power flow for distribution system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2002，14（1）：59-63.

[5]Sameni A，Nassif A B，Opathella C，et al.A modified Newton-Raphson method for unbalanced distribution systems[C]//IEEE International Conference on Smart Grid Engineering.Oshawa，Canada：2012.

[6]索南加乐，单亚洲，李怀强，等（Suonan Jiale，Shan Yazhou，Li Huaiqiang，et al）.配网三相潮流的常雅可比牛顿算法（A novel three phase load flow algorithm with constant Jacobian matrix for distribution system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2004，16（1）：14-18.

[7]张勤，周步祥，林楠，等（Zhang Qin，Zhou Buxiang，Lin Nan，et al）.基于Zbus和前推回代法的配电网潮流计算（Improved power flow algorithm for distribution networks based on Zbus algorithm and forward/backward sweep method）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（6）：73-77.

[8]姜彤，郭志忠，陈学允，等（Jiang Tong，Guo Zhizhong，Chen Xueyun，et al）.多态相分量法及其在电力系统三相不对称分析中的应用（Polymorphic phase components method and its application in three-phase unbalance calculation of power system）[J].中国电机工程学报（Proceedings of the CSEE），2002，22（5）：70-74.

[9]赵晶晶，李新，许中（Zhao Jingjing，Li Xin，Xu Zhong）.含分布式电源的三相不平衡配电网潮流计算（Calculation of three-phase unbalanced power flow in distribution network containing distributed generation）[J].电网技术（Power System Technology），2009，33（3）：94-98.

[10]梅贱生，陈恳（Mei Jiansheng，Chen Ken）.潮流计算的初值选择对其收敛性影响的探讨（The research for the influence of the choice of initial value in power flow′s calculation for its convergence）[J].南昌大学学报：理科版（Journal of Nanchang University：Natural Science），2007，31（专辑）：154-156，160.

[11]Hocaoglu M H，Eminoglu U．A new power flow method for radial distribution systems including voltage dependent load models[J]．Electric Power System Research，2005，76（1-3）：106-114．

[12]单渊达.电能系统基础[M].北京：机械工业出版社，2003.

[13]车仁飞，李仁俊，白树忠（Che Renfei，Li Renjun，Bai Shuzhong）.配电网络拓扑分析与三相潮流计算的实现（Implementation of topology analysis and three-phase power flow for distribution systems）[J].继电器（Relay），2003，31（3）：33-36.

[14]车仁飞，李仁俊（Che Renfei，Li Renjun）．一种少环配电网三相潮流计算新方法（A new three-phase power flow method for weakly meshed distribution systems）[J]．中国电机工程学报（Proceedings of the CSEE），2003，23（1）：74-79.

[15]王一宇，周与邦.电力系统暂态[M].北京：中国电力出版社，2003.

[16]王守相，黄丽娟，王成山，等（Wang Shouxiang，Huang Lijuan，Wang Chengshan，et al）.分布式发电系统的不平衡三相潮流计算（Unbalanced three-phase power flow calculation for distributed power generation system）[J].电力自动化设备（Electric Power Automation Equipment），2007，27（8）：11-15.

[17]Tang Xiaobo，Tang Guoqing．Multi-objective planning for distributed generation in distribution network[C]//Third IEEE International Conference on Electric Unity Deregulation.Nanjing，China：2008．

[18]唐小波，徐青山，唐国庆（Tang Xiaobo，Xu Qingshan，Tang Guoqing）.含分布式电源的配网潮流算法（Power flow algorithm for distribution network with distributed generation）[J].电力自动化设备（Electric Power Automation Equipment），2010，30（5）：34-37.

[19]Wang Jincheng，Chiang Hsiao-dong，Darling G R.An efficient algorithm for real-time network reconfiguration in large scale unbalanced distribution systems[C]//Power Industry Computer Application Conference.Salt Lake City，USA：1995.

Improved Method of Distribution Network Three-phase Power Flow Calculation

XU Qing-shan1，LIU Zhong-ze1，YANG Yong-biao2，LI Qiang3，XIN Jian-bo4
（1.School of Electrical Engineering，Southeast University，Nanjing 210096，China；2.NARI Technology Development Co.，Ltd.，Nanjing 210032，China；3.Jiangsu Province Electric Power Company，Nanjing 210024，China；4.Jiangxi Province Electric Power Research Institute，Nanchang 330096，China）

The asymmetry of network parameters makes the symmetrical component method failing in three-phase decoupling，and the distribution network elements'modeling should use abc coordinate full coupling for accurate result. Considering the probable initial value selection problem of Newton method due to long radial network，one selection method is propesed.First，for a given three-phase distribution network，the loop closing branches are remored and the three-phase system is simplified to a single-phase system，and single phase forward-backward algorithm is used to calculate the single phase system.Then the single-phase calculation node voltage is used to construct a positive sequence three-phase node voltage as the initial value of three-phase Newton-Raphson power flow calculation.The method overcomes the deficiency of both the forward-backward algorithm and Newton power flow algorithm.IEEE33 node case shows that this method can solve Newton algorithm initial value selection problem in radiation network and can improve its convergence speed.

Newton-Raphson；forward-backward；distribution network；power flow calculation；three-phase coupling

TM744

A

1003-8930（2014）09-0023-07

徐青山（1979—），男，博士，教授，博士生导师，研究方向为新能源发电及微电网运行与控制。Email：xuqingshan@seu. edu.cn

2013-10-10；

2013-12-09

江苏省自然科学基金项目（BK2012753）；国家电网公司科技项目（52182013000V）；江苏省电力公司科技项目资助项目（J2013073）；国家电网公司科技项目“智能配用电的技术体系及仿真基础性问题研究”；国家自然科学基金资助项目（51377021）

刘中泽（1989—），男，硕士研究生，研究方向为配电网的稳态与暂态研究。Email：ahliuzhongze@126.com

杨永标（1978—），男，硕士，工程师，研究方向为配电和用电研究。Email：yanggyongbiao@sgepri.sgcc.com.cn