分布式电源并网逆变器谐波抑制方法

韩莹，陈维荣，李奇，刘志祥

（西南交通大学电气工程学院，成都610031）

1.图要精选，应具有自明性，切忌与表及文字表述重复。

2.图要精心设计和绘制，要大小适中，线条均匀，主辅线分明。

3.坐标图标目中的量和单位符号应齐全，并分别置于纵、横坐标轴的外侧。

4.图中的术语、符号、单位等应与表格及文字表述所用的一致。

分布式电源并网逆变器谐波抑制方法

韩莹，陈维荣，李奇，刘志祥

（西南交通大学电气工程学院，成都610031）

为了解决传统的比例-积分（PI）控制器由于自身缺陷引起的电压、电流谐波问题，提出了两相同步旋转坐标系下基于比例-积分-谐振（PIR）控制器的电压、电流双闭环逆变器控制策略；同时引入了简化三电平空间矢量脉宽调制（SVPWM）算法，并在此基础上提出相电压重构方法。仿真实验表明，上述控制策略对指定次谐波具有良好的抑制效果，采用该策略的逆变器具有良好的输出特性，进而验证了该控制策略对并网系统的有效性。

并网逆变器；比例-积分-谐振控制器；三电平空间矢量脉宽调制；相电压重构；总谐波畸变率

近年来，随着能源危机和环境问题日益严峻，含有风力发电、光伏发电及燃料电池等分布式电源的发电系统因其灵活可靠、安全稳定、绿色环保等优点受到了广泛关注[1-3]。在分布式发电系统中，并网逆变器作为实现电能馈送电网的重要环节，直接影响到分布式发电系统的整体性能。因此，并网逆变器的控制方法成为国内外分布式发电领域研究的热点问题[3-4]。

基于dq变换坐标系下的前馈解耦PQ控制是目前分布式电源并网逆变器控制的主流控制策略之一，通过跟随电网电压，控制注入电流进而调节输出功率，其实质是将有功功率和无功功率解耦后分别控制[4-6]。在传统的PQ控制方法中，一般采用电压、电流双闭环控制策略，其电流内环一般引入网压前馈PI控制器。在传统的分布式发电系统中，系统含有的低次谐波严重影响了并网逆变器的输出电流质量。但在dq坐标系下，PI控制器因自身的缺陷只能实现直流信号的无静差控制，对于系统谐波引起的交流分量难以实现无静差控制，使得逆变器输出一定的低次谐波[6]。

为了解决分布式发电系统的谐波问题，文献[7]采用基于正负零序分量分解的逆变器控制策略实现对正序、负序和零序分量的独立控制；文献[8]提出基于重复PI控制的逆变器控制策略以抑制输出电流的周期性扰动；文献[9]提出基于虚拟磁链的矢量控制策略实现对谐波的抑制，虽然上述方法对谐波有一定的抑制效果，但是其动态效果差，算法复杂，极大地限制了其应用场合；文献[10]提出同步旋转坐标系下的PR控制器实现了对谐波信号的无静差控制，以改善控制系统的性能。但其只在基波和指定谐波附近具有较大增益，对于低频扰动的抑制能力很差，难以对并网电流中的直流分量进行有效控制。

本文结合比例-积分-谐振（PIR）控制器和基于电压矢量重构策略的简化三电平SVPWM算法的优点，将两者应用于传统的电压、电流双闭环PQ控制策略中以实现对并网逆变器输出电能质量的有效控制。在此基础上建立50 kW分布式电源并网系统仿真模型，仿真结果验证了该并网逆变器控制策略的正确性和有效性。

1 分布式电源并网系统

图1为微电源并网系统结构。在分布式电源并网系统中，整流后的分布式电源DG经过DC/AC逆变器和LC滤波器完成从直流到交流的转换，进而实现将分布式电源提供的直流转换成与电网系统和负荷设备标准相匹配的电压和频率。

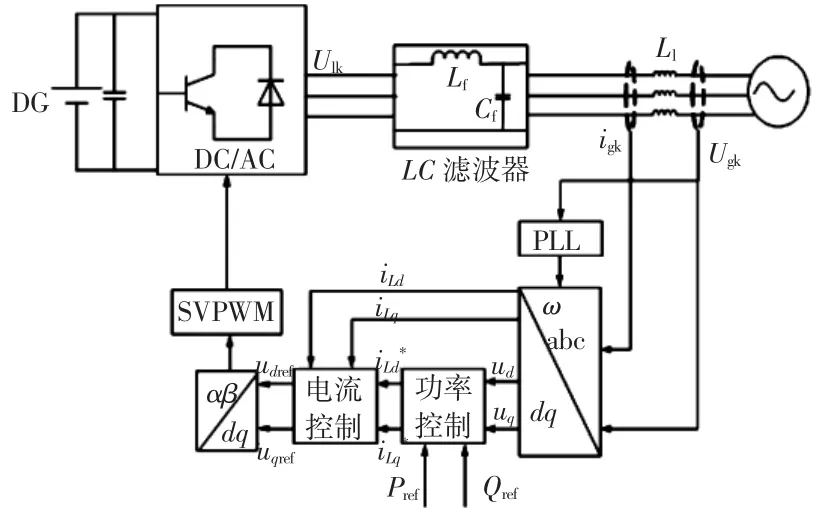
图1 并网系统控制结构Fig.1Structure of grid-connected control system

图中，DG为由经整流后的分布式电源；Lf和Cf分别为滤波器的滤波电感和滤波电容；Ll为线路电感；Ulk为逆变器滤波前输出的线路电压；Ugk为配电网电压，即

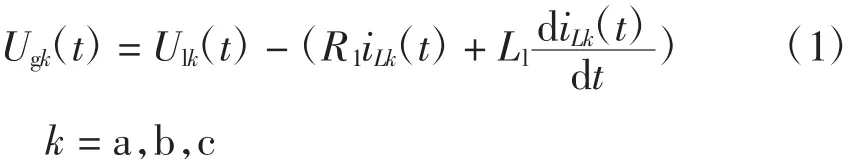
将式（1）从abc坐标系转换为dq坐标系，则

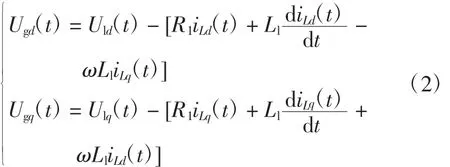
逆变器输出功率为

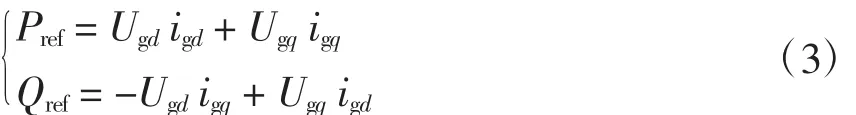
在电网正常情况下，d轴电压Ugd=Um，q轴电压Ugq=0。则逆变器输出功率为

内环电流参考值为

Um在dq坐标系下定义为

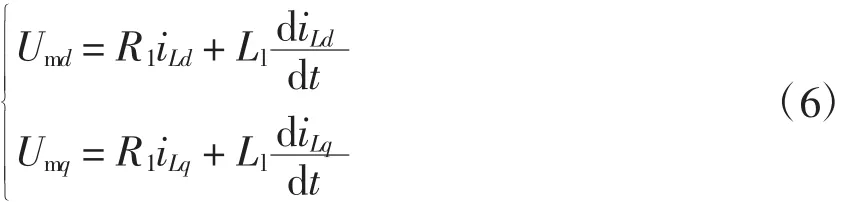
将式（6）带入式（2）得

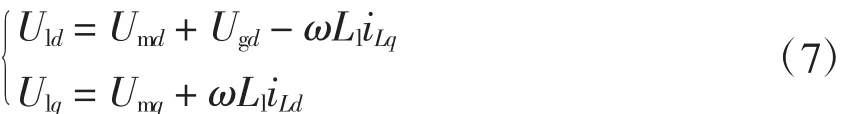
根据式（5）和式（7）设计的PQ控制器见图2。

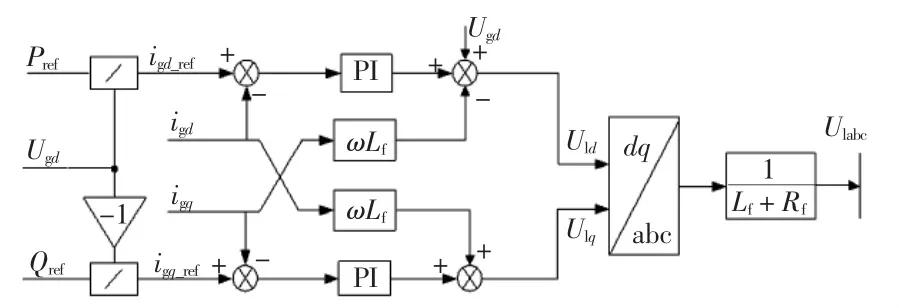
图2 PQ控制器框图Fig.2Block diagram of PQ controller

由图2可知，在dq坐标系下通过有功参考量Pref和无功参考量Qref计算得出电流参考量igd_ref和igq_ref。其值与实际测量得到的电流信号igd和igq作差后经过PI控制器调节后得到dq坐标系下电压参考信号U′ld以及U′lq。同时，考虑线路电感的耦合影响，引进了电流状态反馈-ωLiLd和-ωLi′Lq，进而得出dq坐标系下逆变器输出的电压分量Uld和Ulq。最后，通过Park反变换得到驱动SVPWM的三相控制分量对逆变器的控制。

2 简化三电平SVPWM算法及相电压重构

三电平SVPWM并网逆变器具有直流电压利用率高、电网电流总谐波畸变率THD（total har－monic distortion）低、输出电压变化率相对较低、电磁干扰小、算法简单、适合数字化等方面的优点，广泛应用于大功率逆变电路中。传统的三电平SVPWM算法将整个矢量空间分成6个大区域，再将每个大区域细分成6个小区域，分别求出参考电压在每个小区域中各个有效矢量作用时间，即对36个小区域分别进行求解，计算繁琐，难以通过软件实现[11-13]。三电平电压空间矢量调制简化算法如图3所示，通过电压坐标平移即可将传统的三电平SVPWM空间矢量图分解为6个两电平SVPWM空间矢量图，将复杂的三电平SVPWM算法计算转化为较为成熟的两电平SVPWM算法。

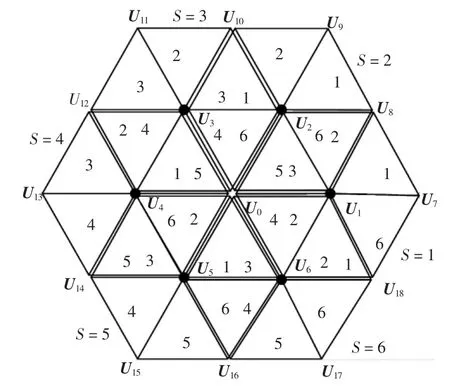
图3 三电平电压空间矢量调制简化算法Fig.3Simplified algorithm of three-level SVPWM

以扇区1为例，参考电压空间矢量的修正如图4所示。参考电压空间矢量修正量Uref′等于参考电压矢量Uref减去扇区1所对应的小矢量U1，再分解至αβ两相静止坐标系，即：Uref_α′=Uref_α-1/3Udc；Uref_β′=Uref_β。各扇区电压矢量修正如表1所示。

根据修正后的参考电压矢量Uref_α′和Uref_β′，利用两电平SVPWM算法可方便地计算电压矢量作用时间，然后根据SVPWM 7段式组合原则完成对各个基本矢量对应的开关状态和作用次序的确定，最终达到简化三电平SVPWM计算的作用[13]。

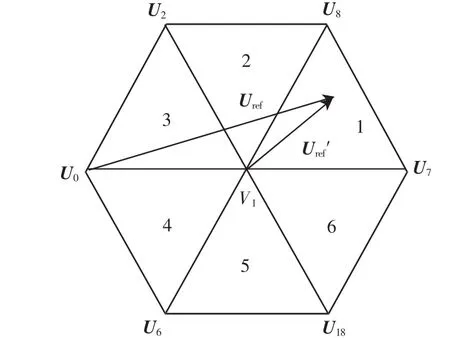
图4 电压矢量修正图Fig.4Correction diagram of voltage vector

表1 电压矢量修正表Tab.1Correction table of voltage vector

3 PIR电流调节器

3.1 PIR控制器的基本原理

PIR控制器是在PI控制器的基础上引入谐振控制器以提高在指定谐振点的增益，提高逆变器输出电能质量。谐振控制器通过产生一个给定信号的极点，实现对该信号的增益无穷大，从而达到逆变器闭环无静差控制的目的[12-14]。理想的谐振控制器传递函数为

式中：n为谐波次数；ω0为基波频率。

理想的谐振控制器相当于谐振频率为nω0的积分器，在谐振点nω0处增益无穷大，且在谐振点两侧增益急剧下降。在实际应用中，理想谐振控制器无法实现。在理想振控制器中加入衰减项2ωcs（ωc为截止频率），增加谐振部分在谐振频率点的增益带宽，以增强谐振部分对电网频率偏移的鲁棒性，进而提高系统的稳定性。改进后的谐振控制器传递函数为

谐振控制器与传统的PI控制器相结合构成PIR控制器，不仅具有PI控制器良好的稳态性能，还兼具谐振控制器的动态性能。PIR控制器的传递函数为

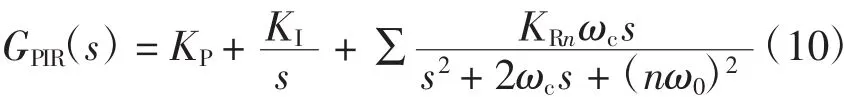
式中：KP为比例系数；KI为积分系数；KRn为n次谐波谐振增益系数。

3.2 PIR电流调节器设计

传统的PI电流控制器由于带宽限制难以实现对逆变器输出电流中大量的5、7、11和13次谐波分量的有效控制。将PIR电流调节器引入分布式电源并网系统中，从而提高在控制器谐振点处的系统增益，以改善并网逆变器的输出性能。在基波正序同步旋转坐标系下，逆变器输出电流的基频正序、5、7、11、13次谐波分量可分别转换成直流分量、6倍频分量和12倍频分量。对于直流分量可利用PIR电流调节器中的PI控制器部分进行无静差控制，而通过PIR电流调节器中的6倍频和12倍频谐振控制器可以实现对6倍频分量和12倍频分量的有效控制，则PIR电流调节器的传递函数为

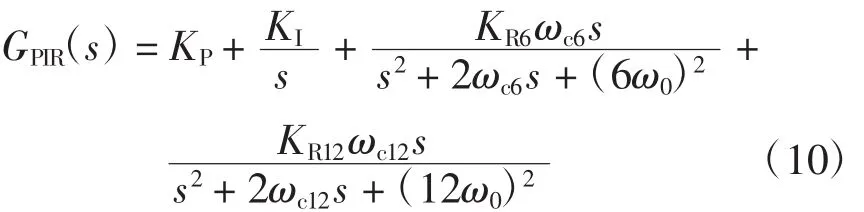
利用双线性变换法离散为

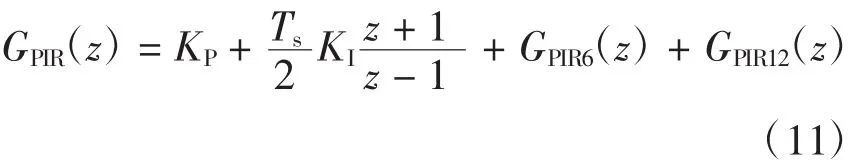
其中：

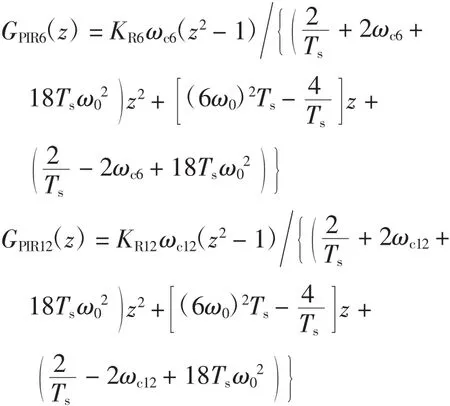
3.3 控制器性能分析

PIR控制器以及传统PI控制器的幅频和相频特性如图5所示，其中在PIR控制器中：KP=2.5，KI=10，KR6=KR12=25，ωc6=ωc12=5；在PI控制器中：KP=2.5，KI=10。由图5可以看出，PIR控制器相对于传统的PI控制器能够有效地增加其在6倍频和12倍频谐振点处的增益，提高了系统对谐波的控制性能。

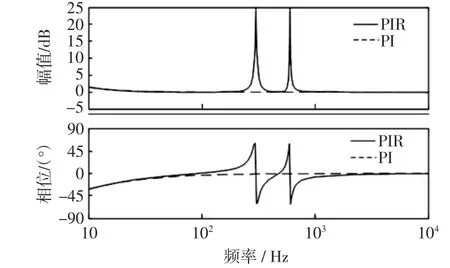
图5 PI和PIR控制器波特图Fig.5Bode diagram of PI and PIR controllers

基于PIR调节器的电流闭环控制框图如图6所示。图中：GPIR（s）为PIR电流调节器的传递函数；Gd（s）和Gf（s）分别为逆变器和LC滤波器的传递函数，则逆变系统的闭环传递函数为

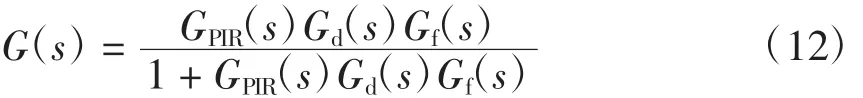
其中：

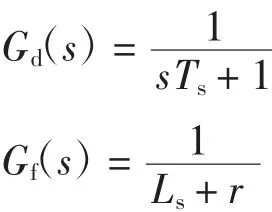
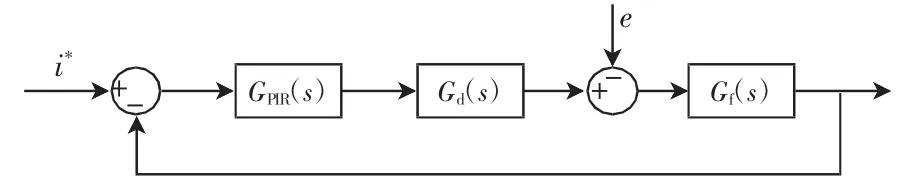
图6 系统的电流闭环控制框图Fig.6Block diagram of current closed-loop control system

图7 为基于PI控制器和PIR控制器的并网系统闭环波特图比较，其中逆变器采样频率Ts= 1/8 000 s，LC滤波器参数为：L=1 mH，R=0.004 Ω，C=50 μF。由图7可以看出，PIR控制器能够增加谐振点增益，提高系统稳定性。

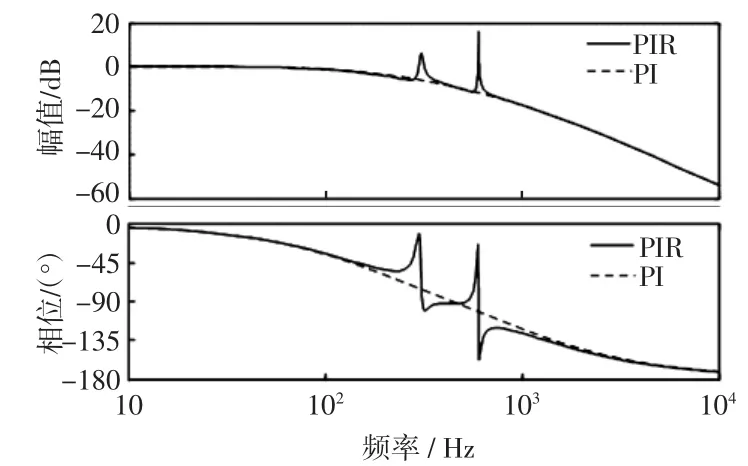
图7 PI和PIR电流调节器闭环波特图Fig.7Closed-loop Bode diagram of PIR and PI current controllers

4 仿真验证

在Matlab/Simulink中搭建基于PIR控制器的三电平并网逆变器控制系统模型。系统仿真参数如下：直流母线参考电压为1 000 V，三相电网线电压380 V，滤波电感为1 mH，滤波电阻为0.004 Ω，滤波电容为50 μF，低压配电网容量为380 V/40 MVA，本地负载为1 MW。

图8和图9分别为采用传统的PI电流调节器和PIR电流调节器的仿真结果及其傅里叶分析。由图8可以看出，采用传统的PI电流调节器逆变器输出电流含有大量（6n±1）次谐波分量，特别是5、7、11和13次谐波含量较大，分别为3.2%、1.7%、1.2%和1.9%，输出电流THD为4.15%，电流畸变较为明显。采用PIR电流调节器后，仿真结果如图9所示，逆变器输出效果具有明显改善，能够较好抑制5、7、11和13次谐波分量，谐波含量分别为0.26%、0.24%、0.12%和0.08%，输出电流总谐波畸变率为1.44%，满足分布式电源并网要求。

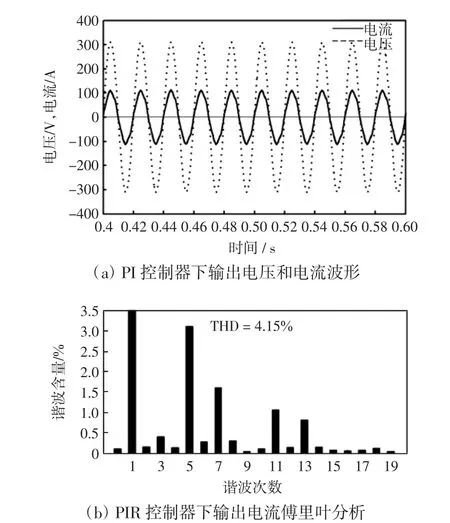
图8 PI控制器的逆变器仿真结果及输出电流傅里叶分析Fig.8Simulation results of grid-connected inverter and Fourier analysis of output current based on PI controller

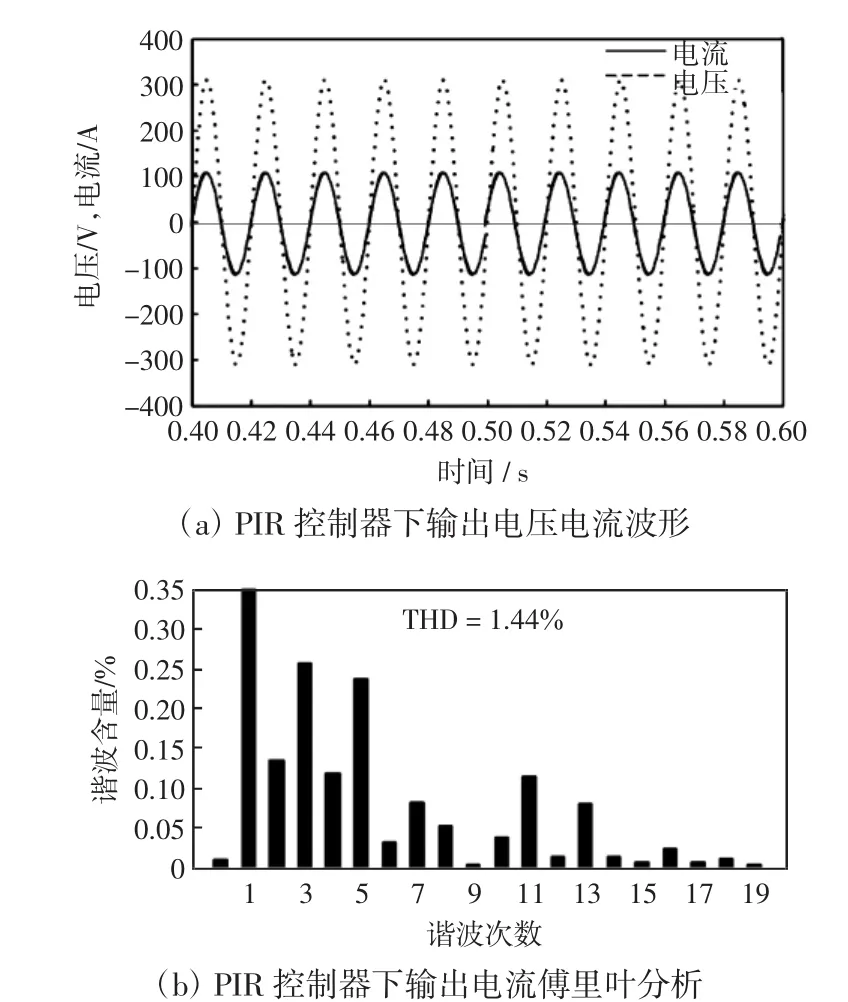
图9 采用PIR电流调节器逆变器输出电压电流波形及傅里叶分析Fig.9Simulation results of grid-connected inverter and Fourier analysis of output current based on PIR controller

5 结语

为了提高分布式发电系统的输出电能质量，抑制逆变器输出的低次谐波分量，本文将PIR电流调节器和简化三电平SVPWM算法应用于传统的电压、电流双闭环并网逆变器控制策略中。实验结果表明，上述方法能够有效地控制逆变器输出的谐波分量，输出电能质量明显改善，验证了所提出逆变器控制策略的正确性和有效性。

[1]鲁宗相，王彩霞，闵勇，等（Lu Zongxiang，Wang Caixia，Min Yong，et al）.微电网研究综述（Overview on microgrid research）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，31（19）：100-107．

[2]Ackermann T，Andersson G，Soder L.Distributed generation：a definition[J].Electric Power Systems Research，2001，57（3）：195-204．

[3]梁有伟，胡志坚，陈允平，等（Liang Youwei，Hu Zhijian，Chen Yunping，et al）.分布式发电及其在电力系统中的应用研究综述（A survey of distributed generation and its application in power system）[J].电网技术（Power System Technology），2003，27（12）：71-75，88.

[4]王成山，李琰，彭克（Wang Chengshan，Li Yan，Peng Ke）.分布式电源并网逆变器典型控制方法综述（Overview of typical control methods for grid-connected inverters of distributed generation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（2）：12-20.

[5]张纯，陈民铀，王振存（Zhang Chun，Chen Minyou，Wang Zhencun）.微网运行模式平滑切换的控制策略研究（Study on control scheme for smooth transition of microgrid operation modes）[J].电力系统保护与控制（Power System Protection and Control），2011，39（20）：1-5，10.

[6]张兴，陈玲，杨淑英，等（Zhang Xing，Chen Ling，Yang Shuying，et al）．离网型小型风力发电系统逆变器的控制（Inverter control of an isolated small scale wind power generation system）[J]．电力系统自动化（Automation of Electric Power Systems），2008，32（23）：95-99．

[7]马兆彪，惠晶，潘建（Ma Zhaobiao，Hui Jing，Pan Jian）.基于重复PI控制的光伏并网逆变器的研究（Study on photovoltaic grid-connected inverter based on repetitive-PI control）[J].电力电子技术（Power Electronics），2008，42（3）：25-27.

[8]李奇，陈维荣，刘述奎，等（Li Qi，Chen Weirong，Liu Shukui，et al）.基于虚拟磁链的质子交换膜燃料电池并网控制系统研究（Study on proton exchange membrane fuel cell grid-connected control system based on virtual flux-linkage）[J].电力系统保护与控制（Power SystemProtection and Control），2013，41（2）：91-96.

[9]黄如海，谢少军（Huang Ruhai，Xie Shaojun）.基于比例谐振调节器的逆变器双环控制策略研究（Double-loop digital control strategy based on proportional-resonant controller）[J].电工技术学报（Transactions of China Electrotechnical Society），2012，27（2）：77-81.

[10]马琳，金新民，唐芬，等（Ma Lin，Jin Xinmin，Tang Fen，et al）.小功率单相并网逆变器并网电流的比例谐振控制（Proportional-resonant gird-connected current control of low power single phase inverter）[J].北京交通大学学报（Journal of Beijing Jiaotong University），2010，34（2）：128-132.

[11]吴轩钦，谭国俊，张倩倩，等（Wu Xuanqin，Tan Guojun，Zhang Qianqian，et al）.新颖虚拟电网磁链在有源滤波器中的应用（Application of novel virtual line-flux-linkage observer in active power filter）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（6）：77-82.

[12]韩耀飞，谭国俊，侯周峰，等（Han Yaofei，Tan Guojun，Hou Zhoufeng，et al）.基于简化三电平SVPWM算法的逆变器研究（Study and realization of simplified SVPWM algorithm based on three level inverter）[J].电力电子技术（Power Electronics），2008，42（1）：6-8.

[13]王万宝，张犁，胡海兵，等（Wang Wanbao，Zhang Li，Hu Haibing，et al）.PR控制器对三电平半桥逆变器的均压研究（PR controller influence on voltage balance control for three-level inverter）[J].电力电子技术（Power Electronics），2013，47（6）：10-11，14.

[14]王凌，李培强，李欣然，等（Wang Ling，Li Peiqiang，Li Xinran，et al）.微电源建模及其在微电网仿真中的应用（Modeling of micro-powers and its application in microgrid simulation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（3）：32-38.

[15]韩肖清，曹增杰，杨俊虎，等（Han Xiaoqing，Cao Zengjie，Yang Junhu，et al）.风光蓄交流微电网的控制与仿真（Control and simulation of wind-PV-battery AC microgrid）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（3）：50-55.

[16]年珩，曾嵘（Nian Heng，Zeng Rong）.分布式发电系统离网运行模式下输出电能质量控制技术（Control technique on output power quality for distributed generation system under stand-alone operation mode）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（12）：22-28.

[17]Hu J，He Y，Xu L，et al．Improved control of DFIG systems during network unbalance using PI-R current regulators [J].IEEE Trans on Industrial Electronics，2009，56（2）：439-451．

[18]Liserre M，Teodorescu R，Blaabjerg F.Multiple harmonics control for three-phase grid converter systems with the use of PI-RES current controller in a rotating frame[J].IEEE Trans on Power Electronics，2006，21（3）：836-841.

关于论文中的图

1.图要精选，应具有自明性，切忌与表及文字表述重复。

2.图要精心设计和绘制，要大小适中，线条均匀，主辅线分明。

3.坐标图标目中的量和单位符号应齐全，并分别置于纵、横坐标轴的外侧。

4.图中的术语、符号、单位等应与表格及文字表述所用的一致。

摘编于《中国高等学校自然科学学报编排规范》（修订版）

Harmonic Suppression Methods for Grid-connected Inverter of Distributed Generation

HAN Ying，CHEN Wei-rong，LI Qi，LIU Zhi-xiang
（School of Electrical Engineering，Southwest Jiaotong University，Chengdu 610031，China）

In order to overcome the harmonics problems of voltage and current because of self-defect of proportionalintegral（PI）controller，a voltage-current close loop inverter control strategy based on proportion-integration-resonant（PIR）control method is proposed.Furthermore，a method of phase voltage reconstitution is proposed based on simplified 3-level SVPWM algorithm.The simulation result demonstrates that this control strategy can decrease the selected low order harmonics better.The inverter has superior output characteristic，and the correctness and feasibility of the control strategy is verified.

grid-connected inverter；proportional-integral-resonance（PIR）controller；3-level space vector pulse width modulation；phase voltage reconstitution；total harmonic distortion

TM46

A

1003-8930（2014）09-0001-06

韩莹（1990—），男，硕士研究生，研究方向为燃料电池并网技术、微电网运行与控制。Email：han_ying1009@163.com陈维荣（1965—），男，博士，教授，博士生导师，研究方向为燃料电池混合动力技术、智能信息处理等。Email：wrchen@home.swjtu.edu.cn

李奇（1984—），男，博士，副教授，研究方向为燃料电池并网技术、燃料电池混合动力技术等。Email：liqi0800@163.com

2014-01-23；

2014-03-27

国家自然科学基金项目（51177138）；高等学校博士学科点专项科研基金（20120184120011）；铁道部科技研究开发计划（2012J012-D）；四川省国际科技合作与交流研究计划（2012HH0007）；中央高校基本科研业务费专项资金项目（SWJTU11CX030）