大维随机矩阵的渐进特征
李 华,白志东,肖玉山
(1.长春大学理学院,吉林 长春130022;2.东北师范大学数学与统计学院,吉林 长春 130024)
大维随机矩阵的渐进特征
李 华1,白志东2,肖玉山1
(1.长春大学理学院,吉林 长春130022;2.东北师范大学数学与统计学院,吉林 长春 130024)
阐述了样本维数与样本量成比例趋于无穷时,大维随机矩阵特征向量子空间的极限特征.指出当随机矩阵列的谱具有谱分离的特征时,其特征向量子空间具有一定的渐进特征.
随机矩阵;谱分布;特征向量
1 预备知识

众所周知,当样本量n相对于样本维数p很大时,根据经典极限理论,样本方差将依概率收敛于总体方差矩阵.随着计算机技术的迅速发展,人们所面对的数据通常样本量和样本维数都很大,即样本维数往往相对于样本量是不可忽略的.这时继续使用样本方差作为总体方差的估计已经不再合适.人们迫切需要了解,在样本量相对于样本维数不充分大时,样本协方差矩阵与总体协方差矩阵之间的定量关系.
大维随机矩阵谱分析理论在描述样本协方差矩阵与总体协方差矩阵谱结构的定量关系方面做出了非常重要的贡献.[1]根据这一理论,我们知道当样本维数相对于样本量成比例趋于无穷时,在适当的条件下,Ap的经验谱分析(ESD)

(1)
将收敛于一个确定的分布.


为方程
(2)

特别的,当Σp=σ2Ip时,F为MP-law.这里Ip为p×p单位矩阵(见文献[3]).
有关Ap特征根的极限性质已经有大量文献进行研究.其中:文献[4]给出最大特征根的极限;文献[5]利用统一方法给出Σp=Ip时,Ap最大、最小特征根的极限;文献[6]证明了如果区间[a,b]位于F支撑集的外部,则对充分大的n,矩阵Ap无特征根落在区间[a,b]中.
目前有关Ap特征向量极限特征的文献还不是很多,相关结果可见文献[7-11].随着随机矩阵理论在诸如统计、无线通信、金融、经济等领域的应用,特征向量的极限特征逐渐引起人们的重视.例如在信号传输过程中,线性排列传感器所接收的信号,其到达方向(DOA)是基于信号的特征空间.在主成分分析和因子分析中,主成分方向是最大特征根对应的特征向量.
本文将讨论大维随机矩阵具有谱分离特征时,特征向量空间的极限特征.
2 谱分离
大维随机矩阵的谱分离结构最先由文献[6]和文献[12]提出.我们知道固定p,当n趋于无穷时,由大数定律可得Ap依概率收敛于Σp.自然地如果存在区间J⊂R+对所有充分大的n无Σp特征根落入J内,那么对于充分小的y(p→∞,p/n→y)应存在一个区间[a,b](J附近)对所有充分大的n,Ap无特征根落入[a,b]中,而且Ap的特征根落到[a,b]一侧的个数与Σp特征根落到J同一侧的个数是相同的.事实上,在适当的条件下,对于相对一般的y>0同样有类似的结论成立.
命题2.1[1]若:
(a) 设xij(i,j=1,2,…)是均值为0,方差为1且四阶矩有限的独立同分布随机变量;
(b)p=p(n),n→∞,yn=p/n→y>0;
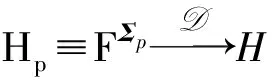
(d) ‖Σp‖(即Σp的谱模)有界;

(f) 对于充分大的n,区间[a,b](a>0)位于Fyn,Hp支撑集外的某个开区间内.
那么:
(1) 对于充分大的n,Ap依概率1无特征根落入[a,b]中;

(3) 如果y[1-H(0)]≤1,或y[1-H(0)]>1,但[a,b]不包含(0,x0),则对所有充分大的n,有区间
[-1/sFy,H(a),-1/sFy,H(b)]⊂R+
属于Hp支撑集的补.对这些n,如果ip≥0使得
亦即
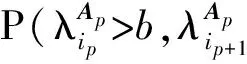
3 主要结论
这里我们考虑当Ap具有谱分离特征时,其特征向量的极限特征.
定理3.1 设在命题2.1条件(a)—(e)下.

(2) 对随机矩阵Ap进行谱分解
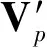
(3)
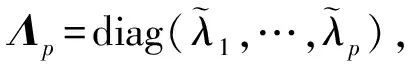
(3) 存在xl
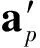
(ⅱ) 条件(4)中,我们要求向量列{ap},{bp}为单位向量,目的在于避免当p→∞时,‖ap‖(或‖bp‖)趋于无穷的情况,同时确保向量列的元素能在模一致的条件下进行分析.事实上此处的单位向量还可以变为任意其他确定的数值.


推论3.1可由定理3.2及条件(4)推得.
4 定理3.1的证明
设
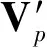





下面将证明
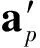
(4)

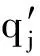
及
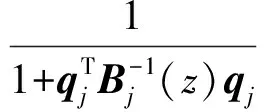
注意|βj(z)|≤|z|/v,‖Bj(z)-1‖≤1/v,由文献[6]中引理2.7,我们有
(5)
定义σ域流Fj=σ(q1,…,qj),记Ej(·)为给定Fj的条件期望,记E0(·)为非条件期望.
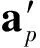


再由Borel-Cantelli引理,当r>2时,(4)式成立.
因为


(6)
(见文献[13]中等式(2.2)),我们有


(7)
这里:

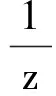
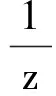
同(5)式,由文献[6]中引理2.7,对r≥2,
因此



由以上三个结论及(7)式可得
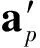
(8)

在定理3.1的条件下,

令z→0,

5 定理3.2的证明
在定理3.2的证明中,我们仅就i=1的情况进行了详细说明,i=2时可同理得到.



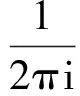
这里Γ1=u(C1).下面我们来分析一下围道Δ1,Δ2在围道内的极点情况.
首先考虑方程

(9)
设u1,u2为方程(9)的两个根,则有0 现在计算Δ. 对特定的Σp,我们针对不同的y=p/n分别计算Ap.这里我们给定总体协方差矩阵为对角矩阵,两个互异特征根分别为1和5,对应权重为0.5.给定样本量n=1 000,样本维数p=y×n,N=10 000为重复次数.针对不同的y=0.1,0.2,…,0.8,通过计算机模拟构造出Ap,求出特征根集合,并画出其直方图(见图1—2).从图1—2中我们不难看出,当y<0.4时,其矩阵Ap的特征根可以明显地分为两堆.正如命题2.1中结论(3)所描述的,这里一部分特征根集中在1附近,一部分集中在5附近.而当y=0.4,0.5时,虽然Ap特征根大致还能分为两堆,但特征根分离现象已经开始变得不十分明显.而当y>0.5时,Ap的特征根基本上已经变成一堆了. 图1 (y=0.1,0.2,0.3,0.4;λ=(1,5);w=(0.5,0.5);n=1 000;N=1 000)时Ap特征根直方图 图2 (y=0.5,0.6,0.7,0.8;λ=(1,5);w=(0.5,0.5);n=1 000;N=1 000)时Ap特征根直方图 表1为定理3.1的模拟验证结果,这里针对不同的y,计算 的均值和标准差,记为(·,·).从表1中可以看到,通过定理计算的 表1 定理3.1的模拟验证结果(λ=(1,5),w=(0.5,0.5),n=100,N=1 000) 表2为定理3.2的模拟验证结果,这里针对不同的y,分别计算了 的均值和标准差(i=1,2),分别记为AUiB,LAViB,EAViB(sdi)(i=1,2).这里我们就i=1的情况进行了详细说明.当y=0.1时,可以看到AU1B与EAV1B的差异并不大,只有0.007.但随着y的增加,这种差异逐渐变大,当y=0.8时,|AU1B-AV1B|=0.010 2.同时明显可以看到通过定理计算的LAV1B与AV1B均值的拟合效果很好,误差基本小于0.001,进而验证了定理3.2的结论.同样的,i=2的结果也进一步对定理3.2进行了验证. 表2 定理3.2的模拟验证结果(λ=(1,5),w=(0.5,0.5),n=100,N=1 000) [1] BAI Z D,SILVERSTEIN J W. Spectral analysis of large dimensional random matrices[M].2nd edition. Beijing:Science Press,2010:119-160. [2] SILVERSTEIN J W,BAI Z.D.On the empirical distribution of eigenvalues of a class of large dimensional random matrices[J]. Journal of Multivariate Analysis,1995,54(2):175-192. [4] YIN Y Y Q,BAI Z D,KRISHNAIAH. On the limit of the large eigenvalue of the largedimensional sample covariance matrix[J]. Probab Theory Related Fields,1988,78:509-521. [5] BAI Z D,YIN Y Q.Limit of the smallest eigenvalue of large-dimensional sample covariance matrix[J]. Ann Probab,1993,21:1275-1294. [6] BAI Z D,SILVERSTEIN J W. No eigenvalues outside the support of the limiting spectral distribution of large dimensional sample covariance matrices[J].Ann Probab,1998,26(1):316-345. [7] SILVERSTEIN J W. Weak convergence of random functions defined by the eigenvectors of sample covariance matrices[J]. Ann Probab,1990,18:1174-1193. [8] SILVERSTEIN J W. On the eigenvectors of large-dimensional sample covariance matrices[J]. J Multivariate Anal,1989,30:1-16. [9] SILVERSTEIN J W. Some limit theorems on the eigenvectors of large-dimensional sample covariance matrices[J]. J Multivariate Anal,1984,15:295-324. [10] BAI Z D,BAIQI MIAO,PAN G M.On asymptotics of eigenvectors of large sample covariance matrix[J]. Ann Probab,2007,35(4):1532-1572. [11] XIAN NINGNNG,QIN YINGLI,BAI ZHIDONG.Convergence rates of eigenvector empirical spectral distribution of large dimensional sample covariance matrix[J]. Ann Statist,2013,41(5):2572-2607. [12] BAI Z D,SILVERSTEIN J W. Exact separation of eigenvalues of large dimensional sample covariance matrices[J]. Ann Probab,1999,27(3):1536-1555. [13] SILVERSTEIN J W. Strong convergence of the limiting distribution of the eigenvalues strong convergence of the limiting distribution of the eigenvalues of large dimensional random matrices[J]. J Multivariate Anal,1995,55:331-339. [14] BAI ZHIDONG,LIU HUIXIA,WING KEUNG WONG.Enhancement of the applicability of markowitz’s portfolio optimization by utilizing random matrix theory[J].Mathematical Finance,2009,19(4):639-667. (责任编辑:陶 理) The asymptotic properties of the large dimension random matrix LI Hua1,BAI Zhi-dong2,XIAO Yu-shan1 (1.School of Sciences,Changchun University,Changchun 130022,China;2.School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China) This paper introduces the limiting behavior of the subspace of eigenvectors aspgoes to infinity with sample sizenproportionally.This paper establishes the asymptotic properties of the subspace of eigenvectors when the support to limiting spectral distribution is separate. random matrix theory;spectral distribution;eigenvectors 1000-1832(2014)04-0001-08 10.11672/dbsdzk2014-04-001 2014-08-01 国家自然科学基金资助项目(11171057,11171059);吉林省自然科学基金资助项目(201215113);吉林省教育厅课题(2010第160号);吉林省教育厅课题([吉教科合字]2014第272号). 李华(1977—),女,博士,讲师,主要从事概率统计研究;白志东(1943—),男,第三世界科学学院院士,博士,教授,博士研究生导师,主要从事应用概率与数理统计研究;通讯作者:肖玉山(1964—),男,博士,教授,主要从事概率统计研究. O 212.4 [学科代码] 110·6750 A
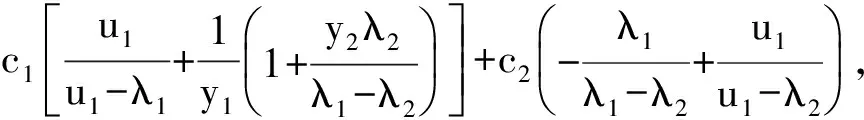

6 模拟验证









7 结论



