模型预测前向神经网络算法及其在组合导航中的应用

杨 一，高社生，吴佳鹏，赵 岩

（1.西北工业大学 自动化学院，西安 710072；2.航天恒星科技有限公司，北京 100086）

模型预测前向神经网络算法及其在组合导航中的应用

杨 一1，高社生1，吴佳鹏2，赵 岩1

（1.西北工业大学 自动化学院，西安 710072；2.航天恒星科技有限公司，北京 100086）

针对系统误差的不确定性可能会引起滤波精度降低或发散的问题，提出一种新的基于模型预测滤波的前向神经网络算法。首先，采用模型预测滤波估计网络在正向传递过程中的模型误差，并对其进行修正，以弥补模型误差对隐含层权值更新的影响；然后，利用模型预测滤波为神经网络提供精确的训练样本，学习待估计系统的非线性关系。将提出的算法应用于SINS/CNS/BDS组合导航系统，并与扩展卡尔曼滤波进行比较，仿真结果表明，提出的算法得到的姿态误差、速度误差和位置误差分别在[-0.25′,+0.25′]、[-0.05 m/s,+0.05 m/s]和[-5 m,+5 m]以内，滤波性能明显优于扩展卡尔曼滤波算法，表明该算法能提高组合导航定位的解算精度。

前向神经网络；模型预测滤波；权值修正；SINS/CNS/BDS组合导航

捷联惯导(SINS)/天文导航(CNS)/北斗卫星导航(BDS)组合导航系统兼备了SINS、CNS和BDS三者的优点，取长补短，不仅能够克服各导航子系统的缺陷，增强系统的完整性；而且可靠性好，定位精度高，是当前组合导航领域研究的热点之一。

在组合导航系统中，高精度滤波算法对导航定位的解算精度有重要影响。扩展卡尔曼滤波（Extended Kalman Filtering，EKF）是目前使用较广泛的非线性滤波算法之一，EKF算法通过Taylor展开来近似非线性系统模型，较好地解决了弱非线性系统的滤波问题，但由于忽略二阶以上误差项，在系统模型非线性较强时，EKF的滤波精度严重降低。要得到较精确的导航信息，需要高阶的卡尔曼滤波器，但这样会影响算法的实时性[1-2]。

近年来，神经网络技术已成功应用于系统状态的估计，神经网络算法无需对所求解的问题建模，通过学习所求解问题的样本关系可以很好地逼近其非线性特征[3-4]。由于神经网络的计算过程稳定，不涉及矩阵求逆，所以其计算耗时较少，有利于对导航数据处理的实时性。神经网络方法也存在一些缺点，对于组合导航这样复杂的时变系统，传统的前向神经网络算法无法直接得到输入与输出之间的映射关系[5]。针对这一问题，文献[6]提出基于卡尔曼滤波（Kalman Filtering,KF）的神经网络权值更新算法，并将提出的算法应用于惯导系统初始对准；仿真结果显示，在滤波精度相同的情况下，神经网络的实时性优于KF算法。但提出的算法只适用于线性系统，需要对神经网络模型进行线性化。文献[7]将输入状态稳定（ISS）理论与神经网络算法相结合，应用于含有未知死区的非线性系统识别，并证明该算法的有效性。但是该算法仅适用于离散系统且计算量大。文献[8]利用H∞滤波在线调整神经网络的权值，并将改进的神经网络算法用于SINS初始对准，仿真结果显示该算法具有较好的鲁棒性和实时性，但滤波精度有待提高。

模型预测滤波（Model Predictive Filtering，MPF）是一种基于非线性系统模型的实时滤波方法，其工作原理是利用预测输出跟踪测量输出，从而估计出系统的模型误差[9-10]。相比其他非线性滤波方法，预测滤波能够在线估计出任何形式的模型误差并对其进行有效修正。

本文在研究模型预测滤波和前向神经网络算法的基础上，提出一种新的基于模型预测滤波的前向神经网络权值修正算法。该算法利用模型预测滤波实时估计网络的模型误差，并对其进行修正，以弥补模型误差对权值更新的影响；利用学习后的神经网络算法控制系统噪声对导航解的影响，提高了导航系统的定位精度。将该算法应用于SINS/CNS/BDS组合导航系统进行仿真验证。结果表明，提出的算法滤波性能明显优于EKF算法。

1 模型预测滤波前向神经网络算法

1.1 模型预测滤波

模型预测滤波是一种适用于非线性系统模型的滤波算法，其原理是用滤波器的预测输出实时跟踪实际观测输出，从而估计出系统的模型误差。

设非线性系统方程为[10]：

式中，R是正定协方差阵。

系统状态估计和输出估计的关系如下：

观测估计的泰勒展开式为：

式中，

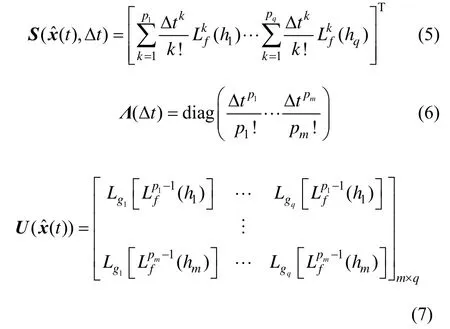
定义预测滤波性能指标函数如下[10]：

在[tk,tk+1]时间内满足式(8)性能指标的模型误差估计为：

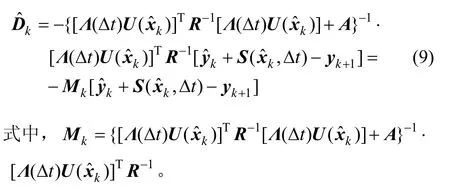
1.2 预测滤波-神经网络权值修正算法

前向神经网络由输入层、若干隐含层和输出层组成，各层由若干神经元组成。由Hecht-Nielsen定理[3]可知，任意一个三层前向神经网络，只要隐含层节点个数足够，就可以无限逼近任意非线性函数。三层前向神经网络结构如图1所示。

图1 前向神经网络结构图Fig.1 Structure of feed-forward neural networks

由图1可以看出，三层前向网络的传递关系为[3]：

式中，wji为输入层的第i个神经元到隐含层第j个神经元的连接权；jθ为隐含层第j个神经元的阈值；wkj为隐含层的第j个神经元到输出层的第k个神经元的连接权；kθ是输出层第k个神经元的阈值；p(·)为S型激活函数，满足：

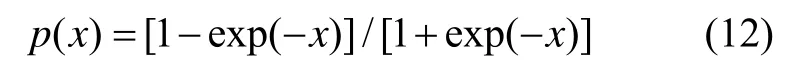
设第k个输出神经元的期望输出为yd，实际输出为yk，则系统均方误差为：

权值的更新是神经网络根据给定的学习样本进行训练的过程。在前向神经网络学习中，非线性特性的学习主要由隐含层完成，因此本文提出的权值更新算法针对隐含层，输出层权值仍由BP算法进行更新。

对于任意前向神经网络，假设隐含层每个神经元的输出为状态变量，输出层每个神经元的净输入为量测量。则前向网络的时变特性可用如下的状态方程和量测方程表示：

式中，w(t)是输出层的权值矩阵，为：

式中，n和m分别为输出层和隐含层的神经元个数。

在式(14)的状态方程中，ξ(t)为神经网络模型误差，由式(9)模型误差估计求得。神经网络中模型误差估计为：

由式(14)(19)可得到基于MPF的神经网络隐含层输出量的估计表达式，再由式(10)逆向推出隐含层权值矩阵。隐含层权值修正算法的步骤可归纳如下

① 初始化

置各层权值和阈值的初值为小的随机数；赋值误差函数e；设置循环次数R。

② 提供训练用的学习样本

输入矩阵x和经过模型预测滤波计算得到的目标输出yd；经过神经网络计算可得到真实输出yk。

⑦ 重复③～⑥进行隐含层权值更新，直至网络输出的均方误差满足给定的精度或者达到训练次数R，网络训练结束。

2 SINS/CNS/BDS组合导航系统模型

2.1 组合导航系统的状态方程

选东北天地理坐标系(E-N-U)为导航坐标系，在考虑系统模型误差和系统噪声的条件下，组合导航系统状态方程为：

式中，组合导航系统的状态向量选为

系统模型误差向量D(t)为：

式中，q为方程强度矩阵。

2.2 系统量测方程

1） SINS/CNS子系统量测方程

SINS误差方程解算出来的是实际建立的导航坐标系n与理想导航坐标系n′之间的平台误差角，建立平台误差角与姿态角误差的关系为：

则SINS/CNS组合导航系统量测方程为[1]：

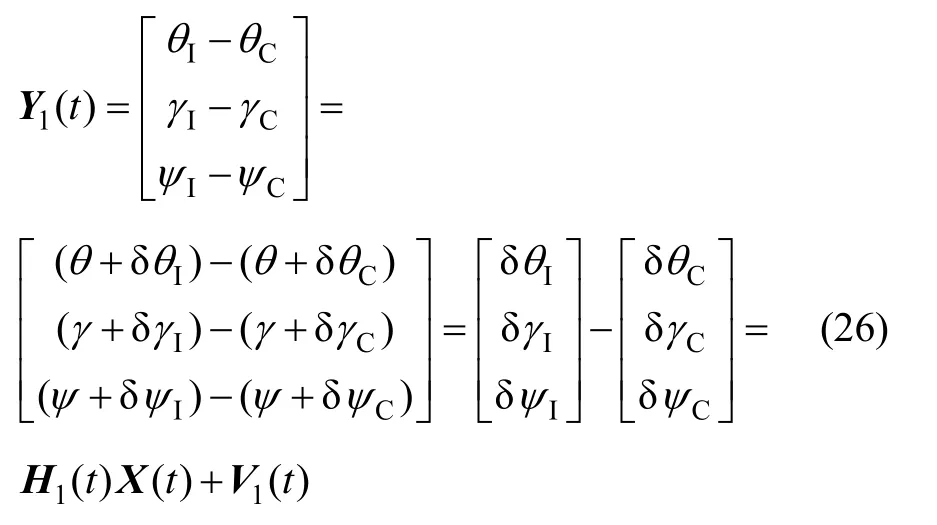
由式(25)(26)可得系统量测矩阵H1为：

2） SINS/BDS子系统量测方程

将SINS输出的速度、位置信息和BDS输出的速度、位置信息的差作为量测值，可得导航系统的量测方程为：

式中，LI、Iλ和hI分别为SINS的纬度、经度和高度信息，hB、LB和Bλ分别为BDS的高度、纬度和经度信息，δ·表示各项对应的误差，H2(t)为系统量测矩阵，V2(t)为系统量测噪声。

由式(21)(28)可得系统量测矩阵H2为：

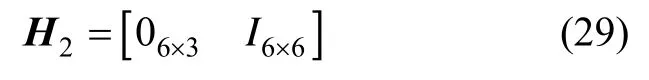
根据系统状态方程(20)和量测方程(26)(28)利用MPF算法估计系统状态，为神经网络模型提供精确的学习样本。

2.3 基于MPF的神经网络算法在组合导航中的应用

神经网络模型类似于“黑匣子”，只有输入和输出与外界发生联系。利用MPF为网络提供学习样本，并采用基于MPF的权值更新算法训练网络模型，当网络输出与样本值间的误差在允许范围内时，训练结束。网络的权值也随之确定，此时输入一组新的变量，可用此神经网络对系统进行精确估计。原理如图2所示。

由图2确定神经网络模型的非线性函数形式为：

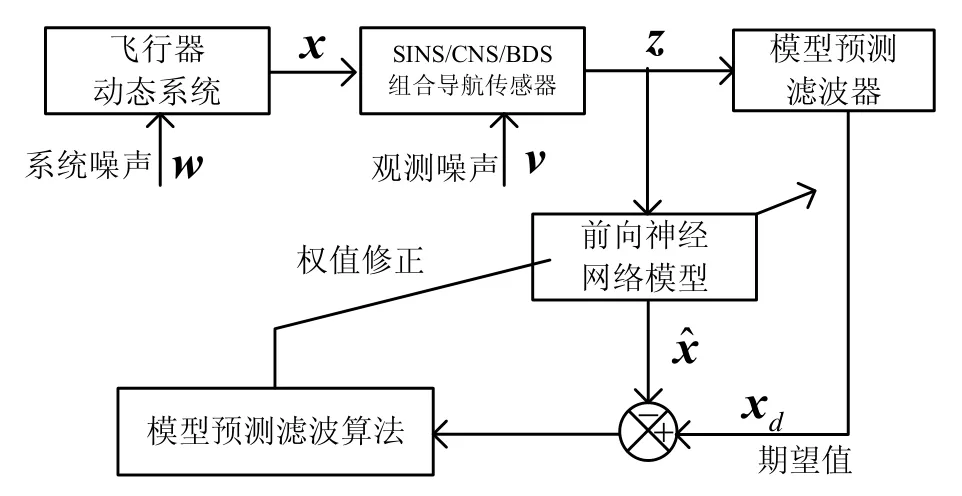
图2 基于预测滤波的神经网络算法应用于组合导航原理图Fig.2 Schematic diagram of neural networks based on MPF for integrated navigation system

隐含层神经元个数根据系统复杂程度，网络训练目标的精度以及训练速度等因素综合确定。如果节点太少，神经网络的收敛速度会变慢，甚至不易收敛；反之，节点选择过多，会引起神经网络的拓扑结构复杂，迭代计算量过大等问题。根据组合导航模型的复杂度，神经网络隐含层节点数可确定为：

式中，i为输入层节点数，k为输出层节点数，β是0～10之间的随机数。

3 仿真实验及分析

设飞行器的初始位置为东经109°，北纬34°，高度1200 m。陀螺的随机漂移为0.01(°)/h，随机游走为。加速度常值误差为 10-4g，随机游走为。SINS初始速度误差0.5 m/s，初始位置误差15 m；星敏感器的量测精度为20′，安装误差为20′；BD位置误差均方根为10 m，速度误差均方根为0.3 m/s；仿真时间为1000 s。误差统计结果如表1所示。仿真结果如图3～5所示。

表1 组合导航系统误差统计Tab.1 Integrated navigation systems error statistics

图3 位置误差估计Fig.3 Position error estimation

图3中虚线表示采用扩展卡尔曼滤波（EKF）计算得到的位置误差曲线，实线表示采用模型预测神经网络（MPNN）计算得到的位置误差曲线。通过对图3中误差曲线的分析和比较可以看出，EKF算法得到的东向、北向以及天向位置误差均在[-10 m,+10 m]之内；模型预测神经网络滤波算法计算得到的东向位置误差在[-5 m,+5 m]之内，北向位置误差和天向位置误差在[-4 m,+4 m]之内。

对图5中误差曲线的分析和比较可以看到，EKF算法计算得到的航向角、俯仰角和横滚角误差均为[-0 .5′,+0 .5′]；MPNN计算得到的航向角误差为[-0 .2′,+0 .2′]，俯仰角和航向角误差为。

图4 速度误差估计Fig.4 Velocity error estimation

图4中虚线表示采用扩展卡尔曼滤波（EKF）计算得到的速度误差曲线，实线表示采用模型预测神经网络（MPNN）计算得到的速度误差曲线。由图4可以看出，EKF算法计算得到的东向、北向和天向的速度误差均为[-0.1m/s,+0.1m/s]；MPNN计算得到的东向速度误差为[-0.05 m/s,+0.05 m/s]，北向速度误差和天向速度误差为[-0.06 m/s,+0.06 m/s]。

图5中虚线表示采用扩展卡尔曼滤波（EKF）得到的姿态误差曲线，实线表示采用模型预测神经网络（MPNN）计算得到的姿态误差曲线。

图5 姿态误差估计Fig.5 Attitude error estimation

4 结 论

针对系统误差的不确定性引起的非线性滤波精度降低或发散的问题，提出一种基于模型预测滤波的前向神经网络算法。将该算法应用于SINS/CNS/BDS组合导航系统进行仿真验证，并与扩展卡尔曼滤波进行比较。结果表明，提出的模型预测前向神经网络算法，滤波性能明显优于扩展卡尔曼滤波算法，不但算法的实时性好，而且能提高组合导航系统的解算精度。

（References）：

[1]赵岩，高社生，冯鹏程.临近空间伪卫星抗风场干扰自主导航[J].中国惯性技术学报，2013，21(3)：359-364.ZHAO Yan,GAO She-sheng,FENG Peng-cheng.Autonomous navigation of near space pseudolite under wind field disturbance[J].Journal of Chinese Inertial Technology,2013,21(3): 359-364.

[2]Wu Xiaojuan,Wang Xinlong.A SINS/CNS deep integrated navigation method based on mathematical horizon reference[J].Aircraft Engineering and Aerospace Technology,2011,83(1): 26-34.

[3]Yang Yi,Gao Shesheng,Zhao Yan.A novel stock decision model based on BP neural network[C]//2012 3rd International Conference on Intelligent Control and Information Processing: 317-321.

[4]Aboelmagd N,Ahmed E,Mohamed B.GPS/INS integration utilizing dynamic neural networks for vehicular navigation[J].Information Fusion,2011,12(1):48-57.

[5]Hamid M,Nitin K.T.Cascading artificial neural networks optimized by genetic algorithm and integrated with global navigation satellite system to offer accurate ubiquitous in urban environment[J].Computers,Environment and Urban Systems,2013,37(1): 35-44.

[6]王新龙，申功勋，唐德麟.基于最优估计神经网络的惯导系统初始对准研究[J].宇航学报，2002，23(3)：34-38.WANG Xin-long,SHEN Gong-xun,TANG De-lin.Initial alignment of the inertial navigation system based on a neural network suitable for the best estimation[J].Journal of Astronautics,2002,23(3): 34-38.

[7]Wen Yu.Nonlinear system identification using discretetime recurrent neural networks with stable learning algorithms[J].Information Sciences,2004,158: 131-147.

[8]刘国燕，徐晓苏，白宇骏.基于H∞滤波算法的前向神经网络在SINS初始对准中的应用[J].东南大学学报（自然科学版），2003，33(3)：331-334.LIU Guo-yan,XU Xiao-su,BAI Yu-jun.Application of feedforward neural networks based onH∞filter in SINS[J].Journal of Southeast University (Natural Science Edition),2003,33(3): 331-334.

[9]Sanaz M,Javad P,Mohammad R J,et al.Nonlinear model predictive control of a pH neutralization process based on Wiener-Laguerre model[J].Chemical Engineering Journal,2009,146(3): 328-337.

[10]高社生，宋飞彪，姜微微.抗差自适应模型预测滤波及其在组合导航中的应用[J].中国惯性技术学报，2011，19(6)：701-705.GAO She-sheng,SONG Fei-biao,JIANG Wei-wei.Robust adaptive model predictive filtering algorithm and application to integrated navigation[J].Journal of Chinese Inertial Technology,2011,19(6): 701-705.

Feed-forward neural network algorithm based on model predictive filtering and its application in integrated navigation

YANG Yi1,GAO She-sheng1,WU Jia-peng2,ZHAO Yan1
(1.School of Automation,Northwestern Polytechnical University,Xi’an 710072,China;2.Space Star Technology Co.,LTD.,Beijing 100086,China)

In view that the uncertainty of system errors may reduce the filtering precision or cause the problem of filter divergence,this paper proposes a novel feed-forward neural network algorithm based on model predictive filtering.First,a model predictive filtering(MPF) is used to estimate the neural network model errors in the forward transfer process and revise it to resist the impact on weights updating.Then,the MPF is used to provide accurate learning samples to neural network for approximating the nonlinear relationship.Finally,the proposed algorithm is applied to the SINS/CNS/BDS(SINS/celestial navigation system/BeiDou navigation satellite system) integrated navigation system and compared with extended Kalman filter (EKF).Simulation results demonstrate that the attitude angle error,velocity error and position error obtained by the improved neural network algorithm are within[-0.25′,+0.25′],[-0.05 m/s,+0.05 m/s]and [-5 m,+5 m],respectively,and the filtering performance is significantly superior to that of the EKF.The results show that the proposed algorithms effectively improve the positioning precision of the navigation system.

feed-forward neural network; model predictive filter; weights updating; SINS/CNS/BDS integrated navigation;

V249.32

：A

1005-6734(2014)02-0221-06

10.13695/j.cnki.12-1222/o3.2014.02.015

2013-11-20 ；

：2014-03-26

国家自然科学基金（61174193）；中国航天科技集团公司卫星应用研究院开放基金资助

杨一（1985—），男，博士研究生，研究方向为导航、制导与控制。E-mail：yangyi19850315@163.com

联 系 人：高社生（1956—），男，教授，博士生导师。E-mail：gshshnpu@163.com