IHS与多尺度变换结合遥感影像融合质量对分解层数的响应

方芳，张一平，赵琛琛，李劲澎，邓国臣

(1.66240部队，北京 100042；2.95806部队，北京 100076；3.信息工程大学 地理空间信息学院，郑州 450052；4.中国测绘科学研究院，北京 100039)

1 引 言

日益发展的遥感系统为用户提供了同一地区多空间分辨率、多光谱分辨率、多时间分辨率的海量遥感数据[1]。然而，受技术层面的制约，影像获取时影像的空间分辨率和光谱分辨率常常不可兼得，因此，亟需通过影像融合的方式获取高空间分辨率的多光谱影像。融合影像综合了原有影像各自的优势，减少了信息冗余，为后续影像信息的分析和应用提供了保证[2]。

目前常用的影像融合方法主要有3类：①直接对影像进行代数运算的方法，如加权融合方法、高通滤波方法、比值融合方法等；②基于空间变换的方法，如IHS、HSV、lαβ等色彩空间变换以及主成分变换等；③基于多尺度变换的方法，如基于影像的拉普拉斯金字塔分解与重建的方法，基于小波变换分解与重建的方法等[3]。其中，基于空间变换的融合方法能很好地提高影像的空间分辨率，但是会扭曲原有光谱信息；基于多尺度变换的融合方法将多分辨率分析应用于融合过程空间信息的提取，该方法对光谱信息的保持优于基于空间变换的融合方法，但会造成一定程度的影像的失真。对此，一些专家学者提出了基于IHS变换与多尺度变换结合的融合方法，徐建达等提出基于IHS变换和小波变换的遥感影像融合[4]，张一平等提出了基于IHS变换和NSCT的影像融合[5]。实验表明，IHS变换与多尺度变换相结合的融合方法能够取得比单一融合方法更好的融合效果。

多尺度变换的分解层数是影响融合效果的重要因素，分解层数越多，融合的频率范围越丰富，融合影像所包含的空间细节信息越来越丰富，然而并不是分解层数越多影像融合的质量就越高。邢素霞对基于小波变换影像融合的分解层数进行了分析探讨[6]，但未讨论与IHS结合的效果及论文最佳分解层数的适应性。本文围绕该问题，分别对IHS变换与3种多尺度变换相结合的融合方法及融合效果与分解层数的关系进行了探讨。

2 融合原理与方法

2.1 基于IHS变换的融合方法

IHS色彩空间采用相关性很低的强度(I)、色度(H)和饱和度(S)3个分量表示颜色，将影像的强度分量和光谱信息分离，更加有利于影像的融合。该方法的思想是先将高光谱影像由RGB空间变换到IHS空间，然后用处理过的高空间分辨率影像替换高光谱影像的I分量，最后将融合后的影像变换回RGB空间。

2.2 基于多尺度分解的融合方法

该方法的思想是将高空间分辨率的全色影像和多光谱影像分别进行多尺度分解，实现影像高低频信息的分离，再分别进行融合处理，把多光谱影像所不具有的空间细节信息尽可能的注入到融合影像中，从而在保证融合影像光谱信息的条件下尽可能提升空间分辨率。本文对拉普拉斯金字塔变换、提升小波变换、非下采样Contourlet变换等多尺度分解方法进行了讨论。

(1)拉普拉斯金字塔变换

拉普拉斯金字塔变换是一种常用的影像多尺度分析方法，它由高斯金字塔中相邻两层影像相减得到的近似影像构成，可以突出表示不同尺度的影像细节。拉普拉斯金字塔的每层分别保留了不同尺度的高频信息，能很好的突出影像细节，对于影像进一步分析和处理具有重要意义。

(2)提升小波变换

提升小波变换继承了传统小波时频局部化等特性，具有计算速度快、节省内存空间、容易实现反变换等优点，可以通过整数小波变换，精确的重构原始信号，非常有利于影像的各种处理。与拉普拉斯金字塔每层分解只能得到1个近似低频分量和1个高频分量相比，提升小波变换能够得到1个近似低频分量和3个方向的高频分量。因此，提升小波变换分离影像高低频信息的效能较拉普拉斯金字塔变换好，理论上利用其进行影像融合的效果也更好。

(3)NSCT(非下采样Contourlet变换)

NSCT由非下采样金字塔结构和非下采样方向滤波器组构成，非下采样金字塔将输入的图像分解为低频子带和高频子带，实现图像的多分辨率分解；利用非下采样方向滤波器组，将高频子带分解为2n个方向子带；每一层的低频子带重复上述操作。NSCT是Contourlet变换的一种改进，有效解决了Contourlet变换因下采样而产生的平移性和频谱混淆问题，克服了小波变换在面临线或面奇异处理时的不足。

2.3 IHS变换与多尺度变换结合的融合方法

IHS变换与多尺度变换结合的融合过程如下：

①通过IHS变换将多光谱影像从RGB空间转换到IHS空间；

②将多光谱影像的亮度分量I与全色影像分别进行相同级数的多尺度变换，分解得到各影像不同层次、不同方向的高频和低频分量；

③采用不同的融合策略分别对分解得到的不同尺度的高低频子带影像进行融合处理；

④对融合后的高低频子带影像进行影像重建，得到新的亮度分量Inew；

⑤用新的亮度分量Inew替换原始影像的亮度分量I，将其与原始多光谱影像的H、S分量一起变换到RGB空间，得到融合影像。

低频子带融合规则：设两幅影像经多尺度变换后的低频部分别为IA和IB，在融合时，采用式(1)给定的权值融合法，权值大小由低频子带的区域能量自适应来确定：

IL(x，y)=wAIA(x，y)+wBIB(x，y)

(1)

其中，wA和wB分别表示权值大小，由式(2)计算得到

(2)

式中，E(x，y)=∑m，n∈SM×N(I(x+m，y+n))2代表区域能量，SM×N表示区域窗口大小，本文采用的区域窗口大小为3×3。

高频子带融合规则：高频子带主要反映图像的细节信息，为了突出影像局部的对比度，充分考虑中心像素与周围像素的相关性，采用高频系数与其邻域系数的8个方向的梯度变化作为像素选取的阈值。设融合后影像的各层、各方向高频系数为Ij，k(以NSCT为例，其中Ij，k表示的是NSCT分解后第j层，k方向的高频子带)，则有：

(3)

式中T(x，y)定义为：

(4)

融合过程步骤②中多尺度变换给出的分解层数决定了融合处理所处的分解层，直接影响融合的效果，下面对不同分解层数的融合效果进行分析。

3 融合实验与分析

本文对多组遥感影像进行了相应实验，为了便于直观展示，选取其中一组QuickBird全色影像和多光谱影像进行说明，图像大小为像素512×512像素，如图1所示。

图1 QuickBird全色影像和多光谱影像

3.1 融合质量综合评价指标

公式(5)为平均梯度的计算式，ΔxZ(i,j)、ΔyZ(i,j)分别是图像在行、列方向的灰度差。

(5)

平均梯度可以反映影像对微小细节反差的表达能力，可用来评价影像的清晰度，平均梯度越大，影像灰度变换率越大，影像越清晰，即影像对微小细节的表达能力越强。

公式(6)给出了标准差的定义，其中的μ为影像所有像元亮度值的算术平均值。

(6)

标准差描述了像元值与影像均值的离散程度，可以用来评价影像的反差大小，标准差越大，说明影像灰度级分布越分散，影像的反差越大；标准差越小，影像的反差越小。

(7)

UIQI是一种综合评价指标，它从相关信息损失、辐射值扭曲以及对比度扭曲几个方面来评价融合影像与原多光谱影像的相似程度。UIQI取值范围为[0，1]，其值越大，表示融合影像与原多光谱影像光谱信息越接近，融合效果越好。

分析可得，平均梯度、标准差和UIQI 3项指标越大，融合影像的空间分辨率越高，光谱扭曲越小，融合效果越好。

3.2 融合结果及质量分析

利用本文提到的3种融合方法分别对影像进行1～6层多尺度分解后的融合实验，图2为3项客观评价指标随层数增长的走势。

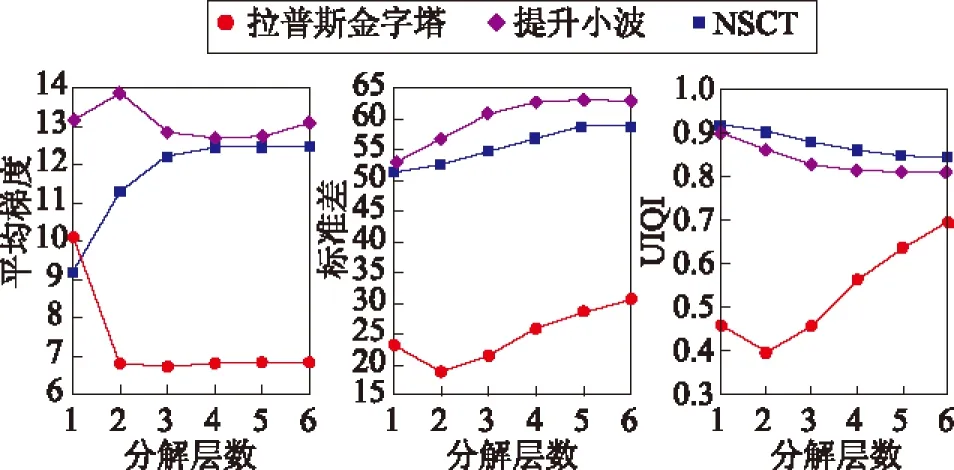
图2 融合的评价指标对多尺度分解层数的响应曲线图

通过指标分析(图2)和对实验结果(图3～图5)的观察，可得到以下结果：

图3 IHS变换与拉普拉斯金字塔变换的融合效果。

图4 IHS变换与提升小波变换的融合效果。

图5 IHS变换与NSCT变换的融合效果。

①对基于拉普拉斯金字塔变换融合方法分解的3项融合质量客观评价参数，第1层与其他4层走势大不相同，通过目视观察融合影像可以发现，这是因为用拉普拉斯金字塔变换融合方法对影像进行1层分解的融合影像出现了明显的分块现象，使得融合影像严重失真(如图3(a)所示)，导致客观评价参数可靠性降低，出现了跳跃性变化。而当分解层数逐步增加时，其平均梯度波动较小，而标准差和综合指标UIQI均呈现稳步上升的趋势，这说明随着分解层数的上升，其融合质量越来越好，到第5层时，趋于平稳，在第6层分解时，达到较好的融合效果。但总体来说，其融合效果不如基于提升小波变换和NSCT的方法。

②对于基于提升小波变换的融合方法，平均梯度第2层时达到峰值，在前3到5层分解时变化比较稳定，而标准差随着分解层数的增加呈现出稳步增长的趋势，这说明分解层数越多，融合影像的标准差越大，影像的反差越大。而UIQI指数则是随着分解层数的增加呈逐渐递减的趋势，说明融合影像随着分解层数的增加，光谱失真越大。综合空间分辨率和光谱信息两方面考虑，对基于提升小波变换的方法，分解层数为2时，能相对取得较好的融合效果。

③对于基于NSCT的融合方法，在1到3层分解时，其平均梯度随着层数的增加而不断增加，到第3层达到最大值。其后随着分解层数的增加，平均梯度趋于稳定，而没有像基于小波变换的融合方法那样出现较大波动，这是由于NSCT具有平移不变特性，其不会随着分解层数的增加而产生严重的频谱混叠现象。其标准差和UIQI指数的走势与基于小波的融合方法大致相同，但是其标准差整体上不如小波变换，而UIQI指数则在整体上优于小波变换，这说明虽然基于NSCT的融合方法得到的融合影像的标准差不如小波变换，但它比小波变换具有更好的光谱保持能力，因此，选取3层分解比较适合影像的融合处理。

4 结束语

本文针对单一融合方法存在的不足，研究了IHS变换与拉普拉斯金字塔变换、提升小波变换和NSCT 3种多尺度变换方法相结合的融合方法，概要分析了3种融合方法的优缺点，详细研究了多尺度分解层数对融合效果的影响，得到了对于影像融合相对合适的多尺度分解层数。实验证明，IHS变换与提升小波变换相结合的方法以及IHS变换与NSCT相结合的方法明显优于IHS变换与拉普拉斯金字塔变换相结合的融合方法；基于拉普拉斯金字塔变换的融合方法在6层分解时为最佳融合效果；基于提升小波变换的融合方法在分解层数为两层时，能取得较好的融合效果；对于NSCT变换，在3层分解比较适合影像的融合处理；而IHS变换与NSCT相结合的方法能在提高融合影像空间分辨率的同时，更好地保留原多光谱影像的光谱信息，与其他两种方法相比，该方法获得的融合影像色彩自然，边缘清晰，综合融合效果更好。

参考文献：

[1] 姜芸，臧淑英，王军.多源遥感影像数据融合技术研究[J].测绘与空间地理信息，2005，32(2)：46-50.

[2] 张丽侠，张力，艾海滨.改进HIS变换的图像融合方法研究[J].测绘科学，2011，36(6)：149-151.

[3] 徐青，张艳，耿则勋.遥感影像融合与分辨率增强技术[M].北京：科学出版社，2007：75.

[4] 徐建达，王洪华.基于HIS变换和小波变换的遥感影像融合[J].测绘学院学报，2002，19(3)：198-199.

[5] 张一平，龚志辉，胡玲，等.基于非下采样Contourlet变换的遥感影像融合[J].测绘科学技术学报，2012，29(3)204-208.

[6] 邢素霞.多光谱图像融合中小波分解层数研究[J].微电子学与计算机，2011，28(1)：176-179.