面向遥感卫星数据获取应用的时间序列云量预测方法
王志信,黄鹏,林友明,贾秀鹏
(1.中国科学院大学,北京 100049;2.中国科学院遥感与数字地球研究所,北京 100094)
1 引 言
为满足全球矿产资源、作物估产、水资源、森林生态和城市变化检测等应用领域的特定数据获取需求,遥感技术特别是光学遥感技术在其中发挥了重要作用[1-4]。在光学遥感数据获取应用中,对于特定目标区域,如果在云量覆盖较多的时候进行卫星成像规划,则容易得到利用价值较低的多云数据,同时也会造成卫星资源的浪费,而如果能提前预知云量覆盖情况,选择云量覆盖较少的时段进行卫星成像规划,则更有利于获取到满足遥感应用需求的少云或无云数据。因此,如何进行云量预测,以获取优质的能满足遥感应用需求的无云或少云数据,便成为了一个重要问题。
然而,目前还没有直接面向卫星成像规划的云量预测方法。在云量预测相关模型方法方面,应用较多的是与气象相关的短期预测模型,此类模型主要是利用一些模型方法,如模式识别、交叉相关法等来对云变化进行短期预测[5-6],预测期通常为几小时。例如,利用卫星云图对一个热带飓风进行为期几小时的短期预测。而一般卫星成像规划所需要的预测时间长度要远大于几小时,此类短期预测模型对于卫星成像规划来说实际应用价值不大。还有一类有代表性的模型即人工神经网络模型(Artificial Neural Network,ANN),这是一种应用于对大脑神经突触联接的结构进行信息处理的数学模型。它具有很多优点,如自学习功能,这对于预测有特别重要的意义,还具有联想存储功能、具有高速寻找优化解的能力等[7-8]。虽然神经网络模型的这些优点使它可以应用于云量预测,但是由于影响云分布的因素众多,且卫星规划的区域范围不定,大到国家小到城市都有可能,这中间牵涉到的众多因素将导致神经网络中节点的确定和学习过程非常复杂,因而,很难建立一个能够全面描述并准确预测大范围云量的模型。这使得神经网络模型也不太适用于卫星数据获取所要求的云量预测。
为了解决传统云量预测模型不能满足遥感实际应用需求的问题,本文采用时间序列分析预测的方法,对云量进行预测。首先,针对云量数据本身具有时间序列的特点,对云量进行分类。然后,在分类的基础上对不同的类型采取不同的模型进行预测,最终得到云量预测结果,从而避免考虑众多的云量影响因素导致建模困难的问题,利用云量预测结果信息可为卫星成像规划提供参考,有利于更好地获取无云或少云数据,减少卫星资源的浪费,满足遥感数据应用需求具有重要的现实意义。
2 时间序列分析建模方法
1927年,英国统计学家G.U.Yule(1871~1951)提出了自回归(Auto Regressive,AR)模型。不久之后,英国数学家、天文学家G.T.Walker爵士在分析印度大气规律时使用了滑动平均(Moving Average,MA)模型和自回归滑动平均(Auto Regressive Moving Average,ARMA)模型(1931年)。这些模型奠定了时间序列时域分析方法的基础。1970年,美国统计学家G.E.P.Box和英国统计学家G.M.Jenkins联合出版了《时间序列分析—预测与控制》一书(文献[9])。在书中,Box和Jenkins在总结前人研究的基础上,系统地阐述了对求和自回归滑动平均(Autoreg Ressive Integrated Moving Average,ARIMA)模型的识别、估计、检验及预测的原理及方法。这些时间序列分析的方法,已经成为时域分析方法的核心内容。
2.1 ARMA模型
自回归滑动平均模型(Auto Regression Moving Average,ARMA)是目前最常用的拟合平稳序列的模型。其模型结构如下:
(1)
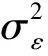
ARMA(p,q)模型可以简写为:
xt=φ1xt-1+φ2xt-2+…+φpxt-p+εt-θ1εt-1-θ2εt-2-…-θqεt-q
(2)
引进延迟算子,ARMA(p,q)模型简记为Φ(B)xt=Θ(B)εt。其中,Φ(B)=1-φ1B-φ2B2-…-φpBp,为p阶自回归系数多项式。Θ(B)=1-θ1B-θ2B2-…-θqBq,为q阶滑动平均系数多项式。当q=0时,ARMA(p,q)模型就退化成了AR(p)模型;当p=0时,ARMA(p,q)模型就退化成了MA(q)模型。所以,AR(p)模型和MA(q)模型实际上是ARMA(p,q)模型的特例,它们都统称为ARMA模型。
2.2 ARIMA模型
ARMA(p,q)模型描述的是平稳时间序列,然而在实际工作中遇到的很多都是非平稳时间序列。为了将其平稳化,通常利用一次差分或多次差分运算把原时间序列转化成平稳时间序列。一个时间序列如果能通过差分运算转化为平稳时间序列,则称这个非平稳时间序列为差分平稳时间序列。对差分平稳时间序列可以使用ARIMA模型进行拟合。
2.2.1 差分运算

2.2.2 ARIMA模型
具有如下结构的模型称为求和自回归移动平均(Autoreg Ressive Integrated Moving Average)模型,简记为ARIMA(p,d,q)模型:

(3)

(4)
2.3 SARIMA模型
在某些时间序列中,存在着明显的周期性变化。这种周期性是由于季节性变化(包括季度、月度、周度等变化)或其他一些固有因素引起的,这类序列称为季节性序列。描述这类序列,本文用季节时间序列模型(Seasonal ARIMA model,SARIMA)表示。当序列具有短期相关性时,通常可以使用低阶ARMA(p,q)模型提取。当序列具有季节效应,季节效应本身还具有相关性时,季节相关性可以使用以周期步长为单位的ARMA(P,Q)模型提取。由于短期相关性和季节效应之间具有乘积关系,所以拟合模型实质为ARMA(p,q)和ARMA(P,Q)的乘积。综合前面d阶趋势差分和D阶以周期S为步长的季节差分运算,对原观察值序列拟合的乘积模型完整的结构如下:
(5)
式中:Θ(B)=1-θ1B-…-θqBq,ΘS(B)=1-θ1BS-…-θQBQS,Φ(B)=1-φ1B-…-φpBp,ΦS(B)=1-φ1B-…-φPBPS。该乘积模型简记为ARIMA(p,d,q)×(P,D,Q)S。
3 实验方法设计
3.1 数据源
数据源采用ISCCP的D2云数据集。国际卫星云气候研究计划(ISCCP)成立于1982年,作为世界气候研究计划(WCRP)之一,它主要通过收集和分析气象卫星辐射测量值来研究全球云分布、属性以及每日、每季和每年的变化。其生产的数据集不仅可以用来研究云在气候变化中所扮演的角色,还可以用来研究云在辐射能量交换中所起的作用以及它在全球水循环中所起的作用[10-11]。ISCCP提供的云量数据分为不同的类别,主要包括:B3和BT级别,大气数据,海冰和雪数据,DX、D1、D2级别。其中,D2数据是所有级别数据当中具有最优质云量信息的数据,在云量研究中应用广泛,因而数据源选择D2数据集。
3.2 实验方法
3.2.1 数据读取及分类
读取ISCCP的D2数据集中与云量有关的数据并提取云量网格的历史云量特征,对全球云量网格进行分类按照ISCCP数据集的说明读取云气候学数据中的月平均云量数据后,针对云量数据的时空分布各异的特征首先对全球云量网格进行分类,在此基础上针对不同特征进行相应的建模预测。
首先,判断每个网格的月平均云量时间序列的平稳性。判断某个序列Xi的平稳性主要是通过单位根检验,判断标准为ADF检验(Augmented Dickey-Fuller)。构造ADF检验统计量:是参数ρ的样本标准差。当τ 大于DW临界值,则序列存在单位根,是非平稳序列。反之则为平稳序列。在此基础上,对于非平稳序列,进一步判断序列是否具有季节性;主要判断标准为自相关函数ACF(AutoCorrelation function)。自相关函数ρt,sρt,s=Corr(xt,xs),t,s=0,±1,±2,…,其中,{xt,t=0,±1,±2,…}是随机过程。具有季节性的云量时间序列的ACF具有季节周期为12的周期性特征,即若某序列的ACF在滞后期12的整数倍出现峰值,则该序列存在季节性特征,反之,则序列不存在季节性特征。
其次,根据分类结果选择合适的模型。采用分类树分类方法对全球云量网格进行分类:对时间序列是否平稳进行判断;进一步对时间序列是否存在季节性进行判断,将全球云量网格分为以下3类:
分类①:月平均云量时间序列平稳类型;
分类②:月平均云量时间序列不平稳,同时具备季节周期性变化,即月平均云量时间序列季节非平稳类型;
分类③:月平均云量时间序列不平稳,不具备季节周期性变化,即月平均云量时间序列普通非平稳类型。
3.2.2 选取模型
针对不同的云量类型,选取相应的模型进行预测:
对于分类①,选择建立平稳时间序列模型——ARMA模型;
对于分类②,选择建立非平稳季节性时间序列模型——SARIMA模型;
对于分类③,选择建立非平稳时间序列模型——ARIMA模型。
3.2.3 数据预处理
选取模型之后,根据不同的模型要求,对历史云量数据进行相应的处理。ARMA模型可以直接应用原始数据;ARIMA模型则需要在结合检验平稳性的基础上,对数据进行差分处理;季节性SARIMA模型需要结合检验平稳性的基础上,根据需要对数据进行季节差分和普通差分处理。
3.2.4 参数估计
根据历史云量数据和相应的模型,需要对模型进行参数估计。一般情形下,参数估计分两步工作,第1步,找出参数的初步估计或称参数的初始估计,利用样本自相关函数对模型参数进行初步估计,例如对ARMA模型的特例AR(P)模型具体可利用Yule-Walker方程进行参数估计。第2步,在初步估计的基础上,按照一定的估计准则,求得模型参数的精细估计。模型参数的估计计算复杂,需要由计算机完成。
3.2.5 模型诊断
为确定模型拟合是否充分,对残差进行分析,检验残差的同方差性、正态性和独立性,检验残差是否接近白噪声,同时考虑过度拟合和参数冗余,对模型做出相应修正。
3.2.6 预测
基于最小化的均方预测误差方法,利用第i个网格云量数据和相应模型对云量进行预测,得出该网格未来数月的云量预测结果数据。对于某序列Xi来说可获得直到时间t的历史数据,即x1,x2,…xT-1,xT,预测未来e期的值xe+t,称时间t为预测起点,e为预测前置时间,用xt(e)代表预测值,最小均方误差预测如下:xt(e)=E(xe+t|x1,x2,…xT-1,xT)。它的原理是用x1,x2,…xT-1,xT(为方便起见记为y)的函数来预测x,标准是最小化均方误差,这里需要选择函数h(y),使得下式达到最小:E[x-h(y)]2根据概率论条件期望性质,上述式子可写为:E{[x-(y)]2|Y=y}=E{[x-h(y)]2Y=y},因此对于每个y,h(y)的最优选择都是h(y)=E(x|Y=y),因而h(y)的这一选择可使得E[x-h(y)]2整体达到最小,因此,h(y)=E(x|Y)是基于所有y的函数所得的x的最优预测[12]。
4 实验及结果
4.1 2007年平均云量预测实验
选取北京地区为感兴趣区,在时间上选取1984年至2006年间22年的月平均云量数据。利用此历史云量数据对2007年12个月的月平均云量进行预测,得到12个月份的月平均云量预测值并与2007年份真实云量值进行对比验证。
提取北京地区所在网格的月平均云量时间序列;判断月平均云量时间序列的平稳性。

图1 1984年到2006年北京地区云量序列图

图2 北京地区云量序列自相关函数图
北京地区云量序列的ACF如图2所示。从图中可知该序列是非平稳的,并且具有明显的季节性特征。采用ADF检验,h=0检验的P值:pValue=0.3543,样本统计量:stat=-0.8112,拒绝临界值:cValue=-1.9417,由此可见属于第2类,模型识别为SARIMA模型。季节性SARIMA模型需要在检验平稳性的基础上,根据云量数据本身特点对数据进行一次季节差分和一次普通差分处理,采用SARIMA模型进行分析预测后得出预测值,并跟真实值进行验证。
如图3所示,用1984年到2006年22年数据预测2007年12个月云量。得出2007年12个月份的预测值,预测值的80%、95%置信区间。与2007年实际值比较,实际真实值均落在80%置信区间内,平均相对误差3.60%,最大相对误差5.29%,均方误差3.2199。
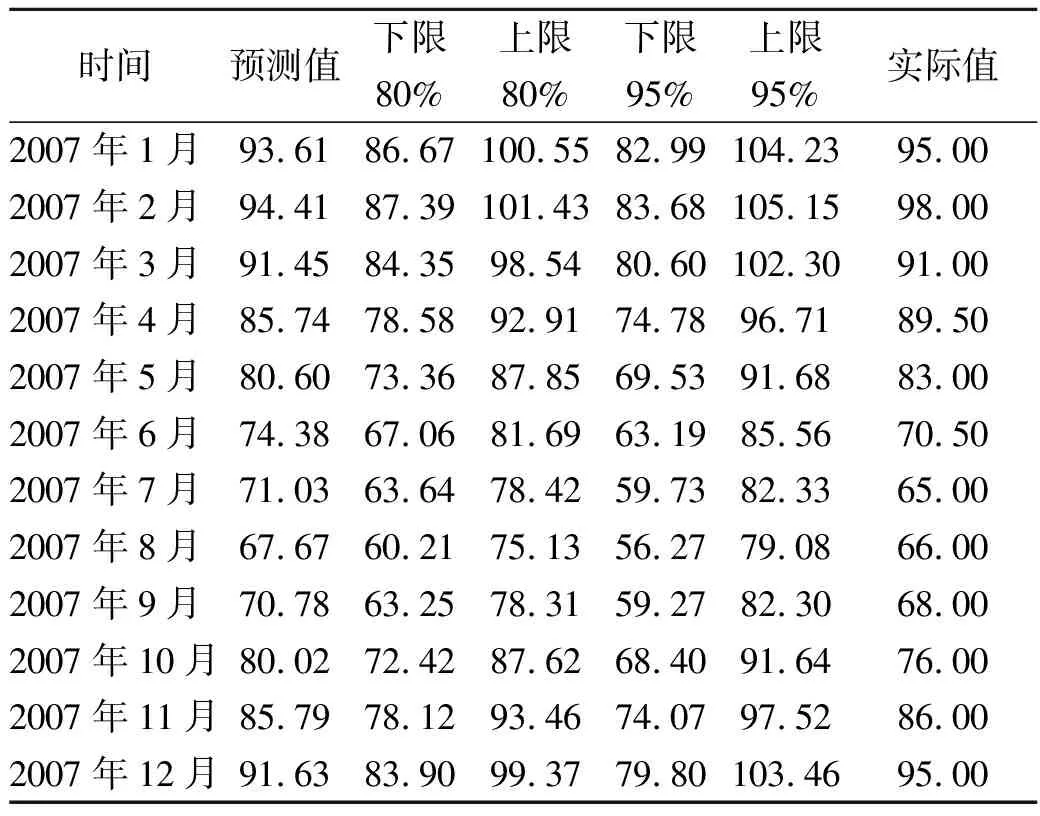
表1 北京地区2007年预测值与实际值
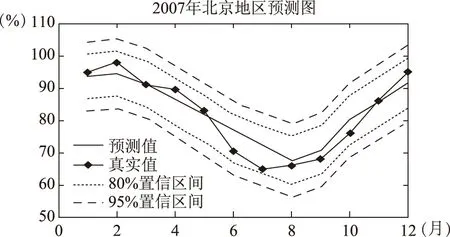
图3 利用1984年到2006年22年数据预测2007年12个月份的预测图
4.2 1997年平均云量预测
仍选取北京为感兴趣区,但在时间上选取1984年到1996年的12年月平均云量数据,对1997年进行预测值并与1997年实际值进行比较,结果显示,9月份实际值落在95%置信区间,其余月份实际值均落在80%置信区间内,平均相对误差4.18%,最大相对误差15.29%,均方误差4.2902。

表2 北京地区1997年预测值和实际值

图4 利用1984年到1996年12年数据预测1997年12个月份的预测图
4.3 2009年平均云量预测实验
选取乌鲁木齐为感兴趣区,在时间上选取1984年到2008年间24年月平均云量数据对2009年份12个月份月平均云量进行预测和验证,结果显示,2009年12个月份的预测值,预测值的80%、95%置信区间。与2009年实际值比较,实际值除一月份落在95%置信区间外,其余月份均落在80%置信区间内,平均相对误差2.80%,最大相对误差6.55%,均方误差2.8871。

表3 乌鲁木齐地区2009年预测值与实际值

图5 利用1984年到2008年24年数据预测2009年12个月份的预测图
4.4 预测结果分析
由以上实验结果可知,绝大部分云量实际值落在云量预测80%置信区间之内,而且,不论是利用10年还是20年的历史数据,均能得到精度较好的结果,说明此方法的时间适应性较好。更为重要的是,云量预测结果较准确地反映了云量的变化趋势,这对于卫星成像规划具有很重要的意义,利用云量变化趋势信息,可在长周期卫星成像规划中发挥重要参考作用。以北京为例,根据云量预测参考信息,要想获取此地区的少云数据,应该尽量选取云量低的7、8和9月份来进行规划,相比在12、1和2月则更容易获取到满足遥感应用需求的数据。
5 结束语
针对目前没有能够直接满足遥感数据获取需求相关的云量预测方法的问题,本文提出了一种利用时间序列分析预测方法对云量进行预测的方法。在云量特征分类的基础上,整合ARMA、ARIMA和SARIMA 3种模型对云量进行预测,并得到了满意的预测结果。根据云量预测结果参考信息,选择云量覆盖较少的时间段进行卫星成像规划,有利于更合理的进行卫星成像规划,对满足遥感数据获取需求有重要意义。由于云量本身的复杂性以及当前云量预测研究还处在初步研究阶段,本方法仍存在一定的不足,如为了更好地满足卫星成像规划的实际需求,以月为单位的预测结果在时间分辨率上还有待提高,更精确的预测方法还有待进一步研究。
参考文献:
[1] SANKEY J B,WALLACEB C S,RAVIC S.Phenology-based remote sensing of post-burn disturbance windows in rangelands[J].Ecological Indicators,2013(30):35-44.
[2] TULBURE M G,BROICH M.Spatiotemporal dynamic of surface water bodies using Landsat time-series data from 1999 to 2011[J].Journal of Photogrammetry and Remote Sensing,2013,79(2013):44-52.
[3] JAWAK S D,LUIS A J.Improved land cover mapping using high resolution multiangle 8-band WorldView-2 satellite remote sensing data[J].Journal of Applied Remote Sensing,2013,7(1):73-86.
[4] HANSSAN Q K,RAHMAN K M.Remote sensing-based determination of understory grass greening stage over boreal forest[J].Journal of Applied Remote Sensing,2013,7(1):32-45.
[5] ENDLIEH R M,WOLF D E,HALL D L,et a1.Use of a pattern recognition technique for determining cloud motions from Sequences of Satellite photographs[J].Journal of Applied Meteorology,1971,10(2):105-117.
[6] THOMASM H,THOMASM N.A short-term cloud forecasts scheme using cross correlation[J].Weather and Forecasting,1993,8(4):401-411.
[7] LIU H,TIANA H Q,PANA D,et al.Forecasting models for wind speed using wavelet,wavelet packet,time series and Artificial Neural Networks[J].Applied Energy,2013,107(C):191-208.
[8] MALIK M H,ARIF A F.ANN prediction model for composite plates against low velocity impact loads using finite element analysis[J].Composite Structures,2013,101(2013):290-300.
[9] BOX G,JENKINS G M.Time series analysis:forecasting and control[M].Beijing:China Statistics Press,1997:101-135.
[10] HAN Q Y,ROSSOW W B,LACIS A A.Near-global survey of effective cloud droplet radii in liquid water clouds using ISCCP data[J].Journal of Climate,1994,7(1):465-497.
[11] HAN Q,ROSSOW W B,CHOU J,et al.Global variation of droplet column concentration in low-level clouds[J].Geophysical Research Letters,1998,25(9):1419-1422.
[12] JONATHAN D C,CHAN K S.Time series analysis with applications in R[M].2nd ed.Beijing:China Machine Press,2011:137-152.

