带干扰的相依双险种再保险模型的破产概率

蒋兰青

(闽江师范高等专科学校，福建 福州 350108)

对单一的成数或超额赔款再保险模型的破产概率的研究已取得很多成果，然而随着人们保险意识的增强和保险业的不断发展，险种逐渐呈现多元化，且同一险种引起的索赔也可能不再是单一的.文献[1]研究了一类理赔具有某种相依关系的超额赔款再保险;文献[2]建立了成数与超额赔款混合双险种风险模型，得到了两险种的最优自留水平.本文在文献[2]给出的模型基础上，将文献[1]中的相依关系引入该模型中，建立了一类更为一般的再保险模型，在按期望值原理计算保费下，得到了改进模型的Lundberg不等式和最终破产概率.

1 预备知识与模型建立

定义1[3]计数过程{N(t),t≥0}称为参数为λ(λ>0)的齐次Poisson过程，如果：

(1)N(0)=0；

(2)过程有独立增量；

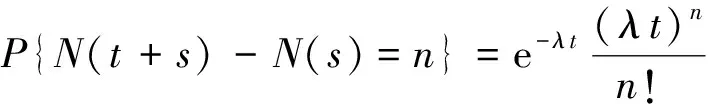
定理1[4](齐次Poisson过程的可加性)设M={Mt,t≥0}和N={Nt,t≥0}是强度分别为λ1和λ2的齐次Poisson过程，并且两个过程相互独立.对于每一个ω∈Ω和任意的t≥0，令

Kt(ω)=Mt(ω)+Nt(ω),

则上式定义的过程K={Kt,t≥0}称为过程M={Mt,t≥0}和N={Nt,t≥0}的叠加，且为服从强度为λ=λ1+λ2的齐次Poisson过程.

定理2[4]设{S(t),t≥0}是一个复合Poisson过程，Poisson过程{N(t),t≥0}的强度为λ，则:

(1)S(t)有独立增量；

下面将讨论模型的建立过程.定义完备概率空间(Ω,F,P)，本文考虑的所有随机变量都是定义在该概率空间上的.首先建立如下的未考虑再保险的相依双险种风险模型，盈余过程{U(t),t≥0}满足：

(1)

其中：

(1)u≥0为保险公司的初始资金，P为单位时间的保费率；

(2){Xi,i≥1}和{Yj,j≥1}是取值于[0,∞)上的非负独立同分布的随机变量序列，分别表示险种1在第i次的理赔额和险种2在第j次的理赔额，设其分布函数分别为F(x)和G(y)，均值分别为μ1和μ2，且对x≤0和y≤0分别有F(x)=0，G(y)=0；

(3)N1(t),N2(t)分别表示两类险种在t时间内的理赔次数,且N1(t)与N2(t)之间相互独立.显然可以找到相互独立的参数分别为λ1,λ2,λ的Poisson分布K1(t),K2(t),K(t),使得N1(t)=K1(t)+K(t)，N2(t)=K2(t)+K(t)成立.这样两险种的各自理赔总额N1(t)与N2(t)便通过K(t)联系起来.由定理1易知N1(t)与N2(t)是分别服从强度为λ1+λ，λ2+λ的齐次Poisson过程.

(4){W(t),t≥0}为标准维纳过程，表示保险公司不确定的收益和支出，σ>0为干扰因子，且假设{Xi,i≥1}，{Yj,j≥1}，{N1(t),t≥0}，{N2(t),t≥0}，{W(t),t≥0}之间相互独立.

现假设保险公司对两类险种采取不同的再保险策略，即对险种1的理赔选择自留比例为a的成数再保险，对险种2的理赔选择自留额为M的超额赔款再保险，则保险公司的盈余过程与盈利过程分别为：

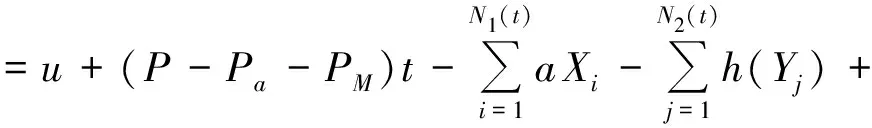
(2)

S(t,a,M)=U(t,a,M)-u,t≥0,

(3)

其中h(Yj)=min {Yj,M}表示险种2在第j次的理赔额，Pa和PM分别为成数再保险和超额赔款再保险的单位时间再保费率.假设原保险公司与再保险公司都是按期望值原理收取保费，且原保险、成数再保险和超额赔款再保险的安全负载分别为θ，θ1，θ2(θ≤θ1,θ≤θ2)，则P=(1+θ)[(λ1+λ)μ1+(λ2+λ)μ2]，Pa=(1+θ1)(1-a)(λ1+λ)μ1，PM=(1+θ2)(λ2+λ)E[(Yj-M)+].

定义3记Ta,M=inf {t|U(t,a,M)<0}为保险公司的破产时刻，若对所有t均有U(t,a,M)>0，则Ta,M=∞； 记ψ(u,a,M)=P(Ta,M<∞|U(0)=u)，∀u≥0表示最终破产概率.

引理1[1]盈利过程{S(t,a,M),t≥0}是一个右连续的随机过程，具有如下性质：

(1)E[S(t,a,M)]=[P-Pa-PM-(λ1+λ)E(aX)-(λ2+λ)E(h(Y))]t>0；

(2)具有平稳独立增量性；

(3)存在正数r，使得E[e-r S(t,a,M)]<+∞.

引理2对于盈利过程{S(t,a,M),t≥0}，存在函数ga,M(r)使得E[e-r S(t,a,M)]=et ga,M(r)，其中

ga,M(r)=(Pa+PM-P)r+(λ1+λ)(MX(ar)-1)+

(4)

上式中MX(r)，Mh(Y)(r)分别是X,h(Y)的矩母函数.

证明总的自留理赔额的矩母函数为

E{[MX(ar)]N1[Mh(Y)(r)]N2}=E{[MX(ar)]K1[Mh(Y)(r)]K2[MX(ar)Mh(Y)(r)]K}=

E[MX(ar)]K1·E[Mh(Y)(r)]K2·E[MX(ar)Mh(Y)(r)]K=

exp{t[(λ1+λ)(MX(ar)-1)+(λ2+λ)(Mh(Y)(r)-1)+λ(MX(ar)-1)(Mh(Y)(r)-1)]}，

令E[S(a,M)]为再保险后，保险人每单位时间的期望净利润，即E[S(a,M)]=P-Pa-PM-(λ1+λ)E(aX)-(λ2+λ)E(h(Y)); 又令L={(a,M): 0≤a≤1,M≥0且E[S(a,M)]>0}.

引理3对任意的(a,M)∈L，方程ga,M(r)=0在r>0内有唯一的正解R=Ra,M，并称此解为调节系数.

λE(aXer aX)(Mh(Y)(r)-1)+λE(h(Y)er h(Y))(MX(ar)-1)+rσ2，

证明由引理1易知{U(t,a,M),t≥0}有独立平稳增量，又由文献[5]知当{U(t,a,M),t≥0}有独立平稳增量时，M(t,a,M)为鞅的充要条件是E[e-Ra,MU(t,a,M)]=e-Ra,Mu.由引理2和引理3知，存在函数ga,M(r)使得E[e-Ra,MS(t,a,M)]=et ga,M(Ra,M)=1，故有E[e-Ra,MU(t,a,M)]=E[e-Ra,Mu]E[e-Ra,MS(t,a,M)]=e-Ra,Mu.证毕.

2 Lundberg不等式与最终破产概率

定理3对盈余过程{U(t,a,M),t≥0}，最终破产概率满足下面的Lundberg不等式

ψ(u,a,M)≤e-Ra,Mu,

(5)

其中Ra,M为调节系数.

证明根据Doob’s不等式[6]及引理1—3有

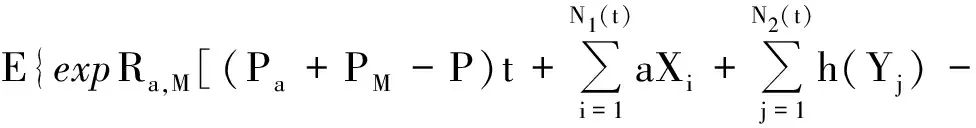
e-Ra,Mu·E[e-Ra,MS(t,a,M)]=e-Ra,Mu.

令t→∞，则有

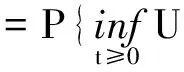
证毕.

定理4对于本文建立的模型(1)，其最终破产概率为

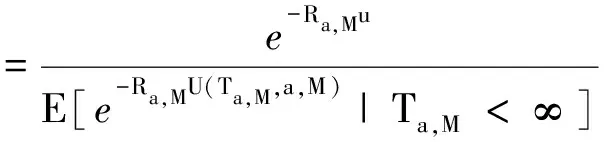
(6)

其中Ra,M为调节系数.

e-Ra,Mu=E[M(t0∧Ta,M)|Ta,M≤t0]P(Ta,M≤t0)+E[M(t0∧Ta,M)|Ta,M>t0]P(Ta,M>t0)=

E[M(Ta,M)|Ta,M≤t0]P(Ta,M≤t0)+E[M(t0)|Ta,M>t0]P(Ta,M>t0).

(7)

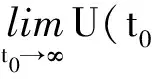
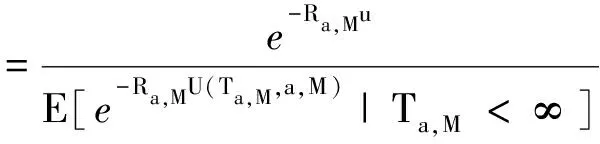
由于对破产时刻Ta,M有U(Ta,M,a,M)<0，于是e-Ra,MU(Ta,M,a,M)>1，从而由(6)式得风险模型(1)的破产概率ψ(u,a,M)≤e-Ra,Mu，亦可得定理3中(5)式的结果.

参考文献：

[1]CentenoM L. Dependent risks and excess of loss reinsurance[J]. Insurance: Mathematics and Economics,2005,37:229-238.

[2]蔡平霞.双险种最优再保险策略[J].数学理论与应用,2010,30(2):101-104.

[3]Grandell J. Aspects of Risk Theory[M]. New York: Springer-Verlag,1991.

[4]殷小琴.复合泊松过程及其在保险风险中若干应用[J].数学理论与应用,2009,29(4):122-124.

[5]Gerber H U,Shiu E. On the time value of ruin[J]. North Amer Actuar J,1998,2:48-78.

[6]Øksendal B. Stochastic Differential Equations[M]. New York: Springer-Verlag,2000.