基于工作变形分析的镗杆设计研究*

袁 黎，胡忠举，梁红强，彭 威，朱萍玉

(1.湖南科技大学 机电工程学院，湖南 湘潭 411201； 2.广州大学 机械与电气工程学院，广东 广州 510006)

基于工作变形分析的镗杆设计研究*

袁 黎1，胡忠举1，梁红强1，彭 威1，朱萍玉2

(1.湖南科技大学 机电工程学院，湖南 湘潭 411201； 2.广州大学 机械与电气工程学院，广东 广州 510006)

基于振动方程，采用传递矩阵法和模态叠加法，推导了镗杆的工作变形公式；应用算例对该工作变形公式进行了验证。选取普通镗杆和阻尼镗杆作为研究对象，采用该工作变形公式快速分析两种镗杆的工作振型、模态贡献量和频响曲线，进行对比分析，指导镗杆的结构设计。结果表明该工作变形分析作为快速分析镗杆工作振动特性的新方法，为镗杆结构参数设计计算提供了新的参考依据。

工作变形；镗杆；模态贡献量；频响曲线

0 引 言

工作变形(Operational Deflection Shape， ODS)分析是一种新的结构振动分析方法，它区别于模态振型分析。模态是结构的固有属性，而ODS指结构在某一工况或特定频率下的受迫响应，随结构载荷的变化而变化[1-4]。工程实际中，ODS可用于对某阶模态振型作用溯源，识别在工作变形中的贡献大小，进而为结构设计做指导。笔者针对有限元法仿真分析计算量较大，分析时间长，对计算机配置要求较高的问题，拟采用一种新方法对设计前后的镗杆进行振动特性研究，可快速得到镗杆的工作振型、模态贡献量和频响曲线等振动特性参数，通过这些参数对比，即可指导镗杆的结构设计。

1 镗杆工作变形函数推导

镗杆可视为有限自由度系统。将其离散成N个质点系，质点系间通过刚架结构元连接。根据传递矩阵法，质点矢量位移在这些质点之间传递[5-7]。连续镗杆系统便转化为由多个连接元组成的N自由度系统，如图1所示。

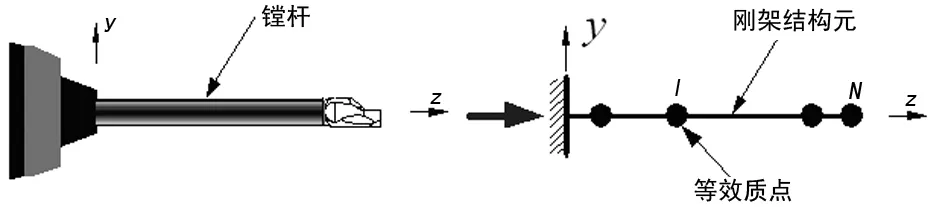
图1 镗杆等效形式

忽略阻尼的影响,此N自由度系统振动方程为：

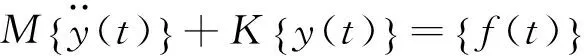
(1)

质量阵和刚度阵为：

(2)

式中：mij为质量阵中的元素；kij为刚度阵中的元素。

其模态频率和模态振型通过式(3)计算:

(3)

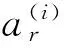
设镗杆可视为线性时不变系统，则离散镗杆系统任一点l处某时刻的响应可表示为该刚架结构元各阶模态的线性叠加[8]：

(4)

式中：l为被测点；r为模态阶次；φlr为被测点l处的振型系数；qr(ω)为比例因子；Mr为模态质量；Kr为模态刚度。

综合式(2)～(4)，得镗杆的工作变形函数：

(5)

2 算 例

设简易镗杆的横截面形状及尺寸如图2所示。弹性模量为200 GPa，泊松比为0.3，密度为7 850 kg/m3，悬伸长度为225 mm。将镗杆离散成9段，如图3所示。

图2 镗杆横截面 图3 镗杆离散示意图

通过有限元仿真分析，可得到镗杆在任意频率下的工作振型[9]，分别取频率为500 Hz、1 000 Hz、2 000 Hz、3 000 Hz时镗杆的工作振型，如图4所示。通过镗杆的工作变形函数得到对应的4个频率下的工作振型如图5所示。

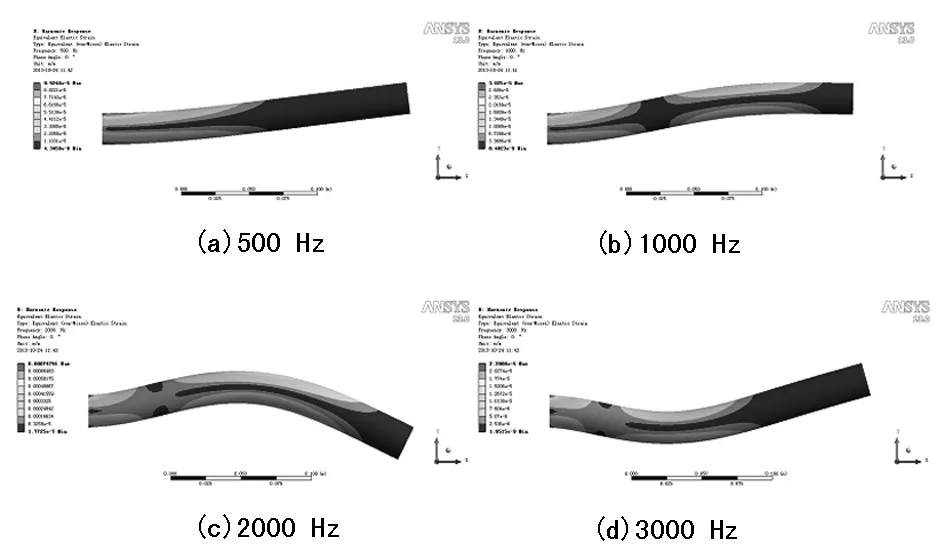
图4 有限元仿真结果

图5 工作变形公式计算结果

由图4、5的对比验证可知，通过工作变形函数得到的工作振型与仿真分析结果基本一致，即采用工作变形函数可正确地描绘出镗杆的工作振型，且计算量小，对计算机配置要求很低，使用方便快捷。

3 应用研究

选取普通镗杆和阻尼镗杆作为研究对象，如图6所示，两种镗杆的长径比相同，刀杆部分的形状和长度也相同，阻尼镗杆则是对普通镗杆的头部结构形状进行了优化。

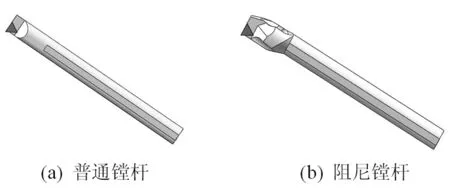
图6 研究对象

采用工作变形函数可对这两种镗杆进行工作模态分析，任意选取三个工作频率：800 Hz、1 700 Hz、2 600 Hz，即可得到该阻尼镗杆在这三个工作频率下的工作振型，如图7所示。

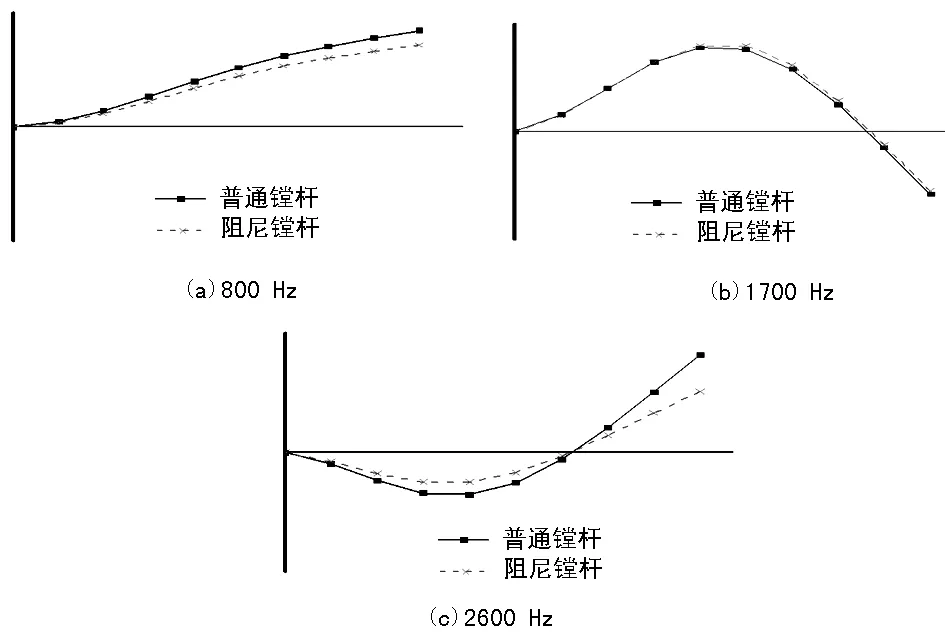
图7 工作振型对比

实线是普通镗杆的工作振型，虚线是阻尼镗杆的工作振型。由图7可知，这两种镗杆在任意频率下的工作振型相似，但是普通镗杆的刀头部分的振动幅度明显较大，即阻尼镗杆的抗振能力更强。

通过模态判定准则可分析各阶模态对工作变形的贡献量[10]。假定{x}和{y}为两个长度相等的向量，模态判定准则MACxy为：

(6)

经计算，两种镗杆各阶模态在800 Hz、1 700 Hz和2 600 Hz处ODS的贡献量如表1、2所列。

表1 普通镗杆模态贡献量

表2 阻尼镗杆模态贡献量

由表1、2可知，工作频率在800 Hz时，第1阶固有模态对两种镗杆的振动贡献均较大；工作频率在1 700 Hz时，第2阶固有模态对两种镗杆的振动贡献均较大；工作频率在2 600 Hz时，第1、2、3阶固有模态对普通镗杆的振动贡献较大，第1、2阶固有模态对阻尼镗杆的振动贡献较大。通过识别镗杆固有模态在工作变形中的贡献量，得到极易引起镗杆颤振的模态固有频率。

采用工作变形函数获得两种镗杆刀头端的频率响应曲线进行对比，如图8所示，0～2100 Hz范围内，阻尼镗杆与普通镗杆的频率响应曲线大部分吻合，即在该频率范围内，阻尼镗杆未体现出较好的动态减振性能；但在2 100～4 700 Hz范围内，阻尼镗杆的频率响应曲线明显高于普通镗杆的，即在该频率范围内，阻尼镗杆具备较好的动态减振性能。

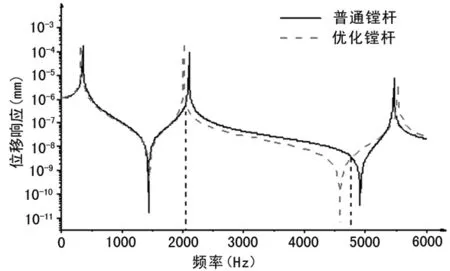
图8 频响曲线对比

4 结 语

推导了一种新的工作变形函数，并采用算例对比验证了该工作变形函数的正确性；以普通镗杆和阻尼镗杆作为研究对象，采用该工作变形函数对比研究了两种镗杆的工作振型、模态贡献量和频率响应曲线等动态特性，得到了阻尼镗杆适用的频率范围，验证了阻尼镗杆的减振性能。

[1] Devriendt C, Steenackers G, DE S G, et al. From Operating Deflection Shapes Towards Mode Shapes Using Transmissibility Measurements[J]. Mechanical Systems and Signal Processing, 2010,24(3):665-677.

[2] Wonki B, Yongsoo K, Jedol D, et al. Scaling the Operating Deflection Shapes Obtained from Scanning Laser Doppler Vibrometer[J]. Journal of Nondestructive Evaluation,2011,30(2):91-98.

[3] 陈永会，李志谭，李海虹.基于ODS测试方法的钻架模型试验模态分析研究[J].太原科技大学学报，2005，26(4)：268-272.

[4] 程 珩，赵 远.工作模态分析在减速器监测和诊断中的应用 [J]. 振动、测试与诊断，2010，30(2)：197-200.

[5] 兰贤辉，李育锡，苏武会.轮转子系统稳态不平衡响应分析的整体传递矩阵法[J]. 机械科学与技术，2009，28(12)：1613-1615，1620.

[6] 彭泽军，杨兆建.多支承转子轴承系统的负荷敏感度研究[J].工程设计学报，2002，9(1)：12-16.

[7] Rui X T, Edwin K, Bao R, et al. Discrete Time Transfer Matrix Method for Dynamics of Multibody System with Flexible Beams Moving in Space[J].Acta Mechanica Sinica, 2012, 28(2):490-504.

[8] 傅志方，华宏星.模态分析理论与应用[M].上海:上海交通大学出版社，2000.

[9] 孙广敏，安丰柱.基于ANSYS Workbench对立式车床横梁的模态分析[J].机械研究与应用，2013(4)：40-41，46.

[10] 郭 荣，周 鋐.某型轿车白车身实验模态分析及动态特性评价[J].机械设计，2010(8)：18-22.

Design Research of Boring Bar Based on ODS Analysis

YUAN Li1, HU Zhong-ju1, LIANG Hong-qiang1, PENG Wei1, ZHU Ping-yu2

(1.CollegeofElectromechanicalEngineering,HunanUniversityofScienceandTechnology,XiangtanHunan411201,China;(2.SchoolofMechanicalandElectricEngineering,GuangzhouUniversity,GuangzhouGuangdong510006,China)

Based on vibration equation, a ODS formula of boring bar was deduced with transfer matrix method and mode superposition method. An example was used to verify the accuracy of this method. A general boring bar and a damping boring bar were selected as objects of study. The ODS, modal contribution and frequency response curve of this two kinds of boring bar were researched rapidly with this method. Comparisons of the results were used to direct structural design of boring bar. The results show that ODS analysis based on this ODS formula is a new method to analyze operational vibration characteristic of boring bar rapidly. It provides a new reference basis for structure parameter design calculation of boring bar.

ODS; boring bar; modal contribution; frequency response curven

2014-01-24

国家自然科学基金资助项目(编号：51105140)；湖南科技大学研究生创新基金项目(编号：S120016)

袁 黎(1987-)，男，湖南郴州人，在读硕士，主要从事先进制造工艺与装备研究方面的工作.

TH113.1

A

1007-4414(2014)02-0017-03